基于子空间加权的多重信号分类时延估计算法

卢 俊， 张群飞，史文涛，张玲玲

(西北工业大学航海学院，陕西 西安 710072)

0 引言

水下探测通信一体化将独立的水下探测与水声通信系统集成在一起，单节点水下探测通信一体化利用通信发射信号作为共享信号，实现目标主动探测与信息传输功能[1]。一体化系统采用收发分置方式，信号的收发是同时的，接收端在接收有效信号的同时不可避免地接收到本机的发射泄漏干扰以及多径反射等干扰信号，为保证系统的探测与通信性能，需对干扰进行抑制。

传统的干扰抑制方法可以分为被动与主动两种方式[2]。被动干扰抑制性能往往受限于系统物理结构，而主动干扰抑制不受物理结构限制，因此应用较为广泛。常见的主动干扰抑制技术利用参考信号，通过延迟器、衰减器、移相器等重建干扰信号[3-5]，当参考信号与接收干扰信号相对时延估计存在误差时，重建的干扰信号将存在偏差，导致干扰抑制性能下降，因此对接收干扰信号相对于参考信号的时延进行精确估计以及分辨是保证干扰抑制性能的关键。

互相关法是经典的时延估计方法，其要求信号与噪声、噪声与噪声互不相关，对非平稳信号和可变时延估计误差较大。针对该缺陷，Knapp和Carter提出了广义加权互相关时延估计算法(GCC)[6]，其本质是对接收信号进行预白化处理，该方法需要信号与噪声的先验知识。为了克服GCC需要先验知识的不足，文献[7]提出了一种基于最小均方误差(LMS)的自适应时延估计方法；文献[8]提出一种基于小波变换和递归最小二乘(RLS)的自适应时延估计算法。在多径情况下，为了获取时延分辨率和估计精度；文献[9] 提出低信噪比宽带信号的高精度时延估计算法，该算法的精度不受采样间隔的限制，能适应较低的信噪比；文献[10]提出了基于稀疏信号重构的超分辨时延估计算法；文献[11]将时延估计表示为一个稀疏信号重构问题，提出利用网格外压缩感知进行时延估计。利用阵列信号处理中波达方向(DOA)估计与时延估计的联系，Buckstein和Kailath将MUSIC算法应用到时延估计中[12]。文献[13]结合正弦信号频率估计模型，通过数据相关构造协方差矩阵，采用多重信号分类(MUSIC)算法进行时延估计。文献[14]对信号进行平滑处理构造协方差矩阵，然后对子空间特征结构进行加权获取更高的时延估计精度与分辨率。对于窄带信号MUSIC时延估计分辨率下降问题，文献[15]提出了一种新的对角加载最小二乘MUSIC算法。针对水下探测通信一体化干扰抑制中时延估计误差对主动干扰抑制性能影响，以及常规MUSIC时延估计方法因数据长度有限、信噪比低使得信号与噪声子空间不完全正交，而导致时延估计性能下降这一问题，提出了基于子空间加权的多重信号分类时延估计方法。

1 基于MUSIC的时延估计模型

1.1 时延估计误差对主动干扰抑制影响

多抽头延迟滤波是一种常见的主动干扰抑制方法，其结构如图1所示。干扰抑制链路通过调节时延、相位、幅度逼近干扰链路中的时延、相位以及幅度，重建干扰信号。当时延、相位及幅度估计存在误差时，导致重建的干扰信号存在偏差，从而影响抑制效果。

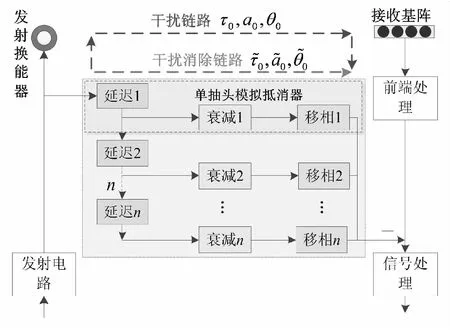
图1 多抽头延迟滤波器自干扰抵消示意图Fig.1 Schematic of self-interference cancellation by multi-tap delay filters

假设发射信号为s(t)ejωct，其中s(t)为基带信号，ωc为载波角频率，即信号功率P0为：

P0=E{|s(t)ejωct|2}=E{|s(t)|2}

(1)

发射信号经过信道传输后，存在延时τ0以及a0倍的幅度衰减，即接收端信号为：

r0(t)=a0·s(t-τ0)·ejωc(t-τ0)

(2)

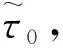
(3)

(4)

(5)

式(5)中，SP(f)为s(t)的功率谱密度函数，B为信号带宽，即有：

(6)

单节点水下探测通信一体化系统以发射的通信信号作为共享信号实现目标探测与信息传输，常用的水声通信调制信号有频移键控(FSK)、相移键控(PSK)以及最小频移键控(MSK)等调制信号[16-17]。分析时延误差对BPSK调制信号、MSK调制信号以及功率谱为三角分布的三种信号的干扰抑制性能的影响。假设信号功率P0=0 dB，带宽B分别为3、5、7 kHz，信号幅度a0=1(考虑无衰减)，信号持续时间Ts=0.1 s时，考虑上述三种信号，得到时延误差、信号带宽与干扰抑制性能关系如图2所示。

图2 不同功率谱密度信号、带宽、时延误差干扰抑制性能影响分析Fig.2 Analysis on suppression performance of different power spectral density signals, bandwidth and time delay

由图2可知，干扰抑制性能与信号功率谱密度分布有关，且残余干扰功率随着时延误差、带宽的增加而增加，时延估计误差增加到一定程度时，残余干扰功率趋于恒定值。当干扰信号类型确定后，为了增加干扰抑制能力，应尽量减小信号带宽与时延估计误差，实际应用中信号带宽往往是固定的，因此减小延时估计误差是有效的途径。

1.2 MUSIC时延估计模型

传统的互相关时延估计方法性能受限于信号带宽，且当接收信号中两干扰时延间隔小于发射信号的相关时间时，时延估计性能将下降[17]。将时延估计转换为频率估计问题，并将DOA估计中的MUSIC算法应用到时延估计中，获取高分辨以及高精度的时延估计。对于一体化系统，发射的共享信号s(t)精确已知，经信道传输，接收端接收到的发射泄漏干扰信号为：

(7)

式(7)中，L为发射泄漏干扰信号多径反射条数，w(t)为零均值高斯白噪声，Tr为干扰信号持续时间，式(7)离散化可表示为：

(8)

将参考信号与接收的发射泄漏干扰信号补零到长度为Ka=Kr+Ks-1，Kr与Ks分别为接收的发射泄漏干扰信号与参考信号长度，然后将两者做圆周卷积，即有：

(9)

参考信号s(n-m)用离散傅里叶逆变换形式表示：

(10)

式(10)中，S(k)为s(n)的离散傅里叶变换(DFT)形式，将式(8)与式(10)带入式(9)中即有：

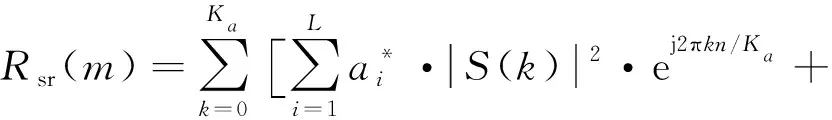
(11)

式(11)中，Wr(k)=S(k)W*(k)，W(k)=DFT(w(k))。

假设Rsr(m)=DFT[r(k)]，将式(11)进行IDFT即有：

(12)

将式(12)表示成向量形式：

(13)

式(13)中，

均匀线列阵(ULA)结构下的经典阵列信号处理接收模型中，信号的角度参数、时延参数是密切相关的，估计模型具有内在一致性，因此阵列信号处理的方法可以应用到时延估计中。

2 基于子空间加权的MUSIC时延估计

2.1 常规MUSIC时延估计方法

MUSIC算法对接收数据的协方差矩阵进行特征值分解，得到与信号分量相对应的信号子空间以及与信号分量相正交的噪声子空间，然后利用这两个子空间的正交性来估计信号参数。将MUSIC算法应用到时延估计中，利用接收的发射泄漏干扰信号与参考信号圆周卷积的IDFT变化序列r(k)构造协方差矩阵为:

(14)

(15)

式(15)中，i=0,1,…,Ka-M，据r(i)构建接收数据的协方差矩阵Rs为：

(16)

(17)

在实际应用中，对参数的估计是通过最小优化搜索实现的，根据式(13)即有

(18)

由式(18)可得MUSIC算法的时延估计谱表达式为：

(19)

式(19)表示对时延谱进行谱峰搜索，得到L个最大值点对应的时间τ即为干扰对应的时延值。

2.2 基于子空间加权的MUSIC时延估计方法

理想条件下Us与Un相互正交，实际中由于数据长度有限、信噪比较低，信号子空间与噪声子空间并不完全正交，特征值存在偏差，算法估计性能下降。利用式(16)构造接收数据的协方差矩阵Rs，并进行特征值分解，同时对噪声特征值进行修正，修正的噪声特征值为：

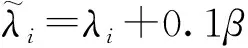
(20)

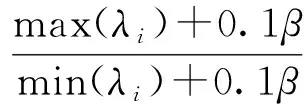
(21)

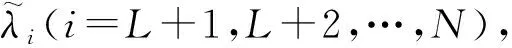
(22)

(23)

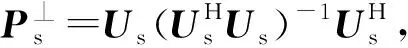
(24)

同时，式(17)可表示为：

(25)

即有信号子空间与特征值重构的信号协方差矩阵为：

(26)

(27)

由式(24)，时延导向矢量在信号子空间上的投影值TRS较大，非正确时延导向矢量投影值TNS较小，为利用信号子空间信息，将式(24)与式(27)代入式(23)中，即有修正后的时延估计表达式为：

(28)

从利用信号子空间信息看，利用时延导向矢量Λ(τ)S投影到信号子空间上的投影值Ts，加权后算法的谱峰与传统MUSIC时延估计算法谱峰比为TRS/TNS>1，即对旁瓣具有一定抑制作用。且通过对传统MUSIC时延估计中噪声子空间的重构，以及对子空间进行加权处理，较传统MUSIC时延估计算法具有更好的估计性能。

3 仿真实验

采用BPSK调制信号作为水下探测通信一体化的发射共享信号进行仿真实验，信号频带为4～8 kHz，载频为fc=6 kHz，采样频率fs=48 kHz，延迟以采样间隔为基准(单位为1/fs，fs为采样频率)。

3.1 估计精度

随机产生一个整数作为延迟的点数，在不同信噪比情况下比较所提传统互相关法、常规MUSIC算法、文献[14]所提的SSMUSIC算法以及所提加权MUSIC算法的时延估计精度，仿真结果如图3所示。

图3 时延估计精度比较Fig.3 Comparison of time delay estimation accuracy

从仿真结果可以看出，常规MUSIC方法、SSMUSIC方法以及所提方法估计精度在低信噪比情况优于互相关法，且所提方法好于常规MUSIC方法，与SSMUSIC方法相近。

3.2 时延分辨

在1～10内随机产生两个整数作为延迟的点数，并产生对应的两条延迟干扰信号，然后合成为接收发射泄漏干扰信号。为验证所提加权MUSIC算法的时延估计性能，分别在不同信噪比、数据长度情况下，与常规MUSIC算法以及SSMUSIC算法进行对比。

3.2.1信噪比与时延估计性能关系

采用上述所提的BPSK调制共享信号，分别在信噪比为SNR=-8∶1∶4 dB情况下进行仿真，得到如图4所示的仿真结果。

图4 时延估计性能随信噪比变化关系Fig.4 Relationship between performance of delay estimation and SNR

从图4可知，三种MUSIC算法估计性能随着信噪比的增加而提高，但所提方法均方误差与分辨概率均优于常规MUSIC算法与SSMUSIC算法。

3.2.2数据长度与时延估计精度关系

采用上述所提的BPSK调制共享信号，在信噪比为0 dB的情况下，分别采用数据长度为20∶20∶200采样点进行仿真，得到如图5所示的仿真结果。

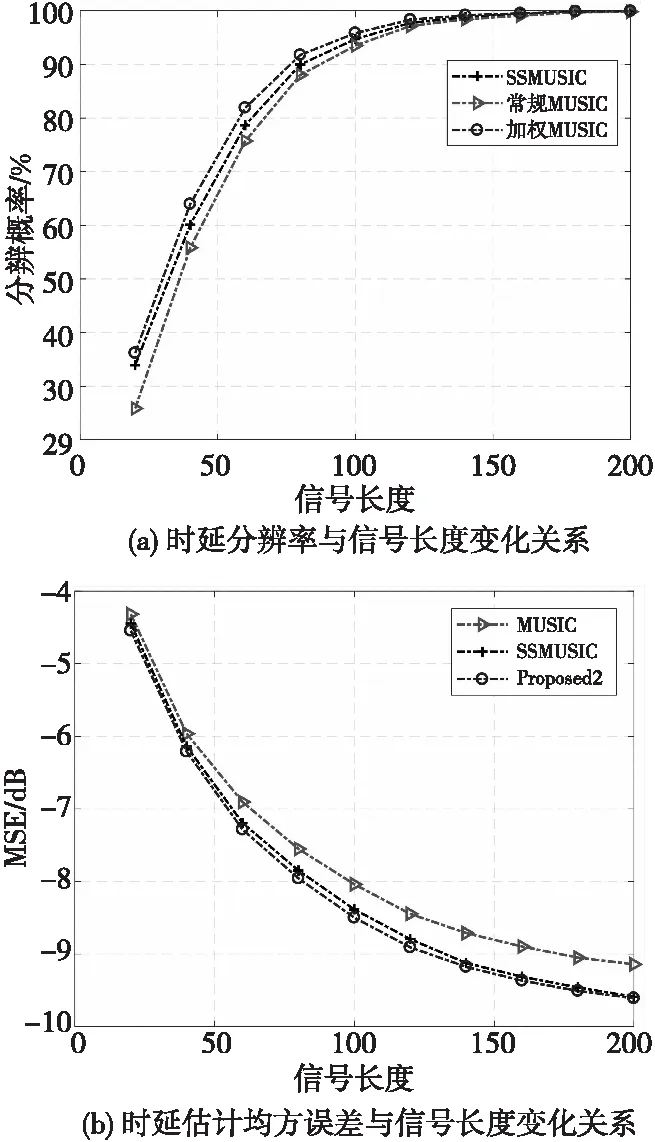
图5 时延估计性能随信号长度变化关系Fig.5 Relationship between performance of delay estimation and the length of the signal

从图5可知，三种MUSIC算法估计性能随着信号长度的增加而提高，但所提方法均方误差与分辨概率均优于常规MUSIC算法与SSMUSIC算法。

综上所述，所提方法的估计精度优于传统互相关法、MUSIC时延估计算法与SSMUSIC算法。随着信噪比的提高或数据长度的增加，均方误差并未收敛到零处，这是由于信号数据长度有限或信噪比因素导致特征值分解后的子空间并未完全正交，存在误差，从而使得估计误差收敛于一个较小的值。通过对时延谱的修正，所提方法较常规MUSIC算法以及SSMUSIC算法在不同信噪比和数据长度对多条干扰均具有更好的时延分辨率与较低的估计误差。

4 结论

本文提出了一种基于子空间加权的多重信号分类时延估计方法。该方法通过重构噪声子空间，并利用信号特征值与噪声功率构造加权值，对子空间进行加权，实现对MUSIC时延估计谱的修正。所提方法一定程度上解决了常规MUSIC时延估计方法因数据长度有限、信噪比低等情况使得噪声与信号子空间不完全正，导致时延估计性能下降的问题。仿真结果表明所提方法较互相关法、MUSIC算法和SSMUSIC算法具有更高的时延估计精度，以及更优的时延分辨率。