舰艇随船备件需求量的数学模型研究

敬 军

（中国舰船研究设计中心，湖北 武汉，430064）

0 引言

在舰艇的保障工作中，备品备件供应是保障工作的主要内容之一，它不仅直接影响到故障装备的及时修复，也是保障工作中经费投入最大的工作，有时达到寿命周期内所有使用与维修保障经费的一半左右。如果不能科学合理地确定备品备件的品种与数量，将对装备的战备完好产生非常大的影响。舰艇出海时，备件不足会影响任务的完成，而备件数量过多，不仅会增加部队保养的工作量和经费的浪费，而且对于一些特殊的航行器，例如本身空间狭小的潜艇，会带来严重的负面影响。因此，舰艇备件量的精确确定对提高舰艇装备的战备完好率，控制舰艇的使用和维修成本具有重要意义。

近年来，许多学者在备件保障度模型、备件最优库层模型等诸多方面展开了较深入的研究[1-7]，并给出了一系列的预测备件需求量的数学模型。这些模型在计算时都需要大量的经验数据进行支撑，适用于成熟的装备。而对于新研的装备，特别是跟已有装备存在较大差别的，原有经验数据不能适用，其初始备件数量的计算结果往往偏离实际需要。据统计，有些新装备在部署部队初期，为了解决保障资源配套建设问题，同步确定了备品备件的品种与数量。但经过一段时间的使用过程后发现，尽管配发了大量的新装备器材，但使用的器材品种只占总品种的10%，而且还缺少10%的器材，在大量器材积压的情况下，并没有有效地解决好器材的保障问题。

本文在前人的工作基础上，分析现有的备件数量计算模型，针对舰艇随船备件需求，建立了基于经济性和任务成功性的备件需求量数学模型，给出了实例计算方法，对于装备备件数量的确定具有指导作用。

1 随船备件需求量计算模型

1.1 典型备件模型

备件可用概率是指一旦需用该备件时能取得它的概率，也称为备件满足率。备件数量与可用概率之间的关系可按非工作储备模型计算。非工作储备系统，有时也称为旁联系统，即组成系统的n个单元只有1个单元工作，其余处于待命状态。一旦工作单元发生故障，通过故障监测装置及转换装置接到另一个旁待的单元，使系统继续工作。非工作储备模型的可靠性框图如图1所示。

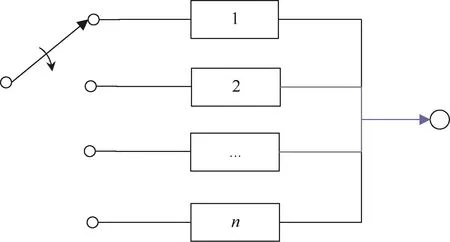
图1 非工作储备模型的可靠性框图Fig.1 Reliability block diagram of non-working reserve model

当所有单元相同，而且寿命服从指数分布，故障监测和转换装置的可靠度为 1时，系统任务成功的概率（系统可靠度）服从泊松过程。其数学模型为

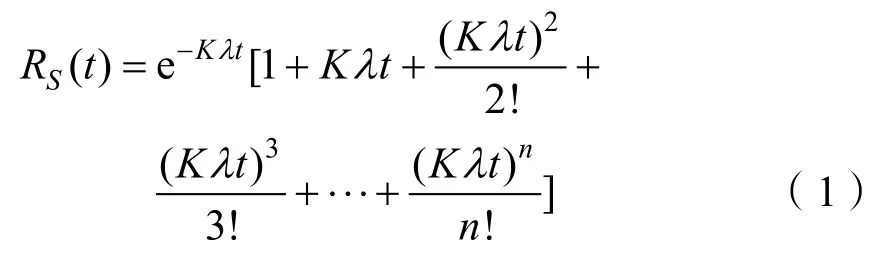
式中：n为系统非工作储备单元数；λ为每个单元的故障（失效）率；K为系统中相同工作单元数量（单机基数）。

如果把不工作的储备单元看作是备件，在工作单元有故障时都能通过换件予以排除，这样式（1）中的任务成功概率RS（t）就是备件可用概率P（S）。当系统中相同的单元有K个时，将式（1）中RS（t）表为备件可用概率P（S），并用累积泊松概率形式表达，则有：

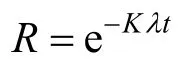
为了便于计算，可将式（2）做成累计泊松概率曲线，如图2，其纵坐标值可看成备件可用概率，横坐标值为Kλt，而以n标明的一组曲线，就是备件需求量。

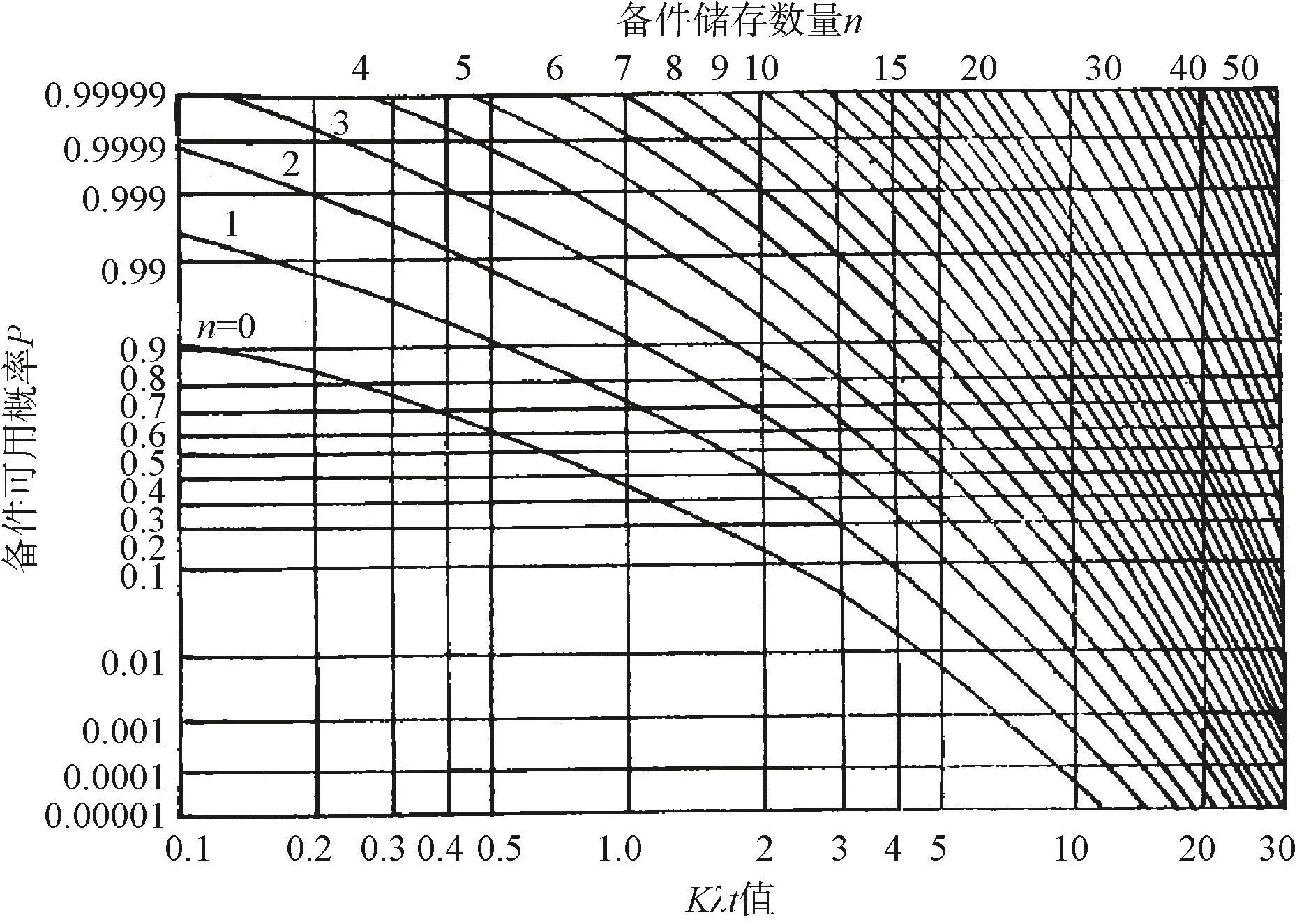
图2 泊松概率曲线Fig.2 Poisson probability curve

式（2）称为泊松备件模型，是最常用的备件模型。从式（2）可以看出，只有给出了备件可用概率，才能反推计算出备件需求量。对于研制阶段的舰艇来讲，由于缺乏实际使用的经验数据，即使借鉴已有装备的使用数据，也会因为装备之间的差异带来较大的问题，因此很难给出一个合理的备件可用概率，不能得到适当的备件需求量。

下文将从舰艇经济性和任务成功性的角度分别出发，建立备件可用概率的计算模型，和式（2）联合，即可确定备件需求量。

1.2 基于经济性原则的备件需求量计算模型

从经济性角度考虑，舰艇出海时要求保证在建立和保存备件上的花费是最小的。假定购买和保存一个备件的花费为c1，缺乏备件时的损失费用为c2，备件需求分布函数为F（n）。当储备M个备件时，如果备件需求量n≤M，即备件供应是充分的，则成本为（M－n）c1；如果备件需求量n＞M，即备件供应不足，则损失费用为（n-M）c2。

对于M个备件，建立备件期望费用方程为

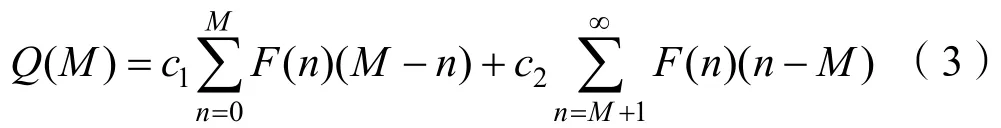
式中，假定备件需求分布函数F（n）满足泊松分布，则F（n）和备件可用概率P（S）满足下式关系

根据式（3）计算Q（S+1），有以下推导：

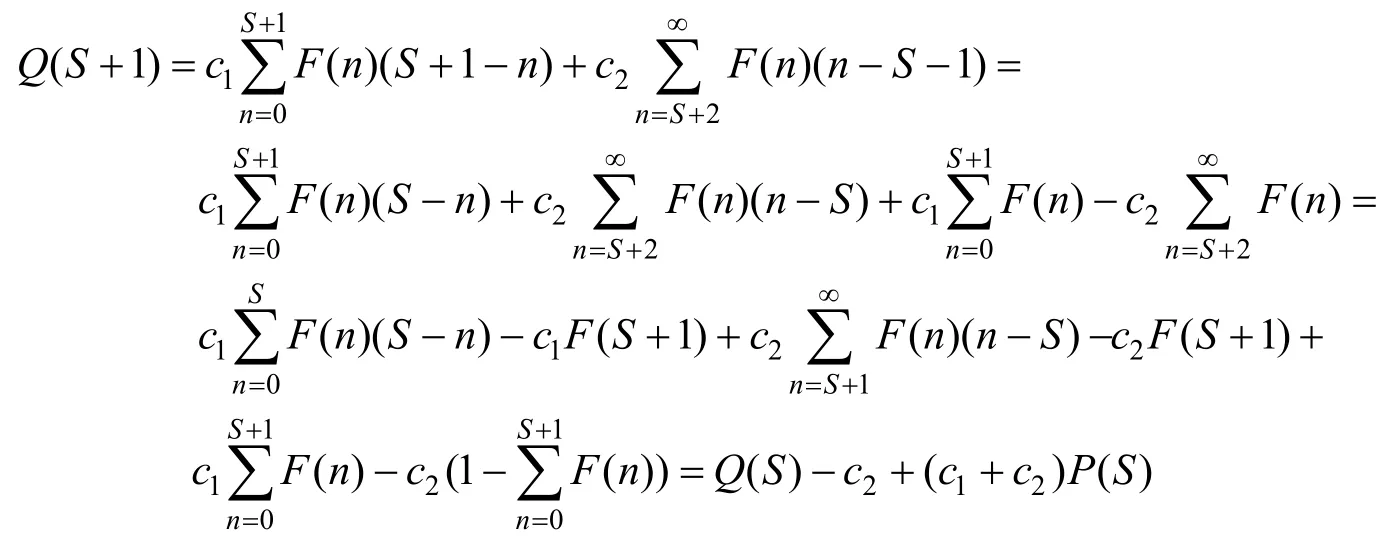
同理计算Q（S-1），可以得到：

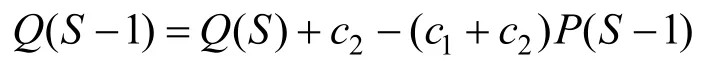
当备件处于最佳数量S0时，总费用Q（S0）最小，有：

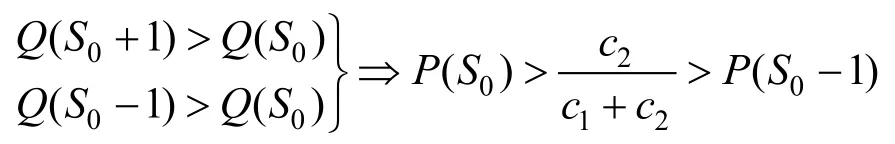
1.3 基于任务成功性的备件需求量计算模型

舰艇出海时，对于备件需求量的首要要求是能保证任务的成功性。因此对于一些不重要的、不涉及执行任务的设备可以按照经济性原则来确定备件数量，但对于关重件设备或涉及任务的设备，必须从保证任务成功的角度来确定备件数量。

由于备件采购和配置是间断进行的，在采购间隔期内，必须保证每次任务的成功，因此备件数量应该满足间隔期内成功执行k1次任务的需要。一般来讲，对于舰艇，备件采购间隔期可以按照1年确定，而执行任务次数k1如果不易确定，可以间隔期最大可能值代替。

而备件可用概率可以用任务可靠度Rm来替代。任务可靠度在研制阶段，通过可靠性建模、预计和分配，就已经分解到设备层面了，其分配、预计方法详见相关文献[8]，本文不加以冗述。

假定要求某舰艇执行一项使命任务的成功度不低于Rm0，该任务在备件采购或配置间隔期内执行k1次，则备件数量n应满足下式：

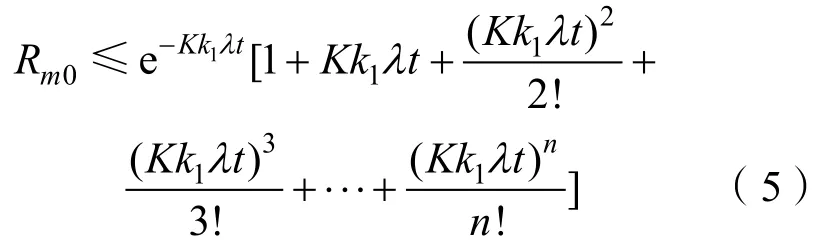
2 实例分析

已知某舰艇出海时间为30 d，执行某项任务时要求可靠度不低于0.80，该任务共有7个设备以串联关系参与，其中A设备的平均故障间隔时间（MTBF）是150 h，任务工作时间为20 h，备件成本为500元，损失费用为10 000元，试计算船上A设备的备件数量。

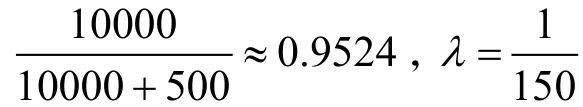
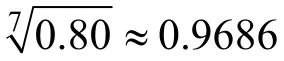
3 结束语

1）对于新研装备，由于缺乏大量使用数据，只能采用相似装备的经验数据，如果新研装备中存在较多新研设备或部件，则传统的备件需求量模型不再适用，应用本文的随船备件需求量模型则可以相对准确、合理地确定备件数量。

2）一般来讲，从经济性原则出发确定的可用概率比任务成功性得到的要低，因此基于任务成功性的备件数量通常比经济角度的备件数量多。因此对于空间比较狭小的新研装备，及不涉及任务的设备可以从经济性原则出发确定备件数量，在保证任务成功性的同时尽可能缩减备件数量。