基于地震动-磁场信息融合的舰船目标跟踪
马剑飞,颜 冰,李宾宾,王军锋
(1.海军工程大学 兵器工程学院,湖北 武汉430033;2.中国人民解放军 92916部队,海南 琼海 571400)
0 引言
舰船目标多为铁磁性材料构成,运动过程中会产生磁、地震动等多物理场信号[1],然而单一物理场所获取的目标特征信息有限,针对舰船目标磁信号的跟踪研究已经十分成熟[2-4],利用地震动物理场远程探测舰船的研究也比较广泛[5-7]。为提高对区域内目标的定位能力,本文通过多传感器地震动与磁场的信息融合,实现对目标的实时跟踪定位。
在多传感器探测阵列中,目标磁场模型选用经典的磁偶极子模型,目标地震动为三轴的振动信号,因而可以采用基于地震动信息的目标方位估计算法为跟踪滤波器提供方位信息,从而实现多传感器目标跟踪定位的信息融合。
1 磁-地震动模型
以目标中心建立坐标系,选用单一偶极子模型作为目标磁场模型。如图1所示,依据三轴加速度传感器接收目标地震动信号而建立的目标振动源信号投影模型[8-9]。其中坐标原点O是传感器的位置,投影模型的X,Y,Z三轴方向与传感器X,Y,Z三轴方向一致,在各向同性的均匀噪声场中存在目标振动源记为S。
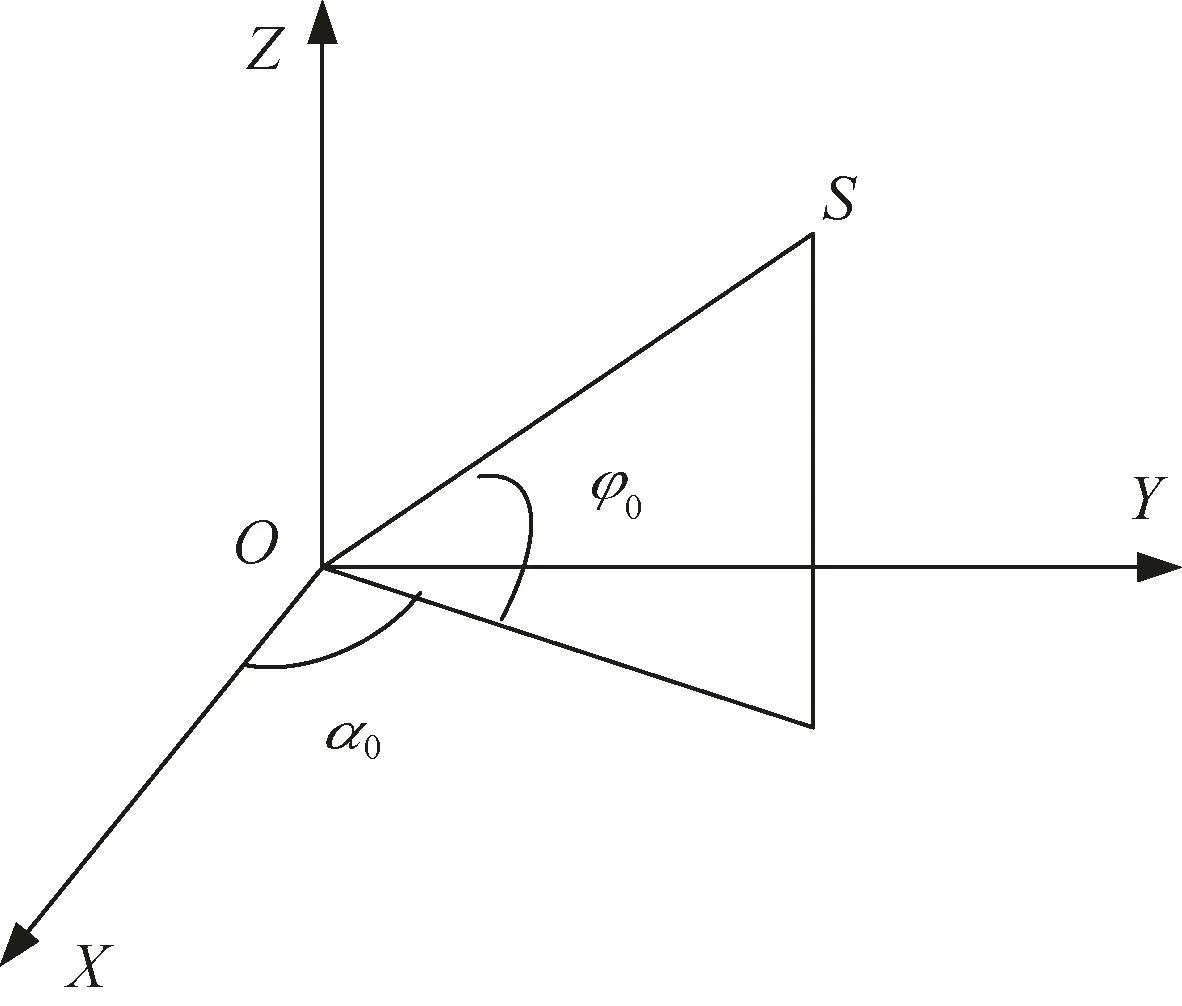
图1 三轴投影模型Fig.1 Triaxial projection model
假设目标振动源S位于u0方向,记方位向量u0为

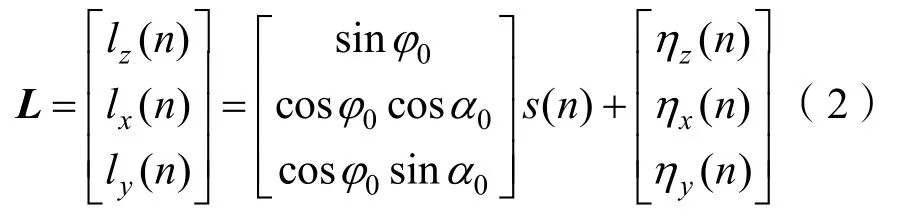

则输入信号的空间谱P(φ,α)为

式中:P(φ,α)是与俯仰角φ、方位角α的函数,反映了三轴投影模型对目标位置的分布估计。

式中:N是数据长度;C是L的自协方差矩阵。

2 基于鲁棒卡尔曼估计的融合跟踪
2.1 鲁棒卡尔曼估计
鲁棒估计是指在出现异常量测的情况下,利用适当的方法对目标状态进行估计,减小异常量测值对状态估计带来的误差。当出现观测野值时,传统的卡尔曼滤波算法在对状态进行估计时会产生较大的误差。为了对目标状态进行稳健的估计,人们将鲁棒统计学应用于滤波算法中,提出了基于Huber方法的线性卡尔曼滤波算法,实质是一种广义极大似然估计的卡尔曼滤波算法[10-11]。文献[12]在线性鲁棒卡尔曼滤波的基础上,揭示了Huber方法在滤波算法中对卡尔曼增益和状态估计的影响,并基于此推导基于UKF的非线性鲁棒滤波算法,以避免线性化带来的额外误差。
考虑如下的运动目标

其量测方程为
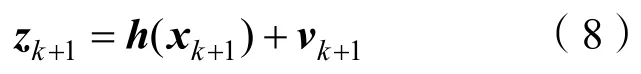
构造非线性回归方程

定义如下变量

则
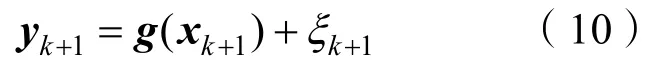
Huber代价函数定义为



那么其相应的φ函数为

要使得代价函数最小,则





Huber方法改进后的 UKF算法等效量测噪声为

由上述过程可知,NHUKF算法没有对非线性方程的线性化过程,避免了 HUKF算法带来的线性化误差,同时NHUKF算法利用Huber方法对量测异常值进行处理,能抑制异常值对目标状态估计带来的影响。
2.2 仿真实验及分析

表1 仿真参数Table 1 Simulation parameters

表2 滤波器初始状态Table 2 Initial parameters of filter

图2 EKF与UKF跟踪性能对比Fig.2 Comparisons of tracking performance between EKF and UKF
从图2仿真结果可以得出,双磁场传感器的跟踪性能要远优于单磁传感器的跟踪性能,在同等信噪比和滤波器初值的情况下,双磁场传感器的跟踪精度普遍比单磁场传感器的跟踪精度高10倍,而且当初始跟踪偏差进一步增加时,单磁传感器跟踪发散,而双传感器的跟踪仍会收敛。另外,比较可知UKF的跟踪精度要略优于EKF的跟踪精度。而实际的跟踪会出现异常量测值,因此设定量测噪声服从混合高斯分布


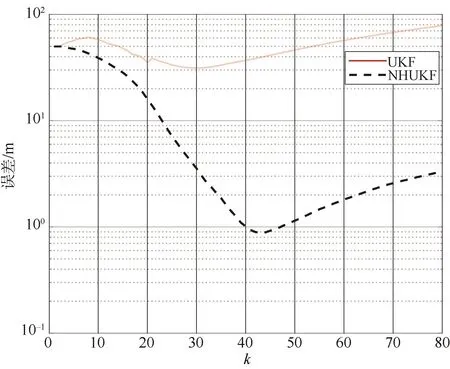
图3 UKF与NHUKF跟踪性能对比Fig.3 Comparisons of tracking performance Between UKF and NHUKF
前述的磁跟踪都是在信噪比较高情况下的跟踪,但当目标距测量点较远时或者目标的磁矩过小时,目标的跟踪精度则会严重降低,为此在原点位置处引入一个三轴地震动传感器作为观测站提供方位信息(采用1.2节中的方位估计算法估计目标的方位角),地震动角度估计偏差为2°。
如图4所示是NHUKF滤波器的跟踪结果,在有无异常观测值的情况下,地震动信息的引入都可以明显改善弱信噪比条件下的磁跟踪精度。因为双场磁传感器对于单偶极子磁性目标跟踪而言,其信息是完备的,所以地震动信息只能在磁信噪比较低的情况下改善跟踪的性能。

图4 地震动信号对跟踪性能的影响Fig.4 Effect of seismic signal on tracking performance
3 地磁融合跟踪试验结果
为进一步验证NHUKF算法的跟踪性能,在某试验场开展了陆地测量试验,验道路长度约400 m,略带弧度。实验道路为硬质土路,路面含有少量沙石,3个传感器节点布置在实验道路一侧,呈一条直线,相距5 m,距离道路正横距离约10~20 m。如图5所示是搭建的分布式测量系统,包括3个节点,每个节点由1个加速度计和1个磁传感器组成。所有节点的磁传感器测量的数据通过数据采集卡送至计算机,而加速度计测量的数据也通过采集控制电路信号监视与采集端。通过NI DAQ软件集中对磁信号和地震动信号数据进行处理和存储。

图5 分布式测量系统Fig.5 Distributed measurement systems
分布式传感器实验系统包括3个节点,传感器节点1的坐标为[-5,0],传感器节点2的坐标为[0,0],传感器节点3的坐标为[5,0],每个节点由一个Model 203加速度计和一个Mag03磁传感器组成,测量目标为小型卡车。
如图6所示,分别是正向运动舰船磁信号C1的跟踪结果和反向运动舰船磁信号C2的跟踪结果。可以看出目标与传感器距离最近时,跟踪误差都可以稳定在5 m以内。主要的误差来源在于2个传感器的三轴指向不完全平行以及参考轨迹不完全准确。要进一步验证算法的性能,可进行更精细化的合作目标固定轨迹实验。

图6 跟踪结果Fig.6 Tracking results
由于实测地震动信号的方位估计角偏差过大,引入后会降低算法性能。从本质上看,地震动不能认为是直达波,其传播机制具有多径效应,另外受地形地质等因素影响很大,所以多方位估计性能较差也在所难免,地震动传播模型和场源模型还有待进一步研究。目前的测量数据和处理结果表明,地震动信号适合作为一种远程探测信号。
4 结束语
铁磁性舰船目标运动过程中会产生磁、地震动等多物理场信号,舰船目标的单一物理场所获取的信息量比较有限,本文结合多节点测量的目标地震动和磁场信息,提出了一种鲁棒的地震动-磁场信息融合的跟踪算法,仿真实验表明算法能够有效降低异常观测值带来的影响,另外双节点三分量磁场的信息比较完备,地震动信息只能在磁信噪比较低的情况下改善跟踪的性能。

