水下电偶极子跟踪定位系统可观测性分析

喻 鹏，程锦房，张伽伟，肖大为

（海军工程大学 兵器工程学院，湖北 武汉 430033）

0 引言

源于舰船腐蚀、防腐电流的水下电场信号是舰船目标的重要暴露源[1-2]，可基于目标自身的电场矢量信息对目标进行定位，具体应用算法主要有解析反演和滤波估值[3-4]。

解析反演法即利用目标电场的信息，采用矢量计算的方式直接求出目标的位置信息，具有计算小，实时性好的特点，但受噪声和模型误差影响较大。目前更为有效的方式是滤波估值法，其主要是基于贝叶斯滤波框架，将目标定位问题建模为基于贝叶斯理论的最优估计问题。也就是基于观测方程和状态方程对目标实际状态不断进行最优估计，从而获取目标位置、速度、航向等信息，主要算法有卡尔曼滤波和粒子滤波以及它们的衍生算法。如文献[4]和[5]将扩展卡尔曼滤波算法（EKF，Extended Kalman Filter）应用于船舶的静电场跟踪，之后文献[6]又研究了电场传感器阵列的排列方式和传感器数量对电场目标跟踪误差的影响。文献[7]是基于GLRT（Generalised Maximum Likelihood Ratio Test）和蒙特卡洛准则，利用水下电场信息对目标位置、航向角等状态的估计。

可以看出，上述文献重点是从算法应用方面评估电场跟踪的效果，但是这种跟踪效果受环境噪声强度、观测站数量、目标模型误差等因素影响较大。为了从理论上分析不同参数对跟踪效果的影响，本文基于可观测分析理论，对单观测站条件下的电偶极子跟踪系统的可观测性和不同参数的可观测度进行分析，之后也对比了双观测站与单观测站在可观测度上的差异。（注意，对于潜艇等水下目标的电场特征，国内外普遍采用电偶极子模型的对其电场分布进行建模[8-9]，所以文中在进行可观测性分析时，将目标等效为电偶极子模型。）

1 可观测分析理论

由于观测方程是非线性的，所以根据 Lee和Dum等人提出的可观测定理进行分析[10]。

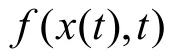
如果对于凸集S∈Rn上所有x0，如果都能够使得式（2）是正定的，则系统在S上是完全可观测的。

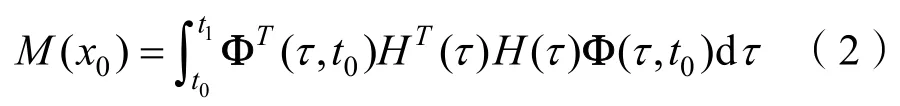
其中

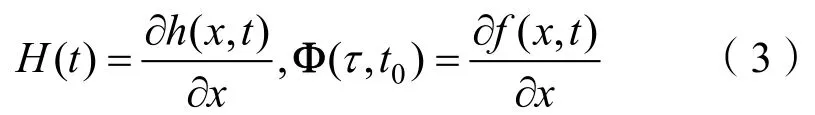
对于离散系统，上述结论可等价为[10-11]：对于初始集合S中的矢量Xk，记 Gramer矩阵如式（4）所示。其中：k为离散时间变量；Φ为状态转移矩阵。

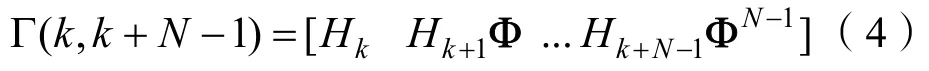
其中Jacobi阵Hk具有如下形式

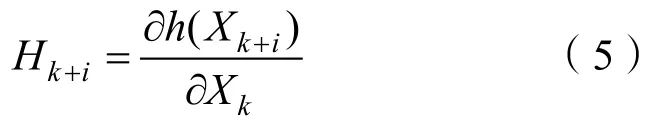
另外，为了度量系统受噪声影响的程度，在系统可观测的基础上，应该估计系统的可观测度大小，可观测度越大，该状态量更容易估计。基于牛顿迭代解法，可知状态估计的协方差为

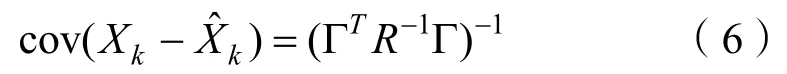
2 目标电场跟踪模型建立

由于空气和海床的电导率远低于海水电导率，在浅海环境或者靠近海面、海床附近位置，应该考虑界面反射对水下电场传播带来的影响[13]。但是由于这里只是对系统的可观测性进行分析，如果考虑界面反射带来的影响会导致运算量大幅增加，并且由界面反射在测量点所产生的电场只占总场中的较小部分。所以本节在进行可观测分析时，将电场传播模型近似为单层介质模型，即不考虑界面反射带来的影响，该近似对系统的可观测性分析影响较小。

对于水下目标，可将其等效为电偶极子模型，定义水平方向和垂直方向的电偶极子源强度分别为Ph和Pv。考虑到目标常规运动状态，这里假设目标在水中固定深度进行匀速直线运动，所以系统状态量为

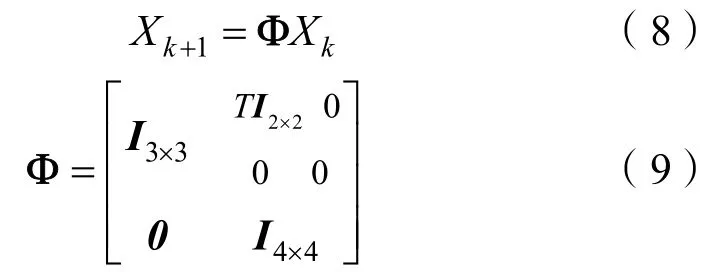
根据电偶极子电场分布模型[14]，可知测量点（即观测站）位置处的电场应该为水平电偶极子源强度和垂直电偶极子源强度在该测量点产生的电场矢量和，设定测量点坐标为(0,0,h)，则该位置处的电场如式（10）-（12）所示。

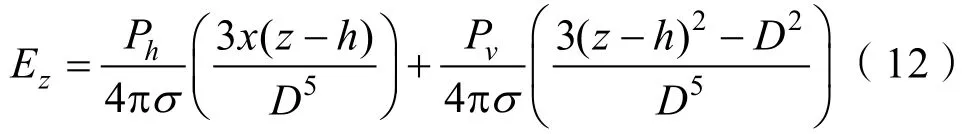
式中：σ为海水电导率；θ为目标运动方位角；D为测量点与电偶极子目标之间的直线距离。

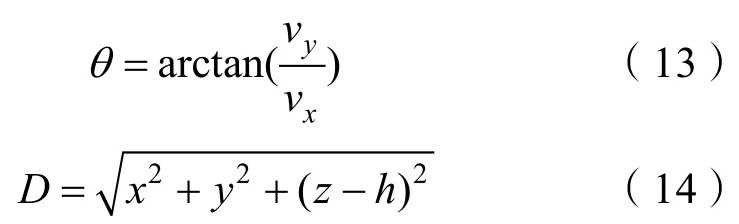
另外在计算时，将电偶极子视为稳恒点电源，即电偶极子源强度P=I·L，I为2个点电极之间的等效稳恒电流，L为2个点电极之间的间距，对于水平和垂直电偶极子源强度Ph和Pv，他们的大小可根据实际舰船的电场源强度进行设定。

3 基于单观测站的水下电偶极子跟踪可观测性分析

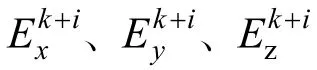
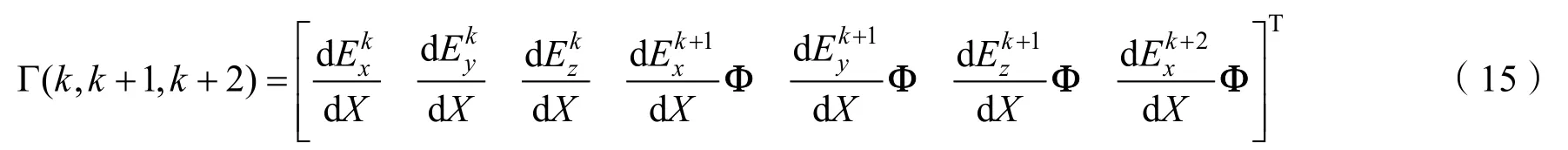
尽管观测方程已经化简，但是在求解Γ的秩时仍然运算量很大，这里借助数学工具Mathematic软件进行求解，运行结果显示rank（Γ）=7，初步判定系统具有可观测性。为了更加直观地判定系统是否可观测和其可观测度，这里采用计算行列式|det(Γ)|的方法，当|det(Γ)|≠0即可判定系统是完全可观测的，且|det(Γ)|越大，可观测度越高。

由于未知参数较多，这里采用假设已知部分参数，研究其余参数变化时|det(Γ)|的变化规律的方法，来确定目标（即电偶极子源）不同水平位置、垂直深度、水平和垂直电偶极子源强度对系统可观测度的影响，分析结果如下所述。

3.1 目标水平位置对可观测度的影响

由图 1可以看出不同水平位置x,y对应的|det(Γ)|值是不一致的，在靠近（0，0）位置附近，|det(Γ)|较大，也就是说目标越靠近观测站，系统的可观测度越高，这与实际实验结果是一样的。另外，也可以看出系统的可观测度并不是随着距离减小而线性增加，其变化率是趋近于指数增加，即目标越靠近观测站，其系统可观测度增加越迅速。

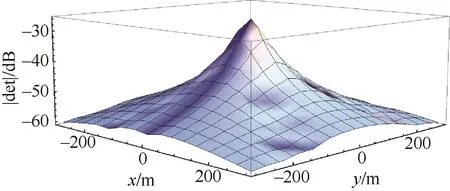
图1 不同水平位置（x,y）对应的|det(Γ)|Fig.1 Corresponding|det(Γ)|of different horizontal locations（x,y）

3.2 目标垂直深度对可观测度的影响

设定除x,z以外参数的值，Ph=1 00A·m，Pv=2 0A·m，h=100m，y=50m，vx=2 m/s，vy=2 m/s，T=1s。得到如图2所示的|det(Γ)|与x,z的关系图，注意这里也进行了不同y值情况下的仿真计算，得到的结果与图 2所得的趋势是一致的，所以图 2具有一定的普适性。

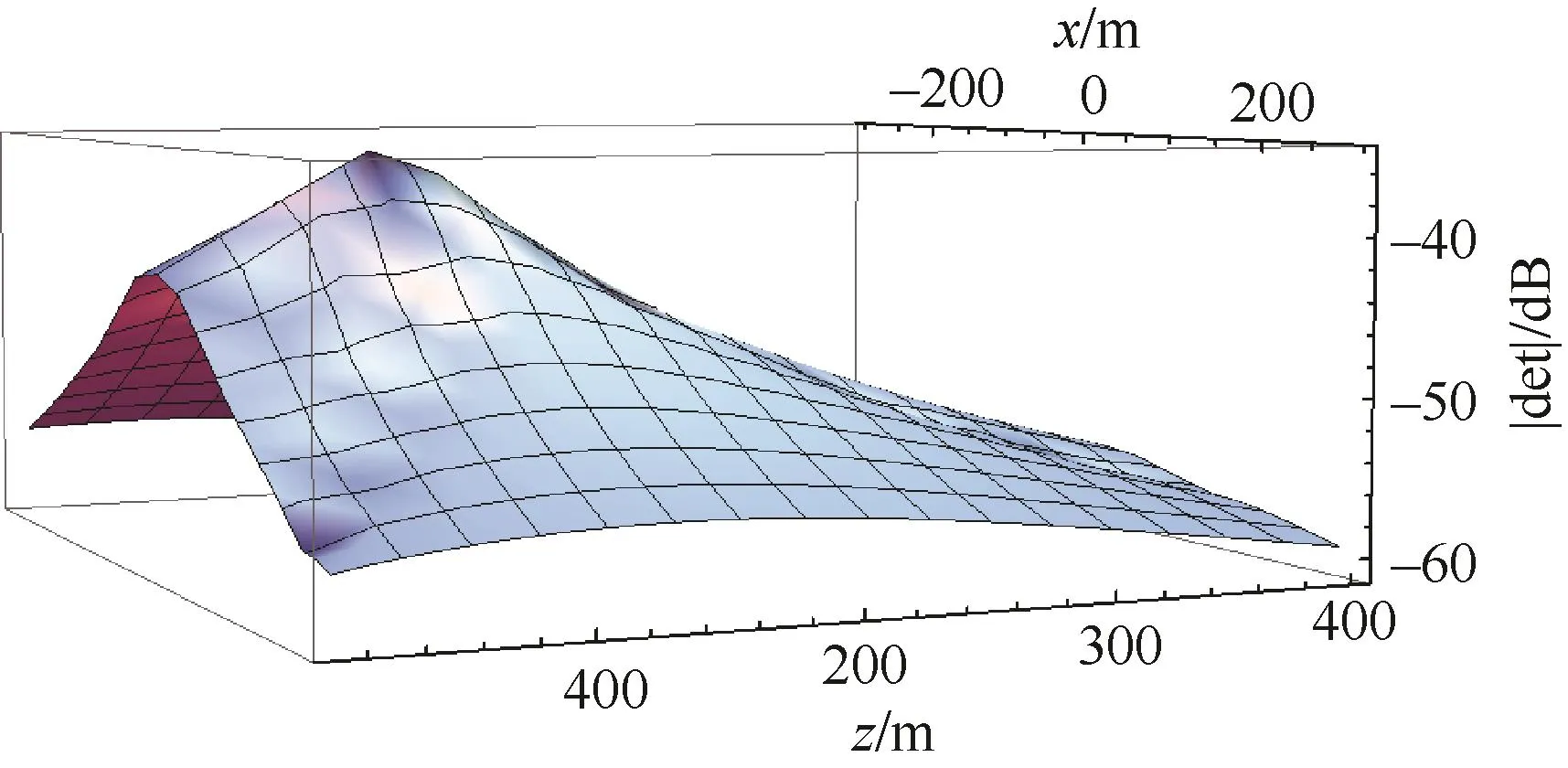
图2 Ph＞Pv情况下不同x,z值对应的|det(Γ)|Fig.2 Corresponding|det(Γ)|of different locations（x,z）when Ph＞Pv

由图 2可以看出在x=0，z=100 m位置处，|det(Γ)|最大，也即目标越靠近观测站系统可观测度越高。单独分析x轴和z轴变化对|det(Γ)|的影响，定义z=100 m时，x由0增大至300 m产生的|det(Γ)|衰减值为Δ|det(Γ)|x，x=0时，z由100 m增大至400 m产生的|det(Γ)|衰减值为Δ|det(Γ)|z，即对比在水平和垂直方向上同样距离对|det(Γ)|的影响，由图2可以看出Δ|det(Γ)|x小于Δ|det(Γ)|z，经过分析发现这是由Ph大于Pv导致的，因为电偶极子源强度水平分量大于垂直分量，导致|det(Γ)|在水平方向上衰减小于垂直方向上。为进一步验证，将Ph和Pv均设定为100 A·m时，结果显示|det(Γ)|在水平方向和垂直方向上的衰减速度基本是一致的，说明水平位置和垂直深度的可观测度分别与水平和垂直电偶极子源强度相关。

3.3 目标电偶极子源强度对可观测度的影响

研究电偶极子源强度总强度、水平和垂直电偶极子源强度相对大小对系统可观测度的影响。仍然在3.1节的基础上，通过改变水平和垂直电偶极子源强度的大小，分析|det(Γ)|的变化。图3为将水平和垂直电偶极子源强度均增大为原来的10倍时对应的det(Γ)|值减去原始det(Γ)|值得到的Δ|det(Γ)|，由于Δ|det(Γ)|变化范围较大，所以图中纵坐标为Δ|det(Γ)|的对数值，当Δ|det(Γ)|＜0时图中应为空白。

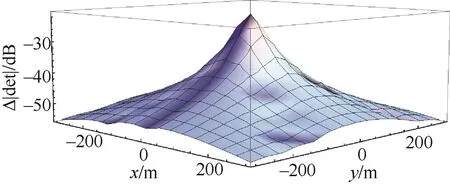
图3 电偶极子源强度增大时对应的 Δ|det(Γ)|Fig.3 Corresponding Δ|det(Γ)|when electric dipole source intensity is increasing

可以看出随着电偶极子源强度增大，系统的可观测性是增大的。另外，通过|det(Γ)|的计算公式也可以看出，|det(Γ)|与电偶极子源强度成明显的正比例关系，所以增大电偶极子源强度强度，|det(Γ)|必然增大。

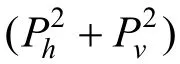
图4 电偶极子源强度对|det(Γ)|的影响Fig.4 Effects of electric dipole’s source intensity on|det(Γ)|

由图4（a）-（c）可以看出，当电偶极子源强度逐渐由水平分量转换为垂直分量时，会导致观测站附近的可观测度降低（图中空白区域代表Δ|det(Γ)|＜ 0），而在其他较远位置，可观测度增加。说明电偶极子源强度水平分量和垂直分量增大对不同水平位置的可观测度影响是不一致的，其中电偶极子源强度水平分量增大能够在较大范围内增大系统的可观测度，而电偶极子源强度垂直分量增大只会在目标贴近观测站时增大系统的可观测度。另外，为分析目标垂直深度z对Δ|det(Γ)|的影响，也在不同深度z进行和图4（a）-（c）一样的仿真计算，也得到近似的结果，只是目标与观测站的垂直距离越小，图4（a）-（c）中心的空白区域越大。

4 基于双观测站的水下电偶极子跟踪可观测性分析

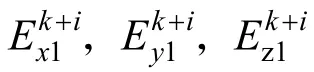
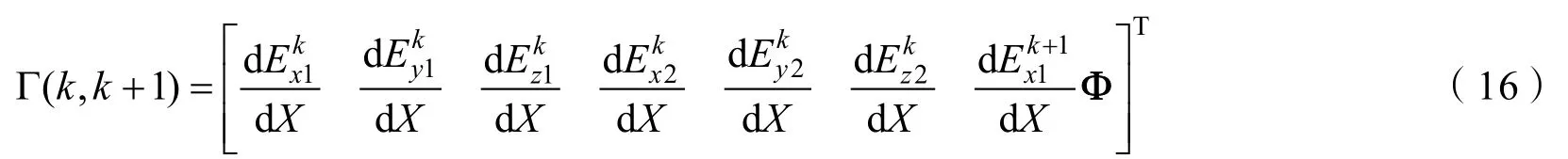
为便于计算，这里设定观测站2的坐标为(d,0,h)，2个观测站之间的距离为d（观测站1的位置仍为(0,0,h)）。所以这里的观测方程与单观测站的观测方程是一样的，只需在计算观测站2的测得的电场时，要将观测站的坐标改为(d,0,h)，这里省略计算过程。

由于第3节已经分析了目标位置和偶极子源强度对可观测度的影响，所以这里只选取典型的目标运动特征参数，分析单、双观测站的可观测度差异以及双观测站之间的间距d对可观测度的影响。

4.1 双观测站相比单观测站的可观测度

设定 Ph=1 00A·m，Pv=20A·m，h=100m，z=1 20m，vx=2 m/s，vy=2 m/s，T=1s。之后设定双观测站之间的间距d，这里首先设定d为一较小值d=2 m。分别计算基于单观测站和双观测站系统的可观测度，同时用后者减去前者得到可观测度的差值Δ|det(Γ)|，图5（a）所示。

可以看出，图5（a）中部分区域是空白的即对应Δ|det(Γ)|＜0，部分区域非空白即对应Δ|det(Γ)|＞0，说明在双观测站间距较近的情况下，双观测站的可观测不一定大于单观测站。主要是由于双观测站之间距离太近，2个观测站所获取的目标信息基本一致，可观测度并不能明显增加。

所以继续增大双观测站之间的距离d，使d=15 m，得到如图5（b）所示的Δ|det(Γ)|差值，可以看出增大双观测站之间的间距后，其系统可观测度在整个水平范围内均大于单观测站对应的系统可观测度。

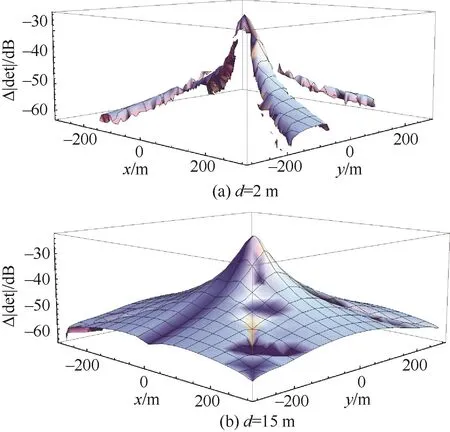
图5 双观测站减去单观测站对应的|det(Γ)|Fig.5 CorrespondingΔ|det(Γ)|when double observation station minus single observation station

4.2 双观测站之间的间距对可观测度的影响

由图5可以看出增大双观测站之间的间距，能够一定程度增大系统的可观测度，为进一步研究双观测站之间的间距d对可观测度的影响，进行如下计算。设定双观测站的间距d分别等于10 m、20 m、50 m、100 m，以d=10 m对应的|det(Γ)|作为基准，依次用其他间距对应的|det(Γ)|减去该基准，研究Δ|det(Γ)|与d之间的关系如图。

由图6（a）-（c）可以看出，随着d逐渐增大，在观测站附近出现的空白区域也逐渐增大，说明随着d逐渐增大，会导致观测站附近的系统可观测度降低，而在其他较远区域的系统可观测度增大。这一点也可以这样理解，由于2个观测站之间距离较大，当目标逐渐靠近观测站时，必然会导致此时两个观测站所获取的信号强度低于观测站间距较小对应的接收信号强度，那么其系统可观测度必然会降低。所以在实际选择观测站之间的间距时，需要根据目标信号的辐射区域强度进行选择。注意图6中的空白区域不在图像正中央是因为双观测站并不是关于原点对称，而是观测站1始终位于原点位置。

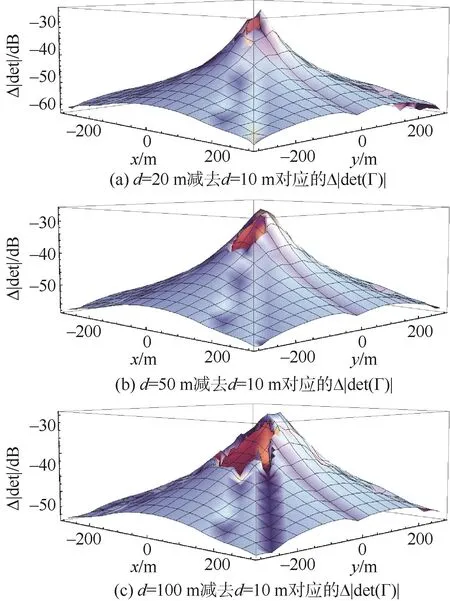
图6 不同观测站间距d对应的 Δ|det(Γ)|Fig.6 Δ|det(Γ)|corresponding to different distances between two observation stations

5 结束语

基于可观测分析理论，分析了单观测站条件下的水下电偶极子跟踪定位系统的可观测性，以及电偶极子水平位置、垂直深度和电偶极子源强度的对系统可观测度的影响。之后也对比了双观测站与单观测站可观测度的差异，以及双观测站间距对可观测度的影响。

综合上述可观测分析，可得到如下结论：1）基于单观测站的电偶极子源跟踪定位系统是可观测的，电偶极子越靠近观测站，系统的可观测度越高；2）目标水平位置x，y与垂直深度z的可观测度与水平、垂直电偶极子源强度大小分布正相关，当垂直电偶极子源强度小于水平电偶极子源强度时，目标的深度信息可观测度要低于水平位置信息，所以对于实际水下目标（垂直电偶极子源强度只占目标等效电偶极子源强度较小一部分），目标垂直深度估计比水平位置估计难度更大；3）双观测站系统的可观测度大于单观测站系统的可观测度，但是必须保证双观测站之间的间距较为合适，当双观测站之间的间距过大时，会导致靠近观测站附近的系统可观测度降低。