基于测试标准的大规模储能电站建模与仿真

刘星宇， 徐少华， 李相俊， 韩晓娟

(1.中国电力科学研究院有限公司，北京100192；2.华北电力大学控制与计算机工程学院，北京102206)

近年来，电化学储能技术的商业化已较为成熟，国内先后建成了数十座大规模电化学储能电站，并建立了包含电化学储能系统检测指标、检测方法、检测流程和检测平台的储能系统检测评价体系[1-2]。随着电网规模的扩大，单台储能变流器(power converter system，PCS)无法满足输电能力的要求，通常采用多PCS 并联提高电站输电能力。然而由于并网阻抗的存在，多机并联的拓扑关系结构会引发PCS 间相互耦合，影响系统稳定性，单靠测试设备对储能系统进行测试与评价已经不能满足要求。因此，需要在原有研究的基础上，基于储能系统实际测试数据建立可真实反映储能系统输出特性的仿真模型，并根据不同时间尺度条件下的仿真结果分析并网稳定判据，为实际储能系统的运行维护提供参考依据[3-5]。

PCS 多机并联后通过变压器接入母线是现阶段储能电站的主流拓扑结构。以青海格尔木时代新能源光伏储能电站为例，该项目为50 MWp 光伏电站，配置了15 MW/18 MWh 磷酸铁锂电池储能系统，用来提高光伏电站的可调度性，促进电网和光伏发电的协调发展，并减少弃光电量，项目于2016年开始并网发电，属于大规模储能与发电站联合运行的典型案例。该储能电站的拓扑结构如图1 所示，储能系统以3 MW 为一个单元，每个单元经过6 台500 kW 储能变流器接入一台3.15 MVA 升压变的低压侧母线，升压至35 kV 后再通过110 kV 升压站接入变电站。

图1 青海格尔木时代新能源光储电站单元拓扑图

目前已有相关文献，对PCS 多机并联乃至大规模储能电站的建模进行了一定研究，文献[6]基于下垂控制设计了2 台PCS 并联接入微电网的仿真系统，并分析了模型参数对PCS及并联系统的影响；文献[7]使用诺顿等效电路搭建了多台PCS 并联仿真运行模型并对其稳定性进行了分析，但单台与并联的规格均与现役主流储能电站不符；文献[8]参照光储系统结构搭建了光储联合电站模型从而研究储能设备在电站控制中的应用，但未考虑到具体电站拓扑结构；文献[9]以调度特性作为基础搭建了电池储能系统优化调度模型，但无法表征系统内部运行特性。同时，上述文献在对系统稳定性进行判定时均未考虑不同PCS 间的参数差异与具体拓扑结构的影响。

综上所述，本文以实物电站作为研究对象，首先按电站规格对单体PCS 参数进行设计，并通过设定参数取值范围体现各单体间的差异；之后通过一种dq 坐标系下的全解耦控制策略，消除了多PCS 间耦合对系统稳定性的影响；然后根据电站拓扑结构连接各PCS，完成大规模储能电站的等值建模；最后基于现行储能电站检测标准对电站模型进行仿真，并通过与实测数据的对比验证所建模型的性能，为实际储能系统检测提供参考依据。

1 储能电站建模

1.1 PCS 参数设计

储能PCS 的主要组成部分为逆变器与滤波器，其中LCL型滤波器因其对高次谐波的优良衰减效果与低开关频率下的性能优势，在实际应用中逐渐代替了传统的L 型滤波器[10-11]。图2 为三相并网逆变器拓扑结构图，图中VT1-VT6代表左侧三相逆变电路的各个IGBT 开关管，R1为变流器侧滤波电感L1的等效内阻，R2为网侧滤波电感L2的等效内阻，C 为LCL 滤波器的电容。

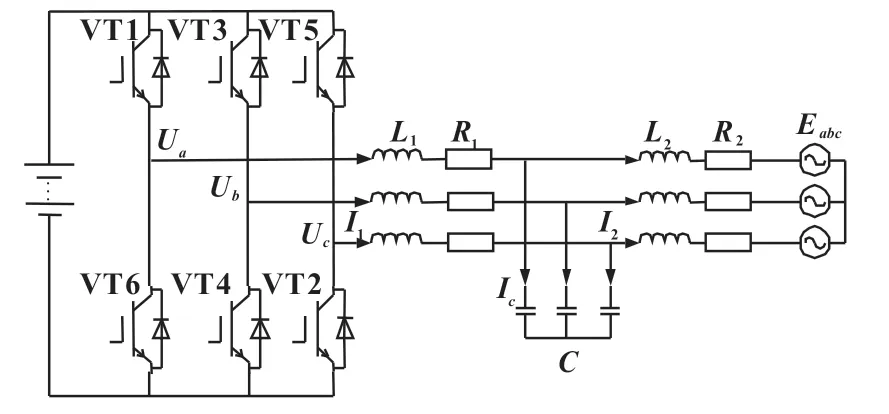
图2 PCS 并网运行拓扑

由文献[12-14]的分析可以总结出，滤波器参数的设计原则应满足在尽量节省电感磁芯材料的条件下，使得滤波效果最好，同时需要保证谐振频率不能过小，以免对电流控制器的设计提出过高要求。LCL 滤波器的参数选取应遵守以下条件：

(1)LCL 滤波器因自身电感会产生阻抗，阻抗导致的压降应小于额定电网电压的10%；

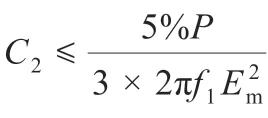
控制策略部分采取传统的PI 控制器，按照文献[8]的方法首先使用dq 变换对abc 坐标系下的三相电流进行转换，从而实现dq 轴分量的解耦，然后采用电容电流作为反馈量进行PI控制，最后通过SPWM 调制输出控制信号。同时，由于数台PCS 处于并联状态，各PCS 以公共耦合点(point of common coupling，PCC)电压Upcc并入电网。Upcc与电网电压之间的耦合关系为：

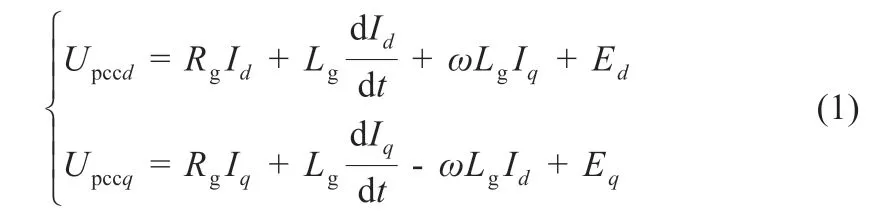
式中：Upccd和Upccq分别为Upcc在d 轴和q 轴的电压分量；Rg和Lg为滤波器并网产生总阻抗的等效电阻及电感；Id和Iq分别为并网电流的dq 轴分量；Ed和Eq分别为并网电压的dq 轴分量。因储能系统一般只产生或接收有功功率，即Iq可以忽略，Upccd受Id的影响较大，在dq 轴控制中使其为0，即可消除耦合。同时PI 控制的作用系统的无差性可以得到保证。在对dq 坐标系下的储能系统进行全解耦后，采用图3 所示的电容电流反馈控制来实现对并网电流的控制。

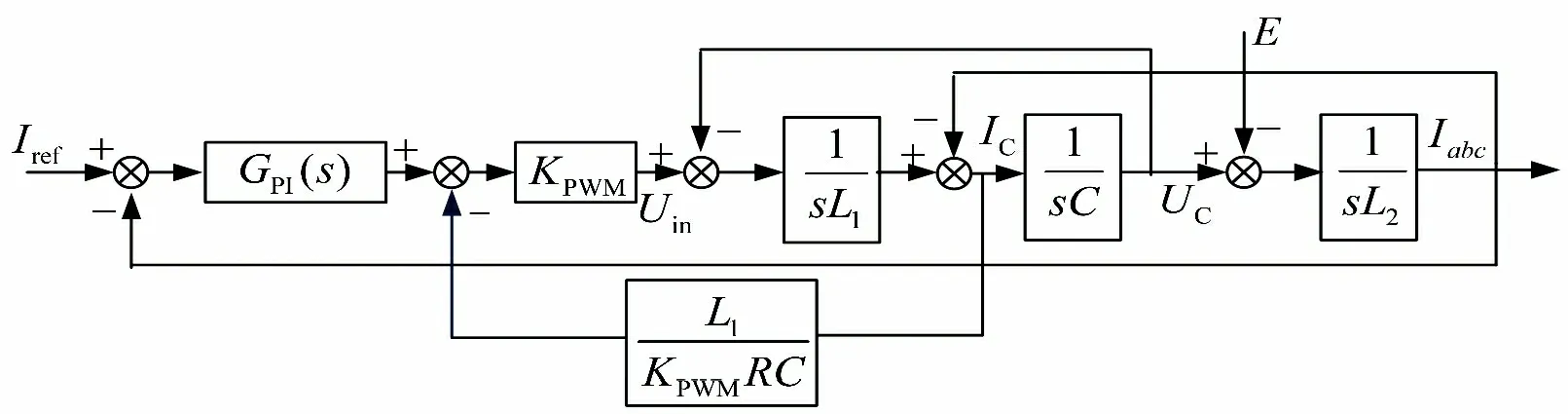
图3 PCS电容电流反馈控制框图

通过叠加定理，可求得PCS 的并网输出电流表达式为：

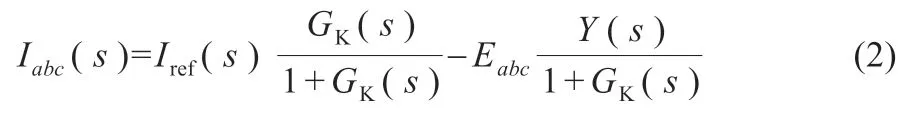
其中：

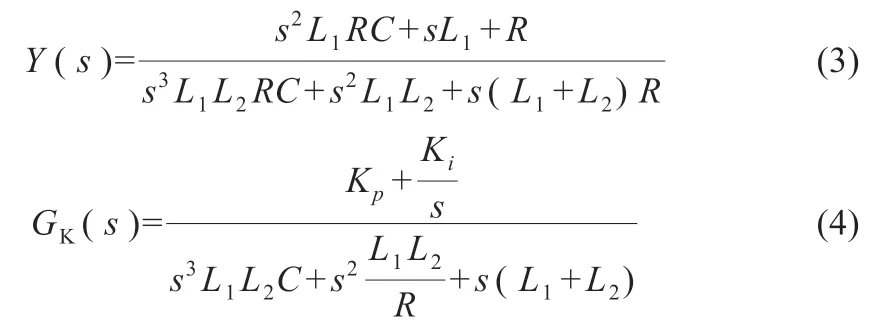
式中：Kp和Ki为PI 控制器的比例系数与积分系数；R 为反馈控制需要设定的虚拟电阻。由式(2)可知，并网电流Iabc中PI 控制参数对系统稳定的影响体现于式(2)中1+GK(s)的系统稳定性。同时由式(4)可知，微分系数对系统稳定性的影响较小，但通过绘制不同比例增益下的Bode 图可以在保证系统稳定的前提下求出合适的比例系数。

首先设定Ki=103，对比例系数进行整定：分别在Kp=0、20、40、60、80 时，画出系统的Bode 图，如图4 所示。

由图可见，Kp=40 时的系统频率响应曲线谐振尖峰抑制效果最好，控制系统闭环稳定，而且相角裕度满足了系统良好的动态追踪性能。然后在Kp取值为40 时使用传统PI 参数整定方法进行整定，最后求得的控制效果最优的微分系数i为Ki=2.85×103。

图4 Kp取不同值时的Bode图

考虑到实际电站中各PCS 的电子元件的参数一致性较差，在仿真模型中滤波器的滤波电感与电容均通过设定取值范围的方式随机取值。综上所述，PCS 各项参数取值见表1。

1.2 变压器参数设计

参照图1 的电站拓扑图，多台PCS 并联接入母线需要经过10 kV/380 V 三相变压器。出于贴近实物的目的考虑，仿真铁芯设定为不饱和[17]，三相变压器的类型选择为三个单相变压器组合实现，双绕组联结方式变压器两侧均选择为中性点接地的Y 连结方式[18]。变压器的各项参数取值见表2。

1.3 Simulink 平台的储能电站模型

储能电站模型的搭建平台选用Simulink 平台，该平台自带的Simpowers 元件库可以支持对储能电站的关键部分三相电桥和变压器进行简单的仿真，同时也便于对后续的数据进行处理。以图1 的青海格尔木时代新能源光伏储能电站拓扑作为参考对象，将1.1 中设计的500 kW PCS 单体共30 台，每6台并联作为一个3 MW 单元并通过变压器接入汇流母线，即可搭建出如图5 所示的储能电站仿真模型。

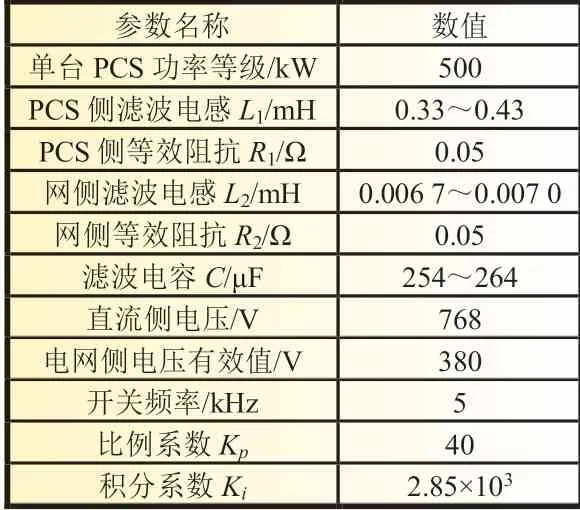
表1 PCS 仿真参数

表2 三相变压器相关参数 p.u.

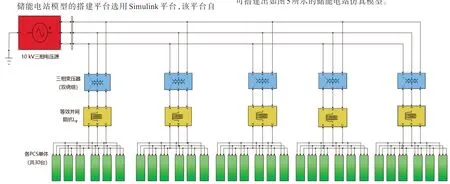
图5 Simulink 平台储能电站仿真模型

2 基于测试标准的大规模储能系统接入电网仿真分析

标准GB.T 36548-2018《电化学储能系统接入电网测试规范》的主要适用对象为额定功率100 kW 及以上，可在额定功率放电工况下工作15 min 以上的于35 kV 以下电压等级电网工作的并网型储能电站，对该种电站的设备与测试相关内容进行了规定。参照该标准对大规模储能系统仿真模型进行测试，并将仿真结果与南瑞电气设备与工程能效测评中心出具的青海格尔木时代新能源光储电站15 MW/18 MWh 储能系统的检测报告结果进行对比，从而对仿真系统的性能进行验证。其中，各项测试的仿真采样步长均为5×10-6s，实测值的数据粒度则因测试项目而有所分别。

2.1 充放电调节时间测试

具体测试方法为：在系统处于热备用状态时，向储能系统发送额定功率充放电指令，记录开始放电时刻；然后当放电功率偏差维持在储能系统额定功率的2%以内时，该时刻与开始放电的时间差值为放电调节时间；重复以上操作两次，取最大调节时间作为测试结果。

图6 和图7 为三次测试中采用为测试结果的充放电功率调节时间仿真与实测曲线，其中实测数据的采样步长为4×10-5s。仿真与实测的调节时间对比如表3，仿真系统充放电调节时间与实测值基本一致(误差在15 ms 以内)，证明了仿真系统的有效性。

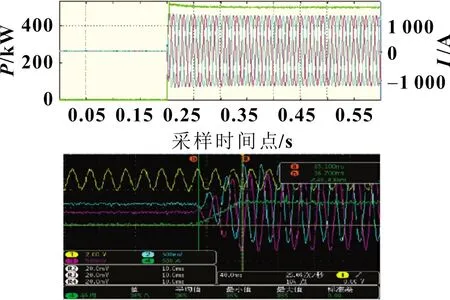
图6 放电功率调节时间测试曲线

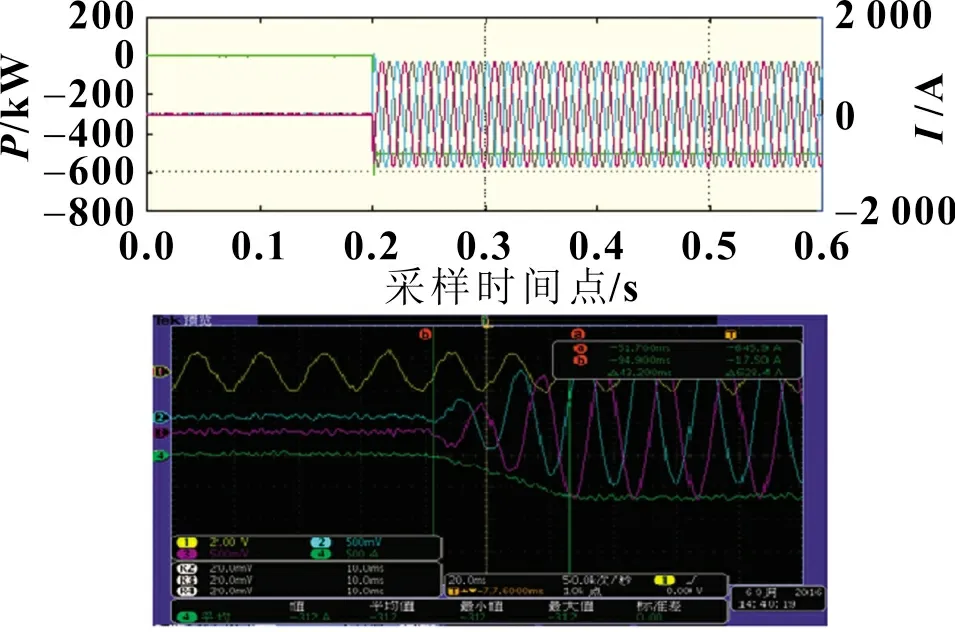
图7 充电功率调节时间测试曲线

表3 充放电调节时间对比 s

2.2 有功功率调节能力测试

有功功率调节能力的测试分两步:第一步按固定差额逐渐增加设定充放电有功功率并观察控制效果;第二步则是在额定功率附近不断改变功率值，来对储能系统正常运行中可能出现的功率微调工况进行模拟。

2.2.1 梯度功率变化充放电有功功率测试

具体测试方法为：按图8 所示，设置系统初始有功功率为0，然后调节放电或充电有功功率至±0.25P额定、±0.5P额定、±0.75P额定、±P额定，然后逐级降低充电或放电有功功率至±0.75P额定、±0.5P额定、±0.25P额定、0，记录对应的功率值和变化曲线。

图8 充放电有功功率测试设定曲线1

按测试步骤仿真后得到的梯度充放电功率曲线与实测功率曲线的对比见图9 所示，因仿真系统不存在实际系统的响应时间，故实验过程较实测快。其中实测数据取200 ms 作为数据计算时间窗，计算对应的有功功率平均值。在各额定功率数值下，功率曲线均可迅速调节至平稳，而且波形畸变率也较小。具体数值分析如表4，无论在充电还是放电阶段，控制效果稳定后平均绝对误差的仿真与实测值基本一致，误差在3 kW 以内。

图9 梯度功率充放电曲线与实测功率曲线对比

表4 梯度功率变化充放电有功功率测试数值分析 kW

2.2.2 额定功率附近功率变化有功功率测试

图10 所示为设置系统初始有功功率为0，调节有功功率至0.9P额定、-0.9P额定、0.8P额定、-P额定、P额定、-0.8P额定，各点保持一段时间，记录对应的功率值和变化曲线。

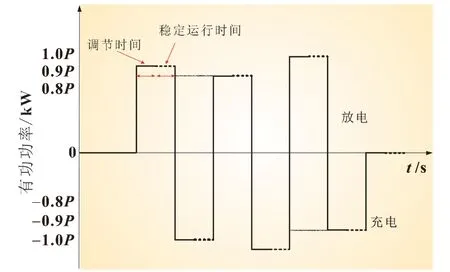
图10 充放电有功功率测试设定曲线2

按测试步骤仿真后得到的梯度充放电功率与实测功率曲线的对比如图11 所示。其中实测数据取200 ms 作为数据计算时间窗，计算功率平均值。该实验各设定功率比起梯度功率充放电实验更接近额定功率，具体数值分析如表5，仿真数据与实测数据的平均绝对误差与最大绝对误差基本一致。综合两个有功功率调节能力测试可以总结出，本文使用的储能系统模型可以适应储能系统出力需求，迅速调节功率，证明了系统在额定功率范围内的正常运行能力。

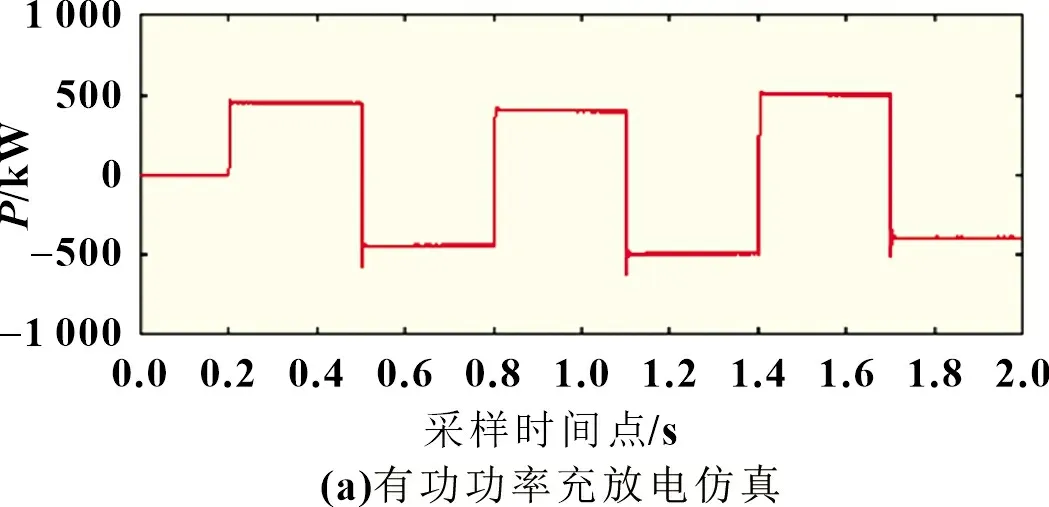
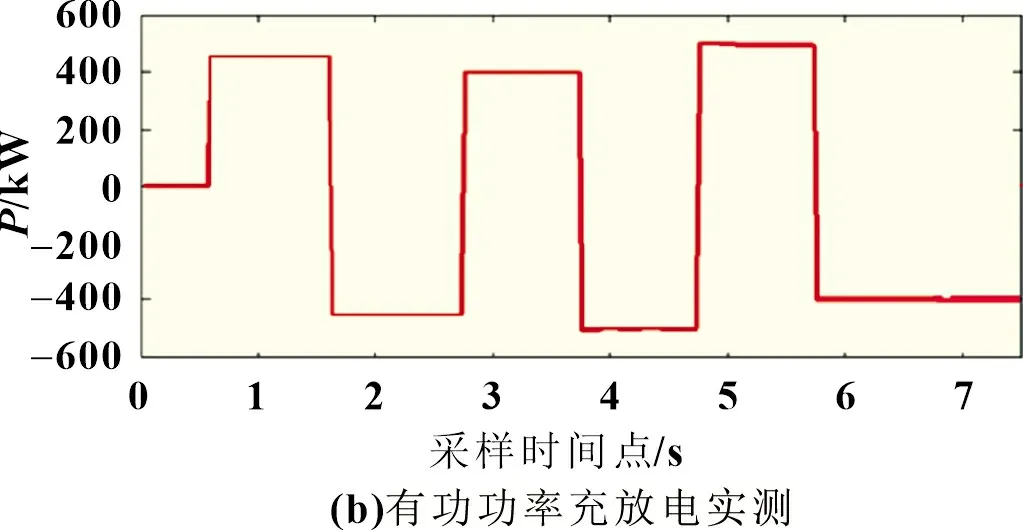
图11 充放电有功功率曲线

表5 充放电有功功率测试数值分析 kW

2.3 光储联合系统运行控制测试与对比

大型储能电站仿真中，如文献[19]中设计的光伏电站，往往各个储能单元、升压变压器、滤波器参数均相同，在稳态、短路等暂态工况下外部特性一致。故为减少仿真计算量，将整个仿真模型等效为一个整体，只包含单台储能逆变器，单台变压器与单条输电线路，从而将模型简化为整体等效模型。该种仿真模型着重研究电站的整体外部特性，可以更直观地表现整体电压与功率，同时仿真时间相对较短[19]。图12为光伏电站整体等效仿真模型的示意图。

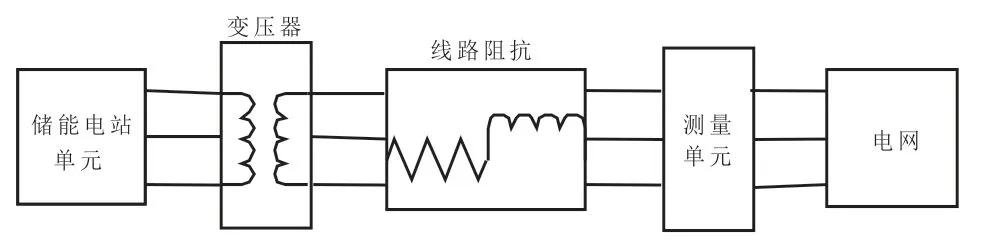
图12 储能电站整体等效仿真模型

作为建模对象的青海格尔木时代新能源光储电站15 MW/18 MWh 储能系统，其主要工作模式为接受光伏电站并网状态与出力调度，从而达到改善光伏电站输出特性，提升新能源消纳水平，与进行辅助调峰调频的功能。通过在并网状态下发布手动调度指令，可以对并网模式下的储能电站出力精度进行检测。

出力精度的测试基于手动模式下功率指令与接收到的功率值之差，出力精度误差=100%×(测量值-设定值)/设定值，按标准规定，合格的储能电站各项出力精度均不应低于90%。测试方法为：首先测试各PCS 出力精度，对1 到5 号储能单元的每一台PCS 有功功率设置为0，然后逐渐升高放电或充电有功功率到±100、±300、±500 kW，记录对应功率值，每次功率稳定后维持一段时间，再继续下发下一功率指令；然后以全站为规模测试出力精度，设置全站有功功率为0，逐渐升高充放电有功功率至全站最大有功功率的25%、50%、75%、100%，并记录对应功率值与出力精度。

对本文搭建的光储电站等值仿真模型与图11 所示的整体等效仿真模型分别进行出力精度测试，并将结果与在青海格尔木时代新能源光储电站15 MW/18 MWh 储能系统进行的同种出力精度测试进行对比，对比结果见表6。

表6 出力精度测试数值分析 %

由表6 的数值分析可以看出，两种仿真模型的全站出力精度范围与实测基本一致，其中本文所建模型因控制参数取值等原因与实测数据的出力精度差略大于整体等效模型，但在单PCS 出力精度方面，整体等效仿真模型因将整个模型等效为单台储能逆变器并网，仿真结果无法表现出某些PCS 单体因元件参数差异等原因导致的出力精度相对较低的情况。使用该种模型进行大规模储能电站建模，则可能导致全站出力精度符合标准，而PCS 单体出力精度不合格，从而对储能电站运行造成安全隐患。

3 结论

本文参照目标电站拓扑建立了适用于大规模储能电站的储能系统仿真模型，并基于相关测试标准对模型进行仿真分析并与实际储能电站的测试数据进行对比分析，验证了模型的有效性。具体结论如下所述：

(1)功率控制能力方面，实测数据与模型仿真结果均控制在40 ms 左右，而且仿真结果与实测值基本一致；额定范围内的功率曲线稳定后，最大绝对误差保持在额定功率的2%以内，而且仿真与实测值基本一致，误差在3 kW 以内；

(2)因各PCS 之间的耦合与参数一致性较差等原因，储能系统内部各单元的输电能力呈现出差异，并对系统稳定性产生影响。与传统的整体等效仿真模型相比，本文所建仿真模型可以表现出这种性能上的差异，预防并联系统谐振与个别单元不符合标准的情况；

(3)本文模型可以对储能电站暂态运行工况进行模拟，并在输出特性上与实际电站表现相近，为储能电站的运维提供了数据参考，同时为大规模储能电站运行稳定判据的研究提供了分析基础。