双极性锂离子电池热设计仿真研究

朱 峰， 何颖源， 陈永翀， 刘丹丹， 王玉伟

(1.中国科学院电工研究所，北京100190；2.北京好风光储能技术有限公司，北京100085)

近年来，锂离子电池作为一种响应速度快、调节精度高的电化学储能元件，在储能辅助调频领域得到了广泛应用。2019 年上半年全国调频补偿费用总额为27 亿元，并且其市场规模有望继续扩大[1]。电化学储能调频系统通常需要电池在数秒至数分钟内实现持续的大功率输入或输出，易导致电池系统局部出现热量集中，进而发展成为串并联电池间不可控的性能差异甚至安全问题[2-3]。

双极性锂离子电池采用了不同于传统锂离子电池的结构，通过在双极板两侧分别涂覆正负极活性材料，再以不同极性相对的顺序层叠，实现了电池单元的内部串联[4]。如此不但省去了大量电连接件，而且能够实现电极片间的电流垂直导通，缓解了电芯内部的电流不均匀问题，非常适合功率型储能应用场景。然而，为保证各串联电池单元的一致性，双极性锂离子电池在热设计过程中对控温及均温要求较高。Chen 等[5]通过建立双极性电池二维热模型，发现电池中心温度较为均匀，但是表面温度梯度较大。Pals 与Newman[6]分析了双极性锂电池放电过程中的热分布特征，发现电池中心与边缘的温差将随着放电过程的进行逐步增大。Tong 等[7]建立了双极性锂离子电池电化学-热二维模型，研究了液冷条件下的电池温度分布，结果显示电池温度不均匀性将受到电池尺寸、倍率及冷却方式等参数的影响。

在以往的研究中，由于双极性电池内部为层层串联结构，研究人员通常采用较为简化的二维模型进行温度分布研究，忽略了端部集流体在汇流过程对温度分布的影响。本团队在前期研究中发现虽然双极性锂离子电池内部电流分布高度均匀，但是当电流流经端面集流体时将受到汇流作用的影响，导致近极耳处的电流密度激增[8]。因此，本文通过建立三维热电耦合模型，分别研究了端部集流体厚度、极耳布置特征、电池尺寸与表面散热方式等参数对电池空间温度特征的影响，为双极性锂离子电池的热设计提供了理论基础。

1 建模方法

1.1 双极性锂离子电池几何模型

图1 为双极性锂离子电池结构示意图，电芯部分由众多电池单元串联而成，其中每个电池单元由正负极活性层及隔膜组成，各个电池单元之间设有边缘密封层保证相互独立，并通过双极板实现层间串联形式。由于双极性锂离子电池为多层叠加结构，并且高度方向与长宽方向的尺寸差异较大，给建模造成了一定难度，因此需要进行如下假设：(1)各电池单元具有相同的电化学反应；(2)将除端面集流体之外的电芯部分视为均一发热体；(3)在本研究所涉及的温度范围内，材料物性参数为常数。

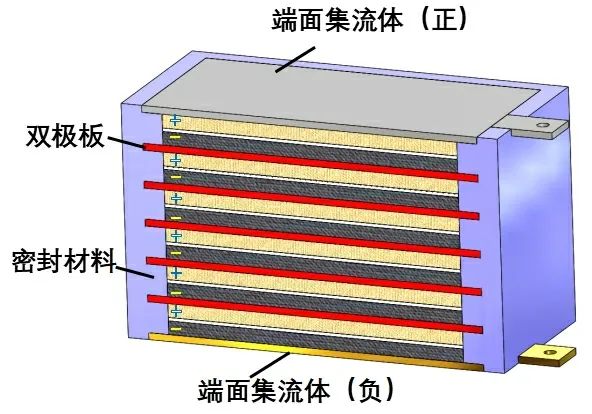
图1 双极性锂离子电池内部结构示意图

1.2 热电耦合模型

1.2.1 电化学模型

本研究以经典的P2D 电化学模型为基础构建双极性锂离子电池的电化学模型，具体流程与方程参照文献[9]。该模型主要由物质守恒方程、电荷守恒方程以及Butler-Volmer 电化学反应动力学方程组成。其中，固相守恒方程依据球坐标系下的菲克第二定律建立，电荷守恒方程为固体活性材料的欧姆定律形式，Butler-Volmer 方程用于体现电极颗粒表面的电化学反应速率，其表达式见式(1)～(3)：

固相守恒方程：

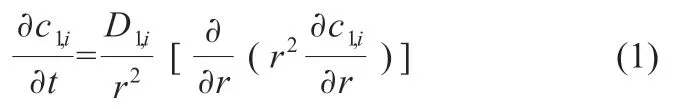
电荷守恒方程：

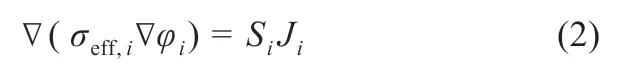
Butler-Volmer 方程：

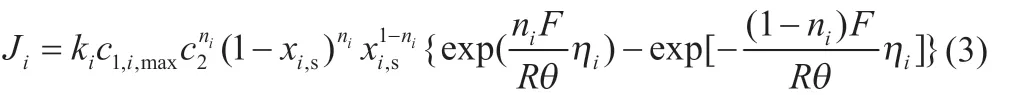
式中：c 为固相锂离子浓度；D 为扩散系数；r 为颗粒半径；下标i 代表正极或负极；σ 为电导率；φ 为电位；S 为电极颗粒活性比表面积；J 为电流密度；k 为反应速率常数；θ 为温度；η 为过电位；x 为固相表面浓度分数；n 为电荷传递系数，本研究依据文献[7]将其设置为0.5，下标1 和2 分别代表固相和液相，下标s 代表表面。

1.2.2 热模型

双极性锂离子电池在充放电过程中的产热主要由两部分组成，其一为电芯处的电化学反应热qe，该项生热可依据经典的Bernardi 生热理论进行计算；其二为端面集流体汇流过程中产生的焦耳热qc，可依据焦耳定律进行计算。因此，电池生热率表达式可按照式(4)进行计算。

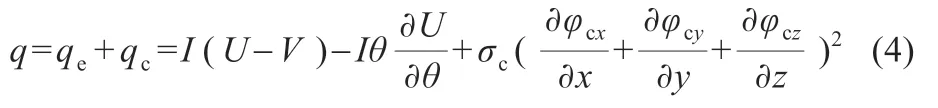
式中：I 为电流；U 为开路电压；V 为工作电压；σc为集流体电导率；φc代表集流体电位。U、V 与∂U/∂θ 均是荷电状态(SOC)的函数，可通过电化学模型计算得出。以生热率q 为源项，并且认为电池通过端面集流体进行对流散热，那么三维双极性锂离子电池能量守恒方程为：

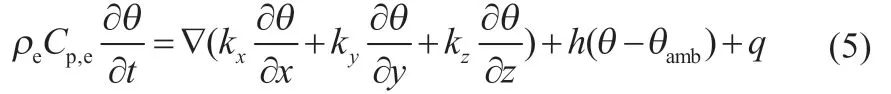
式中：ρe为模型的等效密度；Cp,e等效比热容；k 为等效导热系数；h 为对流换热系数。相关等效参数均按照复合材料混合定律进行计算。

1.3 电池物理性能参数及边界条件

本研究中采用磷酸铁锂/石墨活性材料体系，其物性参数如表1 所示。双极性锂离子电池规格为320 V/16.7 Ah，电芯尺寸为1 000 mm×500 mm×35 mm，极耳尺寸为10 mm×10 mm，以2 C 倍率持续放电1 400 s，初始温度为20 ℃，端面为自然对流散热条件，对流换热系数为5 W/(m2·℃)。

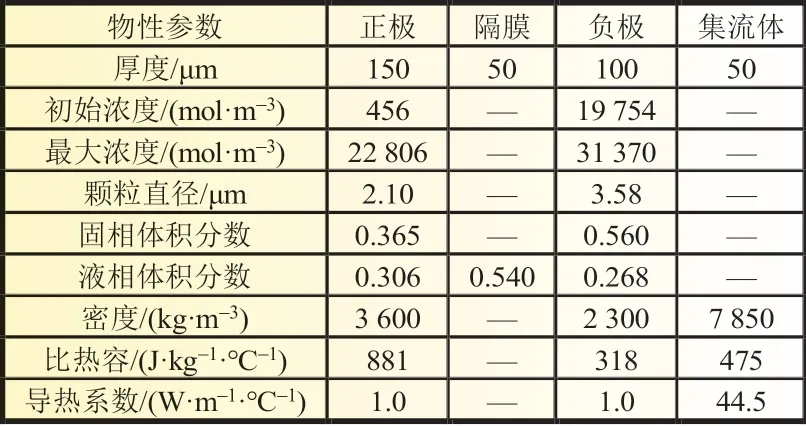
表1 双极性锂离子电池物性参数

1.4 模型验证

对于双极性锂离子热电耦合模型，其电化学反应对电池的生热特征影响最为重要，因此本研究将模型计算得出的电池放电曲线与文献[7]中结果进行对比，如图2 所示。可以看出，利用本文模型所得出数值结果与文献中的结果具有相同的趋势，其平均差异在5%以内，可以认为二者基本保持一致，因此证明了双极性锂离子电池热电模型的有效性。

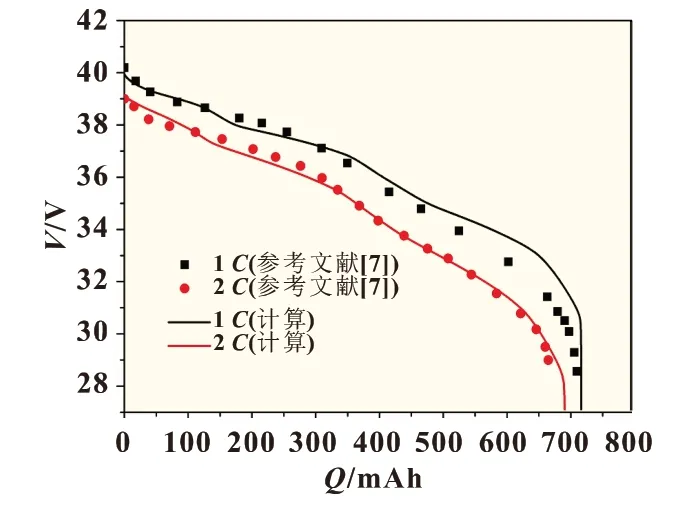
图2 模型有效性验证

2 结果与讨论

2.1 端面集流体结构对电池温度分布的影响

2.1.1 端面集流体厚度

图3 为具有不同厚度端面集流体的电池温度分布结果。由图可知，当端面集流体厚度与内部双极板相同时[图3(a)]，其极耳处的汇流生热效应十分显著，不但加热了附近的电池单元，而且造成电池中心出现大面积高温区域。随着集流体厚度的增加，集流体电阻减小，此时极耳附近的高温区域逐步缩小，并且电池内部温度最高的区域由端面电池单元转变为中心电池单元。磷酸铁锂/石墨体系电池使用温度不宜超过60 ℃[10]，最佳使用温度范围为0～45 ℃。然而在图4 结果中，自然散热条件下仅通过调整集流体厚度虽然可以降低最高温度及温差，但是无法使电池温度降至45 ℃以下。当端面集流体厚度为0.6 mm，可以满足最高温度小于50 ℃，最大温差小于5 ℃。但是，之后再进一步增加其厚度，温度分布改善效果则趋于平缓。因此，在对双极性锂离子电池端面集流体厚度进行设计时，应同时考虑电池温度分布的合理化与集流体的轻量化。

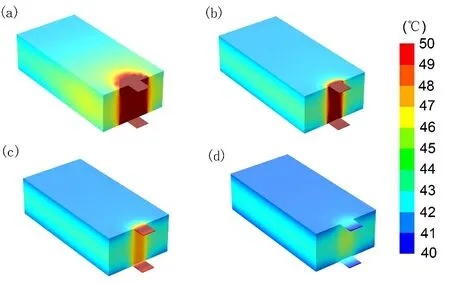
图3 具有不同厚度端面集流体的电池温度分布

图4 最高温度与温差随端面集流体厚度变化情况

2.1.2 端面极耳数量与位置

除了端面集流体厚度之外，电极片的长宽比与极耳结构也是影响电极片电流密度及温度分布的重要因素。但是，在研究中发现由于双极性锂离子电池结构限制，其电极片长宽比只能在小范围内进行调整，因而对温度特征的影响较小。所以，本文重点针对端面集流体的极耳数量与位置进行了研究。图5 为不同极耳数量与位置下最高温度与温差随时间的变化结果，所用集流体厚度为0.4 mm。从图中可以看出，采用双极耳和三极耳集流体可以大幅度降低电池的最高温度与温差，这是因为随着极耳数量的增加，汇流处的电流密度降低，导致焦耳热下降。与图4 结果相比，采用0.4 mm 集流体结合双极耳结构，其降温与均温效果要优于直接使用0.6 mm 集流体，同时还减轻了电池本体质量。另外，双极耳和三极耳的结果比较相近，说明双极耳条件下的汇流效应已经得到缓解，在此基础上继续增加极耳数量对降温的作用较小。在图5(b)结果中，三极耳条件下的温差在放电后期显著提高，其原因是放电后期电化学产热增加，此时产热较小的极耳就成为了散热通道，在降低极耳附近电池单元温度的同时，也导致了总体温差增加。此外，改变极耳位置也可以改善电池温度分布特征，正负极极耳异侧布置可以在一定程度上缓解热量在电池同侧集中，但是其效果对于该条件下的电池并不明显。

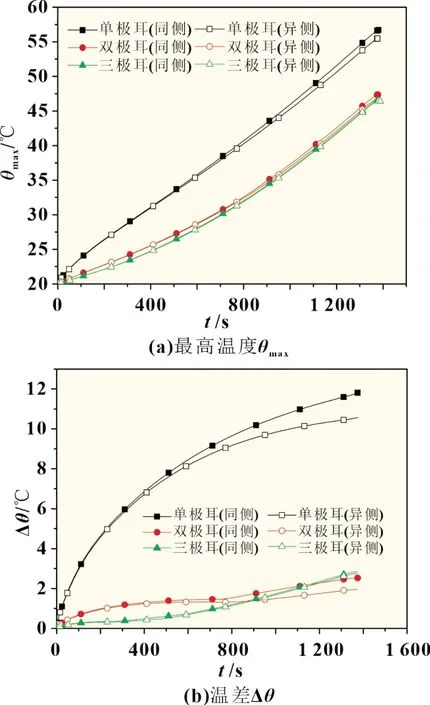
图5 不同极耳数量与位置下的最高温度与温差结果

2.1.3 等效汇流电阻

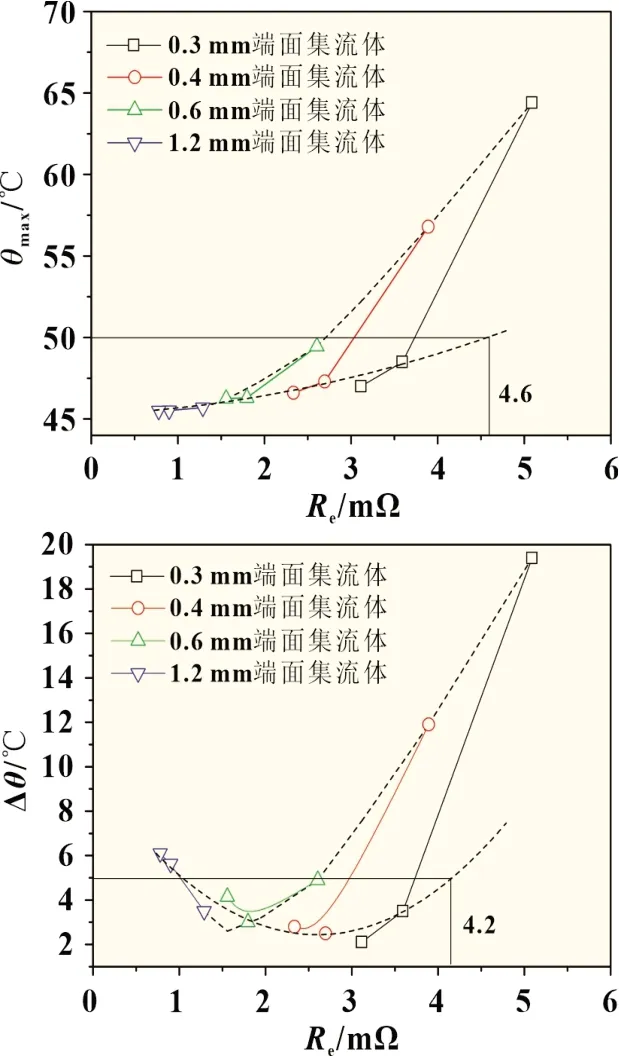
图6 最高温度(a)与温差(b)随等效电阻(Re)的变化情况

通过上述分析可知，优化端面集流体结构可以改善电池温度分布，但是两者之间呈非线性关系。因此，在考虑轻量化因素下，可能存在一种最优结构的集流体。为了探索该最优结构参数，可以计算不同集流体结构下的等效汇流电阻(Re)，其值为端面集流体电势差与总电流的比值。通过绘制Re与最高温度与温差之间的关系曲线(图6)，可以发现各种集流体结构方案构成了一个类三角区域，即图中虚线内部范围。该范围左边界为厚度变化结果，右边界为极耳数量变化结果。通过该图可以拟合出电池为实现特定温度条件所能承受的最大等效汇流内阻，从而指导集流体结构设计。比如在自然散热条件下，若要同时满足电池最高温度在50 ℃以下，温差在5 ℃之内，那么在本研究电极片尺寸下的端面等效汇流内阻应小于4.2 mΩ。因此，可以此参数为依据，综合厚度、极耳面积、数量、位置等参数，进一步完善集流体结构设计，从而获得该条件下的最优集流结构。

2.2 电芯传热过程与散热方式

2.2.1 电芯厚度

电芯作为电池在放电过程中的主要发热体，其厚度决定于双极性电池的额定电压设计，同时厚度又是影响电池温度分布的重要因素。图7 为自然散热条件下放电结束时不同电芯厚度的最高温度与温差结果(端面集流体0.4 mm，双极耳异侧分布)。最高温度随电芯厚度的增加先迅速升高，之后趋于平缓。但是，电池的最高温度始终保持在50 ℃以内，说明在汇流生热效应被弱化的情况下，电芯厚度对最高温度的影响有限。若要进一步降低电池温度，以达到电池最佳使用温度范围0～45 ℃以内，则需要将电池厚度控制在17 cm 以内。此外，自然对流下的电池温差均匀性较高，均不超过2.5 ℃。然而，电池温差随着电池厚度的增加呈现先降低后升高的趋势，这是由于当电池厚度较小时，仍会受到极耳处焦耳热的影响，由此导致了局部高温。而当厚度达到一定值时，电芯的电化学生热逐步成为电池温升的主导因素，并且大部分焦耳热能够被电芯所吸收，平衡了区域温度差异，导致此时的电池温差最低。当电芯厚度继续增加时，电化学产热量增加，热量聚集于中心电池单元从而引发了内外温差的继续增加。

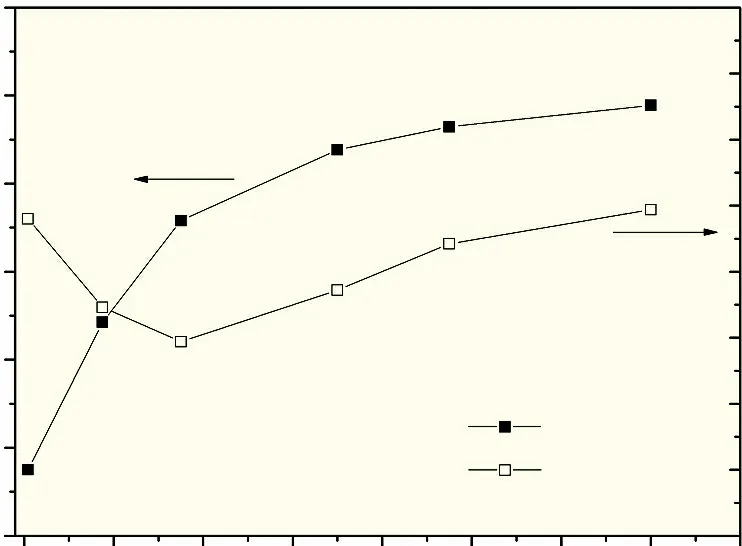
图7 放电结束时的最高温与温差随电芯厚度(d)的变化情况

2.2.2 散热方式

对于功率型双极性锂离子电池，采用强制散热方式是降低电池内部温度的有效手段。由于双极性锂离子电池四周为密封结构，因此端面集流体承担了主要散热功能。图8 为厚度是35 mm 双极性锂离子电池在不同对流换热系数(h)下的最高温度与温差结果(端面集流体0.4 mm，双极耳异侧分布)。从中可知，随着对流换热系数的提高，其最高温度逐步下降，而温差却不断上升。产生这一现象的原因主要是电芯的导热系数较低，导致中心电池单元的热响应速度较慢，无法与端面单元做到相对同步。为了保证电池最高温度低于45 ℃，最大温差不超过5 ℃，那么对于35 mm 厚度的电池其对流换热系数应在20～30 W/(m2·℃)，该数值范围内的冷却方式应为带有强制对流的空冷方式。

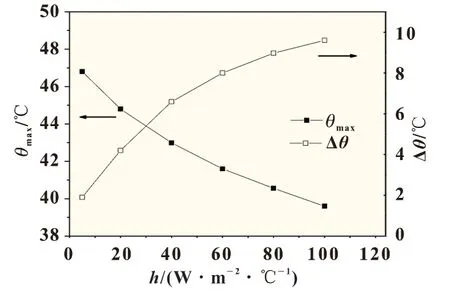
图8 放电结束时的最高温与温差随对流换热系数(h)的变化情况

2.2.3 电芯厚度与散热方式之间的关系

通过上述分析可知，为保证电池处于特定温度及温差范围内，调整电芯厚度与强化表面散热均可以作为有效的设计手段。为了综合分析电芯厚度与对流换热系数对电池热特征的影响，本文将不同电芯厚度在不同对流换热系数下的温度与温差临界值绘制在同一图中，如图9 所示。图中黑线的上部为最高温度小于45 ℃时的情况，而红线部分的下部为最大温差小于5 ℃的情况，两者的重合区域(抛面线部分)即为同时满足两种条件的参数范围。通过绘制h-d 关系图，首先能够确定在特定厚度条件下所应采用的散热条件，其次能够确定在电池所能承受的最大厚度及对应的对流换热系数。对于本文所设条件，电池的最大厚度应为40 mm，同时采用对流换热系数为25 W/(m2·℃)的强制空冷条件，才能够满足所需温度及温差范围。随着厚度的减小，所能采用的对流换热系数范围逐步扩大，由于对流换热系数的影响因素较多，所以在实际条件下不易精确控制。因此，在双极性锂离子电池设计过程中，应避免采用临界厚度的电芯尺寸，在满足输出电压等级的条件下适当减小厚度，从而减轻散热方式的设计压力。

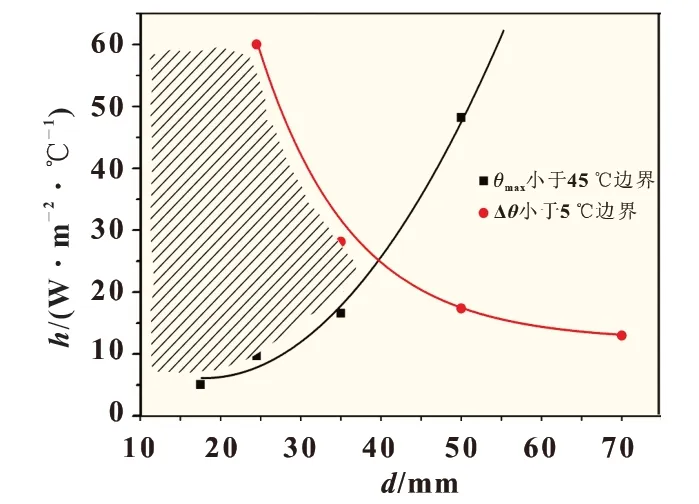
图9 满足特定温度范围内的对流换热系数(h)与电芯厚度(d)的关系

3 结论

本文通过建立双极性锂离子电池三维热电耦合模型，用于指导双极性锂离子电池热设计，重点研究了端面集流体结构、电芯尺寸及表面散热方式对电池温度特征的影响，主要结论如下：

(1) 端面集流体结构可以影响双极性锂离子电池的最高温度及出现位置，通过增加端面集流体厚度，可有效降低电池最高温度及温差；在本研究所述条件下，采用0.4 mm 集流体结合多极耳结构，其降温与均温效果要优于直接使用0.6 mm 集流体。

(2) 端面集流体厚度和极耳数量与电池最高温度和温差之间呈非线性关系，通过采用等效汇流电阻作为端面集流体设计的综合评价参数，可以对集流体结构进行优化。

(3)在自然散热条件下，电芯厚度的增加可以导致电池的最高温度上升，但是温差较小；采用强制散热条件有助于降低电池温度，但也使电池温差升高。

(4)通过绘制电芯尺寸与对流换热系数关系图，可以确定在本研究所述条件下，为满足最高温度及温差分别小于45 ℃与5 ℃条件，电池临界厚度及对流换热系数应分别为40 mm和25 W/(m2·℃)。