电热耦合模型与UKF组合估算电池温度与SOC

刘雨辰，周 飞，徐 帅，杨 文

(南京航空航天大学直升机传动技术国家级重点实验室，江苏南京210016)

以中小型无人旋翼直升机为代表的无人飞行器已经在现代战场和民用领域得到广泛应用，可替代人类在敌后战场、自然灾害、农业喷洒农药、新冠疫情等特殊场合执行各种各样艰难的任务，包括敌后精确战术打击、人员和灾情信息搜索和各类疫情的消杀等。然而，无人飞行器的动力系统是限制其战术用途、作战半径及续航里程的关键技术瓶颈。目前，锂离子电池因其具有高能量密度、高功率密度和无记忆效应等特点在汽车和中小型无人飞行器等领域得到了广泛的使用[1]。由于单人操作的无人飞行器要在不同高度和纬度环境下使用，因此锂离子电池的SOC 准确估算和适宜的工作温度是决定它能否正常工作的主要因素[2]。

目前用于估算电池温度和SOC 的模型主要有神经网络、电化学-热耦合模型和电热耦合模型。其中神经网络模型是一种黑盒模型，它不需要考虑电池的内部特性，当影响输出参数的训练数据越完整，估算结果越精确，但是对于锂离子电池来说温度和SOC 都是影响电池内部特性的重要因素，将他们同时作为输入参数会导致估算误差增大[3]。电化学-热耦合模型基于物料守恒和电荷守恒原理，综合考虑电池的电化学反应和传热描述了真实电池的电化学反应过程，从而实时获得电池的电动势和温升变化，但是这种方法需要求解多个复杂的非线性微分方程，不适宜用于电池管理系统中[4]。电热耦合模型将电池等效电路模型与热等效电路模型结合，其中等效电路模型用于模拟电池动态特性，利用等效电路模型的参数计算产热速率，热等效电路模型利用产热速率计算电池温度。Zhu 等建立了电热模型用于预测电池温度与SOC，但是其使用电流积分法计算电池SOC，且随温度的变化电池的容量未随着改变，在实际应用中温度的变化会导致初始SOC 误差，进而累积误差会使得SOC 估算误差逐渐地增大[5]。

针对目前电池模型和SOC 估算算法的不足，本文提出将电热耦合模型与无迹卡尔曼滤波法(unscented-Kalman filter,UKF)结合，可以在不使用热电偶测量电池表面温度的前提下，实时估算电池温度和SOC，将其用于调整模型参数，从而获得更高精度的估算结果。通过进行恒流放电和HPPC 工况实验，来验证电池温度和SOC 估算的准确性。

1 电池电热耦合模型建立与参数辨识

1.1 电池等效电路模型

锂离子电池在充放电时，其内部会发生复杂的电化学反应，在不同的时间尺度上具有不同的动态特性[6]，因此相比于一阶RC 等效电路，多阶RC 等效电路能够捕捉不同时间尺度上的电池动态特性，综合精确度和计算复杂度，本文选择了二阶等效电路模型，如图1 所示。Uocv为开路电压；U0为欧姆电阻电压；U1为第一个RC 电路的电压，表示极化电压；U2为第二个RC 电路的电压，表示浓度差电压。根据二阶等效电路和基尔霍夫定律，假设放电电流为正，得到电路方程如下：

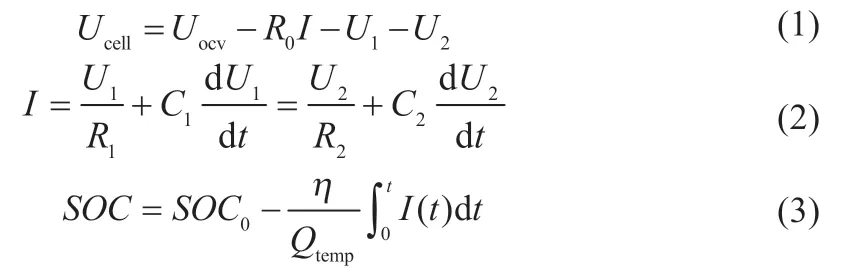
式中：SOC0为电池初始荷电状态；η 为库仑效率系数；Qtemp为电池容量，通过在不同温度下(-15、0、25、35 ℃)1 C 恒流放电实验得到，随温度的升高Qtemp逐渐增大；式中各阻抗数值主要与温度和SOC 有关。根据式(1)～(3)可以推导得到离散状态方程：

式中：Ts是采样时间间隔取1 s；[SOCkU1,kU2,k]T为状态变量；Ucell,k为测量变量；Ik为控制变量；[w1,kw2,kw3,k]T和vk分别为过程噪声和测量噪声，根据计算获得。

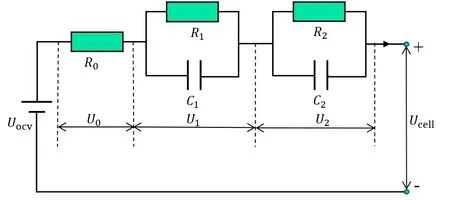
图1 锂离子电池的二阶等效电路模型

1.2 电池热等效电路模型

Chen 等研究表明，电池在恒流1.5 C 下放电，电池内部温度高于电池表面温度，表面温度和内部温度相差3 ℃，且表面温度相对内部温度滞后近200 s[4]。当电池在大电流工况或极端温度下，这种温度差异会变大。对于方形电池，可将极柱温度作为电池内部温度；但对于圆柱电池，因其结构问题，集流体温度不能代替电池内部温度，需要在制造电池时将热电偶嵌入电池内部测量电池温度，这极大地增加了制造成本[7]。Goutam 等研究发现电池温差主要是因为空气热对流导致电池表面温度较低，温度较低部分集中存在于电池表面，其质量占电池总比重较少[8]。因此将热量平均到整体电池上，进而建立的热等效电路模型所输出的温度，在理论上更加接近电池的真实温度。由于实际电池管理系统直接使用热电偶测量电池表面温度作为输入参数来估算SOC，一方面可能会因为热电偶测量的表面温度滞后于内部温度，从而内部温度提前达到热失控温度引发事故，另一方面在电池低温预热启动时，内部温度已经达到启动要求，而表面温度未达到，导致不必要的预热消耗和等待时间。为此，本文建立了如图2 所示的热等效电路模型用于预测电池温度。其数学表达式如下：

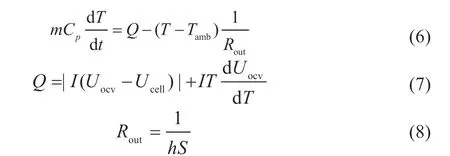
式中：m 为电池的质量；Cp为电池的比热容；Q 为电池产生的热量，主要由焦耳热和熵热构成；T 和Tamb分别为电池温度和环境温度；h 是热传递系数，其与电池面积的积的倒数视为热等效电路中的热阻；S 为电池表面积。

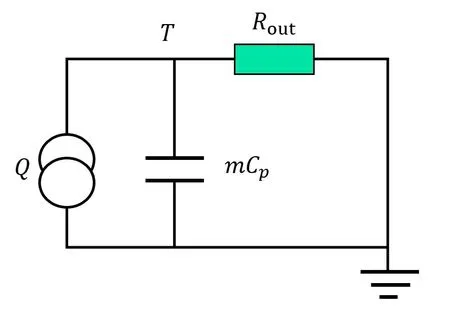
图2 电池的热等效电路模型图

1.3 电池的电热耦合模型的建立

图3 显示电池可以视为二阶等效电路和热等效电路的耦合。SOC 和温度用于实时调整模型参数，电池端电压Ucell和开路电压Uocv及其计算所得的电池热量Q 是模型耦合的桥梁，其中电池容量Qtemp随电池平均温度T 变化。电池开路电压Uocv及电池二阶等效电路中R0、R1、C1、R2、C2与温度T 和SOC 之间的关系，可通过在不同温度下HPPC 放电实验经过参数辨识获得，并通过实验测得电池的熵热系数dUocv/dT。

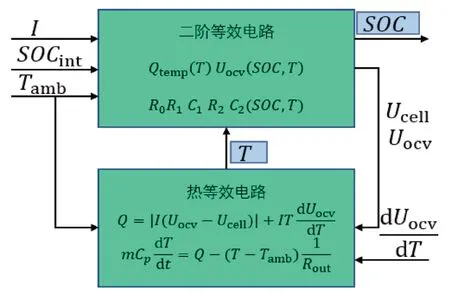
图3 电池的电热耦合模型流程图

1.4 参数辨识方法

先对式(4)和(5)推导差分方程，将HPPC 工况的放电电流和电压数据代入其差分方程，使用最小二乘法进行参数辨识。由于输入参数只有电压电流2 个参数，而对于二阶等效电路却要辨识5 个参数，其结果可以有无数解。虽然这样的结果依然可以用于估算电池SOC，但是不能用于电池产热量的计算。为了解决这个问题通常需要耗费大量时间调整参数，因此利用MATLAB/Simulink-simscape 建立用于参数识别的二阶等效电路模型(图4)。将电池分别在-15、0、25、35 ℃的HPPC 工况下测得的电流和电压数据用于离线参数识别，再将得到的参数代入模型中用于电池产热量的计算。

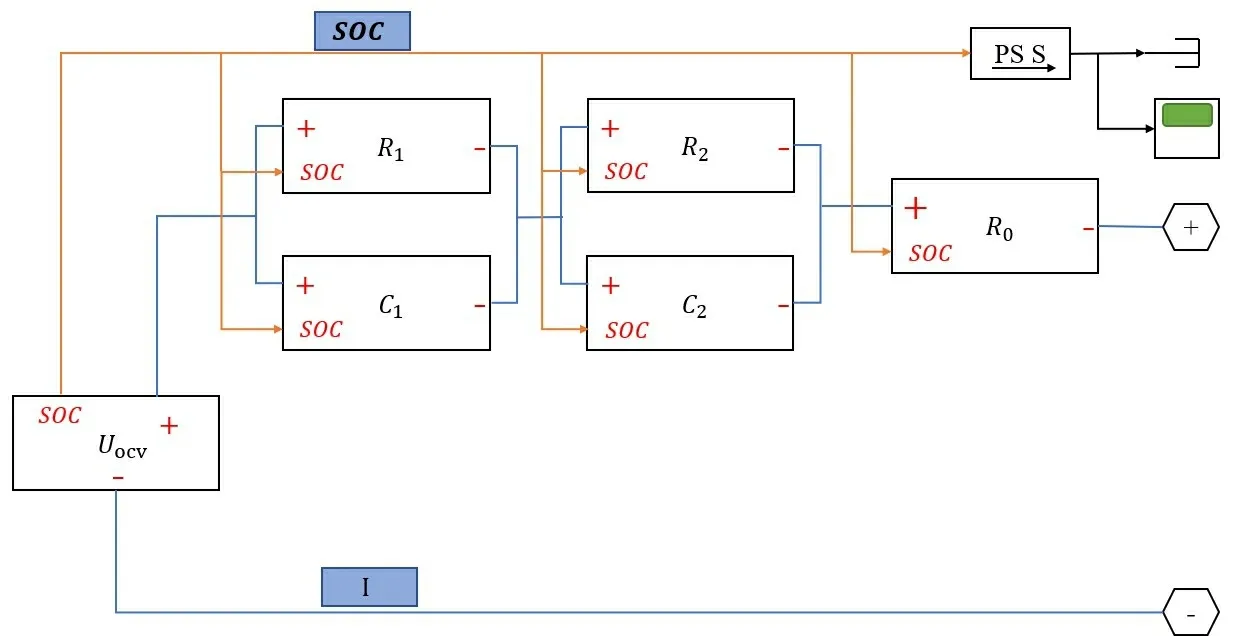
图4 Simulink 中搭建用于参数识别的二阶等效电路模型

2 UKF 与电热耦合模型组合估算电池SOC 和平均温度

2.1 UKF 估算原理

无迹卡尔曼滤波(UKF)算法是卡尔曼滤波法与无损变换(unscented transform, UT)的结合，将卡尔曼滤波器中对下一时刻的预测变为对sigma 点集的扩充并进行非线性映射，既避免了雅克比矩阵的计算，又可以很好地适应非线性系统。下面描述了UKF 算法计算流程。

(1)初始化：

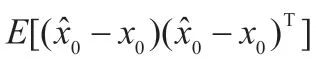
(2)构造2L+1 个sigma 点，L 为状态向量维度：

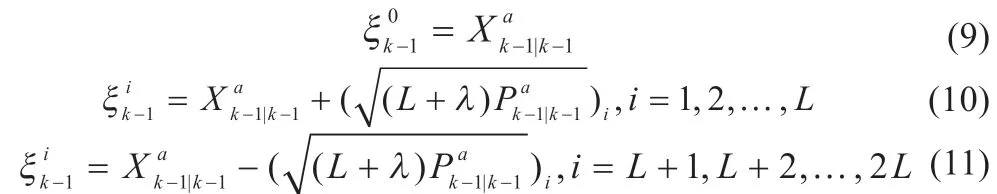
(3)通过状态方程将sigma 点集映射到新的sigma 点集上：

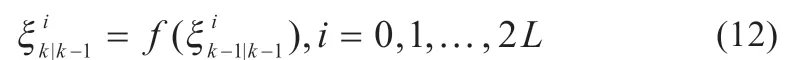
(4)新的sigma 点集经过加权后得到预测状态向量估计值和协方差：

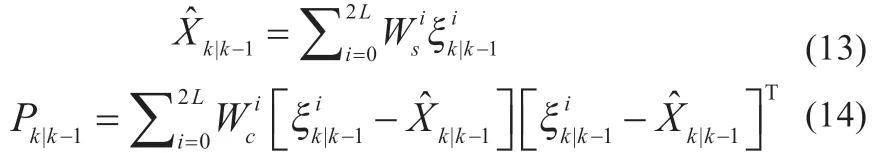
其中，权重公式：

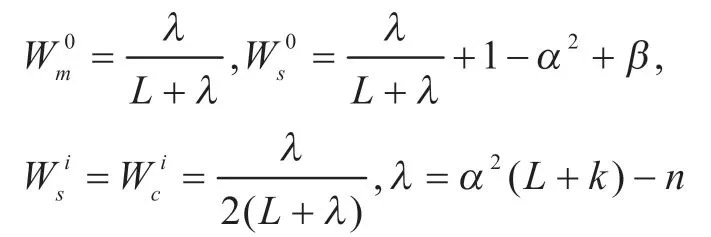
(5)通过观测方程将sigma 点集映射到新的sigma 点集上：

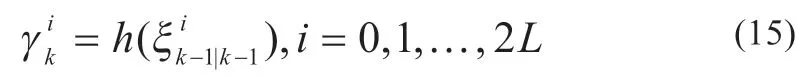
(6)将加权得到的新的sigma 点集用于预测观测的估计值和协方差：

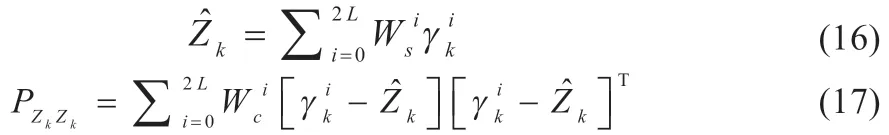
(7)将状态测量的协方差矩阵用于计算UKF 的卡尔曼增益：

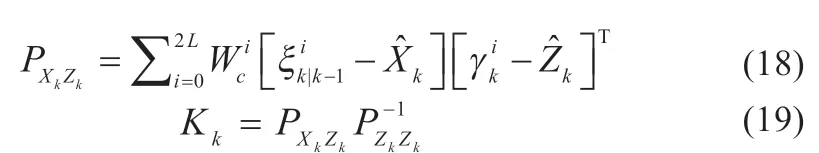
(8)滤波更新：

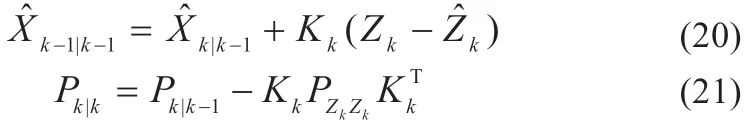
2.2 UKF 与电热耦合模型组合算法估算电池SOC 及其平均温度

图5 显示电热耦合模型与UKF 结合算法。首先使用初始SOCint、环境温度Tamb来设置二阶等效电路模型，并根据输入电流I 来计算模型端电压Ucell。以模型端电压Ucell，实际端电压U 和电流I 作为UKF 的输入参数来估算电池实时SOC。以模型端电压Ucell，实际端电压U 和环境温度Tamb作为热等效电路的输入参数来估算电池平均温度T。最后使用电池平均温度T 和UKF 估算的SOC 在线调整该模型参数Qtemp, R0, R1,C1,R2,C2。

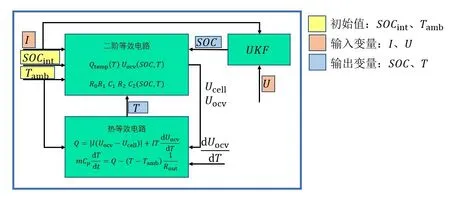
图5 UKF与电热耦合模型结合算法流程图

3 模型标定与实验验证

3.1 实验方法

以长虹三杰18650 动力锂离子电池为研究对象，其主要参数如表1 所示。本次实验平台设备主要包括新威高精度锂离子电池测试系统、高低温箱、温度记录仪和工控机，其内部联系见图6。

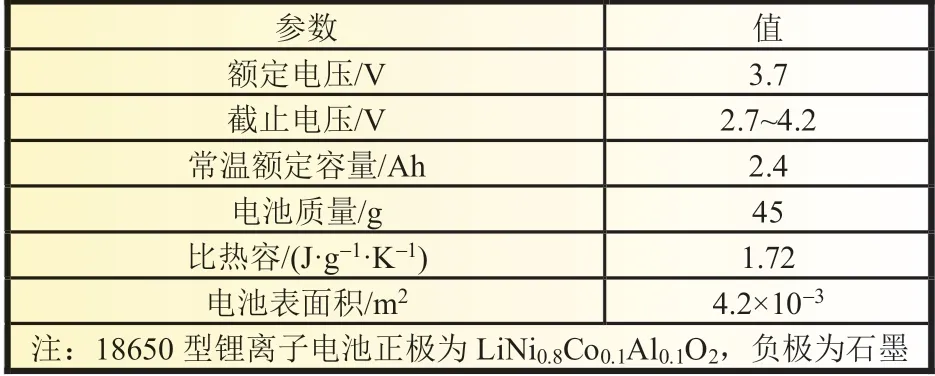
表1 实验用18650 型锂离子电池参数

首先在高低温箱进行电池熵热系数测量实验，然后在-15、0、25、35 ℃温度下进行了1 C 恒流放电和HPPC 工况放电实验，将以上实验数据用于标定上述模型参数。在常温下进行1 C 恒流放电实验，通过对比实际电池的放电电压和温度与模型估算结果的差异，来验证热等效电路模型精度。然后在常温下对电池进行NEDC 工况放电实验，将电池实际的输出电压、温度和SOC 与模型的估算结果对比，来验证电热耦合模型与UKF 组合算法的精确度。

HPPC 工况需要首先将电池充满电直到充电截止电压4.2 V，静置2 h 后，然后依次循环以下步骤，2 C 脉冲放电10 s，静 置40 s，2 C 脉 冲 充 电10 s，静 置40 s，1 C 恒 流 放 电10%SOC，静置1 h，直到电池达到放电截止电压2.7 V。NEDC 工况是欧洲对纯电动车续航能力的综合测试标准，它包含4 个市区循环和1 个郊区循环。图7 所示为NEDC 工况的电流与时间曲线。首先以1 C 电流对电池充电，随后静置1 h，接着按照5 个NEDC 工况进行放电，用于测试电池的SOC 估算精度。

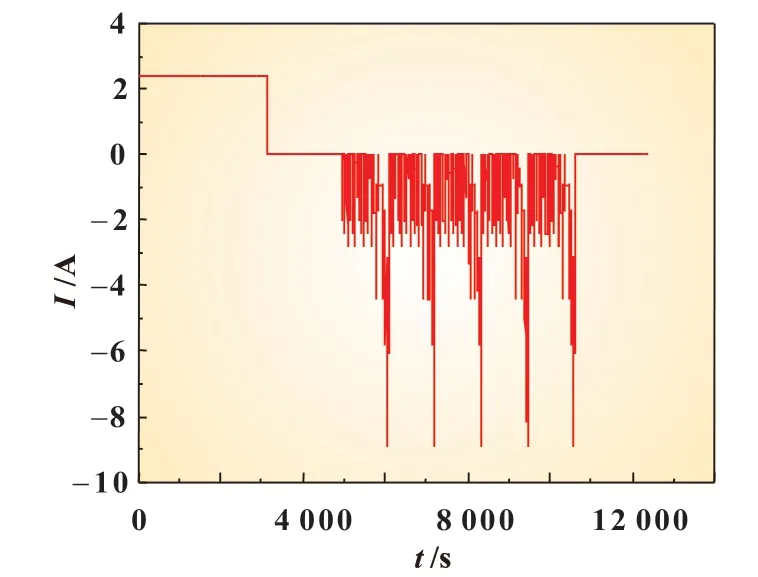
图7 NEDC工况电流变化曲线

3.2 标定模型参数

根据本实验室以前研究成果[9]，该电池的熵热系数和SOC 的关系见图8(a)。利用三阶多项式拟合，结果见式(22)，拟合残差为0.006 31。在不同温度1 C 恒流放电测试中，通过设置电池电流大小使电池恒流放电时间为1 h，由此得到电池在该温度下的总放电容量。图8(b)显示四个温度下电池的额定容量，通过二阶多项式拟合，可以得到电池容量与温度的函数关系,见式(23)，其拟合残差为5.3×10-6。

熵热系数：

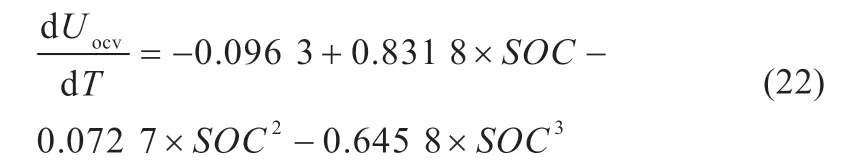
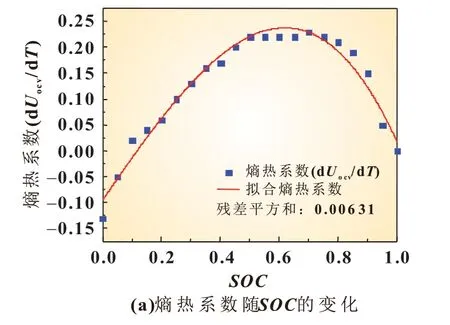
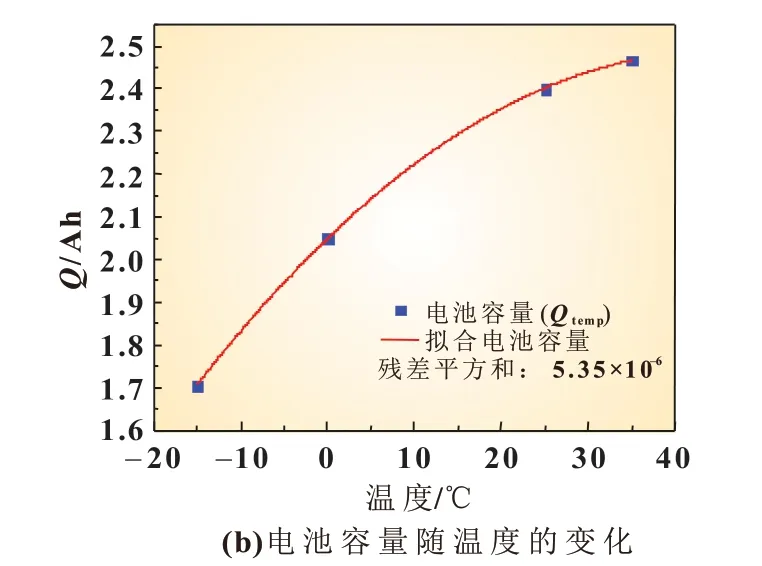
图8 电池的额定容量和熵热系数

电池容量：

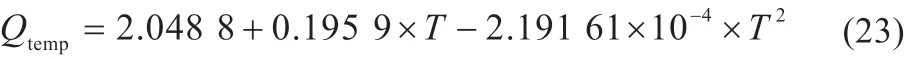
将不同温度下HPPC 实验数据代入Simulink 模型中进行参数辨识。图9(a)为电池在25 ℃条件下的HPPC 放电电压曲线和模型输出电压；图9(b)为模型仿真值与真实电压值的误差曲线图。模型输出电压值与真实电压值的误差均方根(root mean square error, RMSE)约为0.006 7 V。根据误差和RMSE 判断，模型精确度高，二阶等效电路中辨识参数的可信度高。图10 为不同温度下的等效电路参数变化曲线。由图10(a)可知，随温度的降低相同SOC 对应的开路电压逐渐升高。图10(b)和(c)反应了电池的动态特性，随温度的降低逐渐减小，这是由于温度降低锂离子扩散系数降低，反应速度变慢导致的。由图10(d)～(f)可知电阻受温度影响较大，随温度降低，电阻逐渐增大且在0 ℃以下变化最为明显，电阻在相同温度下随SOC 的降低变化不明显，只有当SOC 接近0 时才会出现较大增长。

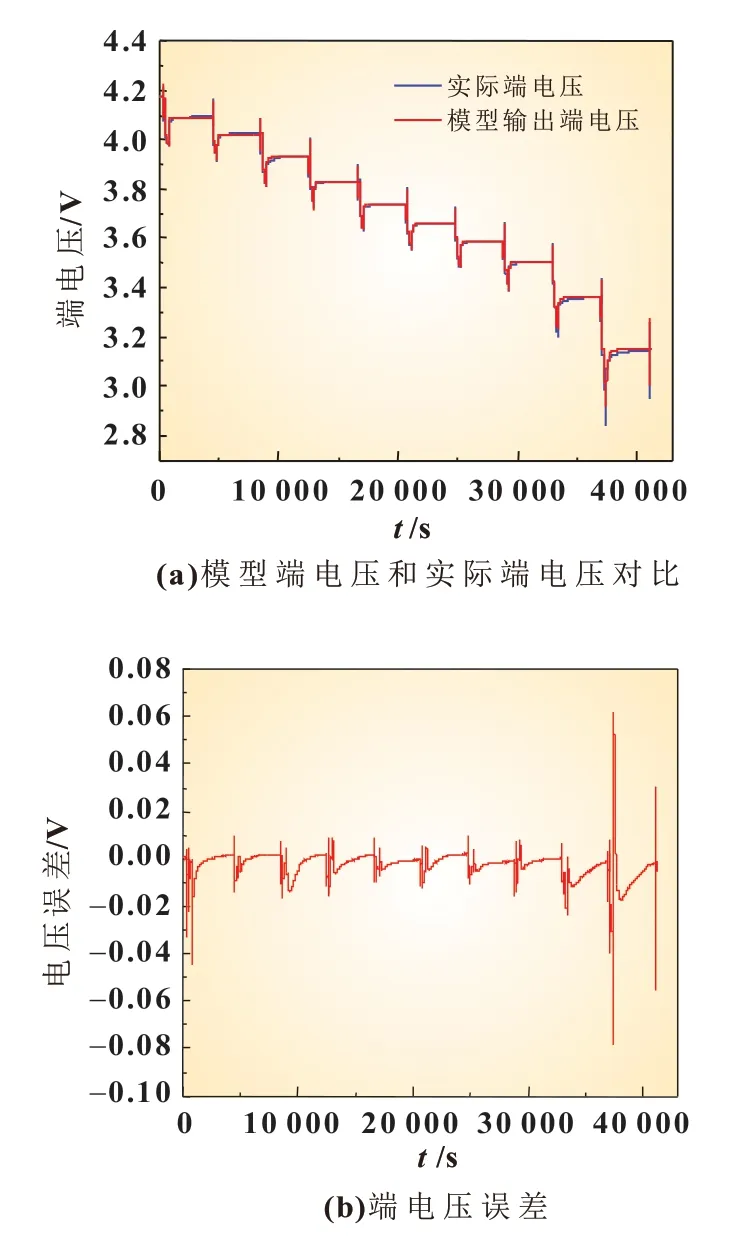
图9 HPPC 工况模型验证

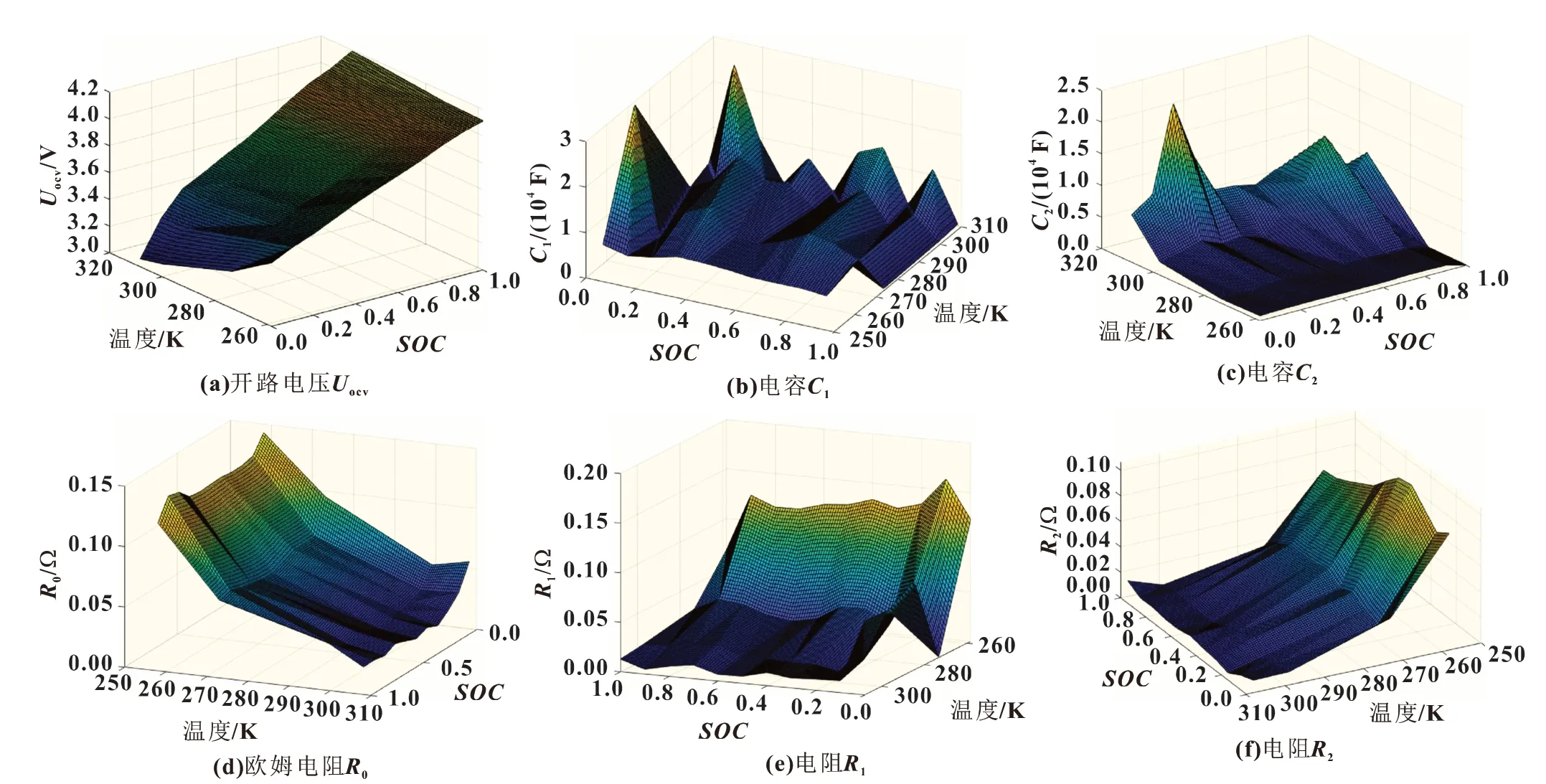
图10 参数识别结果随SOC及温度的变化

3.3 电池在恒流放电工况的温度与电压估算

图11(a)为模型估算温度与电池表面温度随时间的变化曲线。由此可见，它们的变化趋势相同，但随着放电时间延长，模型估算温度高于电池的表面温度，且温度误差逐渐增大，最大温差为1.5 ℃[图11(b)]。这是由于电池表面的金属外壳随温度升高电导率逐渐降低。由式(8)可知，电池表面与空气的对流换热系数减小，使得内部热量逐渐积聚，导致电池温差增大，因此热电偶测量的表面温度不能代表电池实际平均温度，而模型输出的平均温度更加可靠。从图11(c)和(d)所示，恒流放电工况下电压误差在0.04 V 内，RMSE 为0.010 7，这说明该模型在恒流放电工况下具有高精确性。

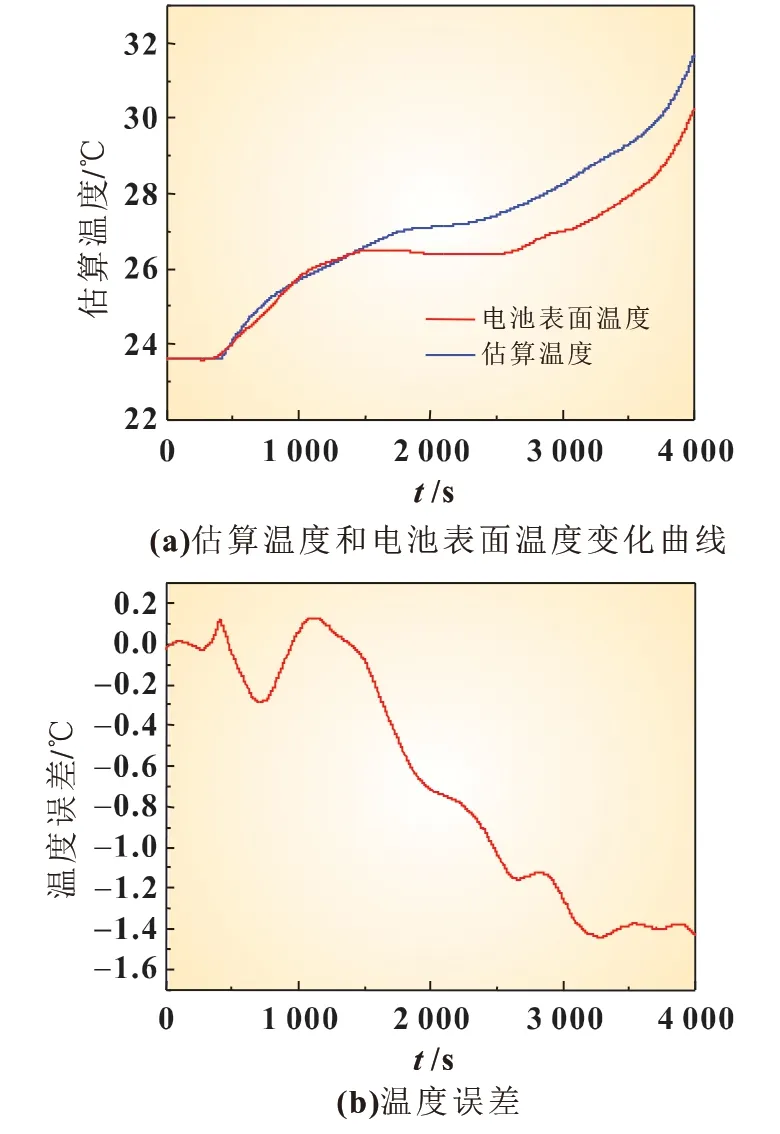
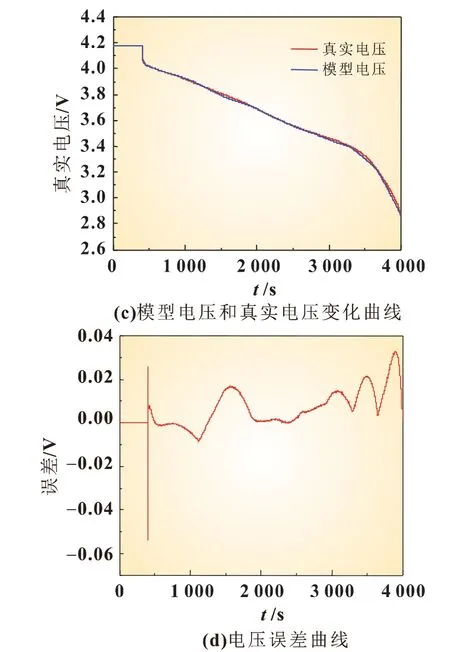
图11 1 C恒流放电模型温度响应与电压响应

3.4 电池在NEDC 工况下的温度与电压估算

图12(a)为NEDC 工况下电池模型的动态电压响应曲线与真实电压曲线，根据图12(b)可知，电压误差在-0.05～0.20 V内，且均方根误差(RMSE)为0.022 2。图12(c)和(d)中模型温度与电池表面温度曲线变化趋势相同，模型估算温度高于电池真实表面温度。在恒流充电阶段末期出现最大温差为2.6 ℃。

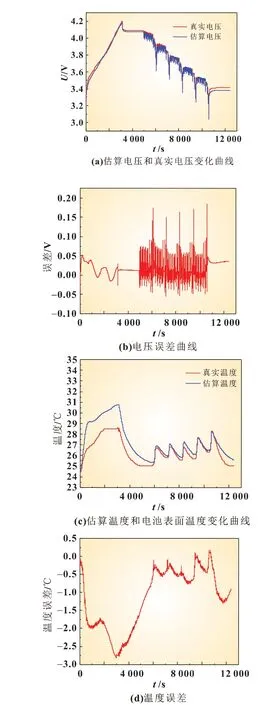
图12 混合工况下模型温度响应与电压响应

图13(a)是常温下NEDC 工况的真实SOC 与估算SOC 曲线。假设估算SOC 值都为0，与真实SOC 相同。从图13(b)可见，SOC 的估算误差保持在1%以内，其RMSE 为0.007。

3.5 SOC 估算收敛性

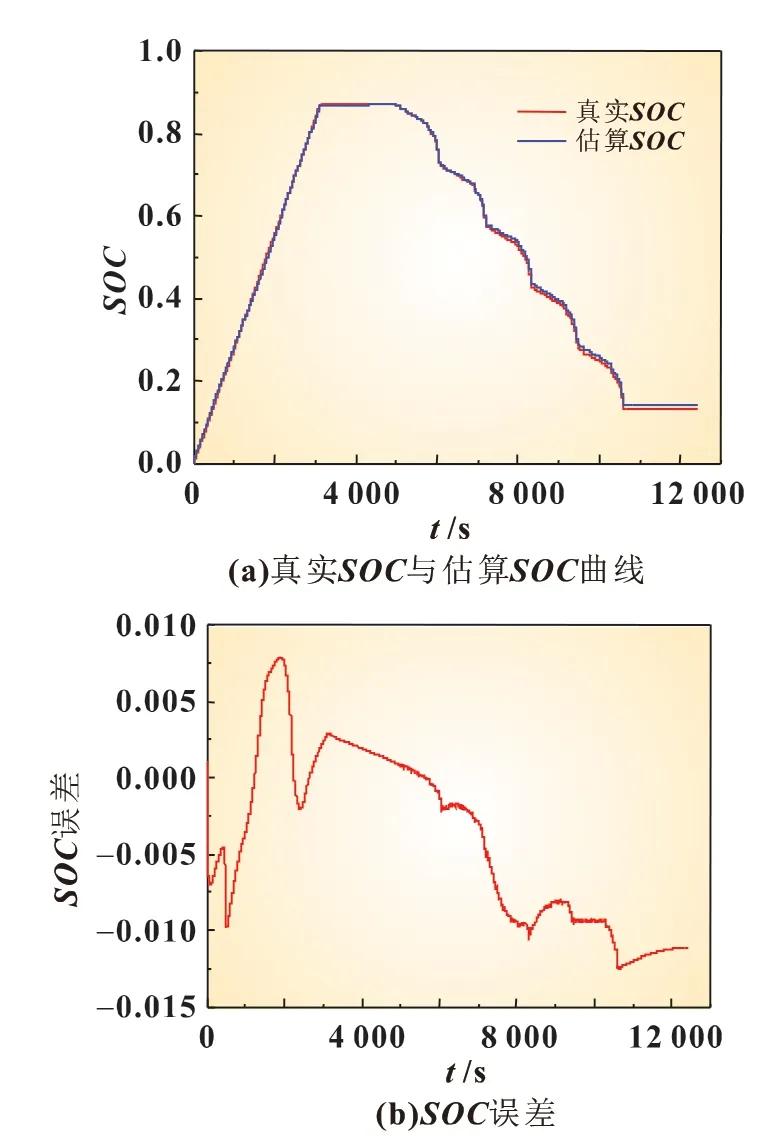
图13 常温下混合工况SOC估算

为了验证SOC 收敛性，首先将电池在常温下以1 C 电流充电至截至电压4.2 V，记录电池初始SOC，静置2 h 后，完成5 个NEDC 工况，通过设置与真实SOC 不同的估算SOC 初始值，观察算法能否收敛到真实值。本实验在常温下使用1 C电流为额定容量的2.4 Ah 的电池充电，由于没有恒压充电阶段，电池到达截止电压4.2 V 后结束充电，记录充电电量为2.1 Ah，即电池真实SOC 为87.5%，静置2 h 后，进行NEDC 工况循环，设置估算SOC 初始值为50%、60%、100%，其结果如图14(a)所示。当给定的初始SOC 与真实SOC 存在较大差异时，使用本文提出的估算方法依然可以快速跟踪到真实SOC，具有很高的估算精度。从图14(b)可知，当时间经过250 s 后，SOC 收敛到2%以内，显示该算法具有很好的收敛速度。

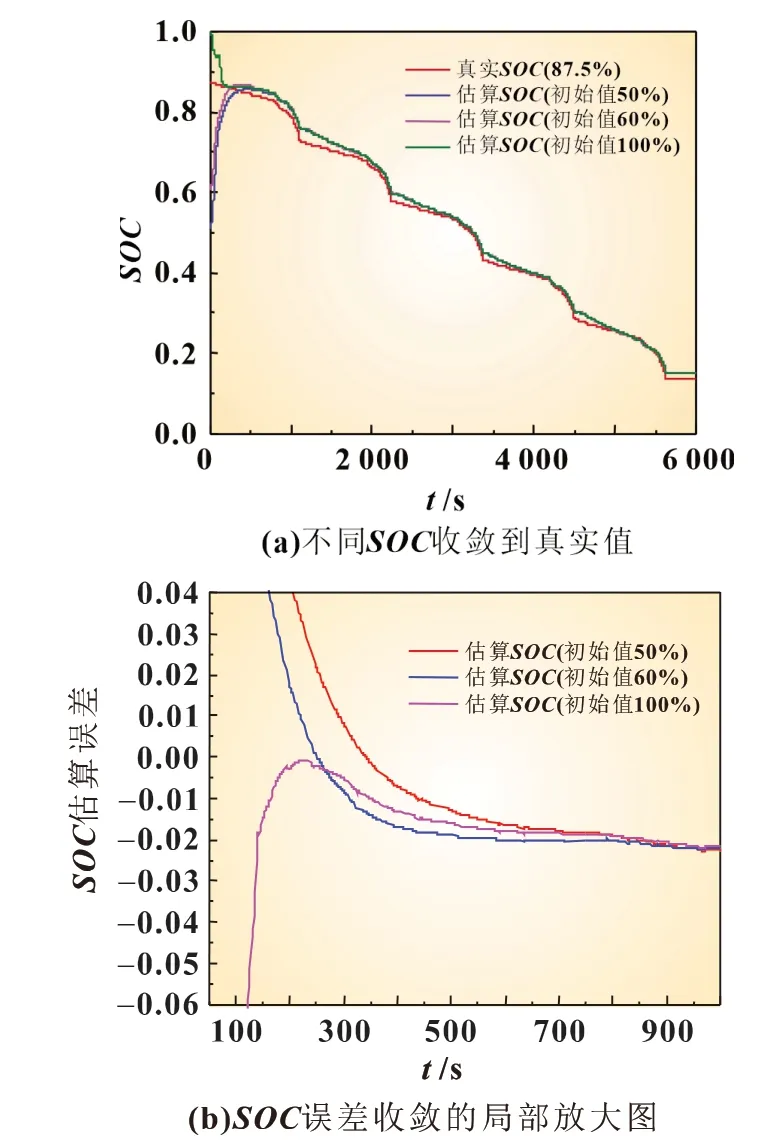
图14 SOC收敛性

4 结论

(1) 提出了电热耦合模型与UKF 组合算法来估算电池平均温度和SOC。根据电池电压电流和环境温度估算电池平均温度，并且将平均温度作为电池SOC 估算的输入参数，当初始值足够精确，SOC 估算误差在1%以内。

(2)估算平均温度与电池表面温度具有很好的跟随特性，估算平均温度虽然略高于热电偶测量的表面温度，最大温度误差为2.4 ℃，满足估算平均温度的精确度要求。

(3)在实际SOC 为87.5%的情况下，设置不同估算SOC 初始值(50%、60%、100%)，算法均能在250 s 内将误差收敛到2%以内，因此具有高估算精度和良好的收敛速度。