适用于山地城市的Logistics速度-密度模型
周约珥, 龚华凤*, 赵聪霄, 黄博亚, 徐小童
(1.林同棪国际工程咨询(中国)有限公司, 重庆 401121; 2.重庆市山地城市可持续交通工程技术研究中心, 重庆 401121)
由于特殊地形条件,山地城市普遍存在主干道上设置低等级互通立交的情况,且相关技术手册[1]缺少对低等级立交基本段通行能力的研究,导致了道路设计与交通运行不匹配等一系列问题。为了解山地城市的连续交通流特性,逐步解决上述问题,作为通行能力理论基础的交通流要素关系模型不可或缺。
通常,交通流要素关系模型可分为速度-密度模型与速度-流量模型。其中,速度-密度模型是Greenshields为间接计算道路通行能力而首先提出的,但其模型的适用范围有限,仅适用于中等交通密度的交通流[2],与之类似的模型还有仅适用于高交通密度的Greenberg模型[3],以及仅适用于低交通密度的Underwood模型[2]。相对于上述模型,作为分段模型的Edie模型[4]可适用于不同的交密度条件,但该模型中的部分参数物理意义不明,不具备可复制性。除了适用条件的约束与模型参数的物理意义不明,模型表达式复杂等问题也普遍存在于类似的速度-密度模型研究中[5-9]。相对而言,基于速度-流量的关系模型可直接确定道路的最大通行能力[10-14]。但该类模型的参数多为经验值,物理意义不明,欠缺客观性,如由美国联邦公路局(bureau of public road, BPR)函数演化而来的Nielsen模型[10]。此外,在高密度交通流条件下,速度-流量的数据散点一般呈放射发散分布,导致该类模型的拟合效果欠佳,计算结果难以趋于稳定。因此,在一般研究中,基于速度-密度的关系模型表现更优。
针对速度-密度关系模型,Macnicholas[15]认为理想的速度-密度模型应具备不分段、边界明确、适用于不同的交通密度条件、表达式简单、参数物理意义明确等特点。目前,仅基于Logistics的速度-密度模型比较符合Macnicholas[15]标准。该类模型原是计量化学模型[16],后被Wang等[17]用于交通领域研究,取得了十分理想的拟合结果。但Wang等[17]采用的五参数Logistics模型,未就实际交通运营规律做相应调整,导致部分模型参数的物理意义不明。为此,马晓龙等[18]基于Logistics的基本理论,提出了新的Logistics速度-密度模型,并根据实测数据对模型进行了验证与分析。但在马晓龙等[18]的研究中,速度上界与自由流速度的关系模糊,难以在实际应用中对两者进行界定。因而目前基于Logistics的速度-密度关系模型的研究,还有进一步的优化空间。
综上,针对速度-密度模型的研究还存在以下问题:①早期模型的应用范围有限,难以应用于交通密度复杂多变的山地城市;②多数模型参数的物理意义模糊,且不具备可复制性;③部分模型的表达式复杂,参数标定困难等。为解决上述问题,本研究以Logistics理论为基础,根据实际交通流运行的特点,推导了关键交通流参数之间的关系,从而建立了各参数物理意义明确,模型表达式简单,且符合一般交通流运营规律的Logistics速度-密度模型。最后,本研究基于重庆市的交通数据,对模型在山地城市中的适用性进行了验证与分析。
1 Logistics模型
Logistics的本质是描述自变量与因变量变化速率关系的微分方程。在交通研究背景下,Logistics模型的微分方程表达式为
dv/dk=Rv(k)
(1)
式(1)中:v为速度;k为密度;R为速度变化率函数。根据等号左侧的表达式可知,R的量纲为交通密度量纲的倒数。
速度、密度、流量两两相关是一般交通流的基本特性。结合实际交通流运行特点可知,交通速度必然是随交通密度的增加而降低。因此,基于Verhulst的阻滞增长假设,假定速度变化率函数R为一元函数,在密度变化的区间内,R的表达式为
R=rk(k/kf-1)
(2)
式(2)中:rk为速度变化率常数,与道路条件相关,量纲同R。由一般的速度-密度关系可知,该参数应为负数;kf为维持自由流状态的最大密度,理论上该值趋近于0。而在HighwayCapacityManual[1]中,kf可通过自由流速度与维持自由流状态的最大流量,间接计算获得。
综上,自变量与因变量变化率的关系、一般交通流特性中的速度-密度关系是建立Logistics速度-密度关系模型的基础。如何将上述两种关系有机结合,是模型成败的关键。
2 速度-密度模型的建立
2.1 模型基本表达式
基于对Logistics模型理论的分析,可对式(1)微分方程求解得到速度-密度模型的基本关系式为
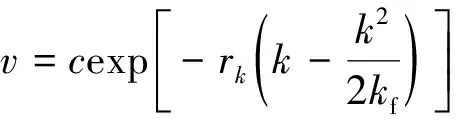
(3)
式(3)中:c为求解微分方程时产生的常数。根据交通流的边界条件可知,当密度k=0时,应存在v=vf,其中vf为自由流速度。式(3)可改写为

(4)
式(4)中:速度变化率常数(rk)仍存在物理意义不明的问题。为此,本研究对速度-密度模型的基本关系式进行了分析与讨论,以明确速度变化率常数(rk)的物理意义。
2.2 速度变化率常数
基于Logistics曲线的几何特征,对速度变化率常数与其他参数间的关系进行了相关推导,从而通过参数消元,优化了速度-密度模型基本关系式,进而分析了模型边界的合理性。
基于速度的物理意义可知,速度-密度模型基本关系式的一阶导数为加速度,二阶导数为加速度变化率。考虑到Logistics模型的函数为平面S形,存在拐点(kt,vt),使得v″=0。因此,速度-密度模型基本关系式的特点可归纳如下。
(1)速度-密度基本关系式的一阶导数(加速度)始终存在v′≤0。当v′=0时为自由流状态或绝对拥堵状态。
(2)在速度二阶导数为0的拐点处,加速度变化率由负转正。
由各阶导数间的关系与交通流的特性可知,Logistics 曲线中的拐点同时存在3种身份:①该点是Logistics曲线的几何拐点;②该点是速度一阶导数的极值点;③在速度-密度关系中,该点是标志着交通流由稳定流向拥堵流转变的关键点,其对应的交通流量为最大通行能力。因此,拐点(kt,vt)处的交通流密度又称为最佳交通密度(km),交通流速度又称为最佳交通速度(vm)。
关于拐点的数学描述可归纳为

(5)
对式(5)进行求解,得到速度变化率常数(rk)、最佳交通密度(km)及维持自由流状态的最大密度(kf)三者间的关系式为

(6)
由式(6)可知,当且仅当rk<0时,式(6)成立,且此时的rk符合交通流运行的一般规律。通过参数消元,式(4)的速度-密度关系模型可进一步改写为
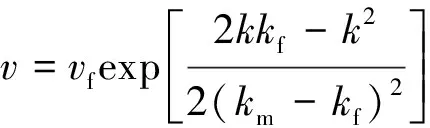
(7)
该模型具有参数物理意义明确、表达式简洁等特点,但仍需进一步分析模型的数学边界,以确定模型的合理性。
2.3 速度-密度关系模型的边界
基于Logistics的速度-密度关系模型的一阶导数为

(8)

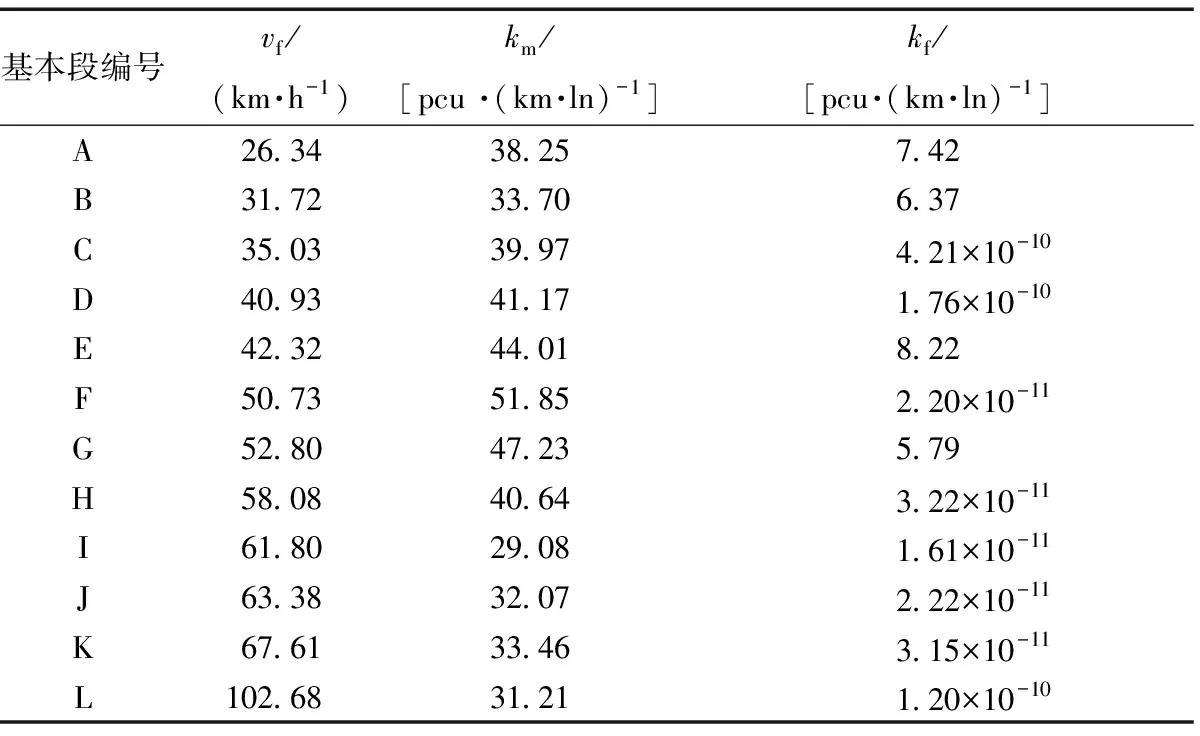
综上,在k∈[0,kf)区间内,Logistics曲线近似于平行k轴的水平线,v≈vf恒成立;在k∈[kf,)区间内,0 为验证模型在山地城市的适用性,基于重庆市的实测交通流数据对模型进行了验证分析。数据通过固定检测器、视频记录采集。其中,固定检测器的数据采集间隔为1 min,是由断面流量、单点速度组成的全天交通流数据。密度可通过流量、速度与密度的一般关系式计算获得;视频记录数据作为补充部分,调查了部分立交基本段的早晚高峰期情况。调查时间为8~10月份。调查范围涵盖了重庆市渝中、渝北等7区14座互通立交,合计36个互通立交基本段的有效数据。样本涉及了各级道路与不同的运行速度水平,其中主线23条、匝道13条,各基本段的限制速度介于25~100 km/h不等。 选取12条不同等级、不同限制速度、不同交通条件的互通立交基本段作为模型验证的案例,基本涵盖了重庆市各等级道路。各基本段模型的标定均基于1stOpt软件平台完成,标定所得的主要模型参数结果如表1所示。 在表1中,仅自由流速度vf是实际调查获得,最佳交通密度(km)与维持自由流的最大密度(kf)均为1stOpt输出的标定结果。 基于表1结果,计算了最佳交通密度(km)的平均值、中位数以及标准差,分别为38.55、39.11、6.94 pcu/(km·ln)。而在HighwayCapacityMa-nual[1]中,连续流最佳交通密度建议值为 28 pcu/(km·ln),显著低于山地城市的实测平均值与中位数。此外,标定获得的最佳交通密度(km)离散程度较小,可能存在一个最佳交通密度(km)的标准值适用于各类连续交通流。 为进一步验证模型在山地城市复杂交通条件下的适用性,研究对比了模型与各基本段实测数据的拟合情况,如图1所示。由拟合结果可知,所建立的模型在不同交通流条件下,均取得了较好的拟合效果,最小拟合优度为0.41,最大拟合优度则高达0.94,平均拟合优度为0.79,拟合优度的中位数为0.84。 表1 各互通立交基本段参数标定结果 图1 基本段A~L的模型拟合结果Fig.1 Data fitting results of basic segment from A to L 如图1(c)、图1(e)、图1(g)、图1(i)所示的基本段拟合结果,针对数据质量高,且交通流密度变化范围较大的路段,模型具有极高的拟合优度,为0.84~0.94,能较好地反映不同交通密度条件下的速度-密度关系。 图1(d)、图1(f)、图1(i)所示的基本段数据质量与拟合优度均依次升高。该结果表明针对交通流密度变化范围较大的路段,采集数据的质量越好,模型的拟合优度越高。 图1(k)、图1(h)、图1(g)、图1(i)所示的各基本段样本数据的交通流密度变化由小到大依次排列,且模型拟合优度依次升高。该结果表明针对数据质量较好的路段,交通流密度的变化范围越大,模型的使用效果越好。 如图1(h)、图1(k)所示的案例基本段拟合结果,针对数据质量较好,但交通流密度变化范围较小,仅存在自由流状态的路段,模型仍可根据既有的交通数据拟合得到相对合理的最佳交通密度km,但拟合优度明显偏低。 综上所述,所建立的Logistics速度-密度关系模型适用于不同交通密度条件下的交通流。但模型的拟合精度与采集数据的质量、路段交通密度的变化范围密切相关。 为验证模型的优越性,研究选取路段F数据,对比了不同模型拟合结果,该路段数据覆盖了不同的交通密度条件,能充分验证不同模型的拟合优劣。结果如表2所示。 表2 不同模型拟合结果对比 基于各模型的对比结果(表2)可知,在文献[17]模型的结果中,θ1、θ2为无物理意义的参数,且密度无穷大时,拥挤速度不为0,与实际交通运行规律相悖。在文献[18]模型的结果中,拥挤速度与实际交通相符,但拥挤密度、最大交通速度(Vmax)却远超正常值。在本模型结果中,km与城市道路工程设计标准的建议值基本一致,kj则趋近于0,与交通运行规律与模型假设契合。综上结果可知,在拟合优度基本一致的条件下,本研究模型的拟合参数较少,且各参数拟合结果符合一般交通运行规律,更具实用价值。 针对山地城市的复杂交通条件,建立了基于Logistics的速度-密度关系模型,并得出如下结论。 (1)模型的表达式简单,且各参数的物理意义明确,符合连续交通流运行的一般规律。 (2)针对模型中的主要标定参数,山地城市道路的最佳交通密度要明显高于HCM提供的建议值,平均最佳交通密度为38.55 pcu/(km·ln)。 (3)模型适用于各类交通密度条件,最高拟合优度可高达0.94。尽管模型的拟合优度受数据质量、交通流密度变化范围等制约,但其拟合结果仍具有较强的借鉴意义,尤其针对仅存在自由流状态的道路,本文模型仍可标定相对合理的模型参数。3 模型验证
3.1 数据采集
3.2 拟合分析

3.3 中外同类模型对比分析

4 结论
——拟合优度检验与SAS实现

