基于集成学习的交通流短时特性分析与神经网络预测方法
郑乐军, 文成林
(杭州电子科技大学系统控制工程科学研究所, 杭州 310018)
城市交通控制系统的作用是对城市路网中的交通流进行合理控制,使其分时使用交叉路口,避免发生交通事故、缓和或防止交通拥塞并及时为车辆上的有关人员及行人提供交通状况信息以增进交通安全性。为了实现这种控制,系统需要对实时交通状况有即时的了解,同一种预测方法在不同时间段和地段交通流预测的精度存在差异,且同一组数据采用不同的预测方法得到的结果也是存在很大差异。根据城市交通存在的长期相关性,对交通信息进行可预测性分析,即借助各种定性、定量分析方法判断交通系统处于确定性、混沌还是随机性变化状态[1],据此分析该交通系统未来趋势进行短期预测的可能性程度,用以预测交通系统将来的变化趋势。目前交通流分析研究主要是通过混沌理论的递归图法、Kolmogorov熵、Lyapunov指数等进行混沌辨识[2-4],从而判定交通流是否具有可预测性。然而这些方法大多需要大量的样本量,计算方法也还不够成熟,不能进行可对比度量。
由于影响交通流量的随机因素太多,非线性很强,传统的理论依据存在很大的局限性,新理论和新技术的发展一直推动着交通预测的不断发展,新方法有神经网络法[5-6]、分解模型法[7]、模糊数学法[8]、支持向量机[9]、优选组合法[10-11]、滤波理论[12]、智能优化算法[13-14]等。文献[8]使用基于区间2型模糊集理论的交通流数据长期预测方案,以较高的精度显示出交通流量变化的可能范围,但是计算过于复杂。文献[10]诱导有序加权平均(induced ordered weighted average,IOWA)算子应用到短时交通流预测中.建立了以整体预测误差平方和最小为目标的组合预测模型。文献[12]提出的卡尔曼滤波预测交通流具有模型参数少、计算相对简便的特点,但难以反映交通流量预测过程中的非线性和不确定性;文献[13]提出用遗传算法优化神经网络克服收敛速度慢、推广能力差等问题,这样就会使整个种群进化搜索效率低。不满足城市交通控制的实时性要求,限制了城市交通控制的效果,很难找到能够准确表示交通流量特征的数学模型,因此只有具体分析某个地区的交通特性才能建立起交通规理方法。
神经网络在交通流预测得到广泛的应用,以反向传播(back propagation,BP)算法应用最广,针对传统BP学习解决了隐含层权值修正问题,而对于多峰值和不可微函数不可能有效地搜索到全局极小值,该方法具有对网络参数的赋值随机性和对初始值的敏感性,导致神经网络模型在工程应用中模拟结果不稳定[15],并且不能在线学习,需要积累足够的样本后统一训练,因此不能根据新样本实时的调整网络参数。本文首先阐明交通流的可预测性能分析方法断定历史序列具有长相关性,然后建立不同时间间隔下的最优时序的变量,采用全局优化方法——思维进化算法(mind evolutionary computation, MEC)消除神经网络初始参数对学习系统复杂性的影响,避免陷入局部极小值,同时构建以神经网络为基学习器的集成学习算法,集成学习采用串行式联级的自适应增强算法(adaptive boosting,Ababoost)组合成BP_Ababoost、MEC-BP_Adaboost模型,并且通过误差平方和倒数准则重新优化Adaboost算法对弱预测器权值分布,从而在某输入状态下具有更佳的拟合效果,有效地提供单一模型的泛化能力,从而更好达到交通流的一步或多步预测。
1 交通流可预测性分析
1.1 重标极差分析法
重标极差分析法(rescaled range analysis,R/S)用来分析时间序列的分形特征和长期记忆过程[16],Hurst指数用以度量趋势的强度和噪声的水平随时间的变化指标。具有Hurst统计特性的系统,它反映的是一长串相互联系事件的结果,不依赖于通常概率统计学的独立随机事件假设,这正是分析短时交通流所需要的理论和方法。
设定一个时间序列{x(t),t=1,2,…,M},计算步骤如下。
(1)将原始时间序列分割成为长度为n的[M/n]个等长子序列段,Ia表示第a个子序列段,第a个上的时间序列段表示为{x(i),i=1,2,…,n}。Ea表示第a个子序列段上的均值,可表示为
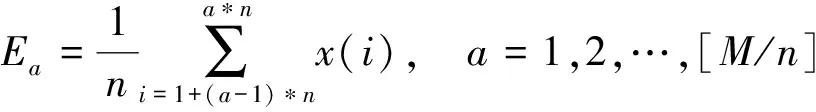
(1)
(2)子序列段Ia中元素对于均值的累积离差X(i,a)为

(2)
(3)子序列段Ia的极差(RIa)和样本标准差(SIa)可表示为
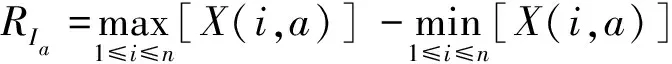
(3)

(4)
(4)子序列段长度为n划分的重标极差值(R/S)n,可表示为

(5)
1.2 基于R/S分析法的时间序列可预测分析
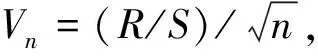
根据赫斯特指数值的不同,可以将时间序列分为3种类型。
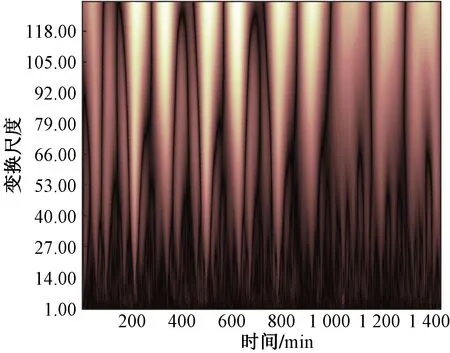
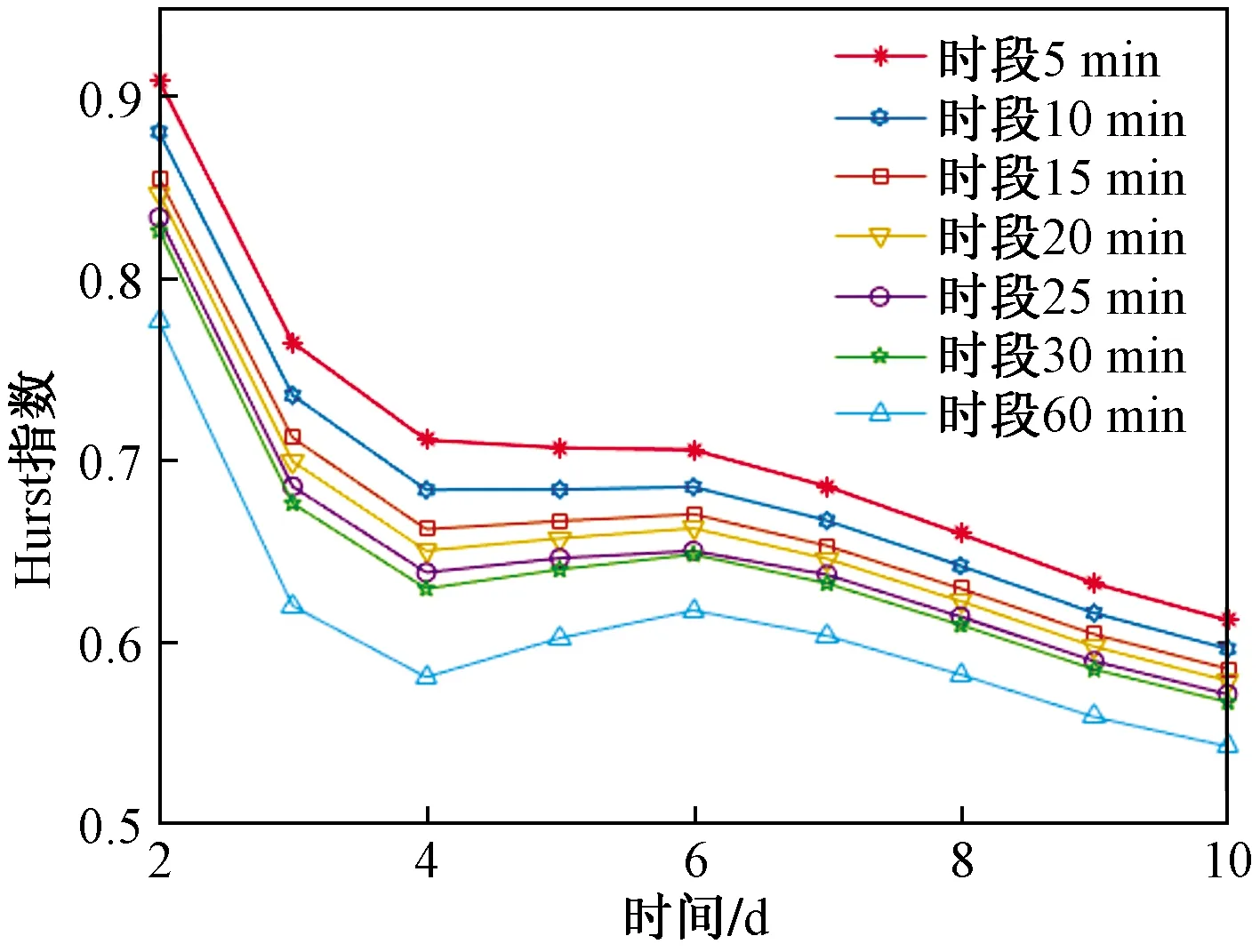
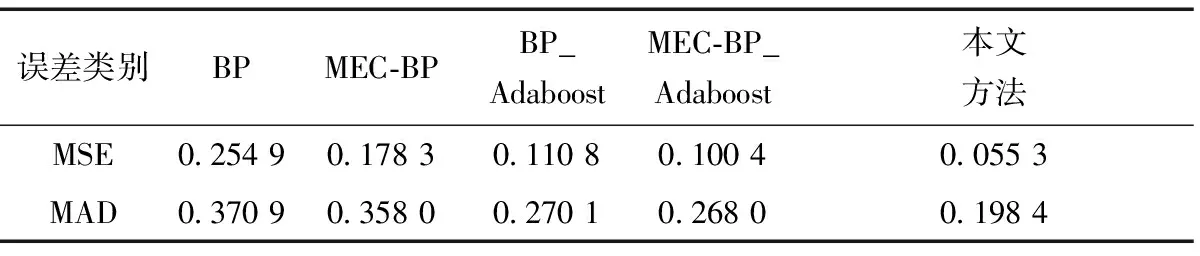
(1)0 (2)H=0.5,说明该序列是标准的随机游走序列,即未来变化趋势和过去趋势的增量没有关系。 (3)0.5 X(t)={x(t),x(t+τ),…,x[t+(m- 1)τ]}T,t=1,2,…,M (6) 式(6)中:X为m×M维矩阵,重构后所得相空间的相点个数为M=N-(m-1)τ,M个相点在m维相空间中构成一个相型,它表示交通流系统在某一瞬间的状态,按时间增长的顺序将其相连,即可描述交通流系统在m维相空间中的演化轨迹,因此将原来的一维时间序列预测问题转化成m维相点序列的预测。假设该地区交通流时间序列预测的相点{X(t),X(t-1),…,X(t-k)},k=1,2,…,t-1。已知当前时刻需要预测相点:p=1时称为一步预测;p>1时称为多步预测,预测模型可以表示为 {x[t+(m-1)τ+1],…,x[t+(m-1)τ+ p]}=F[X(t),X(t-1),…,X(t-k)] (7) 利用前馈神经网络的泛化逼近能力,实现交通流的一步或者多步预测。利用C-C方法计算嵌入维数和延迟时间,通过Wolf方法计算交通流的最大Lyapunov指数来判断交通流的混沌特性。 思维进化算法是针对遗传算法的缺陷和模仿人类思维进化过程的一种新型进化算法。其继承了遗传算法的部分思想,又引入了“趋同”和“异化”两个新的操作算子。趋同和异化分别负责局部和全局寻优,两算子一定独立且相互协调,任一操作的改进都可提高算法的整体搜索效率,且其定向学习与记忆机制,使其具有极强的全局优化能力[18]。主要利用MEC优化神经网络初始权值和阈值,其形成的MEC-BP融合算法结构如图1所示。 图1 MEC-BP融合算法结构框图Fig.1 Block diagram of MEC-BP fusion algorithm 自适应增强算法(adaptive enhancement algori-thm,Adaboost)是通过反复搜索样本特征空间,获取样本权重,并在迭代过程中不断调整训练样本的权重,增加(减小)预测精度低(高)的样本的权重,并采用加权多数表决的方法组合形成一个强预测器,即加大(减小)预测误差率较小(大)的弱预测器的权值,使得它在表决中起较大(小)作用[19],显著提高学习算法的预测性能。神经网络集成模型即把BP神经网络作为弱预测器,反复训练BP神经网络预测样本输出,通过Adaboost算法得到多个BP神经网络弱预测器组成强预测器。基于MEC优化神经网络模型集成的结构如图2所示。 算法步骤如下。 步骤1数据获取和网络初始化。从样本空间选取m组训练样本T={(Xi,yi)},赋予训练样本权重分布为w1i=1/m,i=1,2,…,m,依据样本输入和输出维数确定网络结构,神经网络初始权重和阈值由改进思维进化算法优化获得,D(1)表示获得样本的初始权重,K表示预测器的数量。 图2 基于Adaboost算法的神经网络集成结构图Fig.2 Neural network integration structure diagrambased on Adaboost algorithm D(1)=(w11,w12,…,w1 m) (8) 步骤2进行迭代。 (1)训练第k个弱预测器时,用弱预测器Hk(x)训练样本并预测训练数据输出回归误差率(ξk),计算训练集上的样本最大误差(Ek)和每个样本的相对误差(ξki),计算公式为 Ek=max[|yi-Hk(Xi)] (9) (10) (11) (2)计算该弱预测器在最终预测器中所占的权重(ak),公式为 (12) (3)根据预测序列权重ak调整下一轮训练样本的权重为 D(k+1)=(wk+1,1,wk+1,2,…,wk+1,m) (13) (14) 步骤3训练K轮后得到K组弱预测函数Hk(x),按弱预测器权重组合各个弱预测函数得到强预测器h(x)为 (15) 一般来说每种单项预测器的预测精度不同导致误差存在,为了更好地求出各组弱预测器的加权值,通过Adaboost算法训练MEC-BP神经网络得到K组弱预测器的弱预测函数Hk(x)之后,再次采用预测误差平方和倒数准则进行每组弱预测函数的加权值求解,最终得到累加的强预测器h(x)=∑wkHk(xk,ak)。预测误差平方和越大,表明该项预测模型的预测精度就越低,从而它在组合预测中重要性就降低,对预测误差平方和较小的单项预测模型在组合预测中的应赋予较大加权系数。加权系数计算方法为 (16) 设yki为第k种弱预测器在第i时刻的预测值,yi为同一预测对象的第i时刻观测值,eki为第k种预测器在第i时刻的预测值和观测值的偏差,则Ek为第k种弱预测器的预测误差平方和。 (17) 选取美国PeMS(portable emission measurement system)系统上的交通流数据进行交通流预测模型分析与预测。PeMS系统中的源数据有两种:30 s的交通流量和车道占有率,它将30 s数据聚合生成5、15、60 min等数据集。①实验数据集1:采集时间2011年5月2日—2011年5月5日连续4 个工作日的单个路段车流聚合,采用5 min统计尺度下记录交通流数据;②实验数据集2:采样时间为2011年6月1日—2011年6月5日(周三~周日)连续 5个日期的3 个路段车流聚合,观测时间为每天连续24 h,采用5、10、15、20 min不同统计尺度下记录交通流数据,分别得到了1 440、720、480、360 个数据。数据集2交通流数据曲线如图3所示。 图3中曲线之间的相似性说明在不同尺度上,交通流变化存在自相似性,观察时段5 min数据中交通流时间序列的变化趋势,可以发现交通流数据呈现出明显的准周期性趋势。为识别交通流数据的自相似性,采用小波变换对交通流数据进行分解,如图4所示交通流数据的小波分解系数,小波系数指相似性指数(RI),RI越大自相似越大,由于出行需求的变化,工作日(前3 d)和周末(后2 d)的小波系数有所不同,说明交通流具有时段性,故可将交通流数据时段分为高峰时段、空闲时段和正常时段。实验数据表明,交通流时间段可以分为:忙碌时段为07:30—09:30,14:30—18:30;空闲时段为00:00—05:00;其余为正常时段。 图3 连续5 d不同统计尺度交通流时间序列Fig.3 Time series of traffic flow at different statistical scales for 5 consecutive days 图4 5 min间隔的短期交通流小波变换实部时频分布Fig.4 Real-time time-frequency distribution of short-time traffic flow wavelet transform at 5 min intervals R/S分析法求解Hurst值会受到样本量的影响,为了对不同观测尺度的数据进行进一步的跟踪对比,以交通流的自然周期1 d为单位对交通流序列进行累加,最大限度地保留周期内表征交通流序列的变化规律的信息计算,对数据集2交通流的分析如下。 (1)图5为不同统计尺度不同天数的Hurst变化曲线,表明Hurst指数的值均位于区间[0.5, 1],表示交通流时间序列具有长期的记忆性质,表明交通流变化的整体方向将继承过去的整体趋势,过去的增加(减少)趋势预示未来的增加(减少)趋势。图5中每条曲线都随着时间长度的增加而呈整体下降趋势, 即Hurst指数随样本量的增加而降低,这表明在同一统计尺度范围内,当时间序列达到一定的尺度后,再增加数据,将破环原时间序列的自相似性;相同时间长度下Hurst指数随时间统计尺度(σ)的增加而呈现下降趋势,交通流序列具有短时有效性,随着时间的增长,时间序列的长记忆性减弱。 (2)表1为3种不同时段对不同统计尺度相同天数(5 d)的Hurst指数的计算,结果表明,相同统计尺度交通流从空闲时段到忙碌时段的Hurst指数呈递增趋势,这是因为对相同时间尺度下,交通越忙自相似越强,交通的可预测性越强;同一时段不同尺度的Hurst指数呈递减趋势,预计随着统计尺度的不断增大,Hurst指数越接近0.5,交通流没有分形特征,主要是因为过去与未来不同存在了相关性时间序列为完全独立过程。 (3)如果时间序列是具有长程相关性的,时间之间的相互依赖性是很强的。图6给出了在统计尺度10 min的交通流时间序列的lg(R/S)n和Vn关于lgn变化曲线,可看出原始序列出差持续上升并达到n=207时达到最大,然后急剧下降,所以可以断定统计尺度10 min的交通流的平均循环周期为 207 min,也就是说该序列平均经过207 min就失去了对初始条件的记忆;同时发现打乱序列后的Hurst指数(0.623 3)小于与原始序列的Hurst指数(0.703 1),这是由于数据经打乱之后,破坏了原始序列的相关性结构,交通流时间序列的有序程度降低;打乱序列后发现是一条平坦的曲线,说明该序列变成独立随机过程不具备长程相关性。 表1 不同时段不同统计尺度相同天数的Hurst指数 图5 不同统计尺度的Hurst指数曲线Fig.5 Hurst exponent graphs of different statistical scales 图6 lg(R/S)n和Vn关于lgn变化曲线Fig.6 The change curve of lg(R/S)n and Vn about lgn (4)图7为相同时间长度不同统计尺度下得到的Vn随lgn的变化曲线,发现随着统计尺度的减小则 所突变时间越长,即长记忆消失所需要的时间越长,但实际上这种长期的记忆性并非无穷长的,而是随时间逐渐减弱直至忘却,所以短时预测仍有可能。当τ为60 min时该Vn统计量曲线上升趋势不明显,Hurst指数越接近0.5,则序列中的噪声越多,序列越接近随机过程。 (5)为了定量描述交通流的复杂性,对基于分形、混沌和熵的交通复杂性进行分析,如表2所示,Hurst指数和样本熵随着统计尺度的增加而逐渐减小,发现5 min采样的样本熵最大,则时间序列就越复杂;最大Lyapunov指数始终为正数,则该系统必定在某一矢量方向上的运动是不稳定的,同时意味着这一方向上有混沌吸引子的出现,是整个系统的运动处于混沌状态。 图7 相同时间长度不同统计尺度下得到的Vn随lgn的变化曲线Fig.7 Variation curve of Vn with logn obtained under different statistical scales of the same time length (18) (19) 式中:n为交通流数据序列的长度;yt表示t时刻的预测值;dt表示t时刻的实际值;均方误差(MSE)和平均绝对误差(MAD)的指标越小,表明相应模型的结构越合理。 在MATLAB仿真软件对传统BP、BP_Adaboost、MEC-BP方法和MEC-BP_Adaboost模型和改进MEC-BP_Adaboost模型(本文方法)进行训练,并利用训练好的模型对数据集1进行短时交通流单步预测,结果如表3、图8和图9。 表2 不同统计尺度下交通流特征复杂性分析 从表3、图8、图9可知,基于MEC-BP模型与传统BP模型相比,均方误差和平均绝对误差分别下降29.8%和3.5%,证明MEC在优化BP模型的初始参数方面的有效性;基于BP_Adaboost模型和传统BP模型相比,均方误差和平均绝对误差分别下降56.3%和27.1%,证明Adaboost算法对神经网络的泛化能力有极大的提升,表明Adaboost 算法采用加权多数表决的方法,能有效提高模型的预测精度及避免模型“过拟合”现象的发生;基于本文方法与BP模型相比,均方误差和平均绝对误差分别下降78.2%和46.4%,证明本文方法对交通流预测具有合理性;基于本文模型和MEC-BP_Adaboost模型相比,均方误差和平均绝对误差分别下降44.9%和25.9%,证明了采用误差平方和倒数准则对弱预测器的权值大小,使弱预测器预测精度更高,更有效地提高预测器的泛化能力。 表3 不同预测模型性能指标比较 图8 不同模型下的短时交通流的预测值比较Fig.8 Comparison of predictions of short-term traffic flow under different models 为了更好地表现出每个弱预测器的预测效果,通过预测误差平方和倒数方法进行每组弱预测函数的权值求解,使每个弱预测器的性能更好地表现出来,提高整个模型的决策性能,本文方法和MEC-BP_Adaboost模型的每个弱预测器权重比较如表4所示。同时针对时间段交通状态,R/S分析了每天不同时段的交通流存在相关性,但是不同时段可能有不定性因素存在,则交通流预测可能存在差异,如表5所示。 由表4实验结果可以看出,根据10个MEC优化神经网络的改进后的权值大小对比发现,MEC-BP_Adaboost模型的第3、4、8的神经网络权值占比最大,说明这3 个神经网络对交通流预测效果更明显,通过本文方法的改进之后,降低其他神经网络对模型的影响小的权重,加大了这3 个神经网络对整体模型影响的比重,充分利用该网络提供的有价值的信息,将预测结果的精确度最大化,这是因为各弱预测器的权重得到不断优化,Adaboost算法的提升能力得到不断增强,该模型有效的克服了时间序列突变带来的预误差,有较好的拟合真实的交通误差。由表5展现出不同时段状态下采用本文方法比之前的方法预测误差更小,达到更精准预测效果,证明本文方法的有效性。 为进一步验证模型的有效性和普适性,采用数据集2进行2、3、4、5 步预测,如表6所示,因此随着预测步数的增加,本文方法的预测误差普遍小于原方法,但随着相同模型下,随着步长的增加预测精度下降,因此交通流存在短期的预测能力。 图9 不同模型的预测值与估计值误差绝对值比较Fig.9 Comparison of the absolute value of the error between the predicted value and the estimated value of different models 表4 两种模型中每个弱预测器的权重对比 表5 不同时间段预测的MSE值对比 表6 不同模型不同预测步长的MSE值对比 针对短时交通流量的不确定性、复杂性和高度非线性的基本特征,R/S分析法应用于短时交通流分析,能揭示微观交通流运动的内在规律,抑制随机因素的影响,定量地揭示交通系统的动态学特性。该文采用思维进化算法优化BP神经网络的初始参数选取,提高神经网络的预测精度,将多个思维进化算法优化后的网络进行集成有效综合决策,提高网络的泛化性,该模型是研究非线性时间序列预测的一种尝试,通过对交通流实例的短期预测,从而证实该模型具有实用性,可为类似的具有周期特性的时间序列提供一种新的预测方法。 在预测过程中仅对该城市交通流时间特性进行分析研究,并未对其他影响因素进行考虑分析,如天气状况、突发事件等,这将导致预测模型依赖原始数据,而原始数据的可靠性将直接影响预测结果的准确度,即使是在同一地点不同时刻段内的交通流也不可相互替换。根据表6可知,本文方法对数据量大的样本预测效果不明显,存在一定的局限性,利用过去的学习经验加速对于新任务的学习,机器学习各分支都已展开了对迁移学习的研究。在后续研究中需对其他影响因素做进一步量化分析,将其运用于交通流预测中,综合考虑以平衡对数据的过依赖性。2 基于神经网络的短时交通流实时建模预测
2.1 交通流时间序列相空间重构
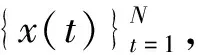
2.2 MEC-BP融合算法

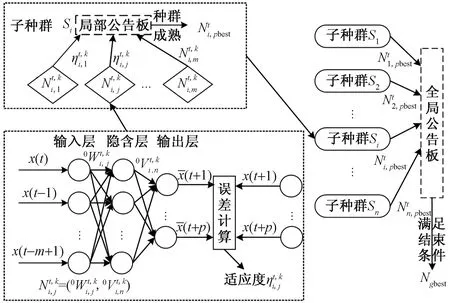
2.3 基于Adaboost算法的神经网络集成预测模型
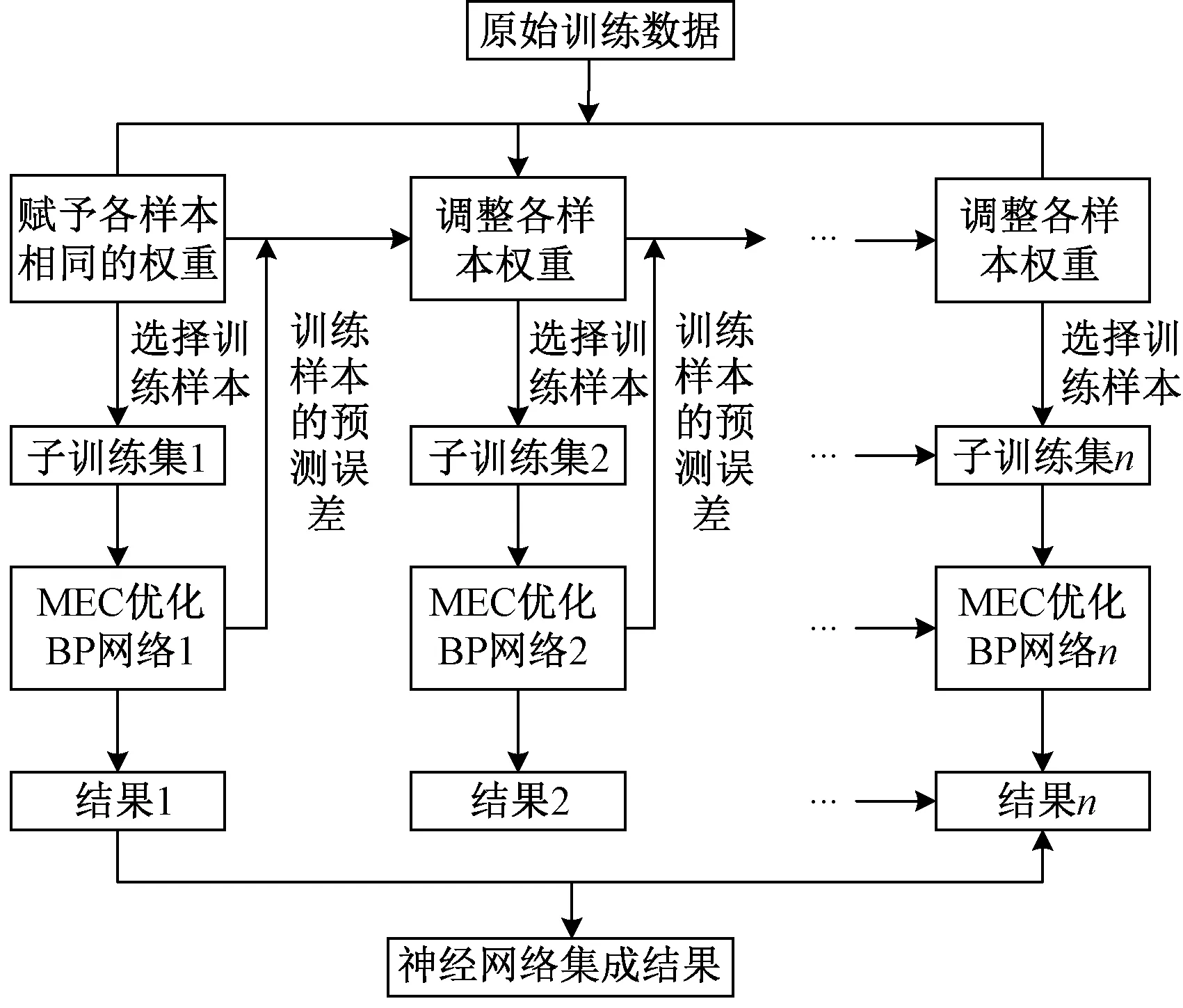





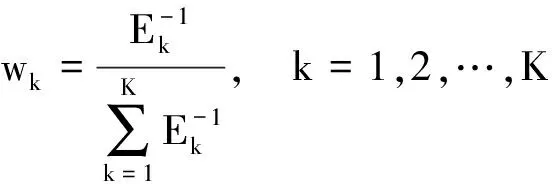

3 实验验证
3.1 数据来源与分析

3.2 基于分析法对短时交通流可预测分析结果


3.3 模型预测分析



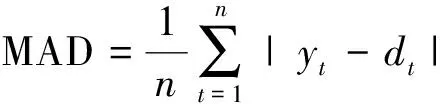


4 结论