轮式拖拉机转向特性仿真分析
韩 冰, 徐立友
(河南科技大学车辆与交通工程学院, 洛阳 471003)
拖拉机的转向性能是机动性能的重要组成部分,转向性能的优劣直接影响着拖拉机的操纵稳定性、安全性能、作业效率等整机性能[1]。近年来,中外学者对转向特性在汽车方面的研究比较多,而对拖拉机方面的研究较少。文献[2]对转向梯形结构参数进行优化设计,使优化后的拖拉机转向特性曲线接近理想转向特性曲线,减少轮胎磨损;文献[3]将汽车的稳态转向特性分为不足转向、中性转向和过多转向,并基于转向半径公式,对汽车的稳态转向特性进行分析;文献[4]为获得变速转向工况下的动力特性,建立二自由度数学模型,对汽车匀变速输入条件下的操纵稳定性进行了仿真分析。
现以某轮式拖拉机为工程实例,建立满足稳态转向特性的三自由度动力学模型及转向轨迹数学模型,分析变结构参数对轮式拖拉机稳态转向特性的影响。研究轮式拖拉机的转向性能有助于设计更加合理的转向系统,同时可为整车的结构设计及强度计算等提供理论支持。
1 拖拉机转向运动学分析
轮式车辆转向的运动学条件是转向过程中各车轮均与地面做纯滚动。为满足这一点要求,车辆在转向时各轴心线应通过同一瞬心轴线[5],即所有车轮的轴线相交于一点,如图1所示的O点。当转向盘转到极限位置,外转向轮偏转到最大值时,外侧转向轮的中心到外转向轮与地面接触点的距离为最小转弯半径,其转角及其半径关系[6]为
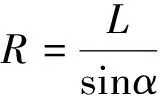
(1)
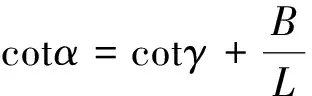
(2)
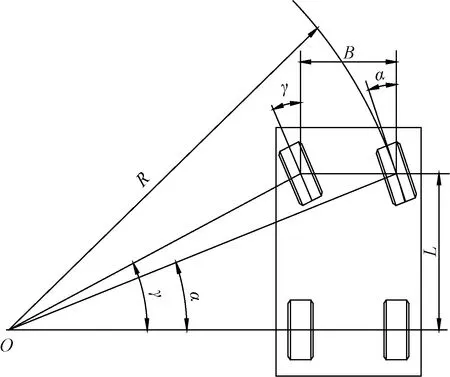
α为转向外侧前轮转角,rad;γ为转向内侧前轮转角,rad;R为最小转弯半径,m;B为轮距,m;L为前后轮间的轴距,m图1 拖拉机转向运动学模型Fig.1 Kinematic model of tractor steering
2 拖拉机3自由度动力学模型
拖拉机在行驶过程中,横摆运动与侧倾运动相互影响,故3自由度模型更符合拖拉机的实际摆动情况。根据经典力学理论及轮胎受力建立3自由度拖拉机转向动力学模型[7],如图2所示。
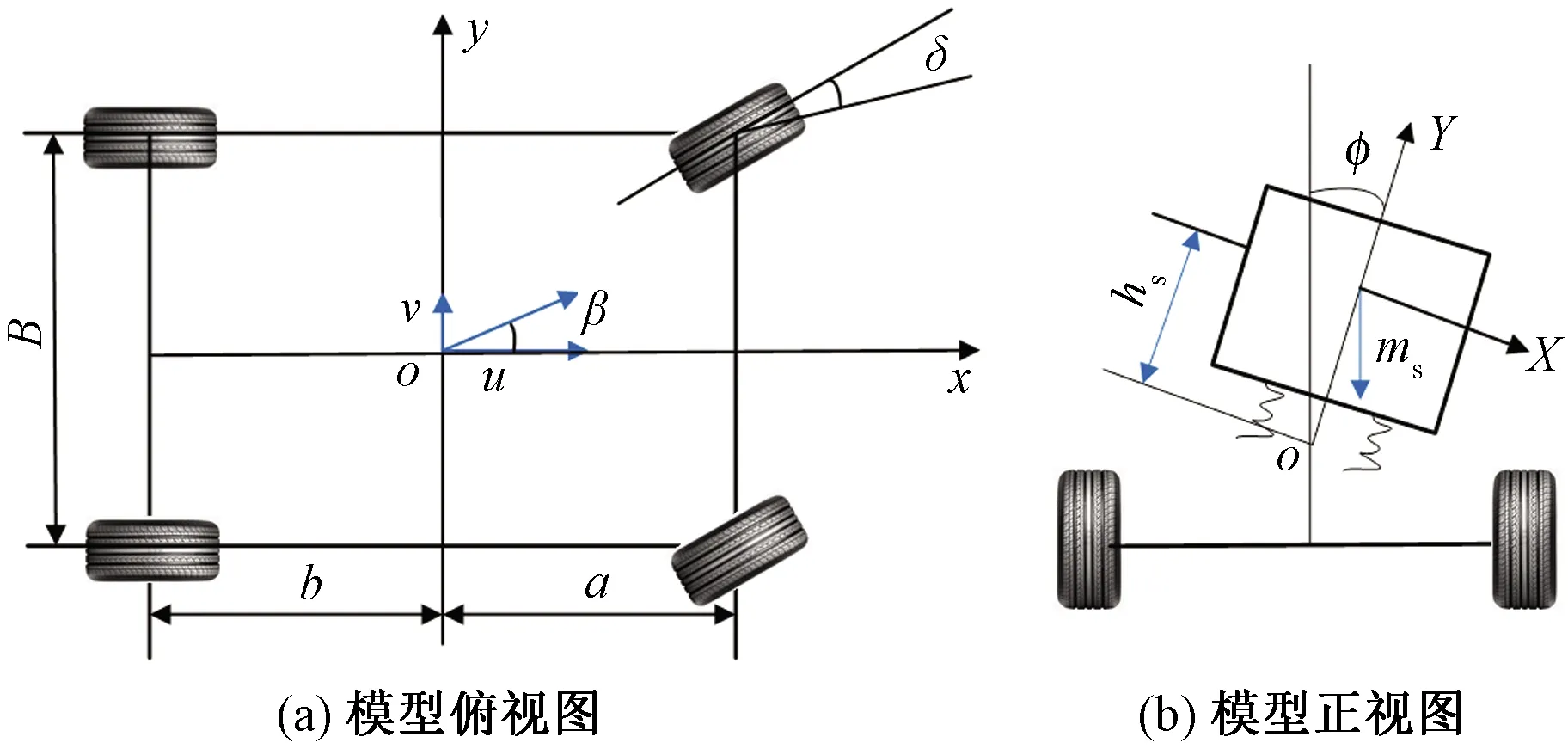
δ为前轮转角,rad;a、b分别为前轴、后轴到质心的距离,m;u为沿x轴方向的前进速度,m/s;v为沿y轴方向的前进速度,m/s;β为质心侧偏角,rad;φ为侧倾角,rad;hs为侧倾中心到质心的距离,m;ms为悬挂质量,kg图2 3自由度转向动力学模型Fig.2 Dynamic model of three degree of freedom steering
建立运动微分方程[8]为
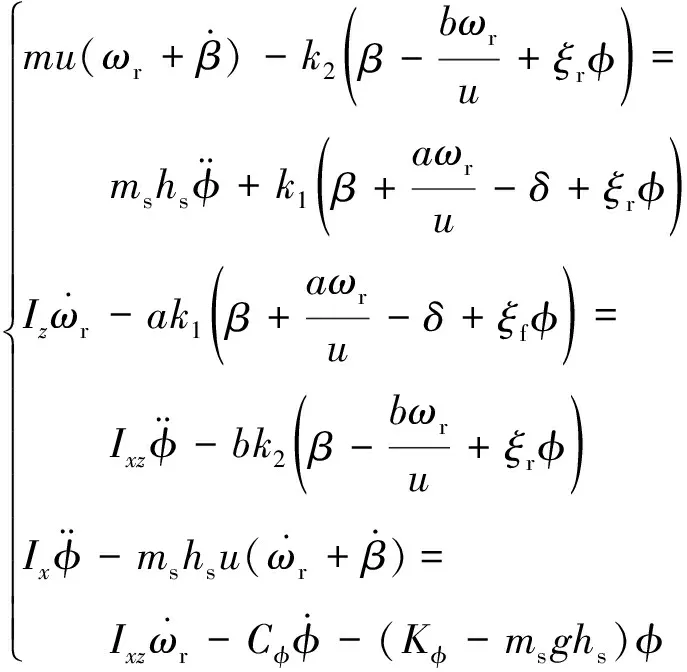
(3)
式(3)中:m为总质量,kg;ωr为横摆角速度,rad/s;k1、k2为分别前轮、后轮侧偏刚度;Ix为绕x轴的转动惯量,kg·m2;Iz为绕z轴的转动惯量,kg·m2;Ixz为绕x轴和z轴的惯性矩,kg·m2;Cφ为侧倾阻尼,N·m/(rad·s-1);Kφ为侧倾刚度,N/rad;ξf、ξr分别为前轮、后轮侧倾转向系数。
3 拖拉机转向轨迹模型
采用坐标随时间变化的函数关系来对拖拉机的行驶轨迹进行研究,以拖拉机车轮的速度和转角为输入因子,通过建立拖拉机前轮转向轨迹运动模型,找到拖拉机质心随时间的坐标变化方程[9-10],并利用MATLAB软件画出拖拉机的运行轨迹图。
如图3所示,拖拉机以前后桥中心的连线为轴,以质心p为原点建立平面坐标系。
选取质心p为研究对象,假设拖拉机经历了tk到tk+1时间的转向后,其位置变化如图4所示。
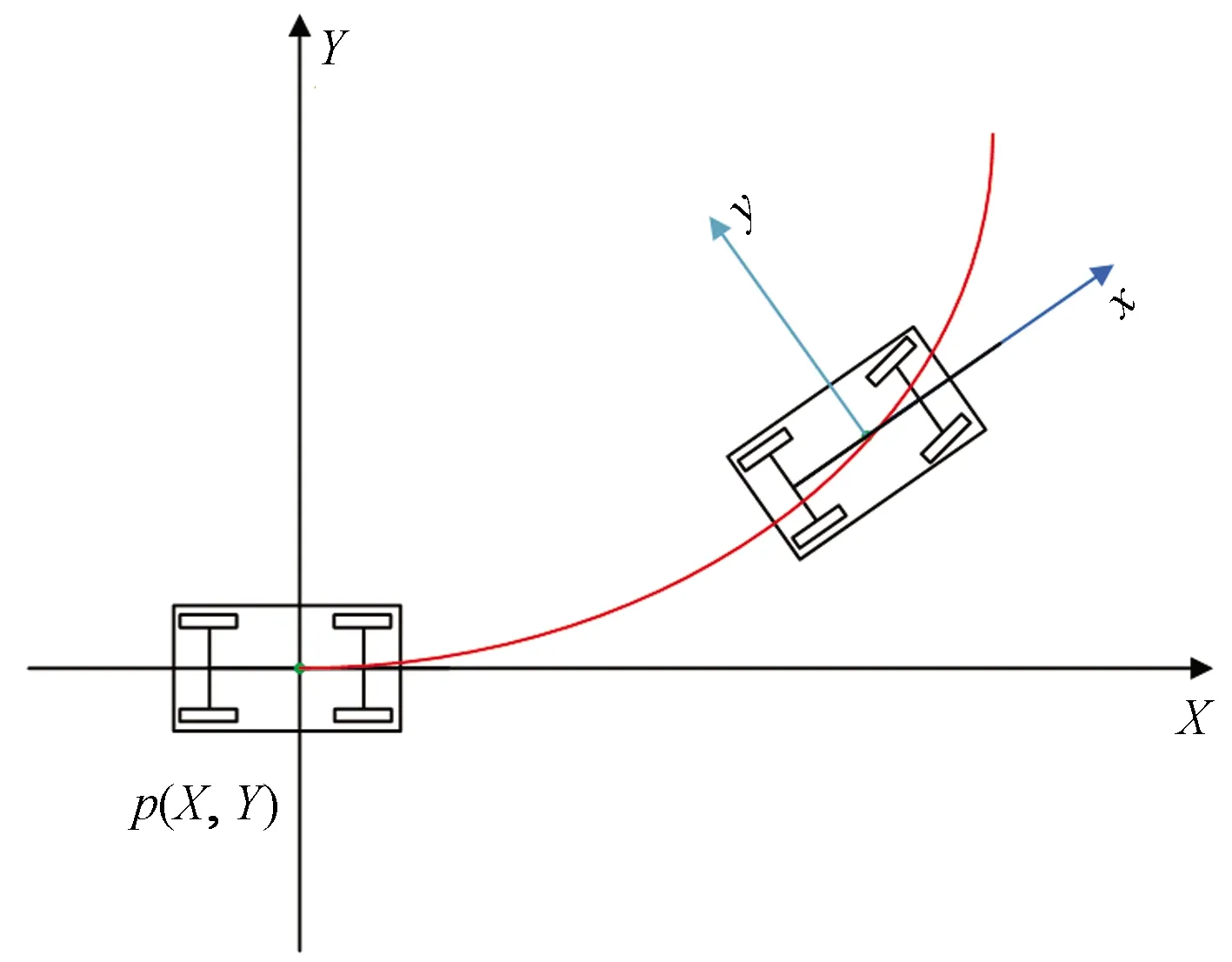
p(X,Y)为拖拉机质心的位置;红色弧线为质心p的轨迹图3 拖拉机前轮转向坐标系Fig.3 Tractor front wheel steering coordinate system

O为拖拉机的转向中心;pk、pk+1为质心运动的两个连续位置,xp、xp+1为拖拉机质点的速度方向;yp、yp+1为拖拉机质点垂直于速度的方向;dX、dY为tk到tk+1时间内拖拉机沿x轴和y轴行驶的距离;Ψp为拖拉机的航向角,rad;θp为拖拉机的横摆角,rad;αp为拖拉机xp、xp+1速度方向的夹角,rad图4 拖拉机前轮转向轨迹运动模型Fig.4 The model of tractor front wheel steering track
当tk到tk+1时间差足够小的情况下,由图4中的几何关系可以得到
dz=Rωdt
(4)
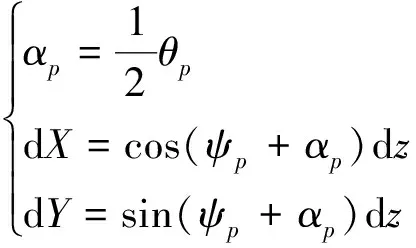
(5)
式中:z为拖拉机行驶距离,m。
将式(1)、式(4)代入,并对式(5)积分,即可得质心p在t时间内所经过的每个点的横纵坐标,这些点的连线即为质心p在t时间内的运行轨迹,p点的初始坐标为(0,0),则
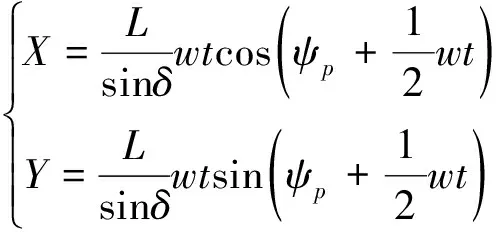
(6)
4 拖拉机转向特性仿真分析
4.1 拖拉机整车参数
在建立3自由度动力学模型和转向轨迹模型的基础上,在MATLAB中建立前轮转角输入信号时间序列,以角阶跃输入为前轮转角输入,对拖拉机转向系统进行仿真试验。仿真采用的某拖拉机模型参数如表1所示。
仿真中假设拖拉机行驶速度和转向系统传动比都恒定,当拖拉机以恒定速度直线行驶时,驾驶员突然给转向盘一个很小的角阶跃输入,即
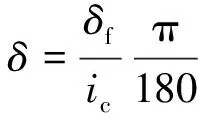
(7)
式(7)中:δf为方向盘的输入转角;ic为转向系传动比。
4.2 拖拉机速度变化对转向的影响
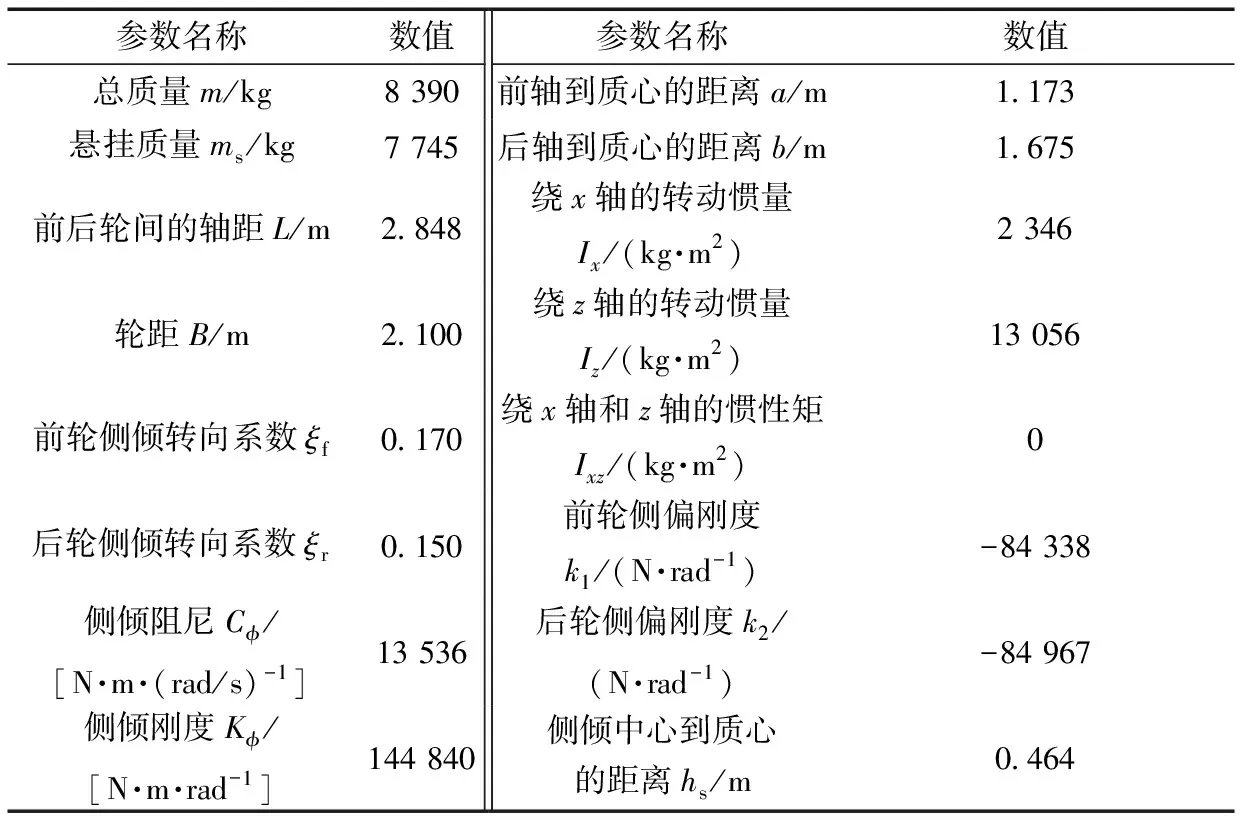
表1 拖拉机模型参数
为了分析拖拉机速度对转向特性的影响,分别对拖拉机运动进行横摆角速度仿真、侧倾角仿真和转向轨迹仿真。
在仿真时,设拖拉机在低速2.5 m/s 和高速 5 m/s 进行角阶跃仿真分析,将仿真时间取为6 s,得到横摆角速度和侧倾角响应曲线,如图5(a)和图5(b)所示;在其他条件不变的情况下,将仿真时间取为10 s,得到拖拉机在低速和高速条件下的转向轨迹曲线,如图5(c)所示。
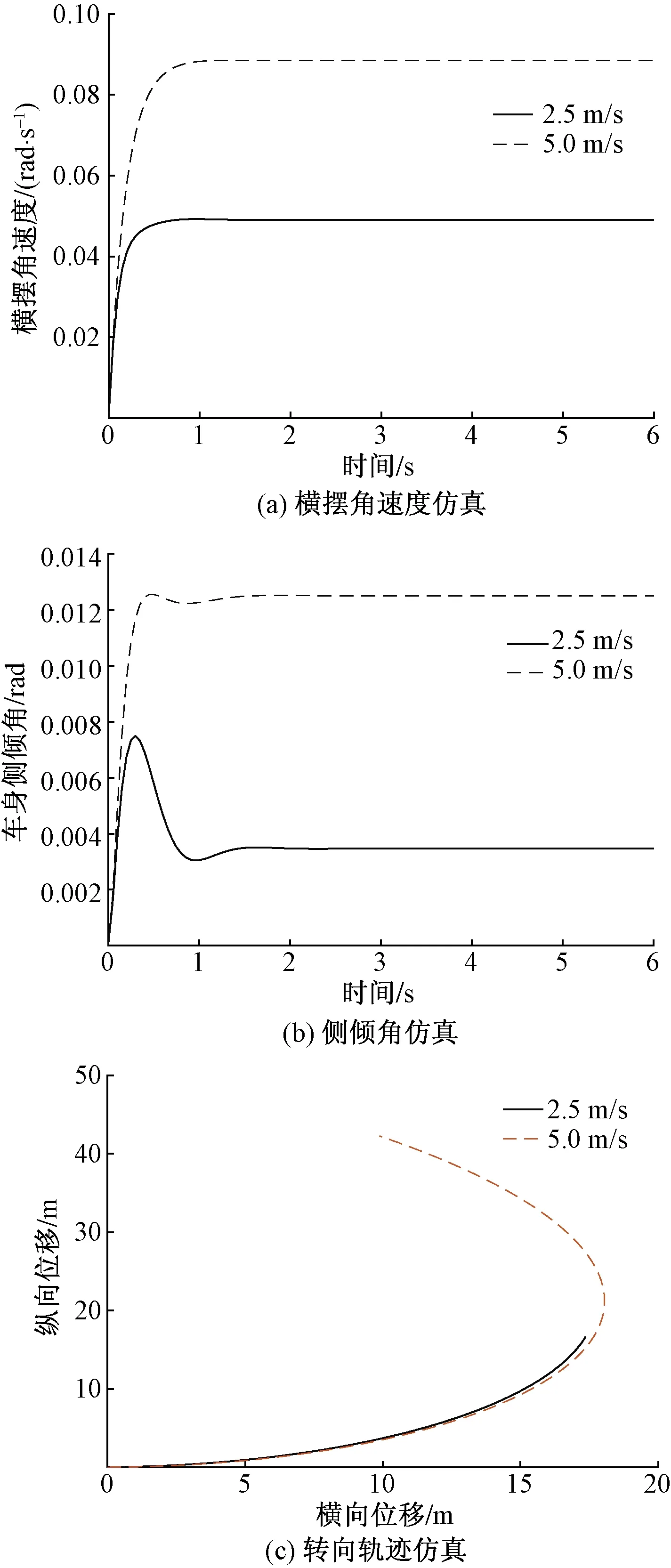
图5 速度变化下的转向特性仿真Fig.5 Simulation of steering characteristics under speed change
由图5(a)可知,当拖拉机行驶速度为5 m/s时,横摆角速度的稳态值和超调量更大,且拖拉机达到稳态所需的时间延长,故拖拉机低速行驶时转弯更加平稳;由图5(b)可知,拖拉机转弯时行驶速度越大,则稳态时的侧倾角越大,超调量越小,达到稳态时的反应时间缩短,故拖拉机高速行驶时转弯稳定性变差;由图5(c)可知,拖拉机以低速行驶时的转弯半径相对较小,而高速行驶时其转弯半径相对较大,且转过距离相对较长,增加了驾驶难度。
4.3 拖拉机质心到前轴距离变化对转向的影响
为分析质心到前轴距离变化对转向的影响,设定质心到前轴的距离分别为0.973、1.173、1.373 m,拖拉机行驶速度为2.5 m/s。仿真结果如图6所示。
由图6(a)可知,质心到前轴的距离增加,则拖拉机横摆角速度的稳态值和超调量增加,达到稳态时的反应时间延长;由图6(b)可知,随着质心到前轴的距离增大,拖拉机的稳态侧倾角加大,超调量减小,故拖拉机行驶时稳定性变差;由图6(c)可知,随质心到前轴距离减小,转弯半径变小,可以转过半径较小的弯道。
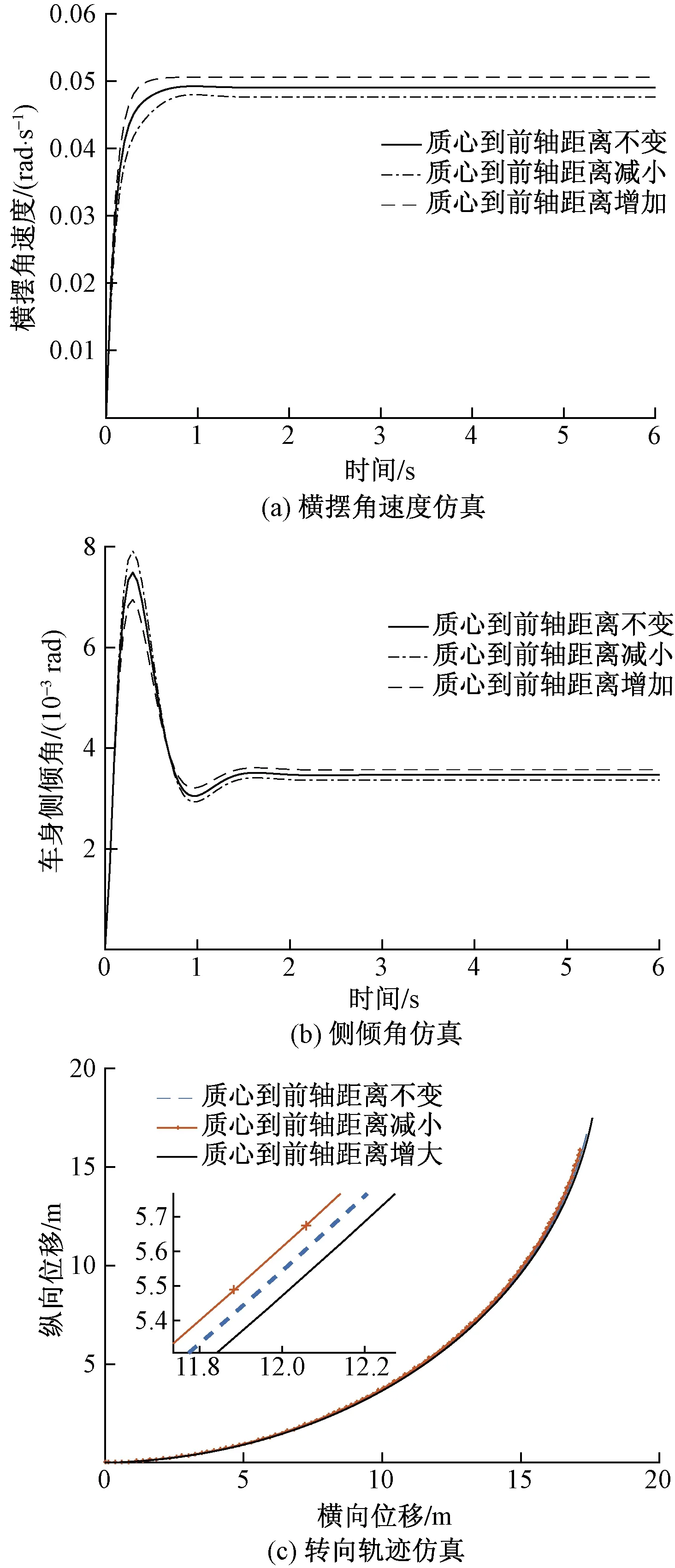
图6 质心到前轴距离变化下的转向特性仿真Fig.6 Simulation of steering characteristics with the change of distance from center of mass to front axle
4.4 拖拉机簧载质量变化对转向特性的影响
为分析簧载质量对转向的影响,设定簧载质量分别为7 890、8 390、8 890 kg,拖拉机行驶速度为2.5 m/s仿真结果如图7所示。
由图7(a)可知,随簧载质量减小,拖拉机横摆角速度的稳态值和超调量增加,达到稳态时的反应时间延长;由图7(b)可知,随着簧载质量增大,拖拉机的稳态侧倾角加大,超调量减小,达到稳态时的反应时间缩短,稳定性变差;由图7(c)可知,随簧载质量的减少,转弯半径变小,簧载质量增大,其转过的距离相对较长。
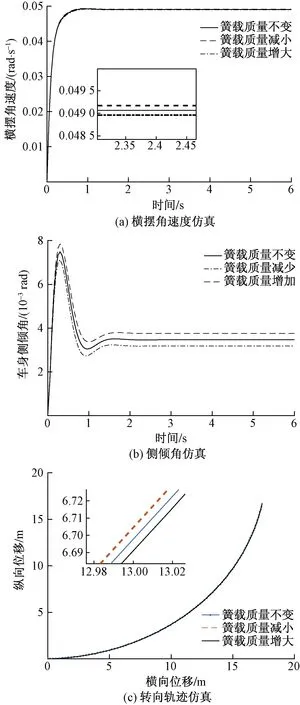
图7 簧载质量变化下的转向特性仿真Fig.7 Simulation of steering characteristics under the change of sprung mass
4.5 拖拉机侧倾中心到质心的距离变化对转向的影响
为分析侧倾中心到质心的距离变化对转向的影响,设定侧倾中心到质心的距离分别为0.364、0.464、0.564 m,拖拉机行驶速度为2.5 m/s。仿真结果如图8所示。
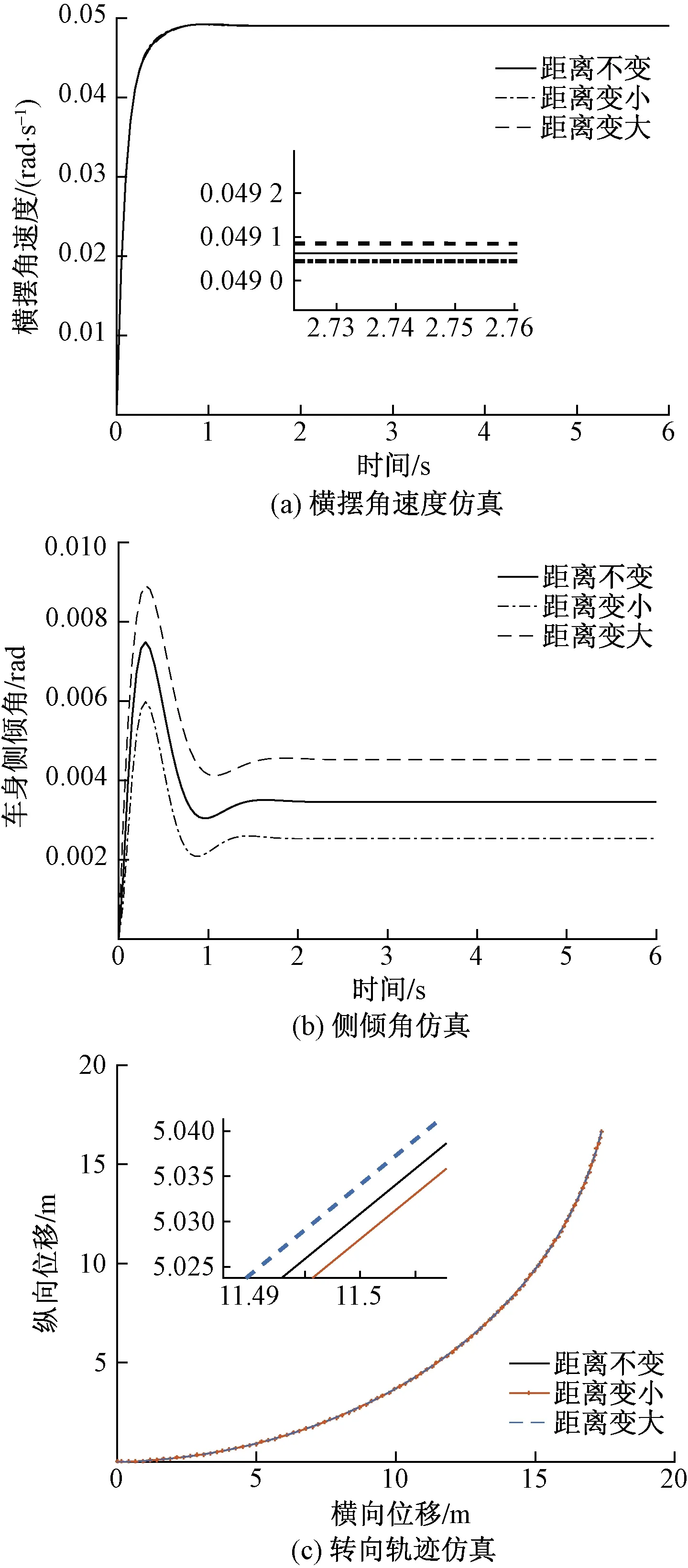
图8 侧倾中心到质心距离变化下的转向特性仿真Fig.8 Simulation of steering characteristics with changing distance from roll center to mass center
如图8(a)所示,对比侧倾中心到质心的距离的横摆角速度曲线,随侧倾中心到质心的距离增加,拖拉机横摆角速度的稳态值和超调量增加,达到稳态时的反应时间延长,侧倾中心到质心的距离减小的结果与之相反;由图8(b)可知,随着侧倾中心到质心的距离增大,拖拉机的稳态侧倾角加大,超调量减小,达到稳态时的反应时间缩短,稳定性变差,由图8(c)可知,在同样的转向盘转角输入下,随侧倾中心到质心的距离变大,转弯半径变小,可以转过半径较小的弯道,侧倾中心到质心的距离减小,其转过的距离相对较长。
4.6 拖拉机轮胎侧偏刚度变化对转向特性的影响
为分析轮胎侧偏刚度变化对转向的影响,在拖拉机行驶速度为2.5 m/s时,分别对拖拉机运动进行角阶跃响应仿真和转向轨迹仿真。设定前轮侧偏刚度分别为-84 338、-74 338、-94 338 N/rad,后轮侧偏刚度分别为-74 967、-84 967、-94 967 N/rad,得到横摆角速度、侧倾角响应曲线和转向轨迹曲线,如图9所示。
由图9(a)可知,随前轮和后轮的侧偏刚度增加,拖拉机横摆角速度的稳态值和超调量增加,达到稳态时的反应时间延长,前轮和后轮的侧偏刚度减小的结果与之相反;如图9(b)所示,对比轮胎侧偏刚度的侧倾角曲线,随着轮胎侧偏刚度增大,拖拉机的稳态侧倾角加大,超调量减小,达到稳态时的反应时间缩短,稳定性变差;由图9(c)可知,在同样的转向盘转角输入下,随轮胎侧偏刚度增加,转弯半径变小,可以转过半径较小的弯道。
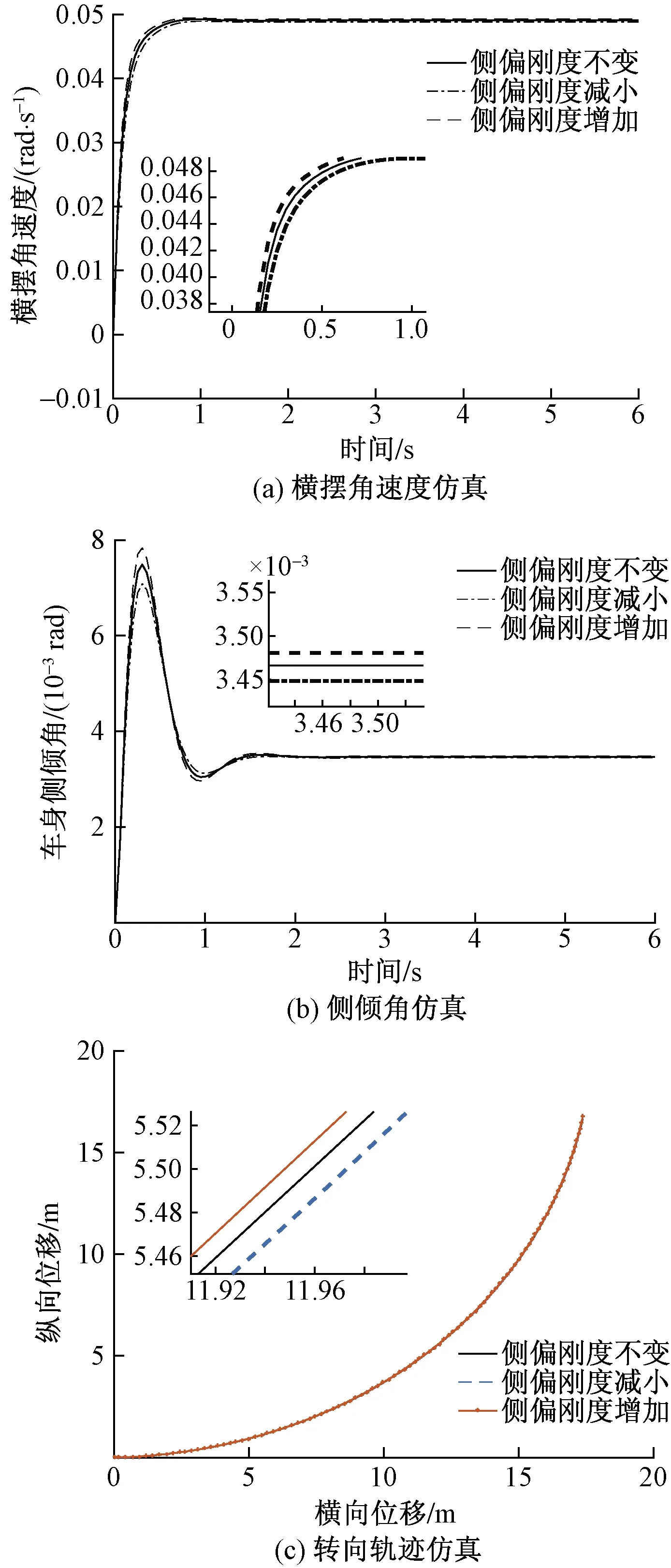
图9 轮胎侧偏刚度变化下的转向特性仿真Fig.9 Simulation of steering characteristics under tire cornering stiffness variation
4.7 拖拉机侧倾刚度变化对转向特性的影响
为分析侧倾刚度变化对转向的影响,分别对拖拉机运动进行角阶跃响应仿真和转向轨迹仿真。设定侧倾刚度分别为134 840、144 840、154 840 N·m/rad,拖拉机行驶速度为2.5 m/s。仿真结果如图10所示。
如图10(a)所示,对比侧倾刚度变化下的横摆角速度曲线,侧倾刚度减小,则拖拉机横摆角速度的稳态值和超调量增加,达到稳态时的反应时间延长;由图10(b)可知,随着侧倾刚度增大,拖拉机的稳态侧倾角加大,超调量减小,达到稳态时的反应时间缩短;由图10(c)可知,在同样的转向盘转角输入下,随侧倾刚度减小,转弯半径变小,侧倾刚度增加,其转过的距离相对较长。
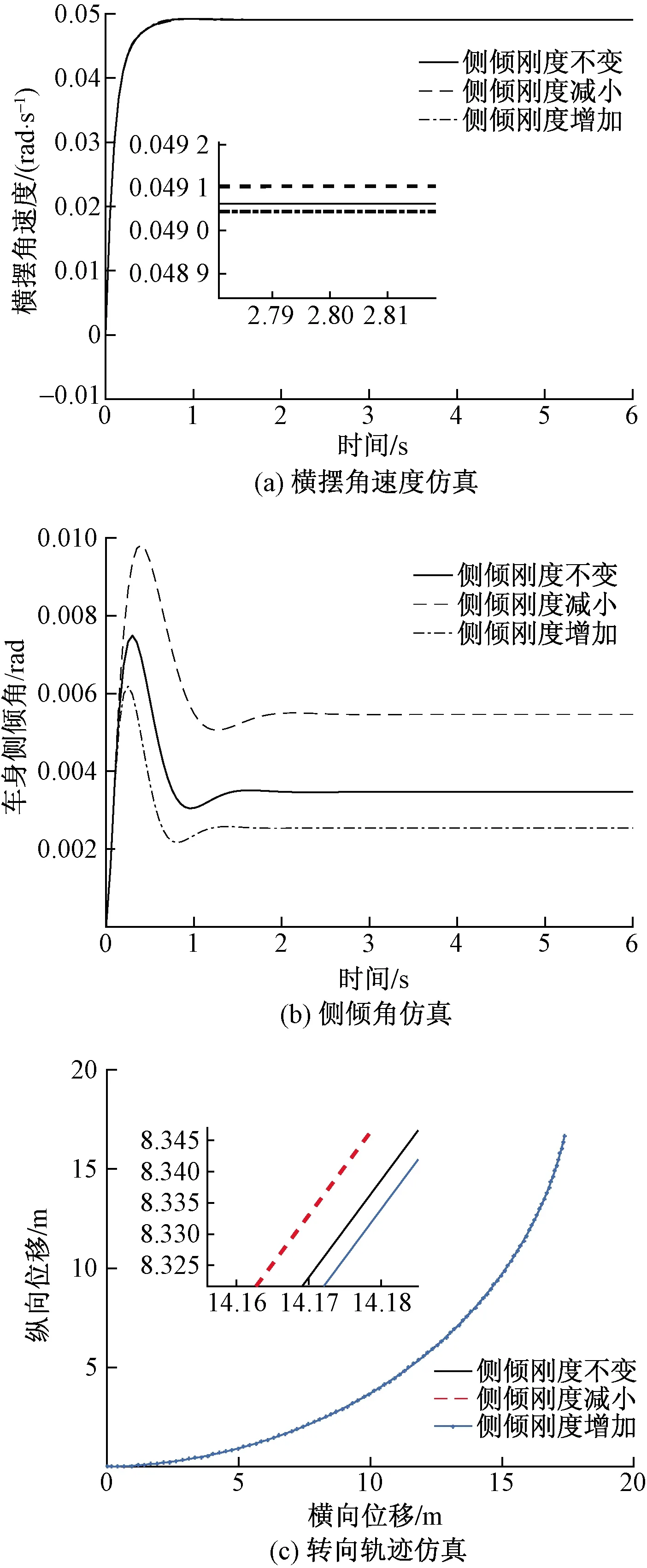
图10 侧倾刚度变化下的转向特性仿真Fig.10 Simulation of steering characteristics with roll stiffness variation
4.8 拖拉机结构参数变化对转向特性的影响
综上,仿真表明当转向盘转角输入一定时,随速度、质心到前轴的距离、侧倾中心到质心的距离及侧偏刚度的增大,簧载质量和侧倾刚度的减小,横摆角速度的稳态值增加,反应时间延长,不稳定状态到稳定状态的回复能力变弱;随速度、质心到前轴的距离、簧载质量、侧倾中心到质心的距离、侧偏刚度和侧倾刚度的增大,侧倾角稳态值增加,拖拉机转弯行驶时的稳定性变差;随速度、质心到前轴的距离、簧载质量及侧倾刚度的增大,侧倾中心到质心的距离和侧偏刚度的减小,转向半径增大,转弯行驶时的灵活性变差。
由表2可知,拖拉机行驶速度为2.5 m/s时,质心到前轴的距离、侧偏刚度及侧倾刚度对稳态横摆角速度的影响较大;簧载质量、侧倾中心到质心的距离及侧倾刚度对稳态侧倾角的有影响较大;质心到前轴的距离、侧偏刚度及簧载质量对转弯半径的影响较大。
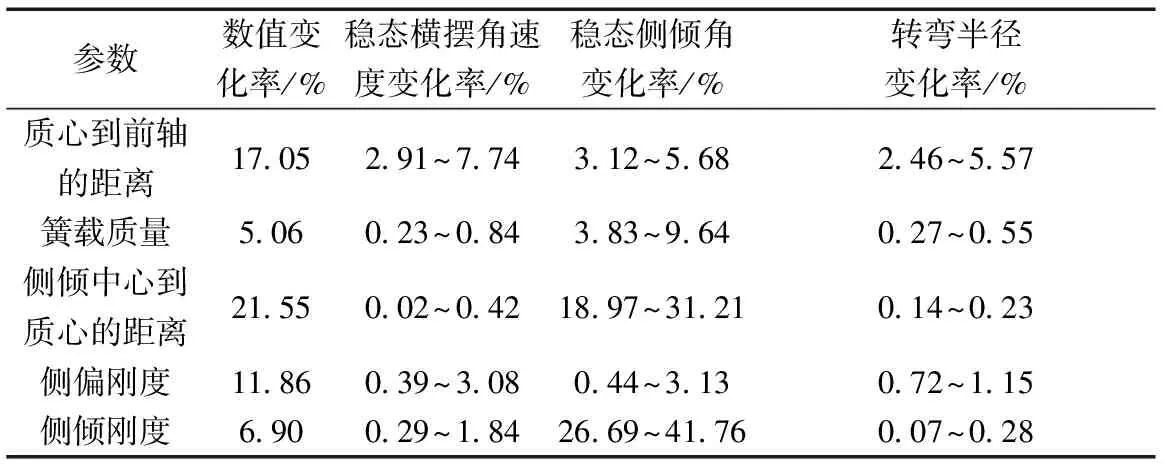
表2 角阶跃输入瞬态响应仿真试验数据
5 结论
以3自由度动力学模型和转向轨迹数学模型为基础,拖拉机方向盘转角为输入量,对拖拉机转向系统进行仿真试验,得到了其在变结构参数下的横摆角速度曲线、侧偏角曲线和行驶轨迹曲线,分析得到以下结论。
(1)随着速度变大、质心到前轴的距离增大及轮胎侧偏刚度增大,横摆角速度变大,拖拉机行驶稳定性变差;随着速度变大和质心到前轴的距离增大,拖拉机的稳态侧倾角加大,拖拉机更容易侧翻;侧倾中心到质心的距离和簧载质量的变化对拖拉机的横摆角速度影响较小,但对侧倾角的影响较大。
(2)随着速度减小、质心到前轴的距离减小、簧载质量减小、轮胎侧偏刚度增大、侧倾中心到质心的距离增大及侧倾刚度增大,拖拉机的转弯半径更小,操纵性好。

