基于反激式变换器的锂电池组主动均衡电路
严 聪, 莫易敏*, 熊 巍,2
(1.武汉理工大学机电工程学院, 武汉 431600; 2.湖北工程学院机械工程学院, 孝感 432000)
随着能源需求与环境污染问题的加剧,能量密度高、循环使用寿命长、自然放电率低、无记忆效应的锂电池应用越来越广泛[1-2]。然而由于锂电池单体容量小,电压低,需将多节单体电池串联和并联构成电池组以满足实际使用需求[3-5]。由于现有的电池制造技术难以保持电池单体使用性能的一致性,且使用环境等影响因素会加剧不一致性[6],从而降低锂电池组能量利用率,严重时甚至会造成安全问题。因此,需设计均衡系统,对锂电池进行均衡控制,提高锂电池组单体电池间的一致性[7-8],增加电池组的循环使用寿命,并提高其工作的安全可靠性。
目前锂电池组的均衡电路拓扑结构可分为能量耗散型均衡(被动均衡)与非耗散型均衡(主动均衡)[9-10]。文献[11]采用主被动均衡混合方式,可实现电池组均衡,但均衡时间长且被动均衡会导致能量损耗,降低能量利用率。文献[12]提出基于多电感的均衡拓扑结构,能量只能在相邻单体间转移,需通过多次能量转移实现电池组均衡,均衡时间长。文献[13]提出一种混合式均衡拓扑结构,底层采用双向Buck-Boost电路,顶层采用反激式变换器电路,结构简单但均衡效率较低。参考文献[14-16]提出基于单电感或单DC-DC变换器或单电容的均衡拓扑结构,可实现电池组和单体电池间的能量交换,但均衡时间长,效率低。文献[17]提出一种基于附加电源的均衡电路,其结构简单但均衡时负载电压会有波动,且不适用于锂电池组静置或充电状态。文献[18]采用同芯多绕组结构,可实现非相邻单体能量转移,但均衡效率低耗时长。
鉴于目前锂电池组主动均衡多采用相邻单体间能量转移或单体与电池组间能量转移方式,所用均衡时间长,为有效改善均衡效率,综合上述多种均衡拓扑结构,提出一种基于反激式变换器的均衡拓扑结构,以耦合电感作为储能元件,高能量电池单体通过均衡模块将能量转移至其余电池单体。反激式变换器自身电气隔离,各均衡模块可同时工作。结构简单,易于实现模块化且能快速实现均衡是其主要优点,并通过建模仿真验证了该拓扑结构的有效性及高效性。
1 均衡拓扑结构与工作原理
1.1 均衡拓扑结构
提出的基于反激式变换器的锂电池组均衡拓扑主要由四节单体电池、4组耦合电感及若干金属氧化物半导体场效应晶体管(metal oxide semiconductor field effect transistor,MOSFET)组成,其均衡拓扑结构如图1所示。

图1 基于反激式变换器的均衡电路Fig.1 Equalization circuit based on flyback converter
图1中,BT1、BT2等表示电池单体,S1、S2等表示MOSFET管,Li,j(i=1,2,3,4;j=1,2)表示第i组耦合电感,j=1时为原边绕组,j=2时为副边绕组。该均衡电路共有4个均衡模块,耦合电感L1,1与L1,2构成均衡模块1,可实现BT1与BT2-BT2-BT4之间的能量交换;耦合电感L2,1与L2,2构成均衡模块2,可实现BT2与BT3-BT4之间的能能量交换;耦合电感L3,1与L3,2构成均衡模块3,可实现BT3与BT1-BT2之间的能量交换;耦合电感L4,1与L4,2构成均衡模块4,可实现BT4与BT1-BT2-BT3之间的能量交换。反激式变换器本身可以实现电气隔离,且各均衡模块有对应绕组,所形成的充放电回路是相互独立的,多个模块可以同时进行均衡,能够有效提高均衡效率。
1.2 均衡拓扑工作原理
基于反激式变换器的锂电池组均衡拓扑的均衡模块基本工作原理如图2所示。图2中,BTH和BTL分别表示高能量电池单体和低能量电池单体,以电池组由BTH向BTL充电为例进行说明:开关管S1导通、S2断开,电流从BTH流出,经变换器的原边绕组L1回到BTH负极,由于S2断开,副边回路中无电流,BTH释放电能转换为磁能存储在耦合电感中。开关管S1和S2均断开时,原边绕组L1内电流消失,副边绕组通过续流二极管与电池BTL形成回路,变换器中的磁能转换为电能释放,给BTL充电。
反激式变换器工作模式可分为断续电流模式(DCM)和连续电流模式(CCM):连续模式下峰值电流小,平均电流大,开关管损耗小,但原边电感过大会影响负载电流变化响应速度,且系统不稳定;断续模式下,副边峰值电流大约为连续模式电流的2~3倍,对负载电流变化响应速度更快且系统非常稳定[19]。因此,所设计反激式变换器工作模式为断续电流模式。反激式变换器拓扑如图3所示,VH、VL表示高能单体电压和低能单体电压,L1、L2为一组耦合电感。工作在断续电流模式下流过耦合电感原边、副边绕组的电流波形图如图4所示。图4中,i1和i2表示流过L1和L2的电流,I1max和I2max表示其最大值。
设耦合电感原边绕组与副边绕组的匝数为N1和N2其匝比为N1∶N2=1∶1,原边绕组励磁电感(L1)与副边绕组励磁电感(L2)的大小均为Lm,开关管开关频率为f,占空比为D,周期为T。开关管S1导通至DT时刻,此时原边绕组电流线性上升,S1关断后,副边绕组电流线性下降,下降至Te(Te≤T)时刻,电流降为0。
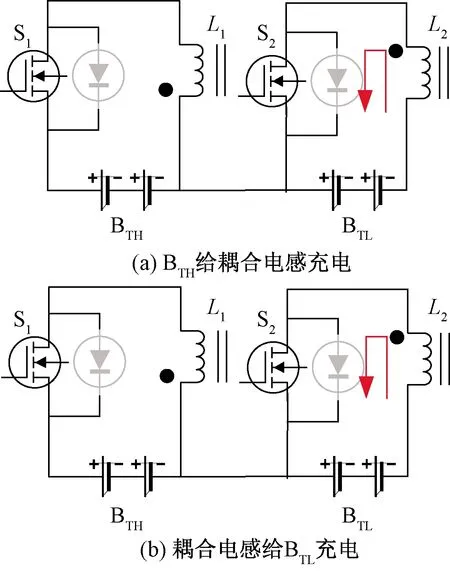
图2 均衡模块工作原理图Fig.2 Working principle diagram of the balance module
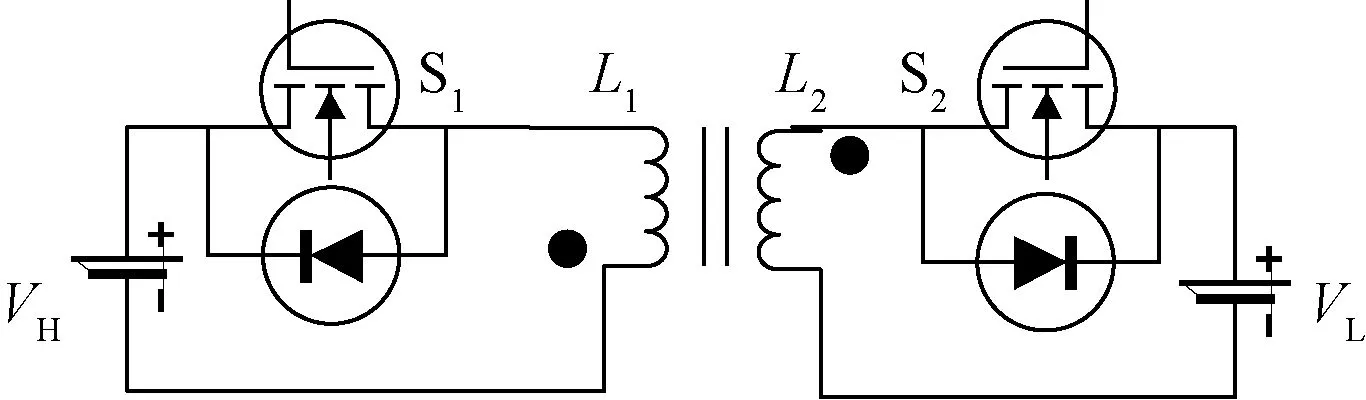
图3 反激式变换器拓扑结构Fig.3 Flyback converter topology

图4 耦合电感原边、副边绕组电流波形图Fig.4 Coupling inductance primary and secondary current waveform
当0≤t≤DT时:

(1)
当DT≤t≤Te时:
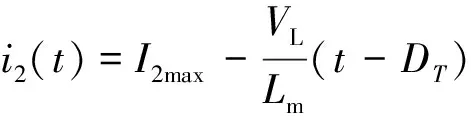
(2)
当t=DT时,原边绕组电流值与副边绕组电流均达到最大,可分别表示为

(3)

(4)
当t=Te时,i2(Te)=0时可得
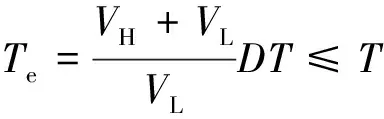
(5)
因此有
(6)
1.3 均衡拓扑控制策略
在均衡电路控制中,常用均衡变量有锂电池单体电压、电池荷电状态(state of charge,SOC)以及电池容量。以锂电池单体荷电状态SOCi(i=1,2,3,4)作为均衡变量,均衡开启条件为
Δ=max{SOCi}-min{SOCi}>0.05
(7)
式(7)中:Δ表示电池组中最高能量单体与最低能量单体间的SOC差值。若满足式(7),则开启均衡,比较相邻单体间的SOCi,以下列策略进行均衡。
比较SOC1与SOC2:若SOC1>SOC2,S1工作,BT1给BT2-BT3-BT4充电;若SOC1 比较SOC2与SOC3:若SOC2>SOC3,S3与S5工作,BT2给BT3-BT4充电,BT1-BT2给BT3充电;若SOC2 比较SOC3与SOC4:若SOC3>SOC4,S7工作,BT1-BT2-BT3给BT4充电;若SOC3 为验证所建立的基于反激式变换器的锂电池组均衡电路的可行性与高效性,将其与传统的多电感均衡电路和基于双层Buck-Boost均衡电路进行仿真对比。传统多电感均衡电路拓扑如图5所示,以电感作为储能元件,可实现相邻单体电池间的能量转移;基于双层Buck-Boost均衡电路拓扑如图6所示,分为内层均衡电路和外层均衡电路,其以两个单体电池为一组,内层通过电感实现组内相邻单体电池间的能量转移,外层通过电感实现组间电池组能量转移。 图5 传统多电感均衡电路Fig.5 Traditional multi-inductor equalization circuit 图6 双层Buck-Boost均衡电路Fig.6 Double-layer Buck-Boost equalization circuit 在MATLAB/Simulink中搭建仿真模型,单体电池标准电压为3.7 V,容量为2 Ah,4个单体的荷电状态SOC初始值分别为90%、85%、80%、75%,单体电池容量为2 Ah,分别对锂电池组静置、以0.3 ℃倍率充电和以0.6 ℃倍率放电三种状态进行仿真。仿真时,各电感、耦合电感允许最大电流不超过6 A。各均衡电路元件主要参数分别如表1所示。 静置状态下3种均衡电路的SOC随时间变化曲线图如图7所示。仿真结果表明,3种均衡电路均能实现锂电池组在静置状态下的均衡,均衡时间分别为158.711、458.152、232.050 s。 表1 各均衡电路元件主要参数表 图7 静置状态下SOC变化曲线Fig.7 SOC change curve under static state 由图7可知,3种均衡电路在静置状态下的过程分析可知:对于基于反激式变换器的均衡电路,在0~61 s内,4个均衡模块同时工作,能量快速从BT1、BT2转移至BT3、BT4;61~150 s内,均衡模块1、4工作,BT2与BT3可等效于静置,能量从BT1转移至BT4,由于仍有两个模块同时工作,此时仍可保持较高均衡效率;150~159 s内,均衡模块1工作,能量由BT1转移至BT2、BT3和BT4,此时由于4个单体SOC差异很小,因此,尽管均衡效率有所下降,但均衡耗时短。 对于传统多电感均衡电路,0~240 s内,3个电感同时工作,可等效于能量从BT1转移至BT4,由于能量只能单向传递且经过了3次转移,因此均衡效率低,此过程中BT2与BT3的SOC因转移过程中的能量损耗略有下降;240~458 s内,3个电感均工作,此时等效于将BT1、BT2中能量较高者转移至BT3、BT4中的能量较低者,由于BT1与BT2交替向低能量单体充电,因此均衡效率降低、耗时长。 对于双层Buck-Boost均衡电路,在0~120 s内,3个电感同时工作,此时可等效于能量从BT1转移至BT4,由于BT1可通过内层和外层均衡来转移能量,因此相较于传统多电感均衡电路均衡效率有所提高;120~232 s内,电感L3工作及外层均衡电路工作,能量从BT1-BT2转移至BT3-BT4,由于能量只经过一次传递,因此其均衡效率相较于传通过电感电路较高。 以0.3 C倍率给电池组充电状态下3种均衡电路的SOC随时间变化曲线图如图8所示。仿真结果表明,3种均衡电路均能实现锂电池组在充电状态下的均衡,均衡时间分别为158.325、454.688、230.996 s。 图8 充电状态下SOC变化曲线Fig.8 SOC change curve under charging state 由图8可知,3种均衡电路在充电状态下的过程分析如下。对于基于反激式变换器的均衡电路,在0~58、58~149、149~158 s 3个时间段内4个均衡模块的工作状况与上述静置状态时工作状况一致。此时由于对电池组进行充电,在58~149 s内BT2和BT3的SOC持续上升。对于传统多电感均衡电路,在0~240、240~455 s两个时间段内各电感的工作状况与上述静置状态时工作状况一致。此时由于对电池组进行充电,在0~240 s内BT2和BT3的SOC持续上升;240~455 s内,BT1、BT2的均衡放电电流与充电电流大小相等,因此其SOC基本不变。对于双层Buck-Boost均衡电路,在0~119、119~231 s时间段内各电感的工作状况与静置状态时保持一致。此时由于对电池组进行充电,在0~191 s内,BT2和BT3的SOC持续上升;119~231 s内BT1和BT2的均衡放电电流大于充电电流,因此SOC持续下降。 图9 放电状态下SOC变化曲线Fig.9 SOC change curve under discharging state 以0.6C倍率给电池组放电状态下3种均衡电路的SOC随时间变化曲线图如图9所示。仿真结果表明,三种均衡电路均能实现锂电池组在放电状态下的均衡,均衡时间分别为159.799、461.618、233.328 s。 由图9可知,3种均衡电路在放电状态下的过程分析可知,对于基于反激式变换器的均衡电路,在0~58、58~151、151~160 s时间段内4个均衡模块的工作状况与上述静置状态时工作状况一致。此时由于对电池组进行放电,在58~151 s内BT2和BT3的SOC持续上升。 对于传统多电感均衡电路,在0~243、243~462 s两个时间段内各电感的工作状况与上述静置状态时工作状况一致。此时由于对电池组进行放电,在0~243 s内BT2和BT3的SOC持续下降;243~462 s内,BT3、BT4的均衡充电电流小于放电电流,因此其SOC持续下降。 对于双层Buck-Boost均衡电路,在0~121、121~233 s时间段内各电感的工作状况与静置状态时保持一致。此时由于对电池组进行放电,在0~191 s内,BT2和BT3的SOC持续下降;119~231 s内BT3和BT4的均衡放电电流略大于充电电流,因此SOC基本保持不变。 由上述3种均衡电路在静置、充电、放电状态下的仿真结果及过程分析可知,3种均衡电路均能实现电池组均衡功能,降低单体电池间的差异性。从而避免某一优先充满能量或优先释放完能量而导致的整个电池组无法继续充电或放电的状况发生。 且提出的基于反激式变换器均衡电路相较于传统多电感电路和基于双层Buck-Boost均衡电路,其在整个均衡过程中均衡充放电电流最大。因此,在整个均衡过程中,基于反激式变换器的均衡电路均衡效率最高,基于双层Buck-Boost均衡电路均衡效率次之,传统多电感均衡电路均衡效率最低。 3种电路在电池组处于不同状态时,所用均衡时间均有差别。相较于静置状态,在充电状态下3种电路的均衡时间均有所缩短,分别为0.386、3.464、1.054 s。造成这种差异的原因是对电池组充电会使得单体电池电压上升,从而使得均衡电流变大,提高均衡效率。但因为均衡时间短,电压上升幅度较小,因此这种差异不大。在放电状态下3种电路的均衡时间均有所增加,分别为1.088、3.466、1.278 s。造成这种差异的原因是对电池组放电会使得单体电池电压下降,从而使得均衡电流减小,降低均衡效率。但因为均衡时间短,电压下降幅度较小,因此这种差异不大。 (1)介绍了基于反激式变换器的均衡电路,以耦合电感作为储能元件,对该电路进行了工作原理分析,并制定相应控制策略。同时,对反激式变换器工作单电流断续模式下进行了分析。 (2)搭建了均衡电路仿真模型,对锂电池组静置、充电及放电三种状态进行仿真,验证了该均衡电路及控制策略的可行性。将其与传统多电感均衡电路和基于双层Buck-Boost均衡电路对比,仿真结果表明在三种状态下所提出的均衡拓扑电路所用均衡时间最短,效率最高。2 仿真试验结果及分析


2.1 静置状态仿真及过程分析


2.2 充电状态仿真及过程分析
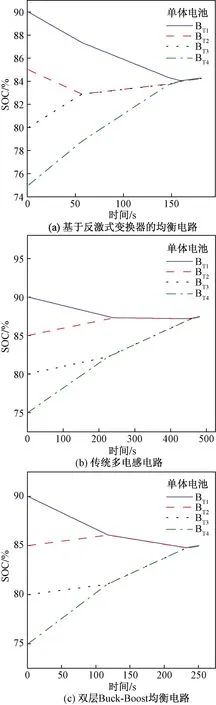
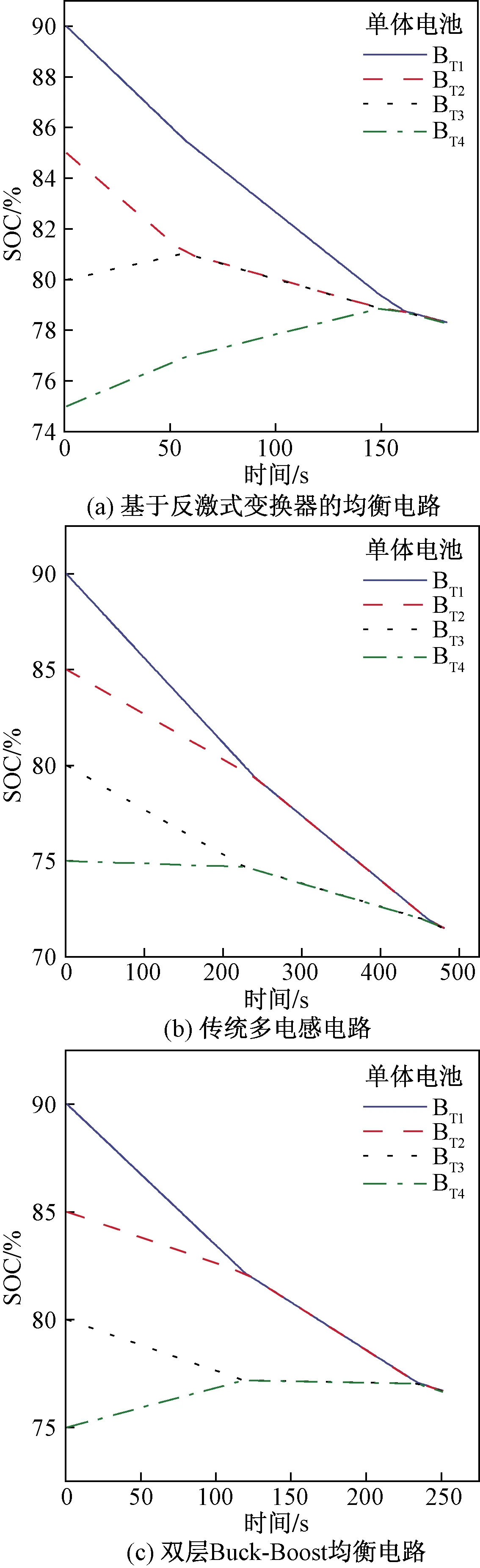
2.3 放电状态仿真及过程分析
2.4 结果分析
3 结论

