电磁波测距边长归算到高斯投影面上方法探讨

陈维燕，蔡林红，曹 强

(浙江省工程物探勘察设计院有限公司，浙江 杭州 310005)

在目前的工程测量中，边长是由电磁波在地球自然表面观测的斜距，出于建立控制网等目的，长度值应该归化至标石间的水平距离[1]，因而要进行一系列的改正。这些改正大致可以分成三类：一是仪器系统误差的改正；二是大气折射率变化所引起的改正；三是归算改正[2]。本文主要探讨归算方面的改正。

1 斜距归算至大地线长度

电磁波测距测得的长度是连接地面两点间的直线斜距D，由于受大气折光的影响，实际视线应为S，r为波道的曲率半径，β为波道曲率半径夹角[3]，如图1所示。大地点Q1和Q2的大地高分别为H1和H2，现要求大地点在椭球面上沿法线的投影Q1′和Q2′间的大地线长度s。

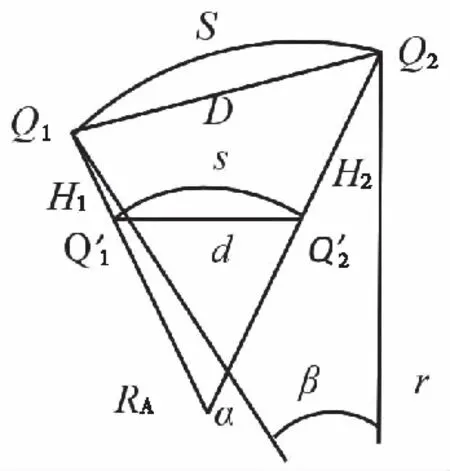
图1 斜距归算到参考椭球示意图

1.1 S-D的归算

由已知资料可知，

(1)

展开级数后，得：

(2)

式中,可令r=4R[4]。当S=10 km时，式(2)中第二项约等于0.06 mm，第三项几乎为0，考虑到实际工作中，边长一般不会超过10 km，故可以认为S=D。

1.2 D-d的归算

在三角形Q1Q2O中，根据余弦定理可知：

D2=(H1+RA)2+(H2+RA)2-2(H1+RA)×(H2+RA)cosα

(3)

(4)

(5)

带入式(4)可得：

(6)

将式(6)带入式(3)可得：

(7)

1.3 d-s归算

由已知公式可知：

(8)

展开泰勒级数后，得：

(9)

当S=10 km时，式(9)中第二项约等于1 mm，第三项几乎为零，故式(9)可简化为：

(10)

式中,

(11)

至此，即完成了斜距至参考椭球大地线长度的归算。

式(10)经过进一步简化，又可写成：

(12)

式中，

Δh=H2-H1

(13)

Hm=(H2+H1)/2

(14)

从式(12)可以看出,斜距归算至大地线长度可分成三项，第一项是由于测线两端的高差引起的倾斜改正，经过此项改正，测线已变成平距；第二项是由于平均测线高出参考椭球面而引起的投影改正，经过此项改正，测线已变成弦线；第三项是由弦长归化成弧长[5]。

2 大地线长度归算至高斯投影面

大地线长度s归算完成后，现要计算其在高斯投影面上的平距D1,如图2所示。

图2 大地线长度归算至高斯投影面上示意图

由控制测量可知：

D1=ms

(15)

式中，m为长度比。可按下式计算：

m=(m1+4mm+m2)/6

(16)

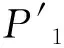
(17)

(18)

平均值为：

(19)

将式(17)、(18)代入式(15)、(16)，可得：

(20)

式中，

ym=(y1+y2)/2

(21)

Δy=y2-y1

(22)

Rm=(RA1+RA2)/2

(23)

式(20)可用于一等测量计算，对于二等测量有式(24)：

(24)

对于三等测量有式(25)：

(25)

至此，就完成了电磁波测得的斜距值至高斯投影平面的归算改正。

根据已有的研究成果，只要Hm的取值在0±6.4 m范围内即可[6]。考虑到我国克拉索夫斯基椭球的高程异常最大为65 m，全国范围平均为29 m，1975年椭球的高程异常全国范围平均为10 m，因此我国高程异常在0±6.4 m的区域，进行高程归化时，Hm可用正常高计算。当精度要求不很高时，在我国任何地区，Hm都可用正常高计算。

RA具体取值为按纬度、方位及椭球元素在《一、二等基线测量细则》的附表“任意法截弧曲率半径计算用表”中查取[7]。但在实际应用中，RA所允许的偏差大小与测距边平均高程面相对于投影面的高程Hm的绝对值的大小成反比。若以测区的平均高程面为投影面，取1 km已是不太可能出现的极端情况,却仍允许RA有40 km的偏差。因此我国任何地点、任何方位的区域性椭球的曲率半径均在6 370 km±40 km以内,完全没有必要再按纬度、方位及椭球元素作形式上的严格计算。在实际计算中，RA值为6 370 km足以满足精度的需要[8]。

3 在实际中的应用

下面举例说明上述公式在实际中的应用。

在A、B点上进行距离测量，仪器直接测得的距离S=1 753.02 m。A、B点的假定坐标分别为(105 260.45,104 219.49,60.25)，(103 670.88,103 480.33,30.42)。

计算过程：

(1)斜距归算至大地线长度

将S代入式(13)、(14)得：

Δh=H2-H1=29.83 m

Hm=(H2+H1)/2=45.34 m

代入式(12)，RA取6 370 km，可得

即斜距归算至大地线长度为1 752.76 m。

(2)投影改正

根据式(21)、(22)，可得：

ym=(y1+y2)/2=103 849.91 m

Δy=y2-y1=739.16 m

将第(1)步计算出的大地线长度s代入式(20)，Rm取6 370 km，可得：

即观测的距离归算到高斯投影面上的距离为1 752.99 m。

4 结 论

本文主要探讨了归算改正的基本原理、计算公式及相关参数的取值。由前文的叙述可以看出：

(1)若测量精度要求不高，或者边长较短且高差不大的情况，两点间的平距可由仪器观测的斜距直接计算得出，不必进行改正[9]；若测量精度要求较高，应按照式(12)，首先，将斜距归算成测线平均高程面上的平距，然后，将平距进行高程归算至参考椭球面上，最后，按照式(20)归算至高斯投影面上[10]。在实际计算时，Hm一般取正常高，RA取6 370 km已完全能够满足精度的需要。

(2)根据本文及之前的研究成果，我国高程异常在0±6.4 m的区域，进行高程归化时，Hm取正常高即可满足高精度测量要求；当精度要求不是很高时，在我国任何地区，Hm都可用正常高计算。但本文及之前的研究未探讨高程异常在0±6.4 m外的区域进行高精度测量计算时Hm的取值问题。

(3)电磁波测距边长归算到高斯投影面上，之前已做了一定的研究，与先前发表的研究成果比较，本文侧重基本原理的介绍、进行计算公式的推导并结合实际应用进行了过程演示。

(4)本文从理论上推导出了电磁波测距边长归算到高斯投影面上的严密计算公式，并探讨了在实际计算中相关参数的取值，有一定的理论和实用意义。

(5)进一步研究本课题，能够更加明确其基本原理和相关参数的选取，提高测量精度。