基于Excel-VBA的公路线路坐标正反算程序设计

钟宏斌，刘庆元

(1.中南大学 地球科学与信息物理学院，湖南 长沙 410083；2.长沙市轨道交通集团有限公司，湖南 长沙 410009)

在公路与铁路工程建设中，测量进场后首要工作就是线路放样要素的计算。Excel作为常用的办公软件具有较强的数据处理和编辑排版能力，它的公式、函数变化万千、应用广泛，但几乎没有在测量工程线路坐标正反算中应用。本文根据多年生产实践和多个高速公路项目的实际工作经验，编写的基于Excel-VBA自定义函数的线路坐标正反算程序，可实现与Excel的公式、函数融合应用。

1 Gauss-Legendre通用公式

公路工程线型构型复杂多变，但都是由直线、圆曲线和缓和曲线三种基本曲线组成[1-2]。本程序采用通用Gauss-Legendre公式[3-6]，可适用于这三种曲线。

1.1 曲线元上任意点处切线方位角的计算

文献[3]已给出曲线元上任意点处切线方位角的计算公式：

(1)

式中，α为待求点切线方位角;αA为线元起点A处切线方位角;G为线元的偏转系数;ρA为线元起点A处曲率;l为待求点至起点A处曲线长;ρAB为线元起终点的曲率差;LS为线元长度。

其中G的取值为1、-1或0，当曲线元左偏时，G=-1；线元右偏时，G=1；线元为直线时，G=0。

1.2 曲线上任意点的坐标计算公式

文献[3]、[4]已给出线元任意点坐标计算的Gauss-Legendre通用公式：

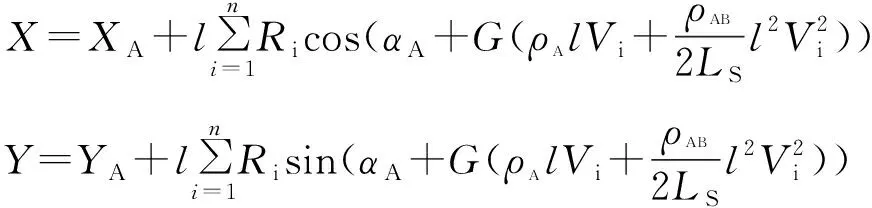
(2)

式中,X、Y为待求点坐标;XA、YA为线元起点A坐标。

文献[4]指出，当节点数n=5时，式(2)即可满足工程中所有的线路构型的坐标计算精度要求。5节点公式中Ri、Vi的值为：R1=R5=0.118 463 442 5;R2=R4=0.239 314 335 2;R3=0.284 444 444 4;V1=1-V5=0.046 910 077 0;V2=1-V4=0.230 765 344 9;V3=0.5。

将Ri、Vi的值代入式(2)，可用于计算线元上任意点的坐标，即线路中桩坐标。

边桩坐标的计算公式如下：

(3)

式中，B为边桩到中桩的距离(左边距为负,右边距为正)。

式(2)、(3)为线路任意点坐标计算的Gauss-Legendre通用公式。

2 基于Excel-VBA的线路坐标正反算程序实现

本程序基于Excel-VBA，将曲线要素数据库直接录入于工作表，计算过程以代码封装于VBA[7]，使用方法以函数的形式交由用户，其程序运行流程图如图1所示。

图1 程序运行流程图

2.1 构建曲线要素数据库

在空白工作表中构建如表1所示表格格式(第一行为表名，第五行为表头，第六行开始是线元数据，J3单元格输入线元个数；有效数据输入列为A-J列)。

为保证程序的正常运行，作如下约定：(1)表格结构须与表1一致；(2)要填写正确的线元个数；(3)起点方位角单位为度(不能是度分秒的格式)，并保留尽量多的小数位数；(4)本工作表表名可以按需命名。

表1 曲线要素数据库格式

根据设计提供的《直线、曲线及转角一览表》，计算、提取线元要素，填写曲线要素数据库的工作表，将工作簿命名存盘。

2.2 坐标正算函数主程序

程序以自定义函数[8]的方式驱动，故主程序为函数，定义两个函数名，其格式为：(1)坐标正算X坐标函数：ZSX("工作表名",里程,偏距)；(2)坐标正算Y坐标函数：ZSY("工作表名",里程,偏距)。注意函数中工作表名要用英文双引号引起来。主程序实现以下功能：

(1)判断用户输入的里程、偏距和工作表名(即曲线要素数据库表名，下同)，提取相应曲线要素。实现代码[9-10]：

nCount = Sheets(WorksheetName).Cells(3, 10).Value

Fori= 1 TonCount

If Mileage >= Sheets(WorksheetName).Cells(i+ 5, 2).Value And Mileage <= Sheets(WorksheetName).Cells(i+ 5, 3).Value Then

ForJ= 1 To 9

quxian(J) = Sheets(WorksheetName).Cells(i+ 5,J+ 1).Value

NextJ

Nexti

(2)调用坐标正算子程序计算，返回结果至单元格。

2.3 坐标正算子程序

坐标正算子程序采用5节点Gauss-Legendre通用公式，中桩坐标计算实现代码：

r(0) = 0.118 463 442 5:r(4) =r(0):r(1) = 0.239 314 335 2:r(3) =r(1):r(2)=0.284 444 444 4

v(0) = 0.046 910 077:v(4) = 1 -v(0):v(1) = 0.230 765 344 9:v(3) = 1 -v(1):v(2) = 0.5

Pi1 = Application.WorksheetFunction.pi()

Length1=Abs(MyMileage1-MyArray1(1))

resultsX1= MyArray1(3)

resultsY1= MyArray1(4)

Fori= 0 To 4

IntegralItem1 = MyArray1(5) + MyArray1(9) * (v(i) * Length1 / MyArray1(7) +Length1 ^ 2 * v(i) ^ 2 * (1 / MyArray1(8) - 1 / MyArray1(7)) / (2 * MyArray1(6)))

resultsX1 = resultsX1+ Length1 *r(i) * Cos(IntegralItem1)

resultsY1= resultsY1+ Length1 *r(i) * Sin(IntegralItem1)

Nexti

2.4 线路切线方位角计算程序

定义主程序函数：ZSA("工作表名",里程)。在函数中判断用户输入的里程和工作表名，提取曲线要素，调用切线方位角子程序进行计算，将结果返回至单元格。切线方位角子程序实现代码：

Length1 = Abs(MyMileage1 - MyArray1(1))

Azimuth1 = MyArray1(5) + MyArray1(9) * (Length1 / MyArray1(7) + (1 / MyArray1(8) - 1 / MyArray1(7)) * Length1 ^ 2 / (2 * MyArray1(6)))

2.5 坐标反算程序

定义函数名：FSSlantDistance("工作表名",大概里程,X坐标,Y坐标)。坐标反算程序用于根据坐标反算里程、偏距，为防止因为多值问题(多由回头曲线、水滴型曲线等特殊曲线线型产生)，需用户提供大概里程(如无多值问题，大概里程可以随意赋值，只要不超过线路里程范围即可)。采用迭代法计算，以大概里程为里程初始值，以用户输入的坐标到大概里程的中桩坐标所在线路法线的距离为迭代值，迭代直至该距离为无穷小。实现过程如下：

(1)根据用户输入的大概里程ProbablyMileage，调用坐标正算程序，求得该里程中桩坐标CalX、CalY和切线方位角，并计算出切线方位角的法向方位角VerticalAzimuth。

(2)计算待求点(X,Y)到点(CalX、CalY)沿VerticalAzimuth方向的距离DeltaSlantDistance。实现代码：

DeltaSlantDistance = (Y- CalY) * Cos(VerticalAzimuth) - (X- CalX) * Sin(VerticalAzimuth)

(3)判断DeltaSlantDistance值大小：

若值足够小，则求出点(X,Y)到点(CalX、CalY)的距离OutputSlantDistance1，返回反算结果(里程：ProbablyMileage，偏距OutputSlantDis-tance1)，跳出循环；

若值过大，以ProbablyMileage + DeltaSlantDistance作为新的大概里程，返回步骤(1)，进入下一循环。

实现代码：

If Abs(DeltaSlantDistance) < 10 ^ (-8) Then

OutputSlantDistance1 = ((Y- CalculationY) ^ 2 + (X-CalculationX) ^ 2) ^ 0.5

A1= VerticalAzimuth + 90 * PI / 180

X1= CalculationX:Y1= CalculationY:X2 =X1+ cos(A1):Y2 =Y1+ sin(A1)

If (Y1 -Y) * (X2 -X) - (X1 -X) * (Y2 -Y) > 0 Then OutputSlantDistance1 = -OutputSlantDistance1

Else

ProbablyMileage = ProbablyMileage + DeltaSlantDistance

End If

步骤(1)、(2)、(3)均在循环体内，以上代码省略了循环体。

至此，线路坐标正反算的程序已具备相应功能。

3 算 例

下面，以某项目的一段线路直曲表为例，验证编写的线路坐标正反算程序(以下称本程序)正确性。设计提供曲线要素如表2所示。

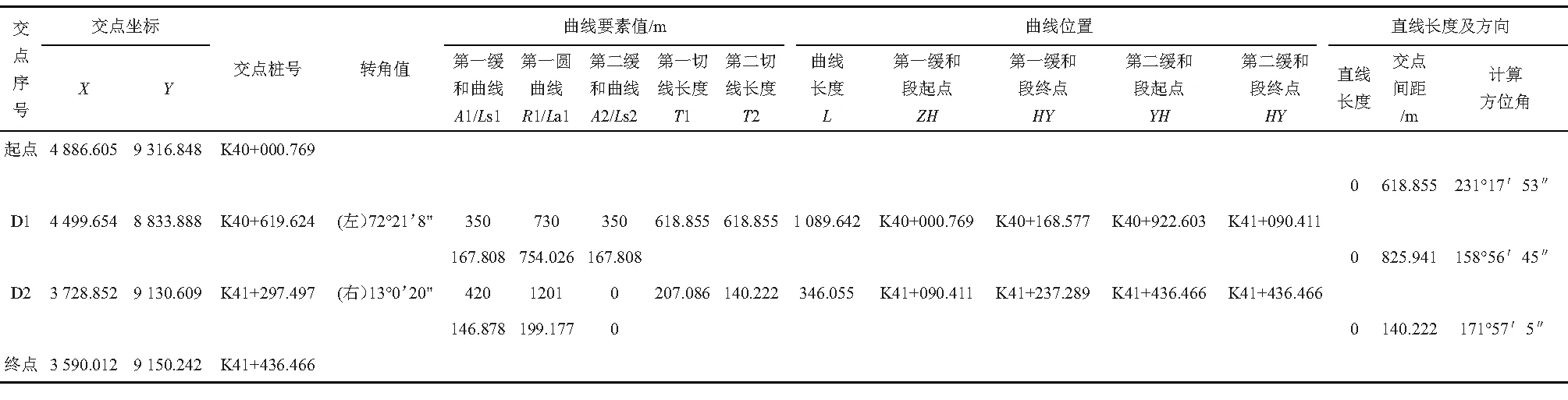
表2 直线、曲线及转角表

将表2的曲线要素按线元法录入曲线要素数据库，并存于名为“右平”的工作表中。因该线路所有线元均以相切衔接，即下一线元起点坐标、方位角为上一线元终点坐标、方位角，故在录入要素时，部分要素可用本程序直接计算。直线段半径为无穷大，则半径填接近于无穷大的数即可，如1090。所有曲线要素内容如表3所示。

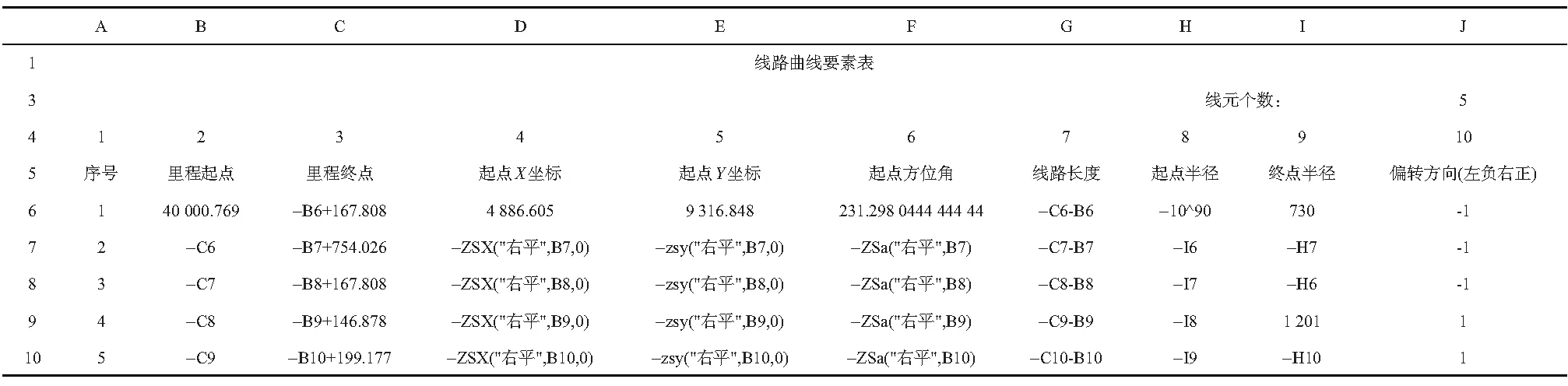
表3 程序曲线要素数据库工作表数据录入表

计算结果即为完整的曲线要素表，如表4所示。

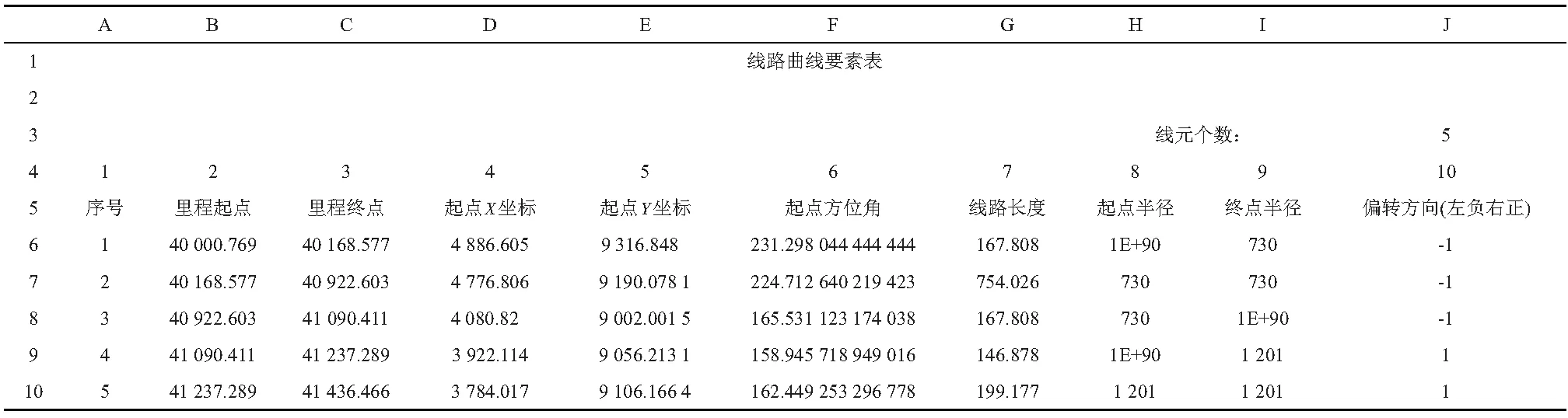
表4 程序曲线要素数据库工作表计算结果表

根据线元法的特性和以上曲线要素录入方法，若某个线元出错，则线路终点坐标、方位角必然出错，故只需复核线路终点的坐标、方位角即可。程序计算结果与设计对比如表5所示。

由表5可知，本程序计算结果与设计几乎一致，其误差因设计《直曲表》精度低于本程序小数点保留位数引起。

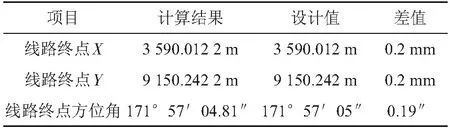
表5 程序曲线要素数据库计算结果复核表

下面以里程K40+900右偏5 m为例，验证程序计算边桩坐标正确性。正算中桩坐标、方位角：X=4 102.790 0;Y=8 996.693 8;α=167.305 173 179 975°。手算与本程序计算结果对比如表6所示。

表6 程序边桩坐标正算计算结果复核表

由表6可知，边桩坐标正算结果正确无误。下面用坐标正算程序来验证坐标反算。其对比表如表7所示。

表7 程序坐标反算计算结果复核表

由表7可知，坐标反算的里程、偏距与正算时赋值一致，故坐标反算程序计算正确。

笔者在多个项目的应用中，也验证了本程序计算正确、精度达到施工要求。

4 结 语

随着科技的进步，测量仪器越来越先进，电脑与仪器的交互功能越来越强大、方便。本程序最大的优势在于：(1)通过电脑计算的线路坐标，按照仪器所需的格式进行编排，可方便的导入仪器；(2)从仪器导出的数据可在电脑上按施工和竣工要求进行更多数据编辑处理任务；(3)特别是在现代测量过程中，坐标计算、数据处理、格式转换都需要与Office软件相结合，以达到数据流无阻碍的流动，形成我们需要的各种数据报表和应用格式。基于Excel-VBA自定义函数的公路线路坐标正反算程序，采用Gauss-Legendre通用公式来统一计算模型，界面简洁明了，通俗易懂；可以计算直线、圆曲线、缓和曲线甚至包括不完全缓和曲线等类型线元，覆盖了工程施工过程中所有的线路形式，功能强大、计算精度高。将计算程序转为Excel自定义函数，与Excel自身功能融为一体，可随意调用，便于排版，便于与其他软件、仪器交互；简洁的函数输入，避免了普通线路坐标计算程序繁琐的操作过程，加快了操作速度。基于Excel-VBA自定义函数的公路线路坐标正反算程序，可以给测量人员、施工管理人员节省时间，提高工作效率，改善程序使用体验，适合于目前工程测量中数据的日常计算和批量处理。