投影梯度算法求解非线性反问题的αl1-βl2正则化

赵祝光，丁 亮

(东北林业大学)

0 引言

该文考虑求解(1)式的非线性算子方程

A(x)=y,

(1)

其中x是稀疏的，A:l2→Y是l2和Y之间的非线性映射，Y为Banach空间，其范数为‖·‖Y.在实际问题中，由于误差的存在，精确数据y不能预先得到，所观测的数据yδ往往带有扰动或噪声，y与yδ满足‖y-yδ‖≤δ，其中δ为噪声水平.通常求解(1)的方法有lp(p≥1)稀疏正则化[1-4].然而lp(p≥1)正则化有时无法提供最稀疏的解，因此提出非凸lp(0≤p<1)稀疏正则化作为其替代方法.关于l0稀疏正则化，可参考文献[5-8].在最近5年里，αl1-βl2正则化在稀疏恢复领域已经引起了很大关注[9-13].作为lp(0≤p<1)的一种替代，函数

α‖·‖l1-β‖·‖l2(α≥β≥0)

具有较好的性质，它是l0-范数一种较理想的近似.从计算的角度来看，该函数具有比l0更简单的结构.在文献[9]中，作者研究了形式为

(2)

的正则化的适定性和收敛速度，其中A是有界线性算子，

Rα,β(x)=α‖x‖l1-β‖x‖l2,α≥β≥0,q≥1.

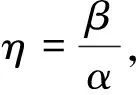
其中，

Rη(x)=‖x‖l1-η‖x‖l2,α>0,1≥η≥0.

特别地，当q=2，文献[9]提出了求解问题(2)的ST-(αl1-βl2)算法：

(3)

其中，sk为步长，λ>0.与经典的迭代软阈值算法类似，ST-(αl1-βl2)算法结构简单，容易实现.然而，ST-(αl1-βl2)算法可以任意慢，因此构建ST-(αl1-βl2)算法的加速方法是有意义的.文献[14]通过拓展投影梯度算法求解问题(2)，提出了算法(3)的两个加速替代方法，分别为基于广义条件梯度方法的投影梯度算法和基于替代函数的投影梯度算法.而该文的主要目的是将前一种投影梯度算法进行推广.用基于广义条件梯度方法的投影梯度算法求解非线性不适定反问题的非凸αl1-βl2稀疏正则化.该文选择投影梯度方法有两个原因，首先，它的表达式简单并且容易实现，另一个原因是它收敛得相当快，因此足以解决大规模不适定问题.

该文结构为：第一节为预备知识.在第二节中给出求解αl1-βl2稀疏正则化的基于广义条件梯度方法的投影梯度算法.第三节给出确定l1-球约束半径R的方法，并证明算法的稳定性.

1 预备知识

该文主要通过下列正则化方法来求解非线性不适定反问题(1)：

α‖x‖l1-β‖x‖l2,α≥β≥0 .

(4)

定义

(5)

假设1 令非线性算子A:l2→Y满足如下条件：

(1)A是有界的.

(2)A有连续的Fréchet导数.

(3)A′(nn)*y→A′(x*)*y对于所有的y成立.

定义1 如果x†∈l2满足

A(x†)=y,

Rη(x†)=min{Rη(x)|x∈l2,A(x)=y},

则x†称为问题(1)的Rη-最小范数解.

定义2 如果supp(x)={i∈N|xi≠0}，则x∈l2称为稀疏的，其中xi是x的第i个分量.对于s∈N，如果‖supp(x)‖0=s，则x∈l2为s-稀疏.

定义3 (Morozov偏差原则)对于1<τ1≤τ2，选择α=α(δ,yδ)>0使得

定义4 对于给定的α>0，软阈值算子被定义为

其中ei=(0,…,0,1,0,…)，xi是x的第i个分量，并且

定义5 在l1-球上的投影定义为

接下来回顾文献[15]中关于软阈值算子和投影算子之间关系的两个结果，关于参数α和R的关系，参考文献[15，Fig.2].

引理1 对于可数指标集Λ，记lp=lp(Λ)，1≤p<∞.对于任意固定的a∈l2(Λ)并且α>0,‖Sα(a)‖l1是一个分段线性的、连续的、关于α的递减函数.此外，如果a∈l1(Λ)，则‖S0(a)‖l1=‖a‖l1，并且当α≥maxi|ai|时，有‖S0(a)‖l1=0.

引理2 如果‖a‖l1>R，则a在半径为R的l1-球上的l2投影PR(a)=Sα(a)，其中选择α使得‖Sα(a)‖l1=R成立.如果‖a‖l1≤R，则PR(a)=S0(a)=a.

引理4 设H是内积为〈·,·〉、范数为‖·‖H的希尔伯特空间，对于任意x∈H，PR(x)被刻画为H中的唯一向量，使得

〈w-PR(x),x-PR(x)〉≤0,∀w∈BR.

此外，投影PR是非扩展的，即

∀x′,x″∈H.

2 基于广义条件梯度方法的投影梯度算法

其中

Φ(x)=Θ(x)+α‖x‖l1-β‖x‖l2,

算法1陈述了ST-(αl1-βl2)算法，算法1的收敛性见定理1，其详细证明可见文献[16，定理4.8].

算法1 (有限维空间中问题(4)的ST-(αl1-βl2)算法)

(1)选择x0∈Rn，并且设k=0.

(2)如果xk=0，那么

(3)否则，确定下降方向zk，使其满足

(4)确定步长sk，使其满足

(5)令xk+1=xk+sk(zk-xk)，k=k+1，返回第三步.

接下来给出问题(4)的一阶优化条件.

成立，上式等价于

对于所有z∈l2，t∈[0,1]成立.因此可以得到

当t→0+时，引理得证.

算法1中关键的一步是zk的获取，使其满足

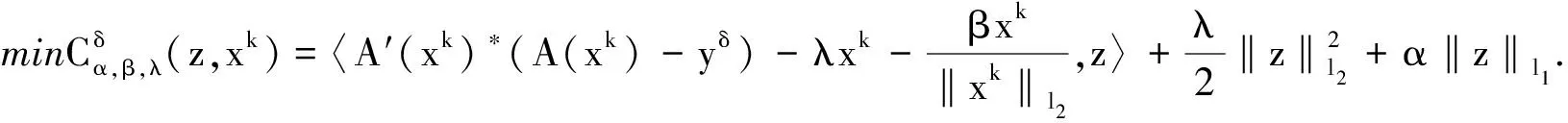
(6)

文献[2]通过下列式子求解问题(6)：

(7)

然而，(7)收敛地任意慢，为了加速ST-(αl1-βl2)算法，该文将(6)转化为下列形式的约束优化问题：

(8)

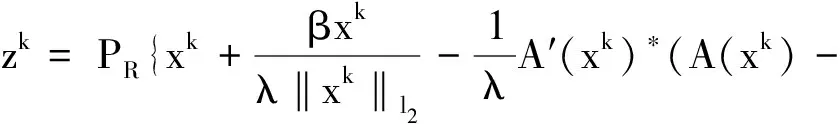
(9)

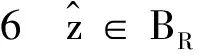
(10)

对于任意λ>0成立，(10)等价于

(11)

且f′(0+)≥0与(11)是等价的.

接下来给出具体的投影梯度算法.

算法2 (问题(4)的投影梯度算法)

(1)选择x0∈Rn，并且设k=0.

(2)如果xk=0，那么

(3)否则，确定下降方向zk，使其满足

yδ)).

(4)确定步长sk，使其满足

(5)令xk+1=xk+sk(zk-xk)，k=k+1，返回第三步.

3 半径R的确定

从前面的讨论可以知道，对于某个R，问题(6)和(8)是等价的.在开始迭代(9)之前，需要选择一个恰当的R，特别在实际应用中，R的选取对于计算是十分重要的.该节通过Morozov偏差原则给出一个确定l1-球约束半径R的方法.

所以一个关键的问题是如何检查问题(8)中的R是否合适.因为存在一个与R相关的正则化参数α，使得(6)与(8)等价，所以确定一个恰当的R，需要检验与之对应的正则化参数α取值是否正确.通过引理1与引理2，只知道α是一个分段线性、连续、关于R的递减函数，并且α与R之间没有显式公式，所以不能直接从R的值得到α的取值，因此无法确定R是否正确.

另一种方法是考虑Morozov偏差原则.对于任意给定的R，可以检验正则化参数α是否满足定义3，即

算法3 (在Morozov偏差原则下，问题(4)的投影梯度算法)

(1)选择x0∈Rn，R0∈R+，并且设j=0，

k=0.

(2)如果xk=0，那么

(3)否则，确定下降方向zk，使其满足

(4)确定步长sk，使其满足

(5)令xk+1=xk+sk(zk-xk),k=k+1.

(6)如果xk满足Morozov偏差原则(定义3)，设Rj+1=Rj+c,c>1，否则停止迭代.

(7)j=j+1，返回第三步.

最后在Rn中考虑算法3的稳定性.

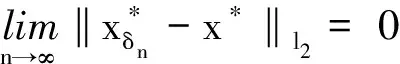
即

(12)

4 结论

该文针对非线性不适定问题，研究了αl1-βl2,α≥β≥0型罚项的非凸稀疏正则化问题：

α‖x‖l1-β‖x‖l2.