基于准反向变异的实数笛卡尔遗传编程算法
付安兵,魏文红,张宇辉,郭文静
(东莞理工学院计算机科学与技术学院,广东东莞 523808)
(*通信作者电子邮箱weiwh@dgut.edu.cn)
0 引言
笛卡尔遗传编程(Cartesian Genetic Programming,CGP)[1]是一种基于图结构的遗传编程,不同于传统的基于树形结构的遗传编程,基于图结构的遗传编程具有处理多个输入和输出的能力。1997 年,在进化数字电路的技术中第一次描述了和CGP 相关的方法,但CGP 真正出现是在1999 年,到2000 年时它作为一种新的遗传编程被正式提出[2]。自那以后,CGP就不断被全世界各地的学者研究和改进,并被成功用于不同的领域。2009 年,Gajda 等[3]将CGP 用于多态电路的门级优化;2005 年,Harding 等[4]将CGP 用于机器人控制器的进化;2010 年,CGP 被Khan 等[5]用来进化神经网络,后来又被Gadja等[6]用来进化高效数字电路;2015年,Vasicek[7]用CGP来做组合数字电路的优化,到了2016 年,Vasicek 等[8]又用它来做电路的近似模拟。另外在图像处理领域,Harding[9]于2008 年将CGP 用来做图片滤波器的进化;Sekanina 等[10]在2011 年将CGP 用来做图像处理;2015 年,Paris 等[11]又将CGP 用于自学习的图像滤波器。在生物信息学领域,CGP 同样有着重要的应用,如Ahmad等[12]在2012年利用基于CGP进化的人工神经网络进行乳腺癌的检测。当然CGP 的应用远不止于此,近年来越来越多的CGP 改进算法在不同领域发挥着重要的作用[13]。
在CGP 不断被研究改进的过程中,许多CGP 变种算法也相继被提出。Walker 等[14]提出了Modular CGP(MCGP),MCGP 允许模块(Modules)能执行创建、进化、重用、删除等操作,而且Walker 等的研究也表明,在解决和数字电路相关的问题中,MCGP 的解通常优于CGP。Harding 等[15]提出了自修改函数的概念,同时将自修改操作基因加入到基因库中,由此产生了自修改笛卡尔遗传编程(Self-Modifying Cartesian Genetic Programming,SMCGP)算法。在SMCGP 算法中,染色体的长度不是固定的,它可以根据自修改操作基因的表达与否而动态地改变自身结构,对于一些特定问题,SMCGP 相较其他CGP 变种算法有更高的收敛速度以及更优的解。另外,Turner 等[16]于2014 年提出了循环笛卡尔遗传编程算法(Recurrent Cartesian Genetic Programming,RCGP),打破了CGP 有向图不能存在循环连接的限制,在RCGP 的图中,节点之间的连接不再受到限制,可以与任何一个节点连接(包括它自己)。实验表明,在一些不能完全观测的任务中,RCGP 具有更好的表现。2007年,Clegg等[17]采用浮点数表示基因的方式,提出了另外一种CGP 的变种——实数笛卡尔遗传编程(Real-Valued Cartesian Genetic Programming,RVCGP)算法,并在该算法中第一次成功地引入交叉操作算子。
在对CGP的研究过程中发现,CGP的变异手段太过单一,进化算法本身过于简单,因此本文提出了一种基于准反向变异的实数笛卡尔遗传编程算法(ADvanced Real-Valued Cartesian Genetic Programming algorithm based on quasi oppositional mutation,AD-RVCGP)。在AD-RVCGP 中,利用准反向变异算子和末端变异算子并结合反向个体的信息进行变异操作,在对符号回归问题的求解中,对比其他三种常见的CGP 变种算法,本文算法在收敛速度以及解的精度等方面的表现明显优于其他三种算法。
1 实数笛卡尔遗传编程
1.1 RCVCGP编码背景
与CGP 一样,RVCGP 也采用图结构进行非循环有向图的表示,图中的节点由一个函数基因和一组连接基因构成;不同之处在于CGP采用整数表示一个基因,而RVCGP中的每个基因则是由一个大于0 小于1 的浮点数表示。图1 显示了一条染色体编码的例子。RVCGP 被提出的初衷是为了将交叉算子加入到该算法中,研究表明在RVCGP 中引入交叉算子后,其性能表现要优于传统的笛卡尔遗传编程算法[18]。另外,采用浮点数表示基因的方式使得基因的变异粒度更小,并能以更缓慢的速度影响个体的表现,因此与CGP 跳跃式的变异过程相比,RVCGP的变异过程显得更加平滑。
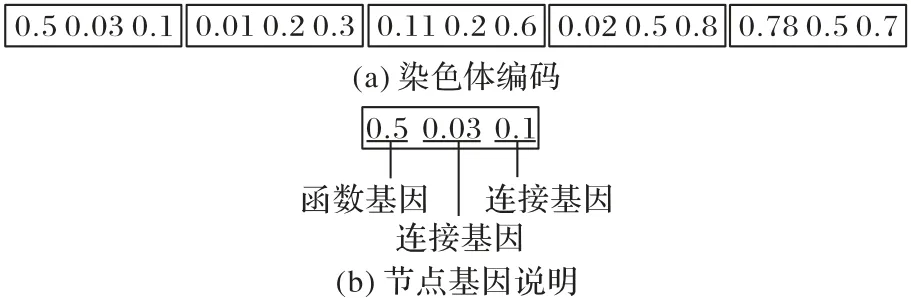
图1 RVCGP中的染色体示意图Fig.1 Schematic diagram of a chromosome in RVCGP
1.2 RVCGP编解码
由于RVCGP 的基因采用浮点数表示,所以从RVCGP 基因编码到非循环有向图的构建需要进行一个如下的解码过程。
假设函数表中有n个函数,节点的函数基因为g,则其在函数表(事先决定的用于算法的一系列函数集合,如常用的加减乘除等)中的索引由式(1)给出;同样假设一条染色体共有m个节点,某个连接基因为c,则其对应的连接节点索引由式(2)给出。

其中:Ig表示该函数在函数表中的索引,Ic表示该连接节点在染色体节点集合中的索引;floor 表示向下取整函数。一个完整的解码过程如图2 所示,假设算法用到的函数集合为FUNC,它包含{+,-,*,/}这四个函数,算法输入变量个数为2,分别用x1、x2表示,输出变量个数为1,用o表示。从图2 中可以看出,节点的序号从2 开始,那是因为算法含有两个输入,即两个输入节点分别占有编号0 和1,在图中并未画出它们,但这并不影响算法的具体实现,因为当处理到连接节点序号为0 或者1 的时候就知道它表示的是算法的输入参数。节点2 的函数基因为0.2,连接基因分别为0.02 和0.56,该节点代表的函数在函数表中的索引为floor(4*0.2)=0,那么该节点的函数为加法函数,它的两个输入参数分别来自节点0(floor(2*0.02)=0)和节点1(floor(2*0.56)=1)的输出,即第一个输入变量x1和第二个输入变量x2,那么该节点的输出就是x1+x2。同样对于节点3 而言,其函数基因为0.31,则该函数在函数表中的索引为floor(4*0.31)=1,减法函数为该节点的函数,它的连接基因分别为0.7 和0.41,表示节点2(floor(4*0.7)=2)和节点1(floor(4*0.41)=1)的输出为该节点函数的输入,该节点的输出是节点2 的输出x1+x2减去节点1 的输出x2,即x1。以此类推,最终可得到如图2 所示的完整的计算图结构,整个算法的输出o是:x1*x1。从图2中还可以看出,节点5 没有连接到输出节点,因此它的输出对整个计算图的输出不产生影响,这种对输出不产生影响的节点称为非激活节点,其他节点称为激活节点。激活节点和非激活节点并非一直不变的,随着算法演进,激活节点可以变成非激活节点,非激活节点同样也可以变成激活节点。研究表明,在CGP 中大量非激活节点的存在有助于提高算法的性能[18]。
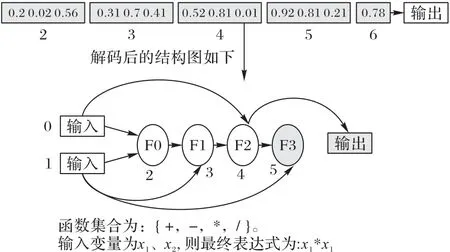
图2 完整计算图结构Fig.2 Structure of complete computation diagram
RVCGP 采用1+λ的进化策略,每次迭代都选择一个当前最优个体作为父代,通过变异的手段生成λ个子代个体,然后对子代个体进行适应性评估,当子代存在某个个体适应值优于父代个体适应值时,将该子代个体替换为父代用于下一代繁殖。另外,当子代存在的最优个体的适应值等于父代个体的适应值时,也将用该最优子代个体替换当前父代,因为该子代个体已经累计过足够多的变异,有利于后续的进化。进化算法的终止条件可分为达到最大预设繁殖代数停止或达到一定的误差值停止两种方式,前者是在迭代了一定代数后结束进化过程,后者是当进化过程中出现最优个体适应值满足一定误差条件后停止算法的迭代。
1.3 CGP在工程上的应用
CGP 最早是一种用于进化数字电路设计的算法,但同时CGP 也是基于图结构的算法,因此它和神经网络有着很好的适应关系。因此,近年来随着神经网络的发展,就有学者将CGP 和神经网络结合起来解决一些工程上的实际问题,如引言提到的用于乳腺癌检测的基于CGP 的人工神经网络。另外相较于传统的神经网络学习算法,CGP 的一个明显优势是它不会陷入局部最优解,而且CGP 不仅可以学习调整神经元之间的权重参数,它还可以学习调整整个神经网络的结构,因此笛卡尔遗传编程算法用来训练神经网络相较传统的神经网络训练方法有更广泛的适用性。但如文献[19]提到的利用CGP 进行卷积神经网络的进化时,其需要花费比学习传统算法更多的时间才能达到较好的效果,而且随着神经网络层数的增多,其花费的时间通常是不可接受的,因此该算法主要应用在一些相对较浅的神经网络结构中。
2 AD-RVCGP
2.1 准反向变异背景
一般在进化算法的种群初始化,大都选用随机的方式初始化种群,这样算法的收敛速度就具有极大的不确定性,如果种群初始化个体中有些个体离最优解个体距离(一般指欧氏距离)近,那么理论上算法应该能较快地寻找到最优解;反之,种群初始化个体都离最优解很远,那么理论上算法将进行大量的迭代才有可能找到最优解。这样的情况对采用1+λ进化策略的算法影响很大,因为采用1+λ进化策略的算法在每次迭代都是由一个最优父代个体生成λ个子代个体,相当于每次迭代都在初始化种群。为了弥补这种缺陷,本文提出了一种基于准对称点的变异算子,即准反向变异。准反向变异的概念与准对称点有着必然的联系,下面介绍准对称点的概念。
假设要寻找到的最优解处在区间(a,b),对于任意X∈(a,b),其对称点X′=a+b-X,对于X的对称点X′,有如下定理。
定理对于任意X∈(a,b),其对称点为X′,到最优解的距离函数为d(•),概率函数为P(•),则有结论:P(d(X′) <d(X))=0.5。
证明 如图3 所示,最优解可能分布在区间(a,X],(X,M],(M,X′],(X′,b)这四个区间。
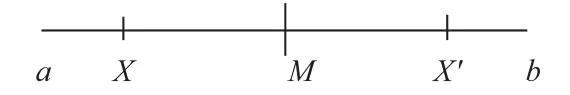
图3 准对称点的例子Fig.3 Example of quasi-symmetric points
最优解落到区间(a,X]和(X′,b)的概率相等,因为a到X和X′到b的距离相同,这时最优解位于区间(a,X]时,显然离X更近,而落到(X′,b)时,显然离X′更近。
同样,最优解落到区间(X,M]和(M,X′]的概率相同,而最优解位于区间(X,M]时,显然离X更近,落到区间(M,X′]时,离X′更近。
综上,最优解离X更近或者离X′ 更近有着相同的概率,即P(d(X′) <d(X))=0.5,得证。
这样直接对X取其对称点X′,从概率上来说X′离最优解更近的概率不会比X离最优解近的概率大,准对称点的提出改变了这种现状。
准对称点 对任意X∈(a,b),X的对称点为X′,关于X的准对称点Xopp由式(3)给出:
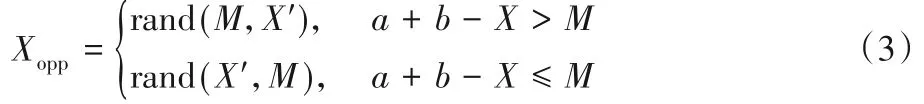
式中:M代表(a,b)的中点,rand(x,y)表示区间[x,y]中的随机数。
在文献[20]中,已经证明了对于X的准对称点Xopp,它离最优解更近的概率比X离最优解更近的概率大。
2.2 准反向变异和末端变异
除了运用CGP 原始的单点变异算子,本文还提出了两种变异算子,分别为准反向变异和末端变异。在准反向变异中,对于一个基因g,如果它被选中变异,那么取g的准对称点作为突变后的基因gmut,gmut的值由式(4)给出。
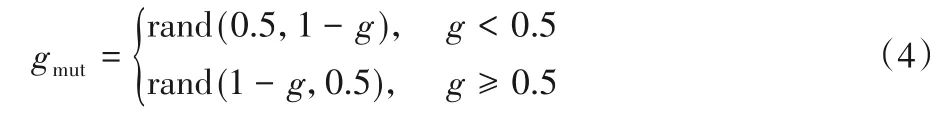
准反向变异的伪代码在算法1给出。
算法1 准反向变异。
算法1 中的G表示染色体所包含的基因集合,算法遍历整个基因集合,按照一定的概率选择基因进行准反向变异操作,其中,rand(x,y)表示x和y之间的一个随机数,Gk表示基因集合中第k个基因的值。
在单点变异算子和上述的准反向变异算子中,因为每个基因都有变异的概率,因此需要对每个基因进行遍历,这样对于含大量基因的染色体个体而言将花费大量的计算时间,其时间复杂度为O(n),n为染色体基因的长度。因此本文提出了一种只对输出节点进行变异的变异算子,即末端变异,该变异通过只对输出节点进行变异,能明显减少计算的时间,其时间复杂度为O(1)。而且,通过改变输出节点对应的输入,也能有效地改变个体的输出,特别是在输出节点前已经有了大量节点相互连接的情况下,仅通过输出节点变异能极大地利用前面节点的累积的变异成果。
2.3 反向个体
在RVCGP 中,每一个个体可以由一条包含多个节点的染色体所标识,每个节点又由多个基因构成。节点的连接基因决定了节点之间的连接结构。对于一个个体的反向个体,有如下定义。
反向个体 对于一个个体M,对应的染色体X,除去X的输入和输出节点后,将X中的激活节点变为非激活节点、非激活节点变为激活节点而形成的新染色体X′对应的个体M′被称为M的反向个体。需要注意:一个个体的反向个体不止一个,因为变化后的激活节点之间的连接方式不止一种。反向个体生成算法由算法2给出。
算法2 反向个体生成算法。
算法2 的主要功能是将一个个体中的激活节点和非激活节点的状态进行置换,算法先遍历整个染色体包含的节点集合,将非激活节点加入到集合activeNodes中(它们将被变为激活状态),随后遍历集合activeNodes中的每个激活节点为其设置连接节点。
2.4 AD-RVCGP描述
传统的CGP 采用1+λ的进化策略,通常取λ=4,每一次迭代都是一个最优父代仅通过变异的手段生成4 个子代个体,然后对这4 个个体进行适应性评估得到其适应值,如果子代个体中存在其适应值不差于父代个体的适应值,则用该子代个体取代父代个体进行下一次的迭代。在这个进化过程中发现,会出现很多代的迭代都不会有优于父代的子代个体出现,这时候可能目前的最优个体已经陷入了局部最优解,因此本文提出了一种基于准反向变异的RVCGP 算法。预设了一个参数t,当t次迭代之后都没有比父代更优的个体出现时,下一次迭代用当前父代的反向个体进行变异生成子代个体。整个AD-RVCGP由算法3给出。
算法3 准反向变异进化算法。


其中:maxGeneration、maxHit、index、lowerImprovedCount、childrenSize、changeParentThreshold、muteParam分别表示算法最大迭代次数、算法最大命中次数、循环索引、未能找到优于当前最优个体的迭代次数、子代个体数、改变生成父代个体策略控制参数、子代变异方法选择控制参数。算法的终止条件有两个:一个是达到最大迭代次数maxGeneration,另外一个是算法运行过程中命中次数达到预设数值maxHit。算法最外层的循环代表迭代次数,每一次循环代表产生新一代种群,这个生成过程通过一定策略选择父代进行单点变异以及算法2 的准反向变异手段产生子代,然后进行适应性评估,接着选取优于父代个体的最优子代个体作为当前最优个体。值得注意的是,当算法在一定的迭代次数后仍未能有比当前个体更优的个体出现时,算法会选择用当前最优个体的反向个体作为父代进行下一代种群的生成。
2.5 AD-RVCGP收敛性分析
采用保留最优个体的进化算法在理论上是能保证算法的收敛性的,遗传编程虽不同于传统的进化算法,但算法还是有保留当前最优个体的操作(最优父代变异产生子代,而且子代中优于当前父代的个体将被选为最新父代)。因此,ADRVCGP在理论上是收敛的,下面给出简要证明。
定义搜索空间为S={Li|节点数为N的节点列表集合,Li节点中的基因g∈(0,1)},其中N为事先给定的染色体节点数。在S上定义适应值函数f:S→R。则AD-RVCGP 的任务是在S中寻找至少一个适应值最优的个体L*,使得f(L*)=max{f(L):L∈S}。考虑S中的任意两个个体L1和L2,显然当采用变异手段时,从L1通过变异的手段得到L2的概率p是一个大于0的数。因为L1和L2都是一个等长的包含实数元组的列表,因此它们之间是可以仅通过变异操作来改变实数元组的值实现互相转换的。
设S*={L∈S|f(L)=f*}表示取得全局最优的个体集合,考虑算法执行到第k代,每个个体的变异概率为pm,每一代产生的个体数为n,这样到第k代时一共有k*n个个体被选择变异,而且对于这些个体中的每一个,发生变异后属于S*的概率为pc=pm*p,p的含义和上面任意两个个体转换的概率相同。由于采用了最优个体保留的策略,因此在这k*m个个体中只要有一个属于S*,就有Ek=0,Ek代表第k代当前最优解和真实最优解之间的误差,从而得到P(Ek=0) ≥1-(1-pc)k*n,另外对∀ε>0,有1 ≥P(Ek≤ε) ≥P(Ek=0) ≥1-(1-pc)k*n。对上式取极限有,即得limk→∞P(Ek≤ε)=1,因此算法以概率1 收敛到全局最优。
3 实验与结果分析
为了将本文算法和传统的CGP 进行性能比较,主要用到5 个符号回归问题(表1)进行测试。符号回归问题主要是从一些给定的输入-输出对样本中找到一个将自变量和因变量相关联的数学表达式。在解决以上问题时,将分别用笛卡尔遗传编程(CGP)、实数笛卡尔遗传编程(RVCGP)、自修改笛卡尔遗传编程(SMCGP)以及本文所提的AD-RVCGP 进行实验测试。其中,在文献[21]中,研究表明第三个函数用传统的CGP 很难对该问题进行求解,得出了传统CGP 在平均进行大约55 万次迭代才能找到该表达式。为了进行实验测试,一些参数需要被确定,如节点个数、最大迭代次数、函数集合、输入集合等。在本次实验中,传统CGP的参数由表2给出,RVCGP参数由表3 给出,SMCGP 参数由表4 给出,AD-RVCGP 参数由表5 给出。其中,在CGP 中有一个Level-back 的参数,该参数限制了每个节点能和它相连接的最前面的节点位置,如Level-back取5,则每个节点只能和其前面5个节点进行连接。由式(2)可以看出,从RVCGP 到CGP 的转换后,RVCGP 的每个节点都可以连接到它前面的任意节点,因此在实验中对CGP 的参数取19,另外为了保证测试公平,由于本文提出的进化算法不完全和传统CGP 的进化算法一致,所以本文算法的子代个体数设置为10,而其他3 种算法的则设置为20。对于个体适应值,本文选择算法对每个样本自变量的输出和样本真实输出之差的绝对值的累计误差,即:

其中:Otrain代表每个样本的输入对应的算法输出;Osample代表样本的真实输出;n代表样本数。因此个体的适应值越小,则代表其适应性越好,本文的目标是使得最优个体的适应值变得越来越小,直至趋于0。除此之外,还新增了一个评估参数“hit”[22],它表示当算法对于单独的一个样本的输出与其真实值之间的误差的绝对值小于0.01 时,则代表一次命中。因为这时对于当前样本的预测值和真实值之间的差异已经很小了,在函数图像上表现为这两个点几乎是重合的,另外实验主机CPU 为Intel i5-8400,内存大小为16 GB,磁盘大小为500 GB,操作系统为Windows 10专业版。

表1 符号回归函数Tab.1 Functions of symbolic regression
基于表2~5 对应的算法参数分别利用CGP、RVCGP、SMCGP 和AD-RVCGP 对表1 的五个符号回归函数进行测试,每个符号回归问题都测试100 次,四个算法分别都最多迭代10 000 次,然后统计成功找到表达式的次数、失败的次数、成功的次数中平均迭代的次数、成功找到表达式所花费的平均时间(单位:s)、最差命中次数,实验结果如表6所示。

表2 传统CGP参数Tab.2 Parameters of traditional CGP
AD-RVCGP、CGP、RVCGP、SMCGP 算法在表1 中的函数的符号回归实验中迭代2 000次时,算法的收敛效果分别如图4~8所示(总共进行了100次实验)。

表3 RVCGP的参数Tab.3 Parameters of RVCGP

表4 SMCGP的参数Tab.4 Parameters of SMCGP

表5 AD-RVCGP的参数Tab.5 Parameters of AD-RVCGP

表6 不同算法的符号回归测试性能对比Tab.6 Performance comparison of different algorithms in symbolic regression test
从图4~8的收敛效果来看,AD-RVCGP在所有表1中的函数的符号回归测试的表现均优于CGP、RVCGP 以及SMCGP算法。另外从表6 的实验数值结果来看,AD-RVCGP 的成功次数比其他三个算法都要多,而且其平均迭代次数、平均花费时间也是四个算法中最少的,在失败的案例上,AD-RVCGP最差命中次数是四个算法中最多的,因此可以看出,即使在未能成功找到表达式的情况下,AD-RVCGP 找到的表达式也是更接近真实表达式的。另外SMCGP 算法在解决本次实验所提问题时,它是四个算法中表现最差的,不仅需要花费比其他算法多得多的迭代次数,而且还存在很多次失败的结果,这可能跟SMCGP 的染色体节点数是动态的因素有关,每次进化过程中,SMCGP 算法的变异操作不仅包括常用的单节点变异,还包括修改染色体节点的操作,如增加、删除、替换染色体的节点等,因此该算法需要花费的时间较多,另外染色体节点最大数参数也会对算法的性能造成影响。

图4 函数x6 -2x4 + x2收敛效果对比Fig.4 Comparison of convergence effect of function x6 -2x4 + x2

图5 函数(x3 + x)/2收敛效果对比Fig.5 Comparison of convergence effect of function(x3 + x)/2

图6 函数(x2 + x+2)/2收敛效果对比Fig.6 Comparison of convergence effect of function(x2 + x+2)/2

图7 函数x5 -2x3 + x收敛效果对比Fig.7 Comparison of convergence effect of function x5 -2x3 + x
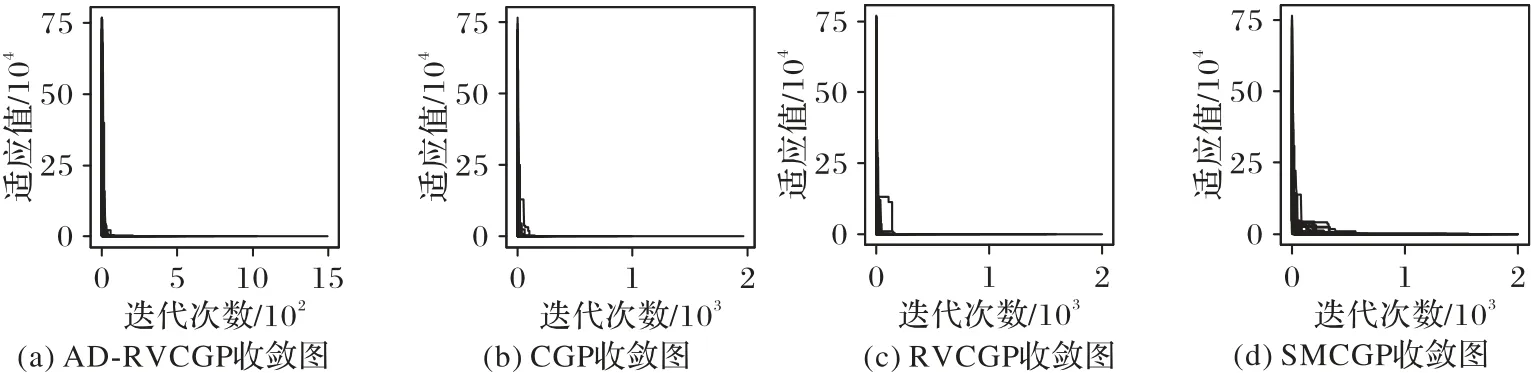
图8 函数x4 + x3 + x2 + x收敛效果对比Fig.8 Comparison of convergence effect of function x4 + x3 + x2 + x
4 结语
针对CGP 算法变异手段单一、进化方法过于简单等问题,本文提出了一种基于准反向变异的RVCGP 算法ADRVCGP。AD-RVCGP 利用准反向变异手段并结合反向个体的信息,将其用于算法的演进过程中。实验结果表明,ADRVCGP 相较CGP、RVCGP、SMCGP 有着更强的寻找最优解的能力,也具有更高的收敛速度和更优的求解精度。算法参数的选择对算法产生的影响需要进一步验证,如节点个数参数、变异选择参数、改变父代个体控制参数等参数的选择会对该算法的性能产生怎样的影响还不得而知,这也是接下来要进行的研究。另外,本文提出的反向个体的概念,目前也只是简单利用激活节点和非激活节点进行取反得出,更有创意的反个体概念也值得进行深入的研究。

