面向资源受限用户的高效动态数据审计方案

李秀艳，刘明曦，史闻博，董国芳*

（1.云南民族大学电气信息工程学院，昆明 650500；2.东北大学计算机科学与工程学院，沈阳 110819；3.东北大学秦皇岛分校计算机与通信工程学院，河北秦皇岛 066004）

（*通信作者电子邮箱dongguofang1@163.com）

0 引言

近年来随着物联网设备呈现爆炸式的指数增长，促使这些用户设备将其数据存储在云端来解决用户存储容量不足的问题。云存储为用户提供便捷的外包服务，它也是推动物联网的基础平台［1］，在物联网中大部分设备通常为轻量级设备，如智能仪器仪表（Intelligent Meter，IM）、智能手机、平板电脑、可穿戴设备等［2-3］。随着海量设备接入云端进行交互，这些受限设备的应用越来越广泛［4］。例如远程测控系统一般以用户端和工作站相结合的方式实现数据的自动测量及存储。用户端可以通过远程控制IM 来获取测量数据［5］，并将结果实时更新反馈到网络中，由于IM 可以作为网络中独立的节点存在，能采用就近原则与本地线缆进行网络连接，这样可以保证数据的实时传输。但由于设备本身存储和计算能力有限，需要通过网络将实时数据存储在云服务器中，用户再通过云服务器来获取所需的数据信息；并且不同的用户可以在同一时间对同一进程数据信息进行有效监测。为了给这类受限设备提供合适的存储和安全保护，面向资源受限用户设备审计应运而生，并成为密码学领域的一个研究热点。

随着物联网的进一步发展，网络技术、云计算等日新月异。大多数终端用户设备，如IM 为资源受限设备，其处理能力、通信能力及存储能力都非常有限［6-8］。为了使用户从沉重的高运算负担中解脱出来，用户数据外包得到快速发展，特别针对资源受限的用户，外包数据可以将用户繁重的计算任务外包给云服务提供商（Cloud Service Provider，CSP），并由CSP来向用户提供各种数据库服务，从而降低用户维护数据的成本［9］。但同时用户数据存储在半诚信的CSP 中，失去了对数据的直接控制，CSP 可能会由于软/硬件故障或为了自身利益等问题，返回不正确或不完整的检索结果给用户，并且当上述问题发生时，CSP 可能还会隐瞒用户，让用户以为数据依然被正确地存储在CSP 上，由此为确保访问信息的正确性和完整性，需要用户定期执行数据完整性验证［10］。此外为减轻用户的计算负担，可以通过引入代理来帮助用户在云存储审计方案中处理数据［11-12］。远程存储的数据不仅可以被访问，还应被用户端更新，如数据的修改、删除、插入等操作［13］。为保证现场测试实时数据的及时更新，以及用户从云服务器端可以实时获取更新信息来准确掌握监测数据的动态情况，需实现数据的高效动态操作请求。在远程测控场景下，数据信息需要进行保密，以防数据泄露导致利益损失；同时审计的安全性也应该被满足。

本文使用高效且安全的轻量级算法来构建一个适合轻量级设备自身特点，且综合考虑高效性、安全性的审计方案，主要工作如下：

1）基于新颖的计数布隆过滤器（Novel Counting Bloom Filter，NCBF）和多棵Merkle 哈希树（Multi-Merkle Hash Tree，M-MHT）技术提出一个高效且安全的数据结构NCBF-MMHT。其中：NCBF 用来支持数据的快速查找，实现审计高效性；M-MHT用来存储数据及确保数据的安全性。

2）提出一个针对资源受限用户设备的轻量级审计方案，对审计各实体采用不同的分配操作。首先引入代理帮助用户处理复杂的高运算过程；其次审计验证通过云服务器端返回的数据证据响应和代理端发送的标签证据来共同验证数据存储的完整性，并从协议上来实现对资源受限用户的轻量级审计。

3）通过安全分析和性能评估验证了本文方案的高效性与安全性，该方案能够保证审计结果的正确性和完整性。

1 相关工作

物联网和云计算领域的研究已成为热门，而数据完整性验证一直是外包物联网数据中一个非常重要的问题［3］。关于数据完整性验证的研究大致可分为隐私安全、动态更新和轻量级审计三个方面。

在2016 年，Botta 等［14］和Diíaz 等［15］提出了物联网和云计算集成想法，并讨论了关于物联网设备中存在海量数据急需外包到云服务器中进行处理的问题。为了保证数据的完整性，Ateniese 等［16］于2007 年首先提出了可证明数据拥有的概念，利用同态认证技术和随机样本技术来验证云中的数据的完整性。同年，Juels 等［17］提出了数据可检索性的概念，并利用点检和纠错编码技术设计了具体方案，这也是提出审计协议的开端。为了保证数据持有的公正性，Wang等［18］引入了第三方审计员（Third Party Auditor，TPA）。为了保护数据隐私，Wang 等［19］在2011 年使用同态加密技术解决数据隐私问题。到2013 年，Wang 等［20］又提出采用随机掩码技术来保护数据隐私的审计方案。同年，Yang 等［21］提出了一种基于配对加密的新方案来解决数据隐私问题，还利用数据碎片技术将每个数据块分割成扇区，减少了数据标签的数量，提高了审计性能。2016 年，Li 等［22］提出了一种基于零知识证明的隐私保护远程数据完整性审计方案。

为了支持数据的动态操作，Wang等［19］提出采用Merkle哈希树（Merkle Hash Tree，MHT）为数据结构的审计方案，该方案能支持块级的全数据动态操作。Zhu 等［23］提出了一种新的基于片段结构和索引哈希表（Index Hash Table，IHT）的审计方案。Liu 等［24］设计了一种基于MHT 高效细粒度更新的动态数据完整性审计方案，该方案支持对可变大小的文件块进行公共审计。Tian 等［25］提出了一种利用动态哈希表（Dynamic Hash Table，DHT）来支持数据动态更新的云存储审计方案。Yu 等［26］利用密钥更新技术解决了云存储审计中的密钥暴露问题。Shen 等［27］提出了一个基于位置数组双向链接信息表（Location Array-Doubly Linked Info Table，LA-DLIT）的动态数据结构实现公共审计协议，该协议采用全局和无块抽样验证方式，可以减少审计的计算和通信开销。

为了减轻用户的计算负担，提出了多种轻量级云存储审计方案。Li 等［28］提出了基于在线/离线签名的低端设备云存储审计方案，但用户仍然需要在联机阶段执行数据签名的计算。为了解决这个问题，Wang等［29］提出了一种基于身份的云存储审计方案，引入代理来帮助用户生成数据签名。在此方案中，用户不需要消耗计算资源来生成数据签名。Shen 等［30］设计了一种轻量级的云存储数据完整性审计方案，通过引入第三方媒介（Third Party Media，TPM）来代表用户处理数据。Zhang 等［31］提出了采用模糊不区分公共审计方案，该方案在TPA 上进行轻量级计算，并将大部分计算委托给CSP。Rabaninejad 等［32］提出了具有抗共谋性的数据审计方案，该方案在实时在线阶段为用户端提供轻量级的计算成本，用户将数据签名生成任务委托给一个专用代理，并提供身份数据隐私和抗共谋用户撤销。

2 问题描述与预备知识

2.1 系统模型

如图1 所示，本文考虑外包数据可验证场景，设计的方案由资源受限用户（Resource-constrained User，RU）、私钥生成器（Private Key Generator，PKG）、诚实代理人（Honest Proxy，HP）、第三方审计员（TPA）和云服务器（CSP）五个实体组成：1）RU是数据所有者，有将用户个体数据存储在云服务器上的需求。与TPA 和CSP 相比，用户端设备的计算能力更低。同时，用户的数据量很大，超出了用户的存储能力，需要通过CSP 为用户提供数据存储服务。2）PKG 是诚信的私钥分发中心，通过获取用户和代理人身份信息，然后返回用户私钥和代理私钥。3）HP 是诚信实体，有一定的存储和计算能力，负责帮助用户上传数据、生成签名及动态更新操作。4）TPA 是第三方可信组织，它代表用户执行云存储审计，可以定期检查云服务器上用户数据的完整性；而且对数据存在诚实好奇性，审计中需要保护数据隐私。5）CSP 是负责为用户提供云存储服务的半诚信实体，存储能力和计算能力强，但由于利益问题会存在共谋、泄露隐私等现象。

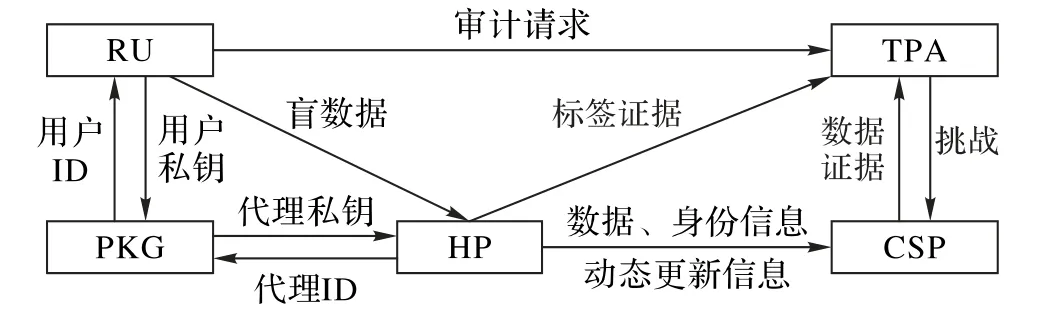
图1 系统模型Fig.1 System model

系统模型为资源受限用户设备实现轻量级审计方案，该方案的审计过程可描述如下：

1）初始化阶段：RU对数据进行简单的文件分块和数据致盲处理后将数据上传给HP，并删除本地数据。

2）数据上传阶段：HP 收到数据后为数据生成标签证据，接着使用布隆过滤器（Bloom Filter，BF）对数据进行存储分配，并指定到相应MHT 上，然后采用MHT 来对已分配数据进行存储，这样可以大大提升数据验证的查找速度。操作完成后HP将收到数据发送给CSP，由CSP存储用户数据。

3）审计阶段：当RU 有审计需求时，首先向TPA 提出审计请求，接着由TPA 向CSP发送审计挑战，并通过CSP返回的数据证据响应和HP发送的标签证据来验证数据存储的完整性。

4）动态更新阶段：RU 提出动态请求，并将动态请求和动态数据发送给HP；HP 生成新数据标识后，更新特定的数据结构；然后由HP 将动态请求和动态数据发送给CSP，CSP 收到后将动态请求放入工作记录表中，并更新数据。

2.2 威胁模型

在威胁模型中，假设TPA 是诚实但好奇的实体，CSP 是半诚实云服务器，在此情况下，云服务器可能向用户返回不正确或不完整的验证结果；或者由于利益关系出现与其他实体内部勾结泄露用户数据，导致用户端的经济损失。因此在存储和审计过程中，在各实体未知用户真实数据的情况下，需要帮助用户处理数据，安全的审计框架和数据结构是不可或缺的。

本文主要考虑两种类型的攻击：

1）内部攻击：内部敌手主要是半诚信的云服务器，在动态更新过程中，为了自身利益，不按照用户要求来更新数据块，试图返回不正当的检索结果达到欺骗用户的目的。

2）共谋攻击：主要是半诚实云服务器和诚实好奇的第三方审计员合谋获取用户隐私数据信息，从中谋取利益。

2.3 设计目标

本文方案的目的是实现高效和安全的外包数据检索验证，基于图1模型，本文设计实现以下安全目标：

1）公共审计：用户可以将审计任务委托给任何可信的第三方机构来执行。在可信第三方机构执行完审计任务后，只需将审计结果反馈给用户即可。

2）轻量级：方案支持资源受限用户的审计请求。即对用户运算能力和存储能力有限、无法完成确保数据安全的签名操作以及数据存储，需要用户以外的系统成员设备来负责完成。

3）动态操作效率：用户对云服务器存储数据的动态需求主要是进行插入、修改和删除，对于资源受限用户来说，这些动态更新的效率将直接影响用户对云端的存储需求，因为用户的计算能力非常有限，动态数据结构的检索时间复杂度直接关系到审计的执行效率，高效的动态数据结构才能满足资源受限用户的实现需求。

4）低延迟、计算开销小：通信开销和计算开销小，整个审计过程时延低，在用户请求动态操作和审计操作流期间，可以避免用户和TPA 多次与数据结构进行交互，快速获知操作结果。检索和更新速度越快，审计越高效，用户的经济损失也就越小。

5）数据隐私安全：用户在数据上传、动态更新和审计过程中，需要其他各实体在未获取真实数据信息情况下，帮助用户处理这些数据，确保用户数据信息的安全；而且由于用户不直接检查数据的完整性，同时也需确保将正确的审计结果反馈给用户。

2.4 预备知识

2.4.1 双线性映射对

双线性映射对［28］定义如下：存在G1、G2和GT是p阶素数乘法循环群，G1和G2分别是g1和g2的生成元，则双线性对e：G1×G2→GT具有以下几个性质：

1）双 线 性 性：对∀u∈G1，∀v∈G2和a，b∈Zp，有e(ua，vb)=e(u，v)ab成立。

2）可计算性：对∀u∈G1和∀v∈G2，存在有效的算法能够计算e(u，v)。

3）非退化性：对任意的g1和g2，存在e(g1，g2)≠1。

2.4.2 离散对数问题

对给定素数p阶的有限循环群G，其生成元g和任意元素h∈G，计算a∈Zp值是很困难的，使得h=ga。换句话说，对于任意一个概率多项式时间对手A，解决离散对数（Discrete Logarithm，DL）问题［33］的概率可忽略，即为：

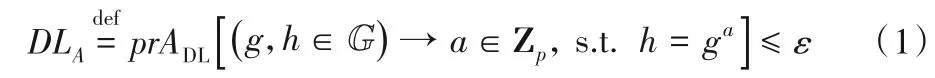
2.4.3 计算Diffie-Hellman密钥交换算法问题

令G为一素数阶p的循环群，对a随机选取一个生成元g和随机数a，b∈Zp，给定(g，ga，gb)∈G，计算其值gab是很困难的。也就是说，对于任意一个概率多项式时间对手A，解决计算Diffie-Hellman（Computational Diffie-Hellman，CDH）密钥交换算法问题［34］的概率可以忽略不计，即为：

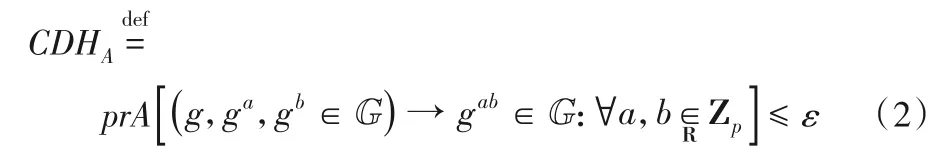
2.4.4 布隆过滤器

布隆过滤器（BF）［34］是一个对元素集合实现查询验证且存储高效的数据结构，不仅可以表示元素所在的集合，还可以支持数据的动态操作和查询，优势在于可以在时间复杂度为O(1)内有效地实现用户的查询请求。BF以实现n个元素的集合S查询，假设由长度为m的数组RBF表示，集合可表示为S={s1，s2，…，sn}，将元素通过k个相互独立的哈希函数H={h1，h2，…，hk} 映射到数组RBF中去，每个哈希函数的范围都是{1，2，…，m}，可表示为hi：{0，1}*→[1，m]，其中i∈[1，k]对于每个元素si∈S，把RBF中相应位置h1(si)，h2(si)，…，hk(si)都设置为1。

2.4.5 多棵Merkle哈希树

M-MHT 是一种认证的二叉树结构［35］，主要用来完成数据完整性验证，目的是有效且安全地证明一组元素是否被损坏和更改。M-MHT 顶部的节点称为根节点，根节点的身份验证提供了所有叶节点的完整性保证。M-MHT 根节点可以通过用户进行签名，并将其存储在服务器上，这也是它能保证数据安全性的主要原因。假设描述8 个叶节点的M-MHT，可设数据集S={s1，s2，…，s8}，h(i)=h(si)(i∈[1，8])。假设用户需验证数据块s3的完整性，则需要返回s3的哈希值h(s3)和相关辅助信息AI(s3)：{h1，2，h(s4)，h5，8}，通过验证根节点的真实性，所有块都被自动认证，以此方式来验证数据的完整性并确保存储的安全性。

3 本文方案

本章首先介绍一个高效和安全的数据结构来保证轻量级审计方案的实现，以及作为协议的基础建设；然后详细介绍了资源受限用户外包数据可验证审计方案。表1 给出了本文方案中使用的符号定义。

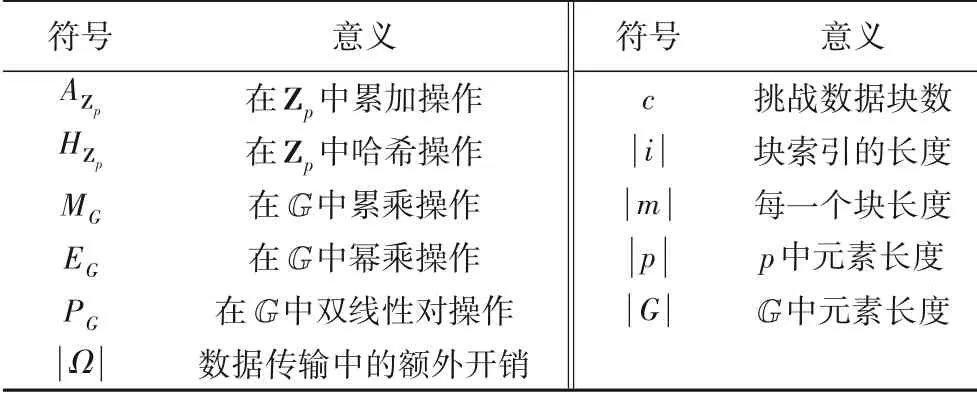
表1 本文方案中的符号定义Tab.1 Symbol definition for the proposed scheme

3.1 数据结构

为了让资源受限用户实现对外包数据的检索验证，其核心是需要提出一个数据结构来支持整个审计过程的完成；而且由于用户数据的实时更新，该数据结构还需支持数据动态功能。因此本文方案提出了一个高效和安全的新型数据结构，以满足用户对数据处理的实时需求。该数据结构主要是满足两方面的性能需求：首先该结构是高效的，检索速度快，计算开销小，可以使整个审计过程的时延很低，减少用户的经济损失；其次该结构是安全的，可以保证存储数据的安全性。

3.1.1 数据结构描述

标准的布隆过滤器只允许对元素进行插入和搜索查询操作，不支持元素的删除操作，一但存储到BF中，就不能删除数据记录。为了解决这一缺陷，Fan 等［36］提出了计数布隆滤波器（Counting Bloom Filter，CBF）。CBF 用计数器数组替换BF中的位数组，也就是说，每个比特位位置都是一个小计数器，它允许对CBF 执行插入、修改和删除操作。但采用传统CBF还不能满足数据结构的高效性，本文在CBF 结构基础上提出NCBF 结构，NCBF 除了支持数据动态操作，还可以与存储数据位置相关联，能极大提升数据动态处理和对数据查找验证的效率。设定一个由m个计数器组成的NCBF，用RNCBF表示，让U是一个大集合，其子集S={s1，s2，…，sn} ⊂U，随机选择k个相互独立的哈希函数H={h1，h2，…，hk}，对于每个元素si∈U，使用k个哈希函数将其映射到RNCBF的k个位置上，当元素插入或删除时，在对应的计数器上加1 或减1；修改操作采用先删除再插入的方式来实现。接着还需构造一个函数f：U→[1，M]，M∈Z，其中M是M-MHT 的总数量。该函数的目的是能快速访问数据存储在哪一棵M-MHT的数据结构中，且最坏函数f求值的时间复杂度为O(1)。为解决这个问题，采用了创建最小完美哈希函数的思想。将搜索函数f分为映射和查找两个阶段：首先将集合S映射到一个随机图G(V，E)上，其中V是一个顶点集，且，让两个相互独立的哈希函数满足(h1，h2)：U→V和另一个独立的哈希函数满足h3：U→ZMZ；E是图的边集，E={(h1(si)，h2(si))，si∈S，|E|=n=|S|}。接着查找G(V，E)中满足的哈希函数(h1，h2)，若查找到的(h1，h2)哈希函数使得G(V，E)是循环的，则重新更换两个新的且独立的，直到通过迭代查找到一个非循环图G(V，E)。这样得到的哈希函数就是完美的，它将访问次数减少到只有1 次，即实现时间复杂度为O(1)，并且节省空间。最后寻找一个函数g：V→ZMZ，使其对于每一个元素si∈S，让 等 式f(si) ≡g(h1(si))+g(h2(si))+h3(si)(modM)成立。该等式的计算结果f(si)指向数据元素si的存储位置。

相比哈希表、索引表等数据结构，NCBF 结构在存储空间和占用时间方面有较大优势，NCBF的数据存储和动态更新都能在O(1)内完成，这极大提高了数据查找验证的效率。但由于NCBF 并没有存储数据元素本身，因此还需要一个安全的结构来对数据进行存储，本文方案采用M-MHT结构来实现这一功能。M-MHT 是一个可以降低大型数据结构成本的二叉树结构，其中每个非叶子节点都为其子节点的哈希值。每一棵树的顶部有一个根节点，每个根节点都可以通过用户直接进行签名存储，使得结构本身可以确保数据存储的安全性。在本文方案中，令计算结果f(si)=Mj(Mj∈[1，M])，该结果指向数据对应的M-MHT 上，即可以跳过无关的M-MHT，直接跳转到所需信息的M-MHT上进行提取验证，这样可以大大减少数据在M-MHT上的搜索时间，因此该数据结构方案是高效可行的。

本文方案采用NCBF 来提高数据检索的效率。NCBF 结构数据插入和检索时间复杂度都为O(1)；而且可以将数据元素和存储位置相关联，跳过无关的存储位置信息，直接跳转到相关联的存储位置，显著减少搜索时延，从而实现高效存储和验证过程。但只满足高效性还不能达到整个审计过程的预期，因为NCBF 本身不是用来存储数据的，它主要是对数据存放位置进行指示，还需要一个结构来存放数据；其次它存在假阳性问题，可能会出现误判，把没有存储的数据信息返回为存储在结构中，该问题可能会引发敌手的攻击，通过欺骗用户来获取更多利益，会对审计过程造成安全隐患。因此为了数据存储和验证的安全性，本文方案引入了M-MHT，因为M-MHT结构的根节点可以通过用户来进行签名存储在代理上，当想要验证某条数据记录时，用户通过重新计算M-MHT根节点的签名来完成，这样可以确保数据的安全性。本文方案的数据结构是将NCBF 结构和M-MHT 结构进行结合得到，称为NCBF-M-MHT，如图2所示。

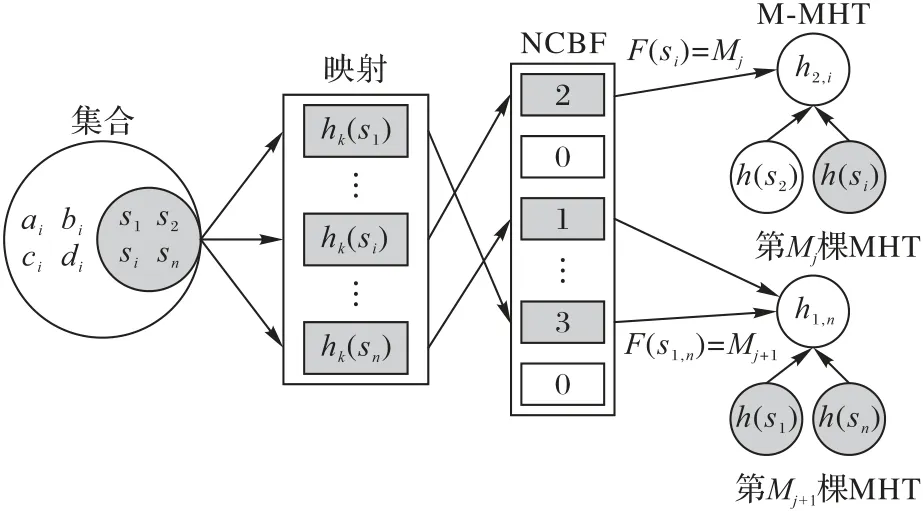
图2 NCBF-M-MHT数据结构示意图Fig.2 Schematic diagram of NCBF-M-MHT data structure

3.1.2 动态操作

本文方案的数据结构除了数据检索验证外，还支持用户数据的实时更新操作，主要包括用户数据的插入、修改和删除操作。

1）数据插入是将新的数据块插入到整个存储服务器的某些指定位置。假如用户想插入两个数据块I={x，y}，首先根据选取的k个哈希函数将数据块散列到NCBF 中，在NCBF 中对数据块信息进行更新，在相应位置增加1，接着对数据块标签信息进行存储，采用最小完美哈希函数的思想，将数据块与M-MHT 存储的位置相关联。对于数据块x，关联结果F(x)=Mj代表数据块的标签信息存储到第Mj棵MHT 上；同样，对于数据块y，关联结果F(y)=Mj+1代表数据块的标签信息存储到第Mj+1棵MHT 上，最后根据MHT 更新规则更新后生成一个新的根节点。插入结构如图3所示。

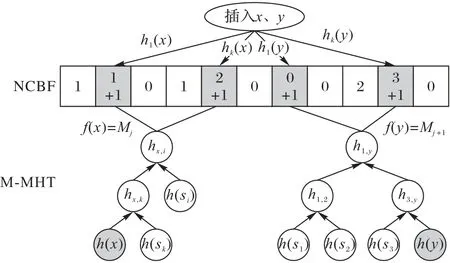
图3 数据插入示意图Fig.3 Schematic diagram of data insertion

2）数据删除是从存储服务器中移除数据信息，具体操作和插入操作相似，在NCBF 中是对相应位置减去1，通过关联后，在MHT中把标签信息删除，删除操作如图4所示。

3）修改操作是将已存储在服务器中的某些数据信息进行更正，具体操作和插入及删除一致，先对原有数据进行删除操作后，再把新的数据进行插入来完成。

3.2 设计协议

资源受限用户设备实现轻量级审计方案的协议由数据上传、审计验证和数据更新三个阶段构成，具体可由ParaSetup、RUDataBlind、HPSignGen、CSPStorage、ChalGen、ProofGen、ProofVerify、DataUpdate 这八个算法来进行描述。审计协议如图5所示。

1）ParaSetup：由PKG 来分发密钥。G1、G2和GT是p阶素数乘法循环群，p为素数乘法循环群的阶数，g是G1的生成元，双线性对为e：G1×G2→GT。全局参数GP={g，y，H，e，μ，pk}，其中H：{0，1}*→G1为哈希函数，y=ga，α∈Zp，μ是G1中随机产生的生成元，私钥sk={α，ssk}，(ssk，pk)为随机非对称加密密钥对。接着PKG 分别为RU 和HP生成私钥RUID和HPID。

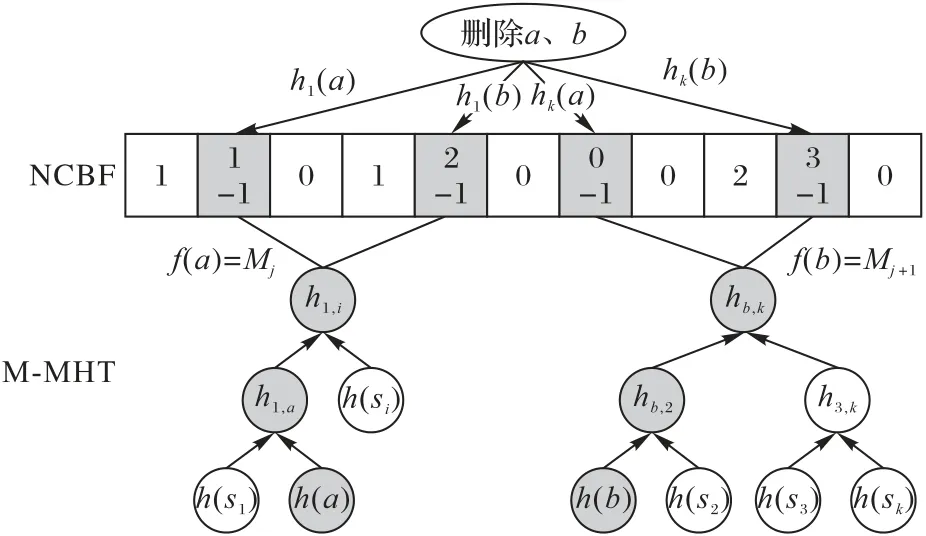
图4 数据删除示意图Fig.4 Schematic diagram of data deletion

a）数据块插入：若RU想在数据块mi之后插入数据块mi*，则由RU 将插入的数据块信息发送给HP，其中I代表操作类型为插入，i为插入数据块的位置。HP 在收到DI后计算它的数据签名，接着在数据结构中对NCBF 进行计数增加，并在MHT 中增加新的节点信息，最后把DI发送给CSP，CSP验证后在mi之后存储该数据块。

b）数据块修改：若RU 想将数据块mi修改为mi*，则首先发送修改的数据块信息DM={M，i，mi*} 给HP，其中M 代表操作类型为修改，i为修改数据块的位置。HP 在收到DM后重新计算它的数据签名，接着在数据结构中对NCBF 进行计数更新，并修改相应MHT 节点信息，最后把DM发送给CSP，CSP验证后将数据块mi进行修改并存储。

c）数据块删除：若RU 想删除数据块mi，则首先发送需要删除的数据块信息DD={D，i，mi} 给HP，其中D代表操作类型为删除，i为删除数据块的位置。接着HP 在数据结构中减少NCBF 的计数，并在MHT 中删除相关节点信息，最后把DD发送给CSP，CSP验证后将数据块mi删除。

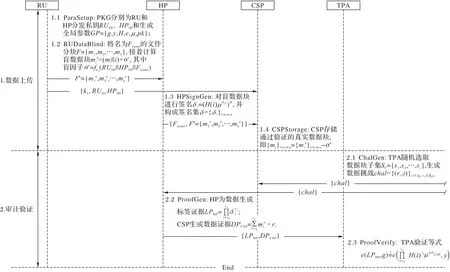
图5 审计协议示意图Fig.5 Schematic diagram of audit protocol

4 安全分析

本章利用博弈假设的方法，首先证明审计的可靠性和动态操作的有效性，然后用双线性对的知识来证明审计的正确性；接着考虑到CSP半诚信和TPA诚实好奇问题，在数据上传和审计过程中需要确保数据的隐私保护；最后针对本文方案的特殊场景存在的攻击方式进行安全分析。

定理1审计可靠性。审计挑战的数据块只有真正存储在CSP中，才能通过TPA验证，否则不能通过验证。

定理2动态操作有效性。在动态操作过程中，半诚实的CSP 必须按动态请求的要求来执行，不可能采用篡改或假装执行动态请求的方式来通过TPA的验证。

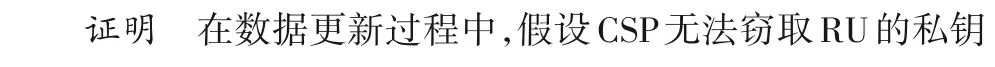
定理3审计正确性。只有CSP生成的数据证据和HP生成的标签证据同时有效才能通过TPA验证。

从式（6）可以看出，若LPHP或DPCSP无效，则不能通过上述等式验证。因此只有标签证据LPHP和数据证据DPCSP对应且同时有效，才能通过TPA验证。

5 性能评估

本章主要从理论和实验两个方面对方案的计算开销和通信开销进行分析。首先从理论方面分析了协议的计算开销和通信开销；接着通过搭建实验环境，模拟轻量级审计协议及构建动态数据结构过程来评估本文方案的开销；最后将本文方案使用的协议与其他方案进行对比，并对实验结果进行分析。

5.1 理论分析

5.1.1 计算开销

此外将本文方案与Tian 等提出的基于DHT 的审计方案（简记为DHT Audit）［25］、Shen等提出的基于LA-DLIT的审计方案（简记为LA-DLIT Audit）［27］和Wang 等提出的基于MHT 的审计方案（简记为MHT Audit）［19］在计算开销和通信开销两个方面进行了分析比较，结果如表3、4所示。

由表3可以看出，本文方案在RU端的数据计算阶段、CSP证明阶段和TPA验证阶段中与其他三个方案相比有显著的优势，因为本文方案通过引入HP 明显减少了RU 的计算量，并对审计各实体分配不同的操作流程，实现了针对RU 的轻量级审计。在数据上传生成签名阶段，本文方案比DHT Audit有显著改进，因为在验证过程中TPA无须生成验证证明，而是分配到HP和CSP进行；本文方案只需做两次配对就能完成验证，计算开销比LA-DLIT Audit和MHT Audit的低。

5.1.2 通信开销

通信开销主要针对的是验证阶段和数据动态更新两个过程，由于各数据结构不同，以及存储位置不同，导致它们的通信开销也不同，具体情况如表4 所示。与LA-DLIT Audit 和MHT Audit 相比，本文方案的通信成本有显著的优势。因为LA-DLIT Audit 和MHT Audit 将数据结构存储在CSP 端，这比起DHT Audit 将结构存储在TPA 上和本方案将结构存储在HP 上，需要更高的通信成本；与DHT Audit 相比，本文方案的优势并不明显，因为DHT Audit 的数据结构存储在TPA 上可以减少计算成本和通信开销。

表2 本文方案计算开销Tab.2 Computational cost of the proposed scheme

表3 不同方案计算开销对比Tab.3 Comparison of computational cost of different schemes

表4 不同方案通信开销对比Tab.4 Comparison of communication cost of different schemes

5.2 实验分析

本节通过实验来评估NCBF-M-MHT 审计的时间开销与动态更新操作时间开销，对上述的计算开销和通信开销进行验证，并将其与DHT-Audit、LA-DLIT 和MHT-Audit 进行比较。实验在配置为Intel Core i5-9300H CPU，8 GB 内存的笔记本电脑上进行，并搭建Linux 虚拟机，使用C 语言构建算法。实现的算法基于密码学库（Pairing-Based Cryptography，PBC），库版本为0.5.14 进行加密。采用MNT d159 椭圆曲线，它有一个160 位的组顺序，因此实验中p是一个160 位长度的素数，密钥参数长度设置为80 位，选用SH3-keccak256 作为安全哈希函数，共采用10 000 个数据块进行上传，400～5 000 个挑战数据块来验证数据完整性。

5.2.1 初始化阶段的时间开销

为实现数据的可验证性，用户在初始化阶段需要对上传数据进行一些相关操作后才能将数据发送到云端进行存储，并可将本地的数据副本删除。该过程共处理5 000个数据块，观察数据块从500增加到5 000间隔为500的性能曲线，如图6所示。与对比方案相比，本文方案中轻量级用户端RU 无须为数据块签名花费大量开销，只需对数据块进行简单的致盲处理，所以本文方案针对轻量级用户有明显优势。在数据块上传过程中，需要代理HP 为数据块生成签名，如图7所示，相比其他方案，DHT Audit 需要额外的n个哈希操作和配对操作，所需的开销最大，而本文方案与LA-DLIT Audit 和MHT Audit的开销无明显差异，而且本文方案少了一次哈希和幂操作，所以花费开销比LA-DLIT Audit和MHT Audit要低。

5.2.2 证明验证阶段时间开销

图8 显示了CSP 证明阶段的开销，CSP 在收到挑战请求后，为该挑战返回一个响应所需的时间成本。该过程总共处理3 000 个数据块，挑战的数据块数从600 增加到1 500，间隔为100，由于本文方案对各审计实体分配不同的操作流程，在CSP证明阶段只需完成c个累乘和累加的操作，所以时间开销较低，相较对比方案有明显的优势。图9 显示了TPA 验证阶段的时间开销，TPA 对返回的数据证明和标签证明进行验证所产生的时间成本。该过程共处理10 000 个数据块，挑战的数据块数从500 增加到5 000，间隔为500，该TPA 验证过程中，本文方案需要更少的幂运算、哈希和配对操作，因此相比其他方案有更低的计算开销。

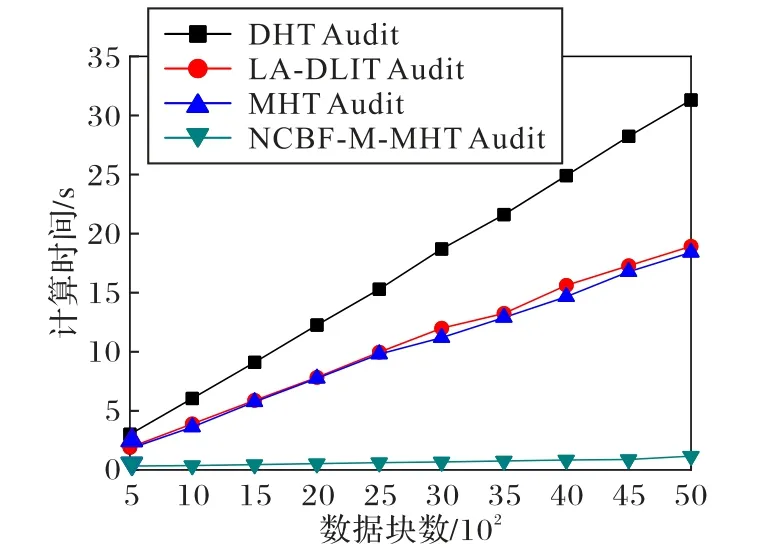
图6 RU时间开销Fig.6 Time cost of RU

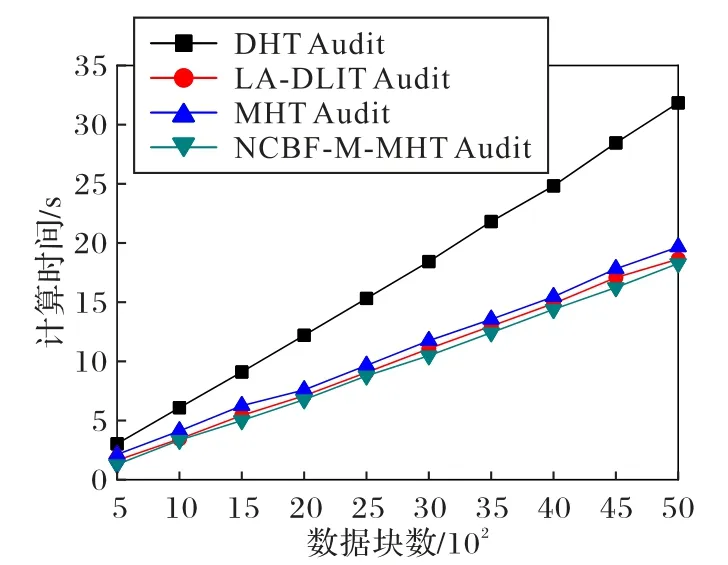
图7 数据上传开销Fig.7 Cost of data uploading

5.2.3 数据更新阶段计算开销

图10 展示了对数据更新的插入、修改和删除三个动态操作的时间开销，该过程处理更新数据块从20增至200，间隔为20。本文方案采用NCBF-M-MHT 数据结构，对数据块的插入和查找时间复杂度为O(1)；DHT Audit采用一个动态哈希表的数据结构，数据验证的复杂度为O(n)，需要花费的时间开销较大；LA-DLIT Audit 采用一个位置数组双向链接信息表构成数据结构，虽然可以减小时间开销，但无法抵御内部攻击；MHT Audit 采用一棵MHT 结构，对数据块的更新时间复杂度为O(logn)，但是随着数据块数增多，树的深度增加，查找花费时间开销较大。相比其他方案，本文采用的NCBF-M-MHT 数据结构性能更优，时间开销更低。

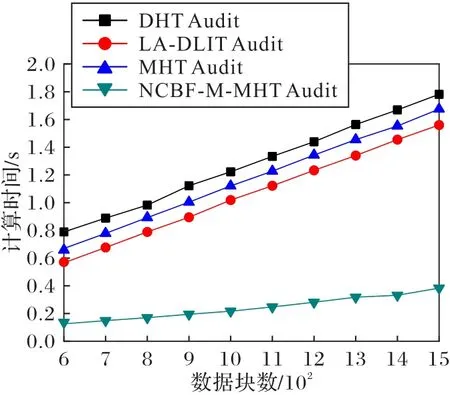
图8 CSP证明开销Fig.8 Cost of CSP certification

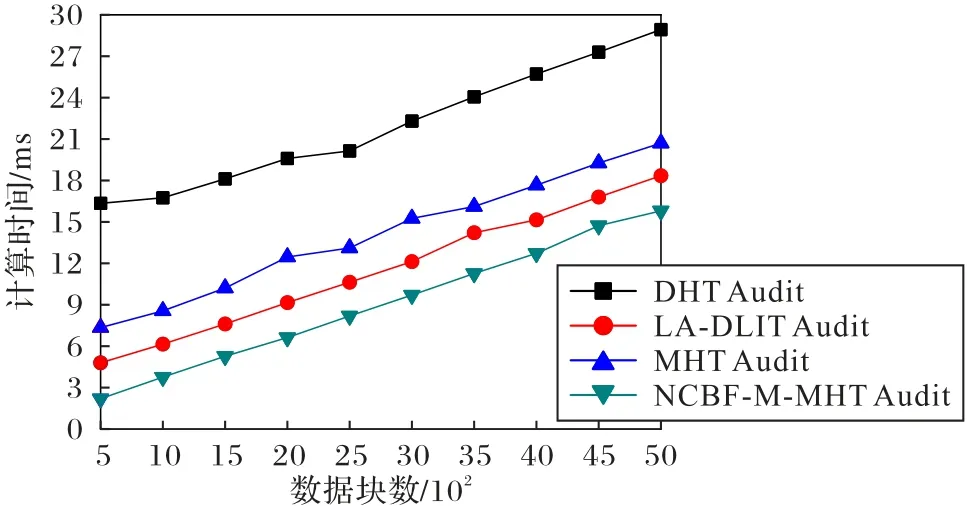
图9 TPA验证开销Fig.9 Cost of TPA validation

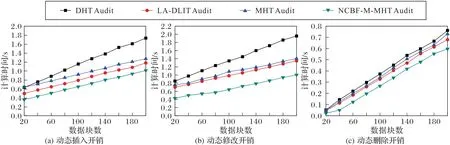
图10 动态更新开销Fig.10 Cost of dynamic updating

6 结语

本文提出了一个面向资源受限用户的轻量级审计方案。为了解决云数据完整性验证中存在的用户轻量级运算、数据隐私安全性和动态操作效率问题，首先引入诚信代理帮助用户进行复杂的签名操作，用户端只需对数据进行简单的致盲处理。其次为了满足动态需求，提出NCBF-M-MHT 数据结构来实现支持数据的插入、修改和删除操作。其中NCBF 可在O(1)时间内实现数据的插入和查找等操作；再结合M-MHT 对数据进行存储及通过用户对根节点签名来保证数据的安全性。接着为实现审计的正确性和完整性验证，通过对云服务器端返回的数据证据响应和代理端发送的标签证据来共同验证数据。性能分析与实验对比结果表明，本文方案是高效和安全的，且具有更低的时间开销。

总的来说，本文方案对于资源受限用户实现云数据完整性验证有一定的积极作用。但目前本文方案还只探讨了单个资源受限用户的数据完整性验证，如何高效且安全地实现多个轻量级用户间云数据共享审计验证将是下一步的研究方向。