“以学为中心”探讨一元函数∞-∞型极限求解方法
2021-03-06 09:13景慧丽李应岐
商丘职业技术学院学报 2021年1期
景慧丽,李应岐
(火箭军工程大学 基础部,陕西 西安 710025)

1 利用通分转化成型或型极限

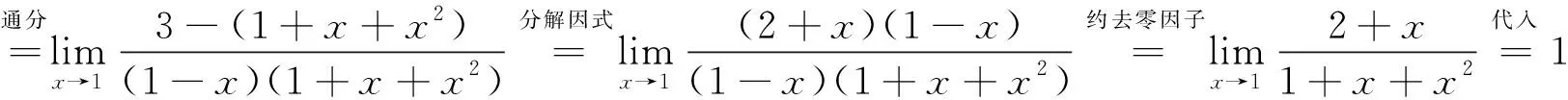



2 利用有理化转化成型或型极限
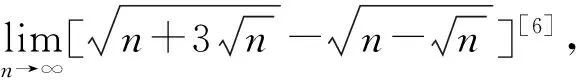

注3遇到用同次根式表示“∞”的∞-∞型极限时,首先考虑应用通分这种方法进行求解.如果遇到用非同次根式表示“∞”的∞-∞型极限时,就考虑用下述的方法3求解.
3 先提出变量的最高次幂,再应用倒代换转化成型或型极限
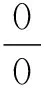

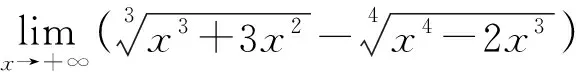


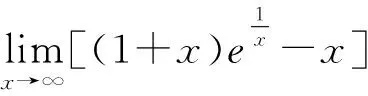

4 先利用倒代换,再利用通分转化成型或型极限

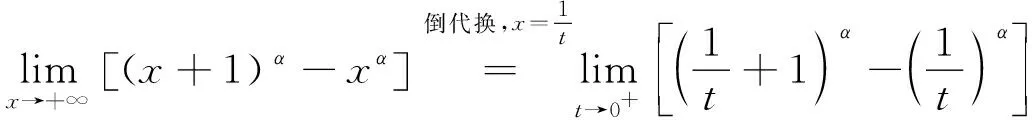
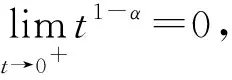
5 结语
以上就是求解一元函数∞-∞型极限常用的方法,每种方法都有自己的适用范围和使用条件.遇到∞-∞型的极限,首先应分析其特点,然后选择合适的方法进行求解.但是无论哪种方法,其求解思想都是“转化”,即数学中的“化归”的思想方法.数学中的“化归”就是把待解决或未解决的问题,通过转化的过程,归结到一类已经解决或者比较容易解决的问题中去,最终求获原问题之解答[9].其实,在高等数学课程中,蕴藏着很多“化归”思想和方法,在教学过程中,教员要善于挖掘高等数学课程中的“化归”思想,让学员领会并掌握“化归”思想和方法,进而培养学员的“化归”意识和能力,提高教学效率,激发学员学习数学的兴趣[10].
猜你喜欢
汽车实用技术(2022年5期)2022-04-02
中学生数理化·八年级数学人教版(2020年2期)2020-02-04
中学生数理化·八年级数学人教版(2019年2期)2019-12-31
制造技术与机床(2017年5期)2018-01-19
中学生数理化·八年级数学人教版(2017年2期)2017-03-25
中学生数理化·八年级数学人教版(2017年2期)2017-03-25
考试周刊(2016年88期)2016-11-24
考试周刊(2016年34期)2016-05-28
中国卫生标准管理(2015年24期)2016-01-14
中国塑料(2015年5期)2015-10-14

