基于SW Simulation的电动方程式赛车车架轻量化设计与优化
吉文哲,李 浩,朱 凯
(商丘职业技术学院,河南 商丘 476100)
通过轻量化设计,减轻整车重量、增加续航里程,是新能源汽车技术发展的一个重要研究方向.车架是电动方程式赛车的基体,其重量约占整车整备质量的15%~20%.在保证安全的前提下,减轻车架的自重有助于实现整车的轻量化,从而提升电动赛车的续航里程[1].为了参加人力资源和社会保障部、中国机械工业联合会共同主办的首届全国新能源汽车关键技术技能大赛——汽车装调工(新能源汽车轻量化技术)赛项,我校自主设计并制作了一辆纯电动方程式赛车.本文以该赛车的车架为研究对象,通过有限元分析法,对车架上具有富余强度的结构进行优化改进,再经过多种典型工况下刚度和强度的校核,保证车架满足安全性、可靠性的要求,从而最终实现车架的轻量化.
1 电动赛车车架初始设计
1.1 车架的结构设计
通过调研和文献资料的查阅得知,桁架式车架往往比承载式车架的强度与刚度更高,且容易加工制作,因此参赛车架最终选用了空间桁架式的结构[2].结合大赛规则要求,并充分考虑人机工程学,在Solid Works软件中对车架进行了分段造型设计,主要包括驾驶舱、主环、前舱、前环及后悬安装区等结构的设计,最终建立了鲨鱼流线型的车架三维模型,总尺寸为2283 mm×1167 mm×1495 mm(长×宽×高),如图1所示.

图1 鲨鱼流线型车架模型
1.2 车架的材料选择
本次电动方程式赛车车架所有的杆件均采用30CrMo钢管,即4130钢管,其物理性能如表1所示.4130钢管强度高、延展性好,在保证车手安全的前提下,钢管的壁厚相对薄一些,有助于车架的轻量化设计.本次车架使用了不同外径和壁厚的钢管,如车架主防滚架,使用了25 mm×1.6 mm(外径×壁厚)的管材;斜支撑等辅助构件,采用20 mm×1.2 mm(外径×壁厚)的管材.不同直径、不同壁厚钢管的搭配使用,减轻了车架的总体重量.

表1 4130钢的物理性能
2 初始车架有限元分析模型的建立
2.1 车架壳单元模型构建
本次电动方程式赛车的车架全部由规则的圆形钢管组成,其截面形状相同,所以,在有限元分析时采用壳单元建模,可提高分析时的计算精度.Solid Works软件自带的Simulation插件可直接在车架三维模型的基础上进行有限元建模,不用进行中间格式的转换,方便快捷.
使用Solid Works软件的中面命令直接抽取车架杆件的中面,然后再切换到Simulation插件中,赋予杆件不同的直径、壁厚和材料属性,即可建立车架的壳单元模型.这样建立的有限元模型,既能反映出车架的实际结构,又能在保证计算精度的基础上减少运算量.
2.2 模型网格划分
网格划分精细程度的好坏对分析结果的精度和正确性有重要影响.本文所研究的车架结构形状比较规则,尺寸规模适中,可采用较小的单元尺寸划分网格,软件中设置单元尺寸为60 mm,公差3 mm,共划分25 701个单元,共计31 215个节点.最终的车架有限元网格模型,如图2所示.
图2 车架网格划分模型
3 初始车架强度分析与优化
3.1 弯曲工况分析
弯曲工况分析是指满载的赛车在静止或良好的路面上匀速直线行驶时,车架的受力和变形情况.分析时,忽略车轮和前后悬架的质量.车架主要承受车手、动力电池组、驱动电机、车架自重等静载荷,其中,车手重量规定要达100 kg,不足的在驾驶舱放置沙袋,所以,弯曲工况的载荷情况,如表2所示.由于行驶中存在动态效应,故车架承受的静载荷需乘上动载因数,其一般为2.0~2.5[3].为提高赛车的安全系数,本次分析中动载因数取2.5.

表2 满载弯曲工况载荷 kg
将表2中载荷等效加载到车架承载处后,选取与车辆坐标系相同的方向设置约束,主要约束左前、右前悬架铰接点Z方向的自由度以及左后、右后悬架铰接点X方向、Y方向和Z方向的自由度,释放其他自由度.约束点位置,如图3所示.运行软件进行分析计算,可得到该工况下的应力分布和变形情况,如图4、图5所示.
由图4可知,应力集中的部分几乎都发生在杆件的连接处,比较符合力学分析的结果.该工况下最大应力为96.59 MPa,出现在右侧防滚架多个管件的连接处,但远小于4130钢管的屈服极限785 MPa,有很大的富余量.从图5可知,弯曲工况下车架的最大位移2.415 mm,出现在右侧座椅与驾驶舱底部横梁的连接处,变形量比较小.
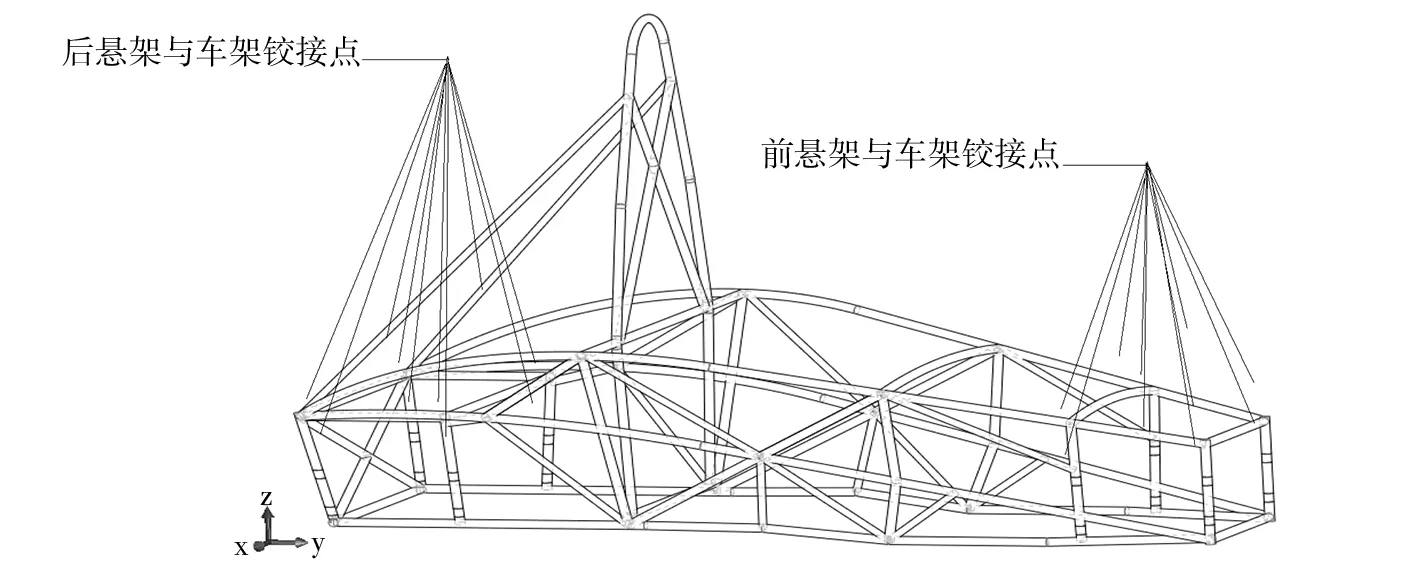
图3 车架自由度约束位置及方向
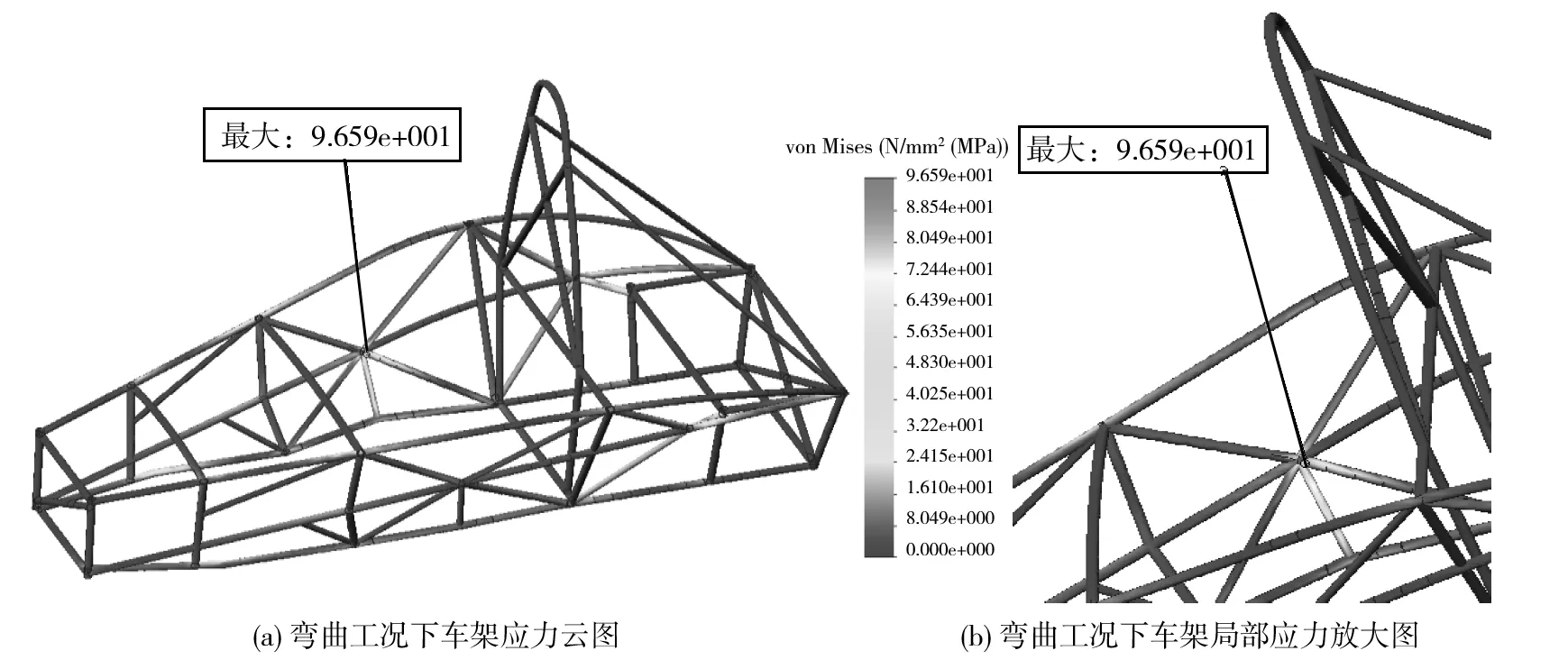
图4 初始车架弯曲工况下应力分布图
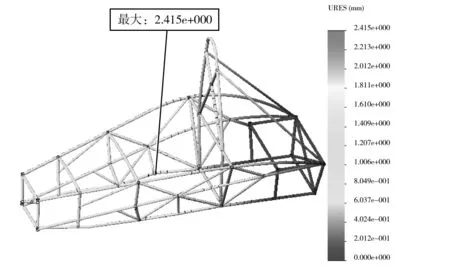
图5 初始车架弯曲工况下变形云图
3.2 扭转工况分析
车架安全性能测试环节要求在左前轮(或右前轮)和右后轮(或左后轮)同时抬起时能承载200 Kg重物的重压,这比较考验车架的扭转刚度.该工况在有限元分析时,约束点与弯曲工况相同.在约束右前、左后悬架与车架铰接点Z方向的自由度以及左前、右后悬架与车架铰接点X方向和Y方向的自由度同时,分别给车架左前悬架安装点和右后悬架安装点方向相反的1 mm的规定位移.经计算可得到车架此种工况下的应力和位移分布,如图6和图7所示.

图6 初始车架扭转工况下应力分布图

图7 初始车架扭转工况下位移分布图
由图6可知,在这种比较恶劣的工况下,车架的最大应力达216.3 MPa,出现在右前悬架支柱和防滚架的连接处,但仍小于材料的屈服极限.车架前后端交叉管件的焊接处应力较大,在焊接时需注意这些地方焊接精度的控制.由图7可知,扭转工况下最大位移出现在主环的顶部,值为1.222 mm,变形幅度不是很大.
3.3 初始车架结构优化改进
经上述分析可知,车架初始设计时比较保守,刚度的富余量较大,特别是包含杆件数量较多的前环,刚度余量最明显,优化改进空间较大,可通过以下几个方面进行轻量化改进:
1)因弯曲和扭转工况下前环杆件处的应力和变形都比较小,故可以将前环较多的杆件省去,只保留仪表杆与前后斜支撑杆件,将它们共同焊接在车架上,保证前舱的刚度和强度.
2)改变防火墙后部与动力电池安装支架相连接的两根斜支撑钢管的直径和壁厚,由25 mm×1.6 mm(外径×壁厚)的钢管改成20 mm×1.2 mm(外径×壁厚)的钢管.
3)弯曲工况下,最大应力出现在右侧防滚架多根杆件的连接处,需保证此处良好的焊缝来承受较大的应力,因此,也将此处及与此处位置对称的四根25 mm×1.6 mm(外径×壁厚)的钢管改成20 mm×1.2 mm(外径×壁厚)的钢管,保证斜支撑杆件的规格一致.
优化后车架的结构,如图8所示.车架的质量降为34.16 kg,与优化前相比,减重3.63 kg,具体的轻量化明细,如表3所示.
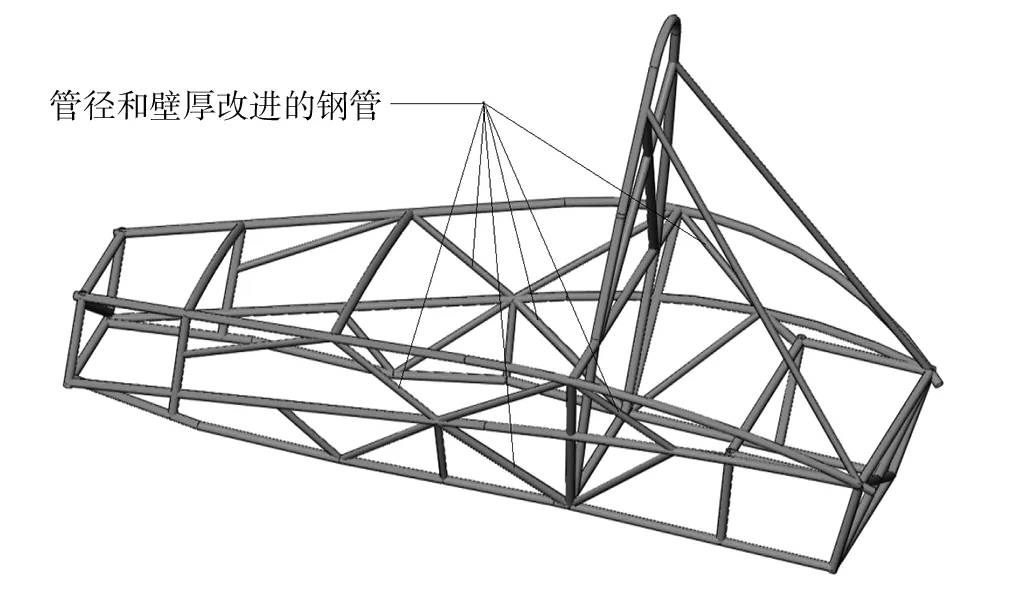
图8 优化后车架的结构

表3 车架结构优化前后质量对比
4 优化后车架强度校核
4.1 优化前后车架的分析结果对比
将优化后的车架再次导入Simulation中,分析其弯曲工况和扭转工况下的静力学性能.为突出与优化前车架的对比效果,设置与初始车架分析时相同的加载和约束,运算后得到的应力和位移分布情况,如图9至图12所示.
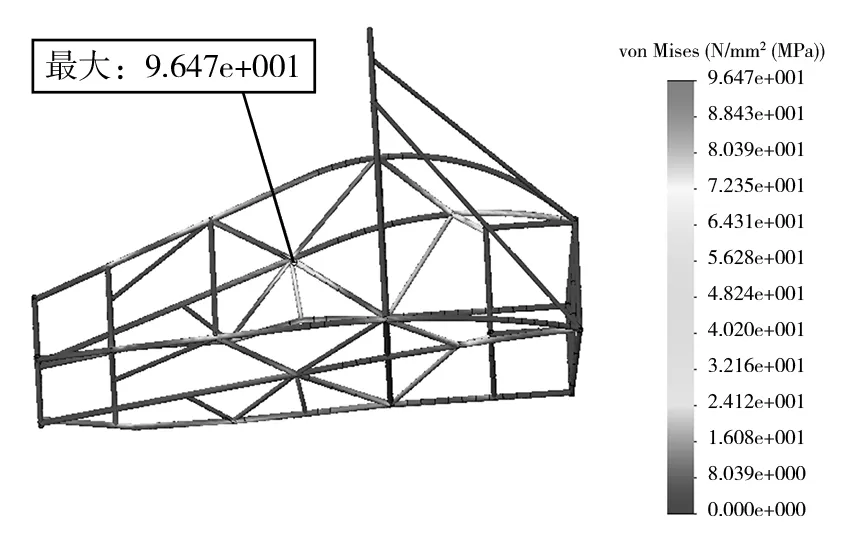
图9 优化后车架弯曲工况应力分布图
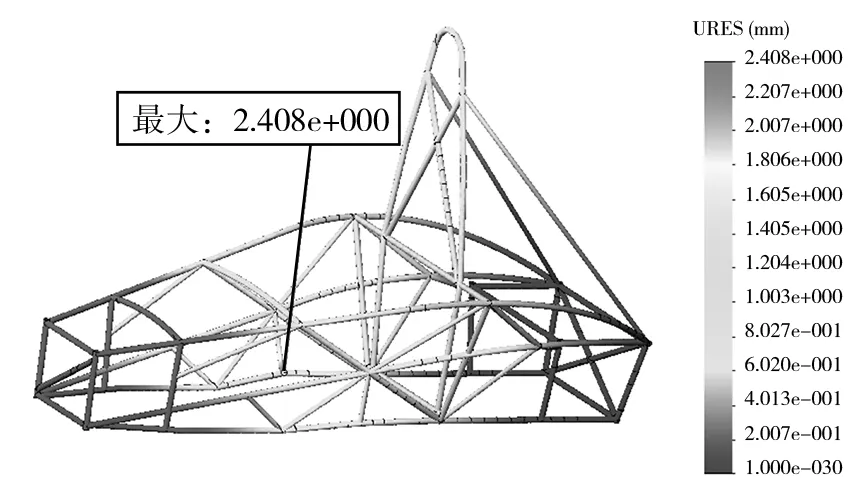
图10 优化后车架弯曲工况位移分布图
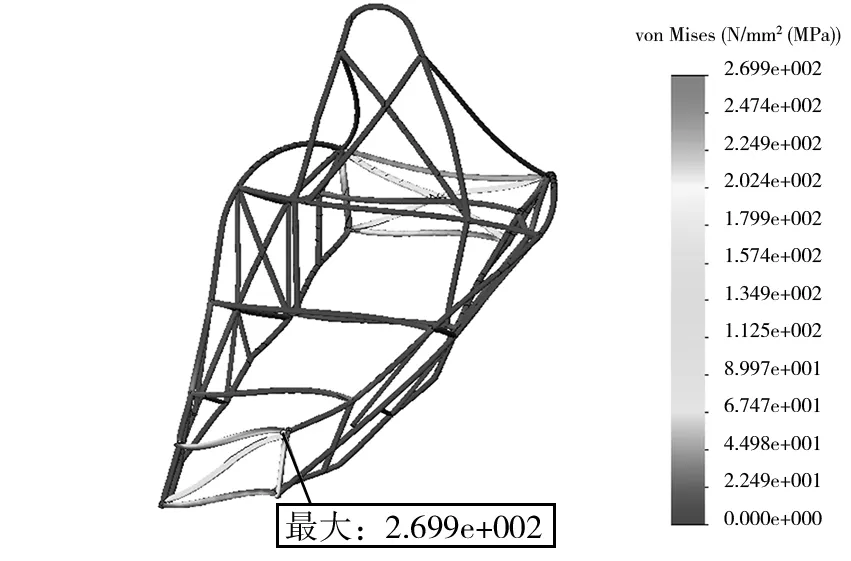
图11 优化后车架扭转工况应力分布图
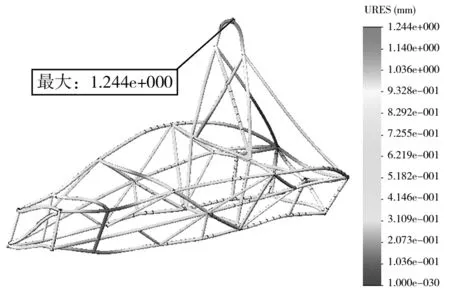
图12 优化后车架扭转工况位移分布图
从优化后车架的应力和位移云图中可看出,弯曲工况下最大应力为96.47 MPa,最大位移为2.408 mm,与优化前的最大应力96.59 MPa和最大位移2.415 mm相比,出现的位置相同,数量上变化不大,且均远小于材料的屈服极限.
同理,从扭转工况的应力和位移云图中可知,车架的最大应力为269.9 MPa,最大位移为1.244 mm,与优化前最大应力216.3 MPa和最大位移1.222 mm相比,最大位移几乎没有变化,最大应力虽然有所增加,但远小于材料的屈服极限.
4.2 紧急制动工况分析
赛车在紧急制动时,除车身及承载部件的重力作用在车架上外,较大的地面制动力也通过车轮和悬架系统作用到车架上.为保证赛事的安全,本次竞赛赛车的最大设计速度为40 km/h,制动距离5 m,由此可计算出制动加速度为12.3 m/s2,赛车车架与电机、电池、悬架及轮胎等承载部件的总质量为130 kg,车手质量为100 kg.因此,紧急制动时加载的总质量为230 kg,动载因数取1.5,则整车制动力为:
F=230×12.3×1.5 =4243.5 N
在做有限元分析时,将该制动力平均分布在悬架和车架的20个连接点处,每个连接点的纵向制动力为212.2 N.约束位置与前面工况相同(约束前悬架与车架铰接点X、Y、Z三个方向的自由度以及后悬架与车架铰接点X、Z两个方向的自由度),释放其他所有的转动自由度.运算后可得车架紧急制动工况下应力和位移分布,如图13和图14所示.车架最大应力为86.86 MPa,远小于材料的屈服强度. 最大应力出现在车架后舱动力电池和驱动系统安装区上部,这主要是由于整车的主要质量都集中在该区域,紧急制动时会产生较大的惯性. 车架最大变形量为0.6799 mm,出现在前环与右侧主防滚架连接点附近,但由于设计车速不高,变形量也较小,说明在此工况下,优化后的车架是能够充分满足强度要求的.
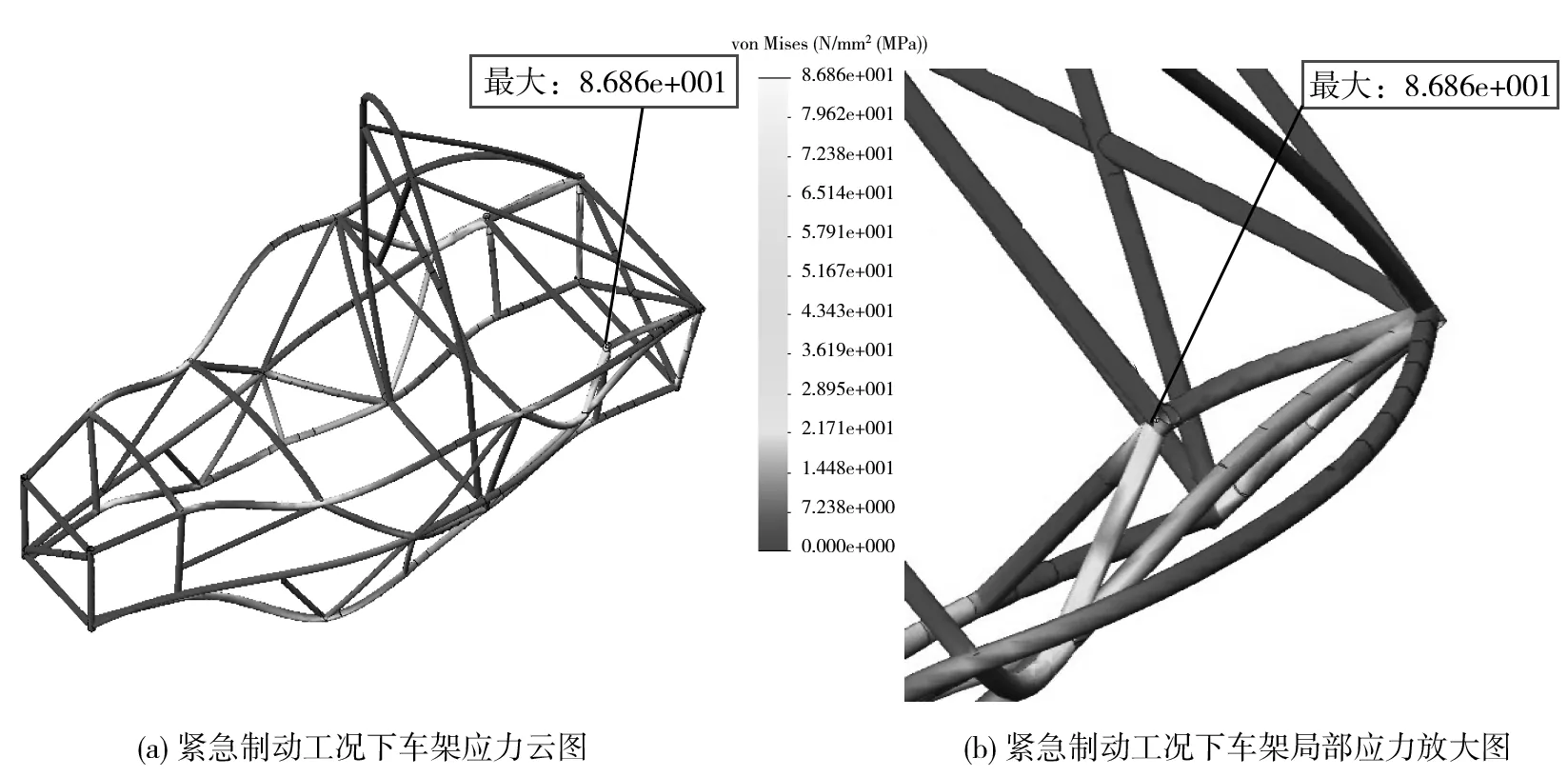
图13 优化后车架紧急制动工况应力分布图
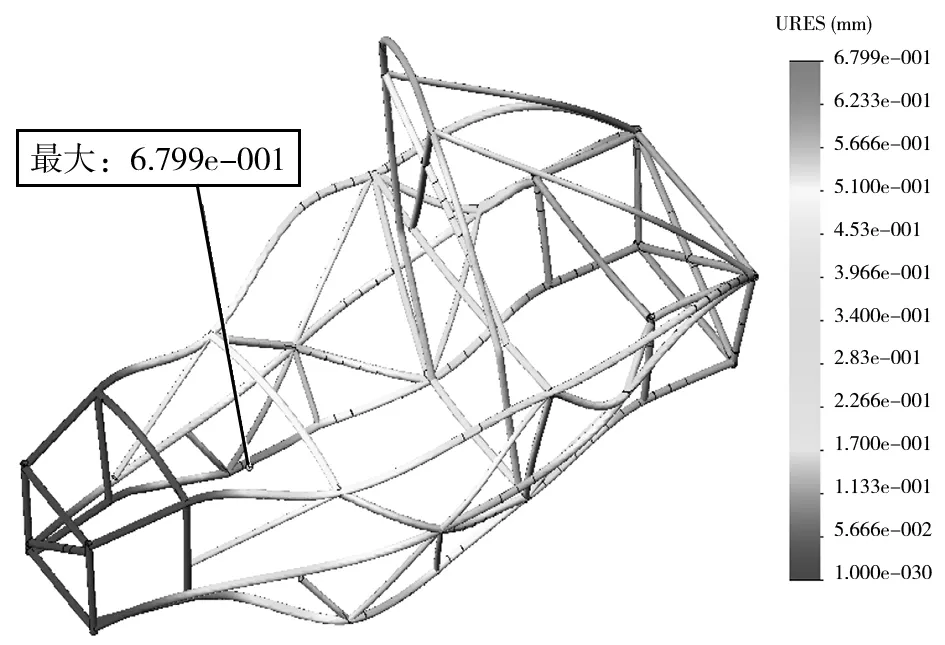
图14 优化后车架紧急制动工况位移分布图
4.3 转弯工况分析
赛车在赛道上转弯行驶时,由于离心力的作用,车架会受到侧向载荷,所以,车架要有一定的侧倾刚度.同时,在转弯行驶时,必然会伴随着赛车的制动过程,所以车架还会受到纵向制动力.赛车转弯时的向心加速度与赛车的车速和转弯半径息息相关,因此,在分析转弯工况时参考国内外其他类型赛车的处理经验进行近似计算.本文取赛车受到侧向加速度0.9 g和纵向加速度0.5 g来模拟左转弯,动载因数取1.5[4].则车架受到的侧向力为:
F侧=230×0.9×9.8×1.5=3042.9 N
车架受到的纵向制动力为:
F纵=230×0.5×9.8×1.5=1690.5 N
与制动力类似,侧向力同样通过悬架系统传递给车架,故将车架受到的侧向力和纵向制动力平均等效作用到前后悬架和车架的连接点处.约束位置同前面工况(约束左前悬架铰接点X方向与右前悬架铰接点Y方向和Z方向的自由度以及左后悬架铰接点Z方向与右后悬架铰接点X、Y、Z三个方向的自由度),释放其他自由度.分析结果,如图15和图16所示.经分析可知,左转弯工况与紧急制动工况类似,最大应力为88.42 MPa,出现在车架后舱动力电池和驱动系统安装区上部,远小于材料的屈服强度;在前环与右侧主防滚架连接点附近的最大变形量为0.7639 mm,变形不大.故可认为,在转弯工况下,优化后的车架满足强度的要求.

图15 优化后车架转弯工况应力分布图
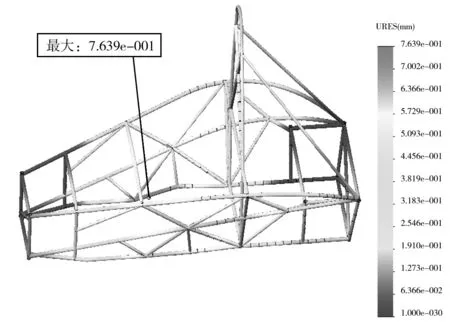
图16 优化后车架转弯工况位移分布图
4.4 模态分析
模态分析可计算车架的固有频率、阻尼比和模态振型等,其中,固有频率直接影响赛车的舒适性、噪音控制、疲劳寿命及驾驶员的人身安全等.为防止发生共振,车架的固有频率应避开赛车运行环境中激励源的频率.
本次只进行车架自由模态分析.车架的自由模态跟外部加载载荷无关,只取决于自身的结构和材料,因此,分析时不需要添加任何约束和载荷[5].分析结果,如图17所示.
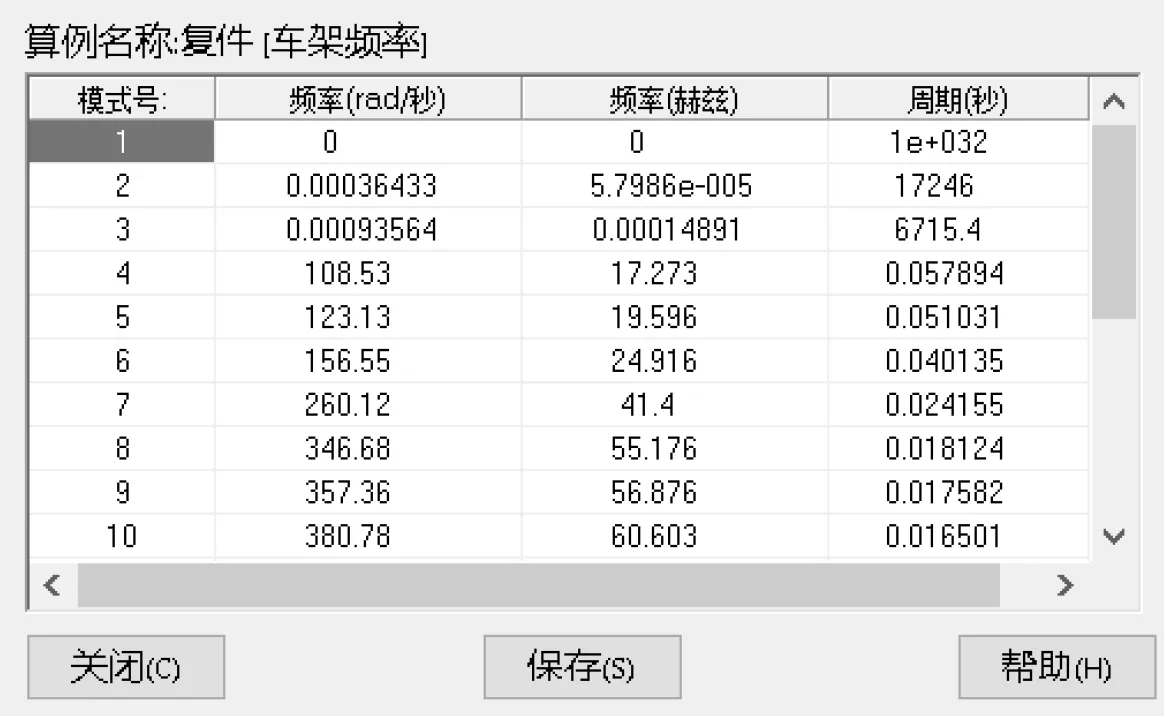
图17 车架自由模态分析结果
由于分析的是车架在自由状态下的模态,前三阶模态近似于0 Hz,没有参考意义,因此,选取第四阶模态作为实际的起始模态,车架的前六阶模态振形,如图18所示.
在模态分析时,车架的外部激励源一般主要考虑路面激励、车轮不平衡引起的激励和发动机激励三个激励源.因本次研究的为电动赛车,故不考虑发动机激励的影响.赛道的激励可参考城市路面,激励频率一般在5 Hz以下,因此,车架的低阶模态应尽量高于5 Hz[6].车轮不平衡引起的激励频率一般在11 Hz以下,且所占比例较小,通过技术手段也可尽量减小.
通过分析得知,车架的前六阶模态频率分布在17.273 Hz~56.876 Hz之间,车架的固有频率很好的超过了路面激励和车轮不平衡激励的频率,因此,优化后车架的固有频率完全满足设计要求.
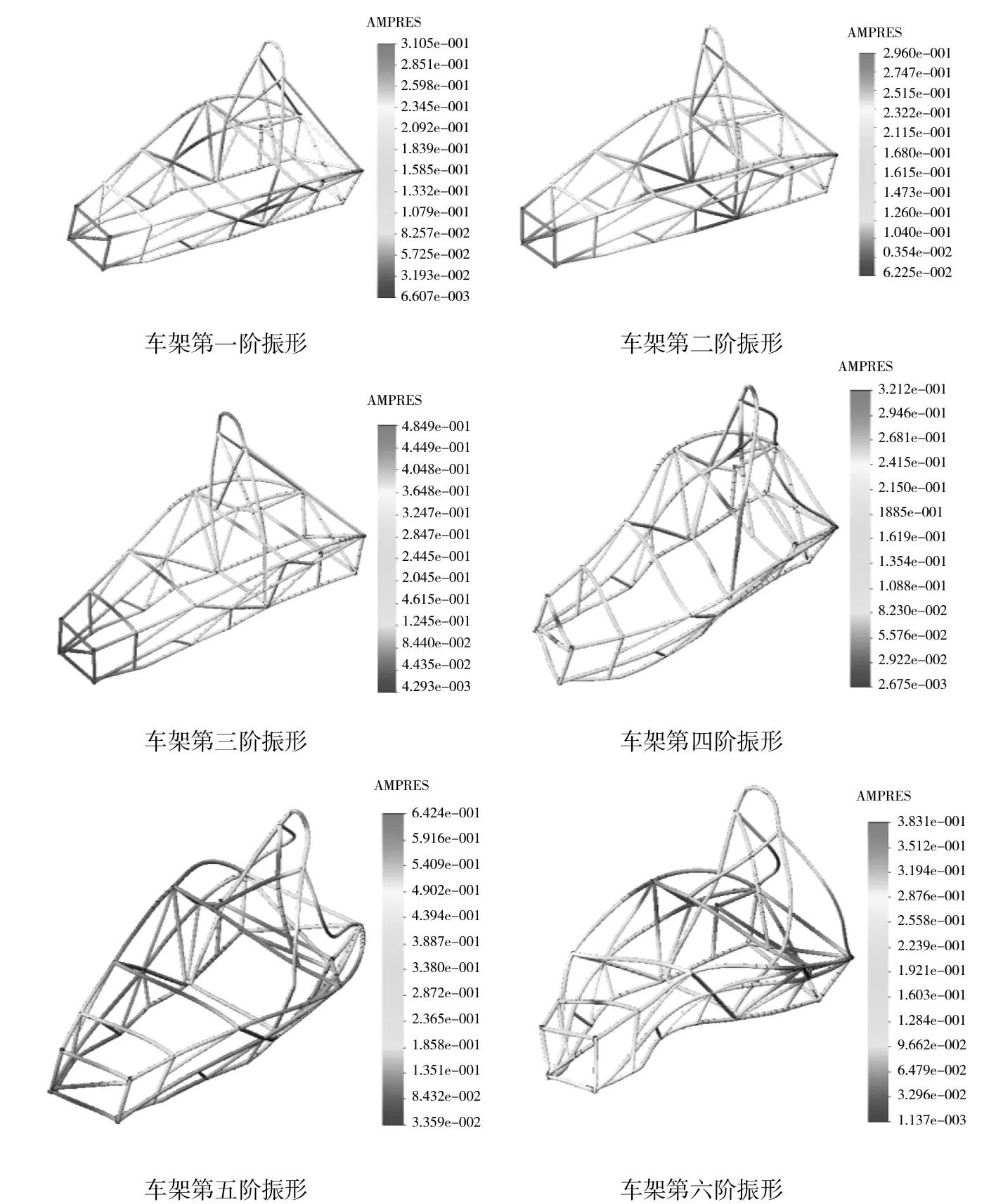
图18 车架前六阶阶振形
5 结语
本文基于人机工程学,在Solid Works中建立了电动方程式赛车车架的三维模型,又在 Simulation中以壳单元的形式建立了车架的有限元分析模型.通过合理的加载与约束,得到弯曲和扭转两种工况下有限元分析的结果,并据此对车架原始结构进行了优化,使车架减重比达9.6%.对优化后的车架不仅进行了与初始车架同等条件下的弯曲和扭转工况分析,还增加了紧急制动、转弯工况和自由模态的有限元分析.分析结果表明,优化后的车架既减轻了自重,又符合材料强度的要求,而且有效避开了赛车运行过程中的激励频率,不会产生共振现象.同时,这种简化分析模型方法为类似车架的结构优化设计提供了参考.

