约束非线性最优化迭代方法解析γ能谱重峰
陈 晔 肖无云 李京伦 张羽中 赵 辉 法 锋
1(国民核生化灾害防护国家重点实验室北京102205)
2(陆军装备部北京100072)
γ能谱测量分析可以实现快速、可靠的放射性核素定性识别和定量分析,在核辐射监测、辐射防护、核物理研究等方面应用广泛[1]。由于γ谱仪系统受探测器本征能量分辨率的限制,当存在能量接近的射线时,能谱中会产生重峰,不利于射线能量和强度计算。因此复杂谱处理通常需要进行重峰解析。
当前,虽然已经有基于直接解调、压缩感知、凸优化等理论的全谱反演方法用于γ能谱解析[2-6],但是该类方法需要对系统响应函数进行精细刻度,刻度过程中的误差会影响测量分析结果;此外,全谱反演方法往往需要更大的工作量和运算量,而在很多应用场景中,可能只关注能谱的局部区域,全谱分析是不必要的[7]。
重峰解析的目的在于从能谱数据中确定各个峰的峰位和峰面积(分别对应射线的能量和强度)等参数。非线性拟合是一种应用广泛的数据分析和参数估计方法,它利用优化算法最小化拟合函数与能谱之间的均方误差(或加权均方误差),实现对峰参数的估计,是一种经典的γ能谱重峰解析手段[8]。拟合函数通常由峰形函数和本底函数两部分组成。例如,对NaI(Tl)和LaBr3(Ce)等常用闪烁谱仪测量的γ能谱,其全能峰可用高斯函数描述,而本底可用线性或者二次函数的形式[7,9-10]。通常本底函数可以利用峰区两端的数据确定[7,11],或采用统计敏感的非线性迭代剥峰(Statistics-sensitive Nonlinear Iterative Peak-clipping,SNIP)[12-13]等本底估计方法获得[14-15]。因此可提前将本底扣除,后续的非线性拟合只关注高斯峰的解析[16]。在优化算法上,常用方法包括Levenberg-Marquardt(LM)算 法[14,16-18]、信 赖 域(Trust Region)算 法[11,19]和Nelder-Mead单 纯 形法[15]等。
通常情况下,非线性最小二乘可以得到较准确的拟合结果。然而,重峰解析问题的复杂度高,受统计涨落、重峰个数、峰间距等多种因素影响,在统计涨落水平较高(如测量时间短、计数少等)或待测辐射场较复杂的应用场景中,传统拟合方法的解析精度相对较低。研究表明:充分利用已知的先验知识,为拟合问题增加约束或减少待定参数的个数,有利于提高拟合的准确度[20-21]。为解决传统方法存在的上述问题,本文提出一种改进的重峰解析方法,利用峰宽刻度信息对非线性最小二乘问题增加约束,并采用迭代求解法,实时更新峰宽和权重等信息,保证解析结果收敛到更准确的位置,提高重峰解析精度。
1 方法原理
1.1 约束非线性最优化解析重峰
设扣除本底后的待解析能谱中第i道的计数为Si,i1≤i≤iN,i1和iN为峰区的起始和结束道址,N为峰区内数据点数。采用的峰区拟合函数为高斯峰叠加的形式,如式(1)所示:

式中:Gaj,uj,σj(i)为高斯函数;aj、uj和σj分别为高斯函数的高度、中心位置和标准差,如式(2)所示;M为全能峰的个数;j为全能峰的序号,1≤j≤M;θ为待定参数向量,如式(3)所示,共有3M个待定参数。

拟合的目的是求得待定参数θ的值,从而获得各个峰的参数。在传统非线性最小二乘方法中,拟合问题转化为最小化加权均方误差的形式[8,10],如式(4)所示。

其中:wi为权重系数,根据能谱计数泊松分布的统计特性,权重系数设置为:

在解析高复杂度、高统计涨落的重峰时,上述传统方法的误差较大。针对该问题,本文使用γ谱仪的峰宽刻度信息对拟合问题进行约束。γ能谱全能峰的半高宽(Full Width at Half Maximum,FWHM)可以表示为能量或者道址的函数,该函数通过实测谱刻度得到[22]。设FWHM与道址i的关系为函数F(i),据此可将式(4)中待求解的问题变为一个带约束的非线性最小二乘优化问题,如式(6)所示:
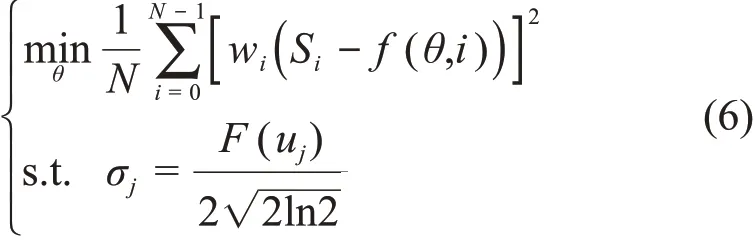
1.2 迭代求解方法
为了求解式(6)中带约束的非线性优化问题,提出了一种简单的迭代方法,具体步骤如下。
第1步:设置待定参数的初值θ(0):
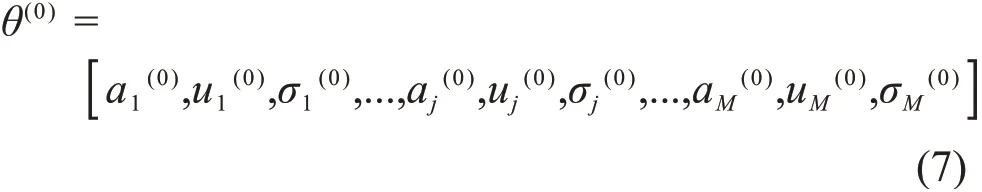
第2步:设置待定参数取值范围的上下界θL、θU:

其 中:aL,j=1,aU,j=2max(Si),uL,j=i1,uU,j=iN,的上下界都与初值相同,,即每次迭代中,将σj作为常数);
第3步:开始迭代拟合,设n为迭代的次数;
第4步:在第n次迭代中,利用权重系数wi、参数初值θ(0)和参数取值范围θL、θU,使用LM或信赖域等最优化方法对重峰数据进行非线性最小二乘拟合,得到第n次迭代的结果,设为θ(n):
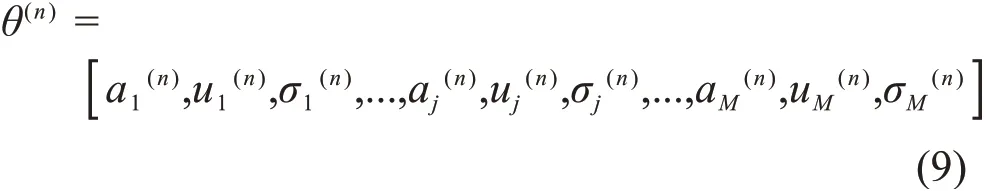
第5步:判断是否满足迭代终止条件:如果连续两次迭代拟合结果之间的欧式距离大于阈值ε,即|θ(n)-θ(n-1)|>ε,则不满足终止条件,执行第6步;如果|θ(n)-θ(n-1)|≤ε,则满足迭代终止条件,结束迭代,最终确定的参数为θ(n),执行第7步;
第6步:更新参数并进入下一次迭代:首先根据第n次迭代的拟合结果θ(n)以及峰半高宽刻度F(i),更新待定参数初值、权重系数和σj的取值范围,然后令n=n+1,返回第4步,继续进行下一次迭代;
第7步:根据拟合结果计算各个全能峰的峰位、峰半高宽和峰面积信息,完成重峰的解析:设pj、FWHMj和Aj分别为第j个全能峰的峰位、峰半高宽和峰面积,则有
2 仿真验证
首先使用仿真数据验证方法的性能。使用MATLAB软件,在400~600道范围内,根据峰位、峰面积和FWHM参数仿真产生两个叠加的高斯峰,然后添加泊松噪声,得到仿真γ能谱重峰数据。
能谱计数的统计涨落水平、峰之间的距离以及峰之间的面积比等参数不同,重峰解析的难度也不同。因此在生成仿真数据时,调整上述参数,研究其对方法性能的影响。由于能谱计数服从泊松分布,总计数越大,统计性越好。因此可通过调整全能峰面积模拟统计涨落的影响。
每种条件下生成2 000组重峰数据,解析得到峰位、FWHM以及峰面积信息,统计其平均误差,并与传统方法的结果对比。为求解式(4)和式(6)中的最优化问题,采用了MATLAB中的fit函数,其底层使用的最优化方法为信赖域算法。
图1 展示了三组典型的仿真重峰数据及其解析结果。虽然两种方法得到的拟合曲线都与模拟谱符合,但是重峰解析结果却存在较大差别。可见,拟合曲线与谱数据的符合程度并不能准确反映重峰解析的质量,应该使用峰位、峰面积、FWHM等峰参数的误差判断解析结果的优劣。
2.1 统计涨落的影响
固定两个高斯峰的峰位分别为480道和520道,两者的峰面积相同,并由100逐步增加到10 000。解析得到的峰位、FWHM和峰面积的平均误差随峰面积的变化情况分别如图2(a)、图2(b)和图2(c)所示。可以看出,随着峰面积的增大,由于能谱计数的统计涨落减少,两种方法的误差都呈下降趋势,该结果与理论预期一致。同时,本方法解析结果的误差一直低于传统方法。特别是在峰面积较小,即数据的统计涨落较高时,本方法可以有效提高解析精度,在峰面积为100时,峰位误差降低了27%,峰面积相对误差降低了71%,说明其抗统计涨落能力强。
图2 (d)为两种方法解析结果对应的目标函数取值情况。可见,传统方法的拟合曲线与模拟谱的残差比本方法低;然而,图2(a)至图2(c)的结果已经证明本方法解析的峰参数精度更高,这说明拟合残差小并不代表实际解析效果好,传统方法存在过拟合问题。本方法利用了峰宽刻度信息为最优化问题增加了约束,虽然拟合残差比传统方法高,但是能够得到更符合实际物理规律的结果,从而提升解析精度。在峰间距影响的研究结果图3(d)中也得到了类似的结果,这些结果符合理论预期,验证了为优化问题增加约束的效果。
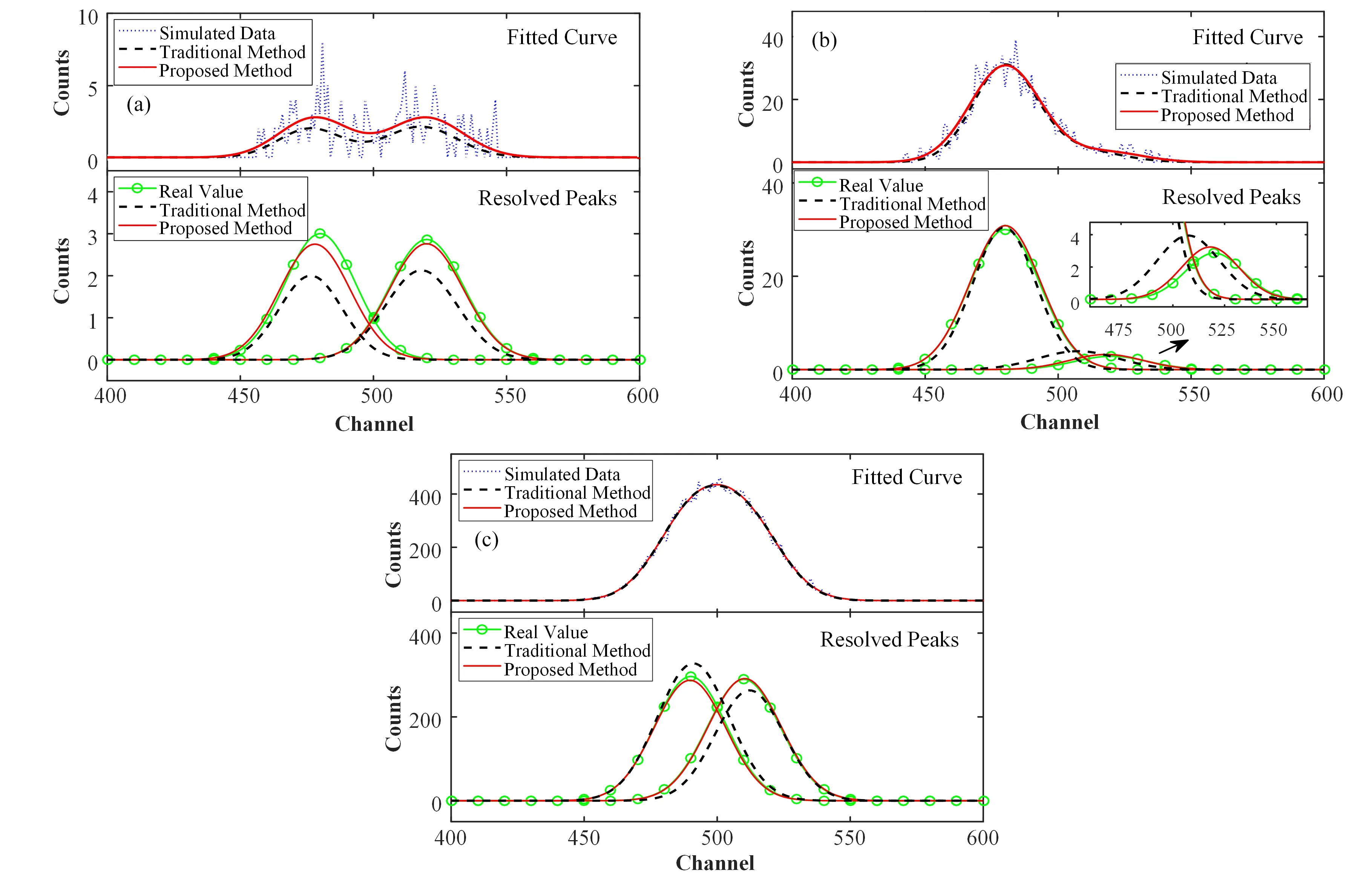
图1 不同条件下的仿真重峰数据及其解析结果示例(a)峰面积为100,峰间距40道,(b)左右两峰面积分别为1 000和100,峰间距40道,(c)峰面积为10 000,峰间距20道Fig.1 Examples of simulated data and analysis results under different conditions(a)The peak area is 100,the peak distance is 40 channels,(b)The peak area of the left and right peaks are 1 000 and 100 respectively,the peak distance is 40 channels,(c)The peak area is 10 000,the peak distance is 20 channels

图2 峰参数解析误差随峰面积的变化情况(a)平均峰位误差,(b)平均FWHM误差,(c)平均峰面积相对误差,(d)平均目标函数值Fig.2 Variation of peak parameter resolving errors with peak area(a)Average peak position error,(b)Average FWHM error,(c)Average peak area relative error,(d)Average objective function value
2.2 峰间距的影响
固定两个高斯峰的峰面积为10 000,研究峰间距(10~30道)对于解析结果的影响。由于第500道的FWHM值为32.1道,以此为基准,峰间距变化范围为0.31~0.93倍FWHM。图3(a)、图3(b)和图3(c)分别为峰位、FWHM和峰面积的平均误差随峰间距的变化情况。峰间距越小,解析复杂度和难度就越大。因此随着峰间距的减小,两种方法的误差逐渐增大。与图2中的结果类似,本方法的误差低于传统方法,在峰间距为10道,即0.31倍FWHM时,峰位误差降低了77%,峰面积相对误差降低了72%。

图3 峰参数解析误差随峰间距的变化情况(a)平均峰位误差,(b)平均FWHM误差,(c)平均峰面积相对误差,(d)平均目标函数值Fig.3 Variation of peak parameter resolving errors with peak distance(a)Average peak position error,(b)Average FWHM error,(c)Average peak area relative error,(d)Average objective function value
2.3 峰面积比的影响
固定两个高斯峰的峰位分别为480道和520道,分别称之为峰1和峰2。固定峰1的面积为1 000,改变峰2的面积,范围由100~10 000,即峰2与峰1的峰面积比的范围为0.1~10。
图4 (a~f)分别为解析得到的两个峰的峰位、FWHM和峰面积的平均误差随峰面积比的变化情况。可以看出,对于峰2,由于其峰面积一直在增大,峰参数解析误差呈现出随峰面积增大而减小的趋势,与图2中结果一致;峰1的情况与峰2相反,其峰参数误差随着峰面积比的增大比呈现出增大的趋势。可见,虽然峰1的面积一直固定,但是附近峰的峰面积增大同样会导致峰1的解析误差增大,这说明在强峰背景下,弱峰的解析难度较大。当峰1和峰2的面积分别为1 000和100时,相比于传统方法,本方法解析的峰1和峰2的峰位误差分别降低了26%和49%,峰面积相对误差分别降低了60%和59%。
3 实验验证
为了验证该方法对实测谱的解析能力,分别采用SAINT-GOBAIN公司的BrilLanCeTM380 76S76/3.5型LaBr3(Ce)探 测 器 和CANBERRA公 司 的BICRONTM802-3X3型NaI(Tl)探测器,配合ORTEC digiBASE-E数字多道,获取实测能谱。两个探测器在661.7 keV的能量分辨率分别为3.1%和7.3%。实验用放射源为152Eu和133Ba点源,活度分别约为7 000 Bq和25 000 Bq,源与探测器的距离为25 cm,能谱测量时间为30 min。其中,使用LaBr3(Ce)探测器 测 量 了152Eu的γ能 谱,并 对 其1 085.8 keV、1 112.1 keV射线[23]的2重峰区进行解析,得到的拟合曲线和重峰解析结果分别如图5(a)和图5(b)所示;使用NaI(Tl)探测器测量了133Ba的γ能谱,并对其276.4 keV、302.9 keV、356.0 keV和383.8 keV射线[23]的4重峰区进行解析,得到的拟合曲线和重峰解析结果分别如图5(c)和图5(d)所示。与图1中的结果类似,在图5(a)和图5(c)中,传统方法和本方法得到的拟合曲线非常接近,且都与实测谱保持一致;但是由图5(b)和图5(d)可以看出,两种方法解析出的全能峰,特别是133Ba重峰区内较弱的三个峰,存在较为明显的差别。

图4 峰参数解析误差随峰面积比的变化情况(a)峰1的平均峰位误差,(b)峰2的平均峰位误差,(c)峰1的平均峰面积相对误差,(d)峰2的平均峰面积相对误差,(e)峰1的平均FWHM误差,(f)峰2的平均FWHM误差Fig.4 Variation of peak parameter resolving errors with peak area ratio(a)Average peak position error of peak 1,(b)Average peak position error of peak 2,(c)Average peak area relative error of peak 1,(d)Average peak area relative error of peak 2,(e)Average FWHM error of peak 1,(f)Average FWHM error of peak 2
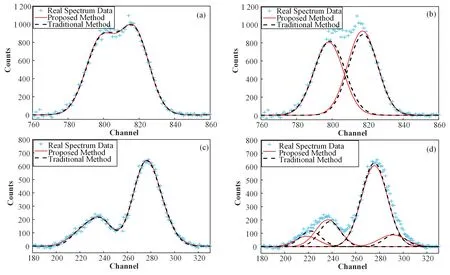
图5 实测γ能谱重峰解析结果(a)152Eu能谱2重峰拟合曲线,(b)152Eu能谱2重峰解析结果,(c)133Ba能谱4重峰拟合曲线,(d)133Ba能谱4重峰解析结果Fig.5 Overlapping peak analysis results of measuredγspectrum(a)Fitting curve of 2 overlapping peaks in 152Eu spectrum,(b)Resolved 2 overlapping peaks in 152Eu spectrum,(c)Fitting curve of 4 overlapping peaks in 133Ba spectrum,(d)Resolved 4 overlapping peaks in 133Ba spectrum

表1 实测γ能谱重峰的峰位和FWHM解析结果Table 1 Peak position and FWHM analysis results of measured spectra

表2 实测γ能谱重峰的峰面积解析结果Table 2 Peak area analysis results of measured spectra
表1 列出了解析得到的峰位和FWHM,表2列出了解析得到的峰面积。在表1和表2中,为了评价解析质量,利用国际原子能机构(International Atomic Energy Agency,IAEA)提供的放射性核素数据库[23],获得了152Eu和133Ba的γ射线能量和分支比信息;再利用谱仪系统的能量刻度和FWHM刻度信息,确定了各个全能峰的峰位、FWHM和峰面积的参考值。其中,峰面积与γ射线的分支比和谱仪的探测效率有关,由于重峰区内射线能量接近,探测效率变化不大,因此主要考虑峰面积与射线分支比的对应关系。因为准确的峰面积值无法获得,所以在每个峰区内,将分支比最大的峰作为基准,计算其它峰与该峰的峰面积比,用于评价峰面积的准确度。此外,除了1 085.8 keV和1 112.1 keV射线,152Eu核素还有一个1 089.7 keV的γ射线,分支比为0.017 3,在LaBr3(Ce)能谱中无法与1 085.8 keV射线区分,因此在计算峰面积比时将1 089.7 keV射线也考虑在内,如表2所示。
由表1整体看来,传统方法解析实测谱的峰位和FWHM与参考值误差较大,特别是存在低能量峰的FWHM值大于高能量峰的FWHM值的情况,不符合实际规律;而本方法解析的峰位和FWHM的准确度在多数情况下优于传统方法。
表2 中两种方法解析的峰面积比的相对误差如图6所示,本方法的峰面积比相对误差相比于传统方法平均降低了80%。NaI(Tl)探测器的能量分辨性能相对较差,而133Ba的4重峰区由于峰个数多,计数相对较少,且峰面积差别大,解析的难度较大。可以看出传统方法对其解析的峰面积误差明显大于152Eu的2重峰区;而本方法对两个峰区解析的峰面积误差没有明显区别,都保持在较低水平。该结果验证了本方法比传统方法解析复杂能谱的能力更强。

图6 峰面积比的相对误差对比Fig.6 Comparison of the relative errors of peak area ratio
4 结语
γ能谱重峰的解析受到统计涨落、峰间距、峰面积比等多种因素的影响。实验结果表明:较高的统计涨落水平、较小的峰间距、较大的峰面积差距以及较多的重峰个数都会导致重峰解析问题复杂度和难度的增加。
得益于对峰宽刻度等已知信息的充分利用,在处理高复杂度、高统计涨落的能谱数据时,通过将非线性拟合的结果约束在更准确的范围内,可有效提高重峰解析的精度。这说明,尽可能多地利用已知的物理条件或先验知识,为拟合问题增加约束,有利于增强抗统计涨落能力,使结果收敛到更准确的位置。
在传统重峰拟合解析方法中,往往把拟合残差等作为判断拟合结果好坏的依据。然而,残差实际上反映的是由拟合结果重建的曲线与测量数据在整体上的吻合程度;本文研究结果表明,残差值小并不能充分说明拟合结果与真实值的误差一定小。因此,对解析结果的评价除了要考虑拟合残差外,还要考虑其是否与已知条件一致,是否符合实际的物理规律。单纯追求残差最小化,容易陷入过拟合。
应该注意到,本方法适用于NaI(Tl)、LaBr3(Ce)等具有对称的高斯峰形的探测器。对于HPGe、CdZnTe等半导体探测器,其谱峰一般具有明显的低能拖尾,在使用本方法时应根据峰形特点调整约束条件。

