波纹场和新经典撕裂模对托卡马克中快离子输运影响的数值模拟研究
刘 锦 陈嘉盈 常悦悦 詹 研 虞立敏
(华东理工大学理学院上海200237)
化石能源的枯竭是人类必须面对的问题,可控核聚变为人类解决能源危机提供了一个可能的思路。托卡马克是当前热门的可控核聚变装置[1-2]。受控磁约束核聚变领域一个重要的问题是如何更好地约束快离子,通常扰动场(包括装置本身固有的波纹场和不稳定性产生的扰动场)引起快离子再分布和损失,而快离子损失不仅会降低等离子体温度,降低聚变反应率,而且也会损伤装置器壁,影响装置的寿命。因此研究快离子的输运和损失的物理机制对提升核聚变装置中等离子体性能和延长装置寿命有重要的意义[3-5]。
波纹扰动和新经典撕裂模(Neoclassical Tearing Mode,NTM)对快粒子输运乃至对装置运行造成重要影响,因而得到广泛的研究。波纹扰动指由于环向场线圈有限,有线圈的地方磁场大、无线圈的地方磁场小导致的类似波纹的环向场[3,6-7]。Wu等[8]使用ORBIT和NUBEAM/TRANSP代码计算了不同中性束注入方式下的束离子瞬态损失和波纹损失,提出波纹损失的主要过程是捕获粒子拐点径向漂移引起的波纹随机扩散,以及提高等离子体电流可以有效减少离子损失;李吉波[3]利用ORBIT模拟了不同的等离子体电流、快离子螺距角分布等因素对波纹损失的影响,得出等离子体电流较小和快离子螺距角较大的时候,损失份额较大;Nave等[9]研究了离子回旋射频(Ion-Cyclotron Radio Frequency,ICRF)加热下的等离子体中波纹场振幅由0.08%~1.5%的情况,研究显示:由于热离子和快离子的输运产生的扭矩会引起等离子体反向旋转。
NTM是在经典撕裂模(TM)上发展而来。TM考虑了q=m/n磁面以内的区域有限电阻效应和惯性效应,NTM额外考虑了自举电流[10]。Strumberger等[11]计算了中性束注入下由NTM和波纹场引起的快离子损失,发现NTM造成的通行粒子损失集中在tloss=40~200μs,造 成 的 捕 获 粒 子 损 失 集 中 在tloss≥200μs,波纹场造成的捕获粒子损失集中在tloss≥35μs,而波纹场几乎不影响通行粒子;Gobbin等[12]利用ORBIT模拟还原了ASDEX Upgrade中的NTM引起的磁岛效应,提出NTM不仅增加了损失粒子总量,并且使损失粒子通量集中在一个更小的区域;Zhang等[7]在对NTM和波纹场的研究中得出粒子在NTM和波纹的共同作用下会产生更大的轨道漂移,尤其是当粒子更多或更长时间地通过磁岛中心时;Bardóczi等[13]利 用TRANSP-‘Kick’输 运 模 型 对NTM进行的模拟研究,发现相空间中重叠共振会导致快离子在重叠岛链间的混沌运动,重叠共振在磁岛边缘产生且造成快离子损失。
本文主要使用数值模拟的方法,依靠导心运动代码ORBIT[14],研究波纹扰动和新经典撕裂模(NTM)对快粒子输运的影响。我们计算带1个正电荷,质量为2个质子质量的氘离子,采用NTM的模数为m/n=2/1(其中:m为极向模数;n为环向模数)和全超导托卡马克核聚变实验装置(Experimental and Advanced Superconducting Tokamak,EAST)中的波纹场模型,对不同参数情形下粒子损失和环向角动量扩散展开了研究。
1 计算方法
1.1 ORBIT程序理论模型
根据漂移动力学哈密顿理论,可以得到ORBIT代码采用的微分方程模型为[14-15]:

式中:H为带电粒子的动能和静电势能之和;Φ为静电势能;ρ//为归一化的回旋半径;μ为磁矩;g正比于ψp外的等离子体极向电流;I正比于ψp内环向总电流。在磁面坐标系下,θ是极向角,ζ是环向角,ψp为极向磁通,ψ为环向磁通。平衡磁场表示为
1.2 NTM扰动模型
ORBIT中可以处理的扰动形式为:

式中:ω是扰动的角频率,根据低频NTM的情形[16-17],本文分别对频率f为0 kHz、3 kHz、6 kHz、9 kHz的情况进行了讨论;m和n分别代表了扰动在极向和环向的模数,下面计算中我们取m/n=2/1。
模的径向结构使用解析表达式[18]:

式中:ψw是等离子体边界的极向磁通;ψp是r处的磁通;α0是扰动的幅度。扰动的形状类似钟形曲线。扰动的最大值等于α0,扰动磁场δBr最大值出现位置受安全因子q(r)的控制,出现在q(r)=m/n=2处[10]。
扰动幅度α0的选取参考了文献[12]中根据实验磁岛宽度选取的方法。EAST上测量的磁岛宽度为Δr/a=0.15[19],本文中a=40 cm,则磁岛宽度应为6 cm。因此取α0=5×10-5,使得磁岛宽度与实验值相近。
1.3 波纹场模型
波纹扰动指由于环向场线圈有限,有线圈的地方磁场大,无线圈的地方磁场小导致的环线磁场不均匀性。波纹场可以表述为:

典型圆截面中,取:

式中:R0是波纹中心的大半径;br是托卡马克截面的椭圆率,对于本文的圆截面托卡马克,br=π/4。李吉波[3]对EAST中快粒子波纹损失做了详细的研究。为了贴合实际情况,式(5)的其余参数均选取文献[3]中EAST波纹同样的值:

1.4 平衡磁面
为了简化计算,本文采用解析数值平衡下圆截面托卡马克,大径R0=185cm,截面半径a=40 cm。在这种情况下,将平衡磁场分解为环向BT和极向Bp,则可以近似表示为:
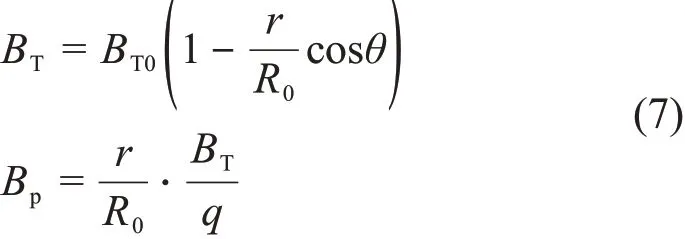
本文取BT0=1.8 T。式(7)中q=dψ/dψp,称为安全因子。平衡磁面如图1所示。
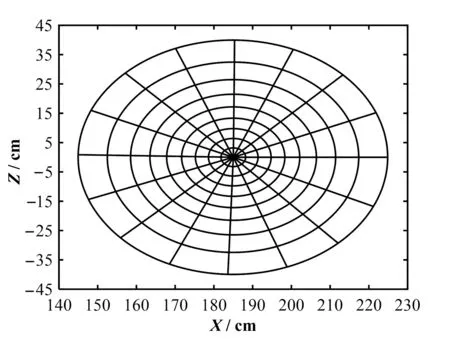
图1 平衡磁面Fig.1 Balanced magnetic surface
而安全因子采用三次曲线拟合的表达式,如下:
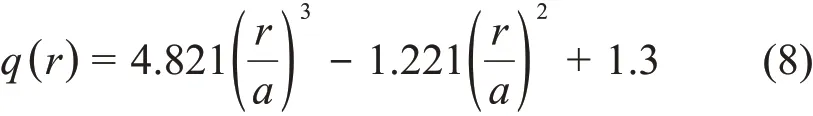
满足:

取α0=5×10-5时,安全因子q和δBr/B随归一化磁面的关系如图2。

图2 安全因子、模幅度和扰动磁场大小(a)安全因子和模幅度,(b)安全因子和扰动磁场Fig.2 Safety factor,mode amplitude,and magnitude of the disturbance magnetic field(a)Safety factor and mode amplitude,(b)Safety factor and disturbance magnetic field
1.5 其他条件
本文中计算采用的粒子是带一个正电荷、质量为两个质子质量的氘离子,不考虑粒子的碰撞和散射。
2 计算结果与讨论
2.1 扰动对粒子损失和扩散的影响
为了探究扰动对粒子损失数的影响,我们分为以下4类情况进行讨论,分别是无径向磁扰动、添加波纹扰动、添加NTM扰动以及同时添加波纹和NTM扰动。令α0=5×10-5,粒子能量为60 keV。初始粒子均匀分布在同一个磁面上,而投射角λ(v///v)相同。为了使计算结果收敛并节省计算时间,我们采用的粒子数目为3 000个。扫描的参数范围为:归一化的磁面从0.1变化到0.9、步长为0.1,投射角从0变化到0.9、步长为0.1。采用插值的方法绘制热力图来统计粒子的损失和扩散情况。其中,损失是指一旦粒子到达最外层磁面就认为发生损失,没有考虑粒子再回到等离子体的情形;而扩散则通过归一化的环向角动量(即Pζ/ψw,为了简洁记为Pζ)的方差来表示,设第i个粒子t时刻的环向角动量为Pζi(t),所有粒子t时刻的环向角动量的平均值为-Pζ(t),则有如式(10)[20]:
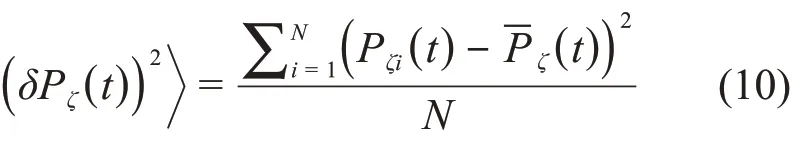
由于方差每个时刻都在变化,而最值得关注的是方差的最大值,因为它代表了粒子扩散程度最大的情况,因此取其所有时刻的最大值。

图3 中,横坐标为初始粒子的归一化磁面,纵坐标是初始粒子的投射角。颜色棒表明初始粒子在该磁面和投射角下最终损失粒子数,数值模拟使用了3 000个粒子,因此颜色棒最大值为3 000。图3(a)是没有加扰动情况下粒子损失情况,属于第一轨道损失。为了清楚扰动造成的粒子损失,在图3(b)、(c)、(d)中去除了第一轨道损失粒子。从图3(a)中可以得出,粒子靠外磁面、低投射角分布的情况下损失粒子数多,这和预期是一致的。低投射角意味着粒子平行速度分量小,有大的概率成为捕获粒子。磁面高意味着粒子初始位置接近托卡马克内壁,容易造成第一轨道损失。与没有添加任何扰动相比,添加波纹增加了低投射角、内磁面的粒子的损失并有跳变增加现象,添加NTM显著增加了磁面0.4~0.9下投射角大于0.4的粒子损失,磁面为0.4处剧烈的粒子损失是由于该磁面处于δBr极大值附近。而NTM和波纹都添加的损失情况近似于它们单独添加时造成损失之和。
环向角动量的扩散同样是我们关注的一个物理量,可以间接反映离子在扰动作用下的扩散情况。我们用粒子群运行所有时刻中全部粒子环向角动量的方差的最大值来描述。统计结果如图4所示。

图3 粒子损失统计图(a)没有径向磁扰动,(b)添加NTM,(c)添加波纹,(d)添加波纹和NTM((b)、(c)、(d)图中已去除第一轨道损失粒子)Fig.3 Particle loss statistics(a)Without radial magnetic perturbation,(b)With NTM,(c)With ripple field,(d)With both of ripplefield and NTM(First orbit losses have been removed in figure(b),(c),(d))
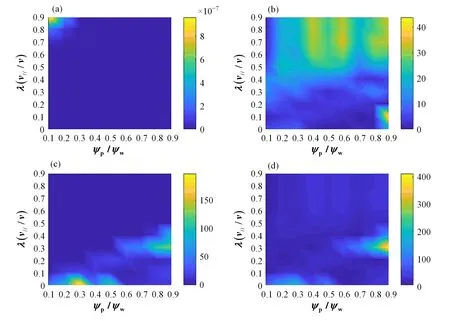
图4 ?统计图(a)没有径向磁扰动,(b)添加NTM,(c)添加波纹,(d)添加波纹和NTM Fig.4?statistics(a)Without radial magnetic perturbation,(b)With NTM,(c)With ripple field,(d)With both of ripple field and NTM
由上述讨论可知,波纹和NTM扰动并不是对所有粒子都有影响,而是分别对捕获粒子和通行粒子造成影响。我们分别计算了捕获粒子和通行粒子在这两种不同条件下的轨道。设初始粒子能量40 keV,捕获粒子初始磁面0.7,投射角0.3;通行粒子初始磁面0.7,投射角0.8。
图5 中显示了不同扰动条件下相同初始条件的粒子轨迹。在波纹影响下,捕获粒子轨道出现剧烈偏移,但是通行粒子轨道并没有发生明显变化。在NTM的影响下捕获粒子轨道同样出现偏移,但是程度不如波纹影响的剧烈。通行粒子的轨道线条同样变宽了,体现了NTM对通行粒子造成影响。当两者都叠加时,捕获粒子的轨道漂移更加剧烈,说明波纹和NTM的协同作用将造成更大的环向角动量扩散。单粒子运行的结果印证了波纹扰动对捕获粒子作用强烈,是捕获粒子环向角动量扩散增加的主要原因。这解释了图4中波纹场影响下环向角动量扩散在λ<0.5的区域特别强烈的现象。
2.2 扰动对不同相空间粒子的影响
为研究扰动对不同种类的粒子影响,我们分析了相空间中均匀分布的粒子的变化。高能粒子可以按其损失与否分为损失(Lost)和磁约束(Confined)。按照运动状态分为捕获(Trapped)、正向通行(Copassing)、逆 向 通 行(Counter-passing)和 停 滞(Stagnation)。用轨道分类图来表述这6种粒子的分布,横坐标为归一化环向角动量Pζ/ψw,纵坐标为归一化磁矩,如图6所示。
我们设置粒子能量为40 keV,选取初始粒子在相空间中均匀分布,调整NTM和波纹扰动的有无进行计算。从计算结果中,统计损失粒子和未损失粒子的初始相空间中的分布,得到如下的结果。
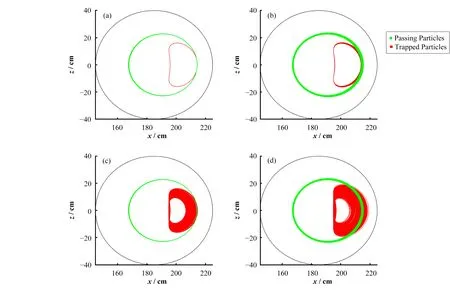
图5 通行粒子和捕获粒子轨道图(a)没有径向磁扰动,(b)添加NTM,(c)添加波纹,(d)添加波纹和NTMFig.5 Trajectories of passing particles and trapped particles(a)Without radial magnetic perturbation,(b)With NTM,(c)With ripple field,(d)With both
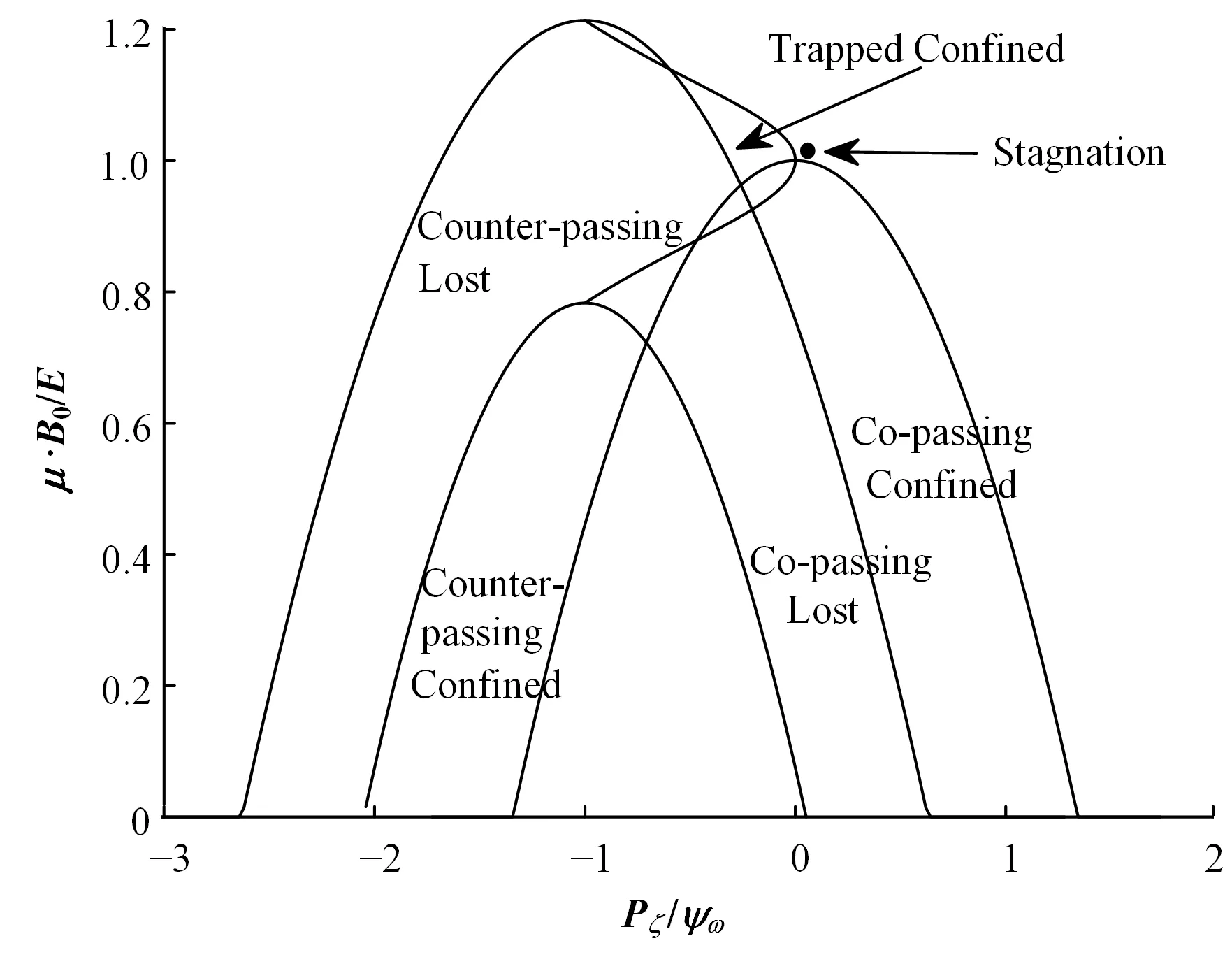
图6 不同类型的粒子在相空间分布Fig.6 Distribution of different types of particles in phase space
图7 中显示了某损失粒子和某未损失的粒子的初始相位。对比发现,在不加扰动的情况下,损失和未损失粒子按相位图的边界分布。加了NTM的情况下,逆向通行损失粒子和正向通行损失粒子开始入侵未损失粒子的边界。我们感兴趣的是随着扰动幅度α0增加,相位图会发生怎样的改变。于是在其他条件都相同的前提下,令粒子能量为40 keV,以便观察到宽的Trapped Confined区域。α0的变化区间从3×10-5变化到9×10-5,不添加波纹,观察粒子相位图的变化。如图8所示,随着扰动幅度的增加,位于Co-passing Confined和Counter-passing Confined区域的粒子逐渐损失,Trapped Confined区域也有同样的转变,但是比例明显小于其他区域。
同时,我们也发现波纹场的主要影响造成Trapped Confined区域内粒子大量损失。随着粒子能量的升高,Trapped Confined区域会越来越小,不难预见波纹场造成的影响会越来越小。为了证实这一观点,我们在运行中只添加了波纹,并改变粒子能量从40~120 keV,观察相位图变化。我们得到的结果如图9所示。
从图9(a)~(c)三幅图的变化规律中可以看到,随着粒子能量增加,波纹影响的区域越来越小,最后消失不见,说明粒子能量越高,波纹扰动的影响就越小。
2.3 加入NTM频率对损失和扩散的影响
上面的研究都是基于静态NTM扰动,但实际上大多数粒子都是在毫秒量级内损失,这和NTM的周期是同一个数量级[12]。因此需要考虑NTM的频率带来的影响。假设NTM以恒定频率旋转,我们设置频率为0 kHz、3 kHz、6 kHz、9 kHz,扰动幅度为α0=5×10-5,粒子能量为60 keV,不加入波纹场。同样做出粒子的损失和环向角动量扩散图。
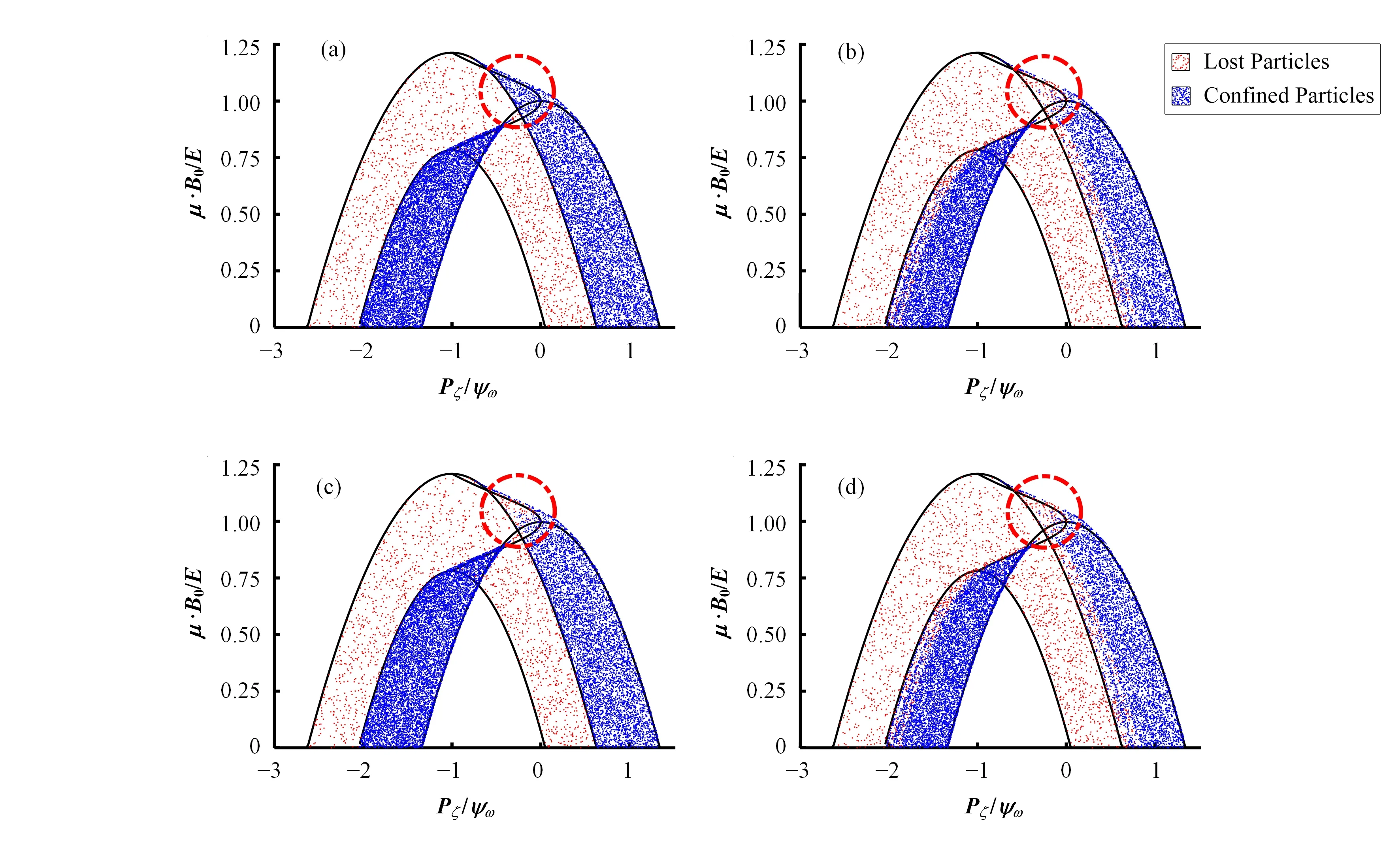
图7 损失粒子和未损失粒子的初始相位(a)没有径向磁扰动,(b)添加NTM,(c)添加波纹,(d)添加波纹和NTMFig.7 The initial phase of the lost and confined particles with(a)Without radial magnetic perturbation,(b)With NTM,(c)With ripple field,(d)With both.

图8 改变扰动幅度对相位图的影响(a)α0=3×10-5,(b)α0=6×10-5,(c)α0=9×10-5Fig.8 The effect of changing the amplitude of the disturbance on the phase map(a)α0=3×10-5,(b)α0=6×10-5,(c)α0=9×10-5
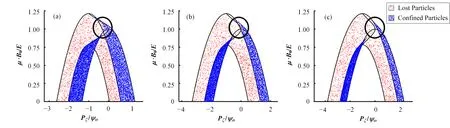
图9 只添加波纹,改变粒子能量,观察相位图变化(a)E=40 keV,(b)E=80 keV,(c)E=120 keVFig.9 The change of phase diagram caused by various particle energies when only ripple field is applied(a)E=40 keV,(b)E=80 keV,(c)E=120 keV
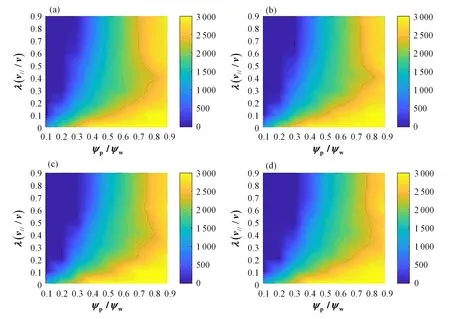
图10 NTM不同频率的粒子损失统计图(a)f=0 kHz,(b)f=3kHz,(c)f=6 kHz,(d)f=9 kHzFig.10 Statistics of particle loss at different frequencies of NTM(a)f=0 kHz,(b)f=3 kHz,(c)f=6kHz,(d)f=9 kHz

图11 NTM不同频率的统计图(a)f=0 kHz,(b)f=3 kHz,(c)f=6 kHz,(d)f=9 kHzFig.11 Statistics of at different frequencies of NTM(a)f=0 kHz,(b)f=3 kHz,(c)f=6 kHz,(d)f=9 kHz
从图10、图11中我们发现频率加入后,粒子损失情况保持了原有的特征,对初始磁面0.7~0.8、投射角大于0.4的范围,可以看到随着频率的提高,损失数量逐步减少。而对于环向角动量扩散情况,不变之处在于磁面从0.7~0.9、投射角0~0.2的范围有一个明显的高峰,这可能与该处粒子非常容易损失有关。对投射角大于0.4的区域,随着频率加入发生了明显的变化:原先的条带状分布被破坏,磁面为0.4和0.6的亮纹产生的混合、0.8处的亮纹逐渐减弱;浅蓝色区域增加,尤其是f=9 kHz的情形。这些迹象都表明NTM频率增加使得环向角动量扩散变得更加均匀。
3 结语
本文使用导心运动代码ORBIT,研究了波纹场和新经典撕裂模对圆截面托卡马克粒子输运的影响。计算发现,扰动能增加离轴、低投射角的快粒子的损失率。具体地,与没有添加任何扰动相比,添加波纹增加了低投射角粒子的损失,添加NTM显著增加了磁面0.4~0.9下投射角大于0.4的粒子损失,而两个都添加的损失情况近似于单独添加时造成损失之和。添加波纹会显著增加环向角动量扩散,而在NTM扰动最强的区域环向角动量扩散也相对显著,波纹扰动和NTM的对环向角动量扩散的协同作用远大于单独作用之和。波纹扰动对λ<0.5的区域影响犹为剧烈,这部分粒子大多属于捕获粒子。从单粒子轨道图上,在波纹场影响下捕获粒子轨道发生偏移,其程度远大于NTM单独作用导致的偏移。证明了波纹扰动是造成粒子环向角动量扩散的主要原因。
在相位图上,位于同向通行约束和反向通行约束区域的粒子会受到NTM影响而损失,波纹场会造成磁捕获约束区域内粒子大量损失。随着粒子能量升高,磁捕获约束区域变小,波纹扰动的影响就越小。
当考虑NTM频率时,粒子损失情况基本保持原始特征,但是对初始磁面0.7~0.8、投射角大于0.4的范围,随着频率的提高,损失粒子数量逐步减少。同时我们还发现,NTM频率增加使得环向角动量扩散变得更加均匀。
我们的工作研究了波纹场和2/1 NTM对不同初始状态粒子的作用情况,对托卡马克装置的设计、高能粒子的约束都有参考价值。后续还将从托卡马克截面的设计、安全因子曲线的选取等方面做进一步研究。

