滑块碰撞动力学与圆周率的关联1)

李开玮

(广东理工学院工业自动化系，广东肇庆526100)

滑块碰撞是牛顿力学中常见的问题，一般通过动量守恒和能量变化的关系去研究碰撞过程；而圆周率π 是几何数学的问题，为圆的周长与直径之比，历史上我国数学家刘徽通过割圆术算出π 的小数点后第5 位3.14159，之后数学家们计算出的小数点后位数越来越多[1-2]。π 的数字为：3.14159265358979-323846264338327950288419716939937510···，滑块碰撞与这两者看起来毫无联系，但有趣的是，作者在研究碰撞问题时，发现滑块的碰撞次数与π 极其相似，并分析了它们的内在关联。

1 问题来源

如图1 所示，水平光滑的地面上放置小木块m，大木块M，左端是固定的墙壁，初始时刻m静止，M以初速度v0向左运动，将与m发生碰撞，之后m获得速度向左运动，将与墙壁发生碰撞反弹，所有碰撞均没有动能损失，求碰撞次数。

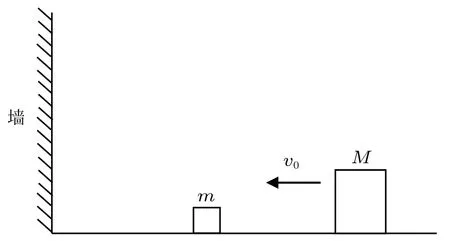
图1 问题示意图

解析：首先考虑最简单情况，若两滑块质量相等m=M，则M向左运动第一次与m碰撞，根据动量守恒和能量守恒，将发生速度传递，接下来m以v0向左运动与墙壁第二次碰撞，速度反向向右，大小不变，之后向右运动，与M第三次碰撞，m停止，M以v0向右运动。总碰撞次数为3。

接下来讨论滑块质量不相等的情况，设M/m=k，以水平向左为正方向，为了描述的需要，称两滑块之间的碰撞为碰撞，称m 与墙壁的碰撞为反射，设第n 次碰撞(包括反射) 后，m 与M 速度分别为un和vn，对第一次碰撞，根据动量守恒和能量守恒有

解式(1) 得

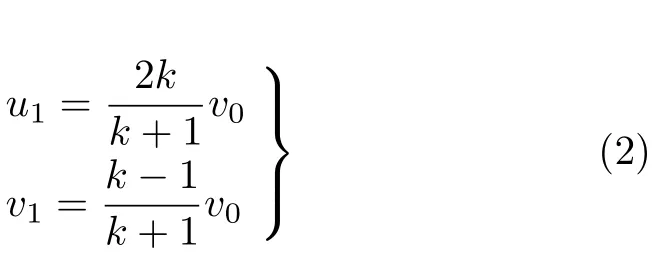
接下来m 与墙壁发生第一次反射，速度变为

第一次反射后，m 将向右运动与M 发生第二次碰撞，同样根据动量守恒和能量守恒

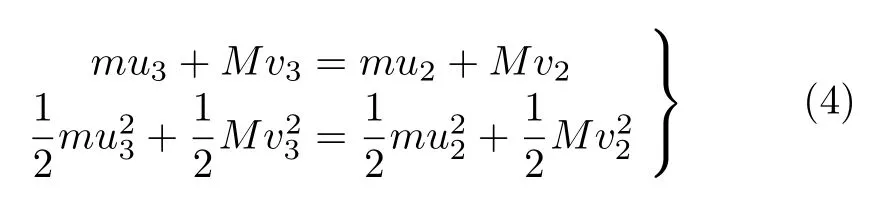
解式(4) 得

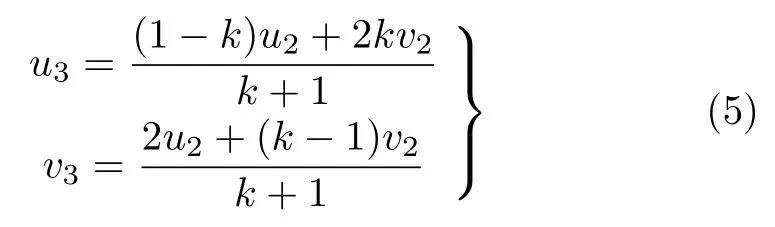
将un，vn写成向量(unvn)，式(3) 和式(5) 可变为矩阵运算形式

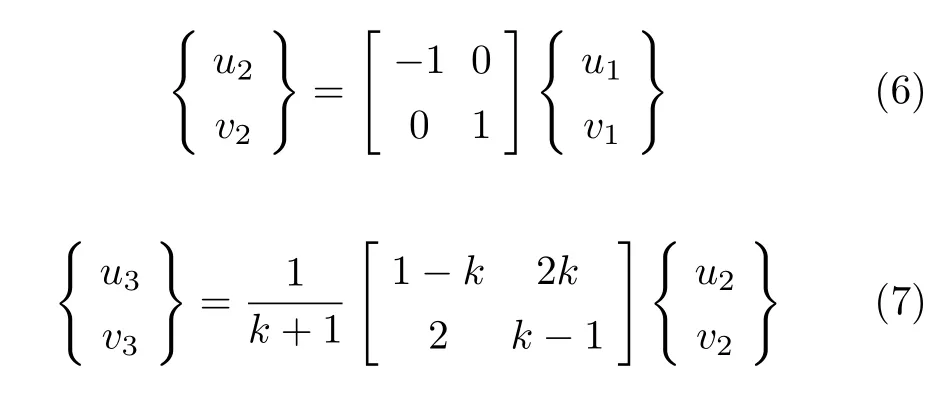
对比式(2) 与式(7)，发现式(2) 也可以写为类似式(7) 的样子

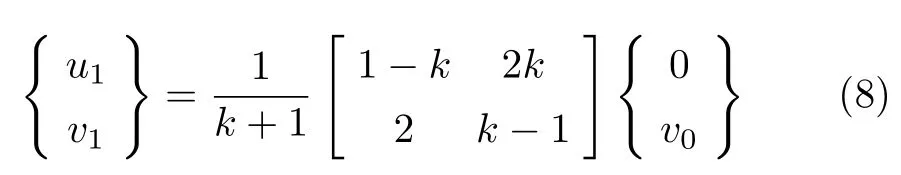
接下来第二次反射，第三次碰撞分别与式(3)和式(4) 类似，只需将式(3) 和式(4) 中速度下标加1，因此结论也与式(6) 和式(7) 相似，因此每次碰撞和反射后，两滑块速度向量变换矩阵分别为

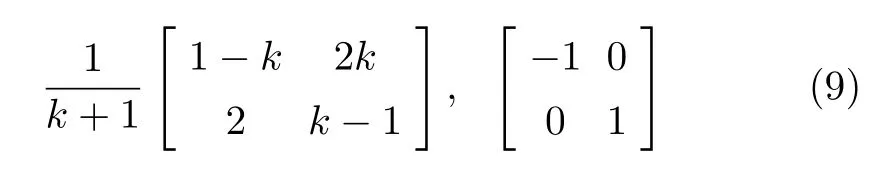
当两滑块碰撞后速度满足vn＜0 且|un| ＜|vn| 时，碰撞将不再发生。

根据式(1)～式(9)，作者编写了MATLAB 函数文件，如图2 所示，利用该函数文件，计算了不同k 值下的碰撞次数N_collide，如表1 所示。根据表1数据，发现当k =100N，N_collide 与圆周率π 的小数点后N 位数字一样。

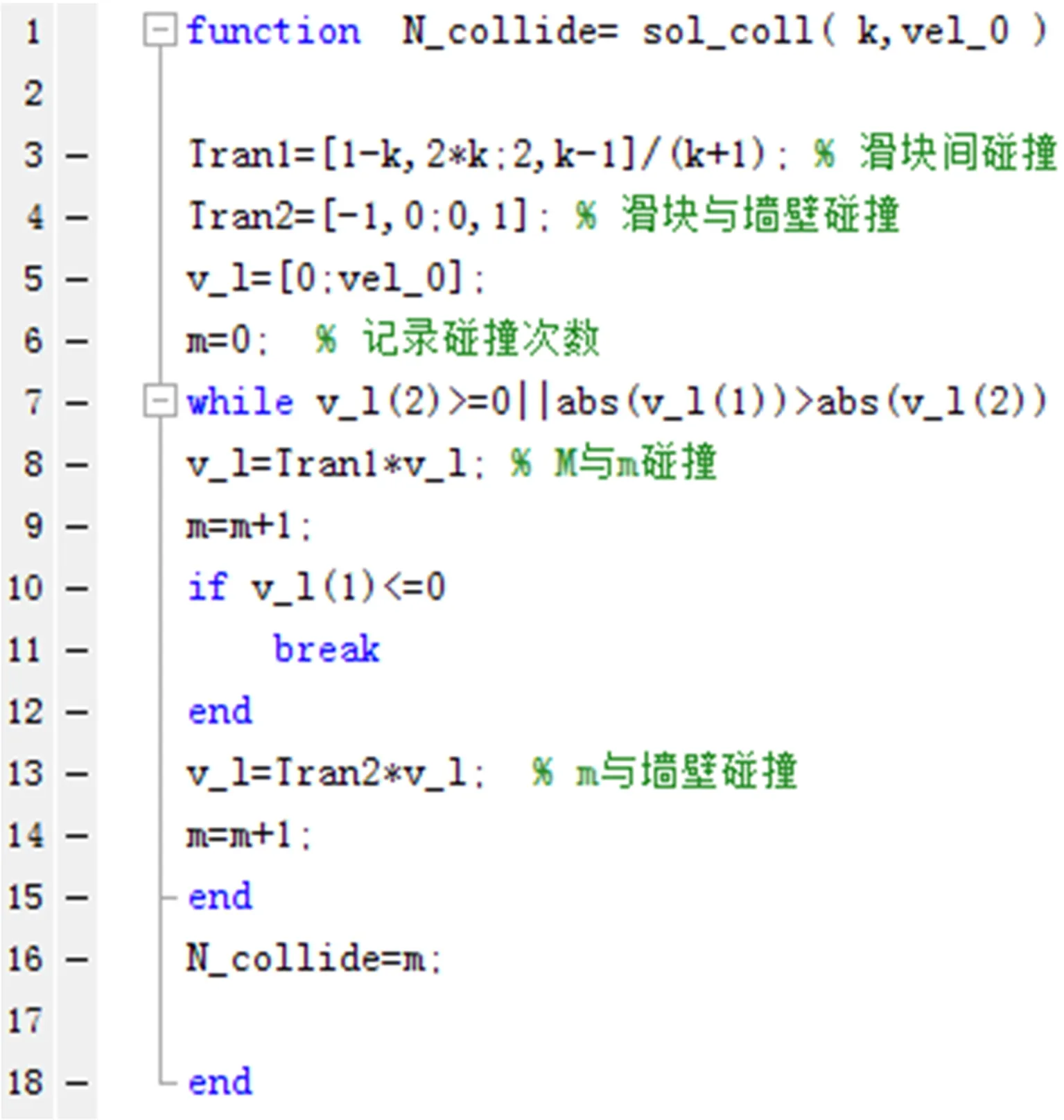
图2 MATLAB 函数文件

表1 碰撞次数随着k 的变化

2 理论证明

由表1 可以猜测，N_collide = [ (10N)·Pi]，[x]为小于x 的最大整数，接下来证明这个猜测。

以水平面与墙壁交点为原点，水平向右为正方向，设初始时刻，m 与M 位置为x0，y0，t 时刻m与M 位置为x(t)，y(t)，根据图1

当x(t)=0 时，m 与墙壁碰撞；当x(t)=y(t)时，m与M 碰撞。如图3 所示，点(x(t)，y(t)) 即可描述t时刻两滑块的位置，随着时间的推移，点(x(t)，y(t))的移动形成位置相空间的轨迹图。第一次碰撞前，m位置不变，M 向左运动，因此轨迹为竖直向下的直线，直至碰到直线y = x，发生碰撞，之后两滑块均向左运动，故x(t)，y(t) 均减小，轨迹变为斜向下，直至x(t) = 0，m 与墙壁碰撞反射，反射后m 速度反向，大小不变，因此在图像中有

之后，将发生第2 次滑块间碰撞，反射······。当第n 次碰撞后，轨迹直线方向为斜向右上方，且接近与y = x 平行时，将不再与y = x 相交，即碰撞结束，轨迹与y 轴、直线y = x 交点个数之和为碰撞发生次数。由图3 可知

根据式(12)可以计算出碰撞次数，但计算有点繁琐，主要是因为式(12) 中第二式涉及两滑块速度，而每次碰撞后，滑块速度均发生变化，为了计算的简单，接下来我们对相空间(x(t)，y(t))作一个变形，使式(12) 中第二式消失。

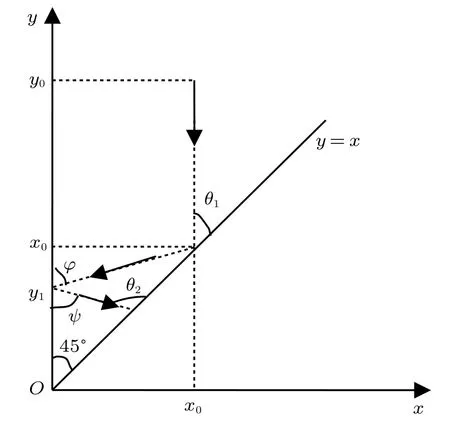
图3 两滑块相空间轨迹图

将(x(t)，y(t)) 变形为(X(t)，Y(t))，变换关系为

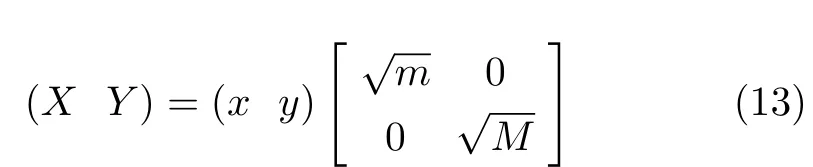
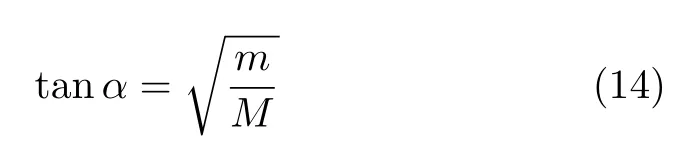
当m 与墙壁碰撞后，m 速度反向，故图4 中β1=β2，当两滑块碰撞时，如图4(a)，r 为直线Y =方向向量，w 为碰前入射向量，w′为碰后反射向量根据动量守恒，能量守恒式(4) 可以改写为

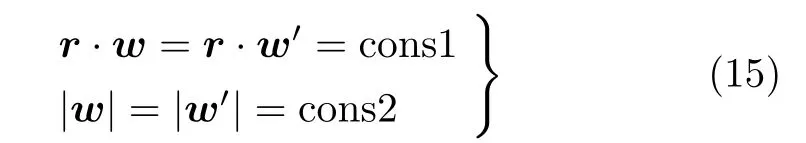
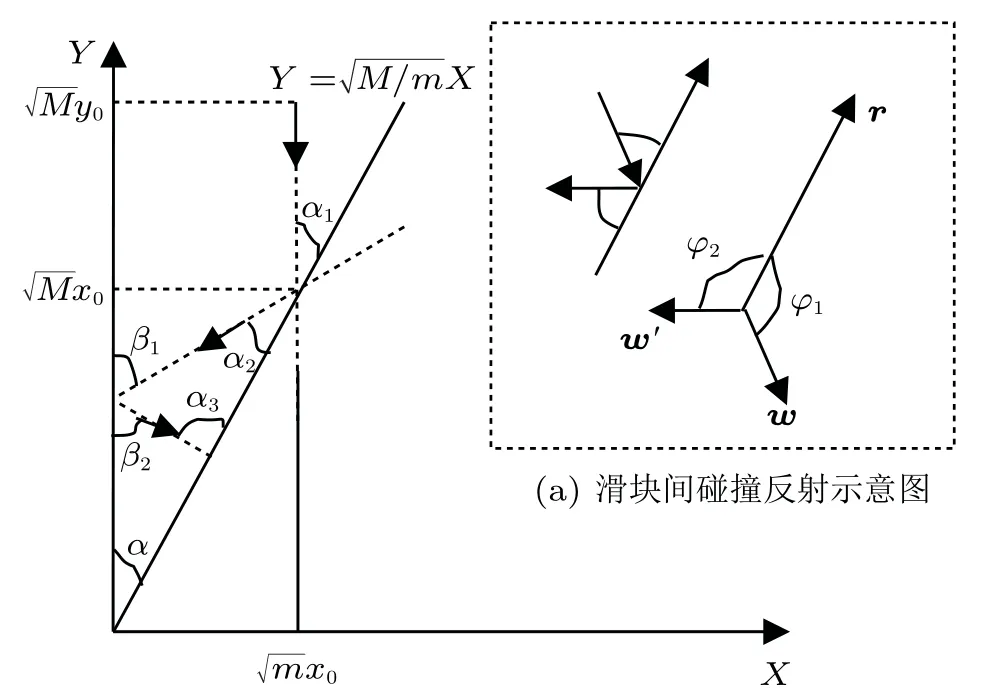
图4 X -Y 相空间轨迹图

由式(15) 可得入射向量w 与r 夹角同反射向量w′与r 夹角相等，即

由以上分析可以得到图4 中各个角度关系

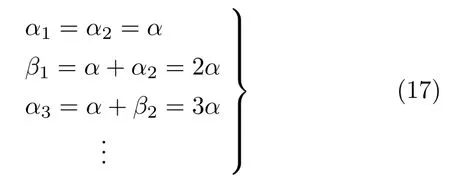
因此碰撞次数应为

由式(14) 和式(19) 可得

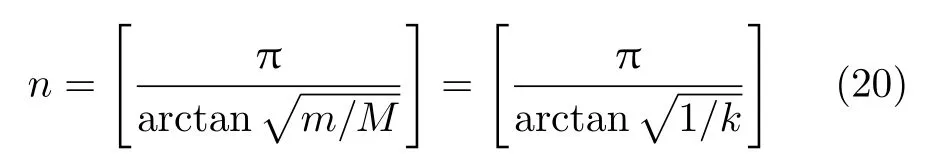
将k =100N代入式(20) 得

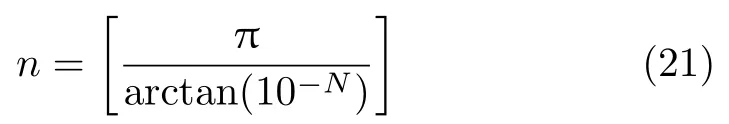
将arctanx在x=0 附近作泰勒展开可得

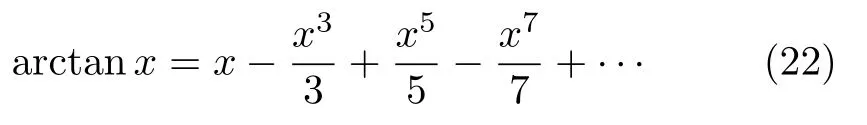
则

由式(23) 可得

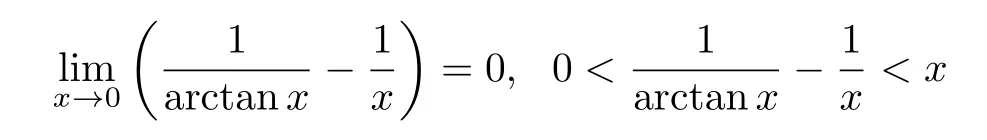
因此式(21) 变为n=[π·10N] 。

3 结语

本文通过MATLAB 计算了滑块碰撞次数，发现当k=100N，碰撞次数为[π×10N]，即碰撞次数与圆周率小数点后数字一样，并利用相空间轨迹法巧妙地证明了该联系。将力学过程用几何图像表示出来有助于清晰理解整个运动过程，使计算变得简化。