循环荷载作用下考虑Hansbo 渗流的饱和黏土固结分析
时 刚 朱邦华 张玉蓉
*(郑州大学土木工程学院,郑州450001)
†(郑州大学商学院,郑州450001)
传统的一维Terzaghi 固结理论广泛应用于求解饱和黏性土地基在有侧限应力状态下,外荷载作用时固结过程中任意时刻的固结度,适用于土中水的渗流服从Darcy 定律,土的渗透系数和压缩系数在渗流过程中保持不变的土体,且外荷载是一次瞬时施加的。然而越来越多的理论研究和实际工程表明,现代建筑如地铁隧道、铁路路基等大型轨道交通基础设施的地基所承受的往往不是瞬时施加的荷载,在单次列车经过的时候,考虑到每对车轮对轨道的冲击,可以近似看做是短期性的循环荷载;在隧道或铁路线寿命周期内,以列车为整体则可以看作是长周期性的循环荷载。伴随着建筑物防灾减灾研究的兴起,对地震作用产生的周期性荷载的研究也逐渐丰富。因此对于建筑物基础设施下的地基固结变形问题,传统的一维Terzaghi 固结理论存在较大的局限性。随着时代的发展,对于在各种典型周期性循环荷载作用下的各类地基变形问题,越来越多的学者进行了研究。有研究结果显示,在不同的循环荷载作用下,黏土地基的应变量都呈现出先迅速沉降,后增长逐渐变缓,最终逐步趋于稳定,在不同的循环周期后,循环周期与累计应变量之间存在线性关系[1]。而且在周期性循环荷载作用下,随着循环荷载的变化,土体中各点的有效应力并不随之同步变化,而是按照某种规律滞后发展,最终达到一种稳定循环状态[2]。蒋军等[3]提出土的固结变形在周期性循环荷载作用时由可逆变形和不可逆变形两部分组成。同时,李西斌等[4]也提出孔压和固结度在循环荷载的一个周期内都会达到极值一次,并运用积分的方法给出了固结方程的解析解。
随着近年来工程实际需求和对渗流固结问题的深入研究,Darcy 渗流的局限性也越来越明显[5-6]。在此基础上,李传勋等[7-9]和Li 等[10]指出结构性软土的固结速率在考虑非Darcy 渗流的情况下要比考虑Darcy 定律慢,且固结速率随着非Darcy 渗流模型参数的增大将显著降低。而刘忠玉等[11-12]和孙丽云等[13]的研究也表明了饱和黏土中地基的沉降速率和整体孔隙水压力消散速率受土中孔隙水渗流的非Darcy 特性影响将显著延缓,随着Hansbo 渗流参数的增大,这种影响会更加明显,同时地基固结沉降的速率与循环荷载周期有关,循环荷载周期越短,则固结沉降速率也会越慢。如果考虑到起始水力梯度的影响,以应力表示的平均固结度最终将稳定在一个小于100%的范围内,最终的平均固结度随着起始水力梯度的增大会减小;固结完成时的孔隙水压力随着初始孔隙水压力增大将消散的越充分[14]。基于对非Darcy 渗流模型的深入研究,董兴泉等[15]和郑辉等[16]分析了非Darcy 渗流下大、小变形不同几何假定下对固结沉降的影响,结果显示固结速率在大变形假定下比小变形假定下快。
另一方面,在土的修正剑桥模型基础上,姚仰平等[17]和胡晶等[18]提出了应力路径无关的统一硬化参数(UH(unified hardening)模型),把时间、循环加载和温度等因素作为变量,引入到UH 模型中,建立了一系列扩展UH 模型。该模型所选用的各项土体参数与修正剑桥模型参数完全相同,便于考虑多种外部因素、复杂特性、复杂加载条件等的影响,广泛应用于岩土工程问题的分析中。在工程实践中,地铁隧道、铁路轨道等建筑也广泛建造于黏土地基上,其建筑地基往往受到周期性循环荷载的作用,此时,地基土层中的超孔隙水压力在周期性循环荷载作用下也呈现周期性变化。因此,本文在Hansbo 渗流模型和UH 本构模型的基础上,建立了以超孔隙水压力u为变量的周期性循环荷载作用下饱和黏土渗流固结方程,在对固结方程进行求解计算中采用FlexPDE软件。在此基础上,研究了饱和黏土在周期性循环荷载作用下的渗流固结特性,初步讨论了UH 模型参数、Hansbo 渗流参数、循环荷载周期和循环荷载类型在渗流固结过程中的影响。
1 基本假定及固结方程的建立
1.1 问题的数学描述
如图1 所示,设存在一个顶面是透水面,底面是不透水面的饱和黏土层且厚度为H0。均布循环荷载q(t) 作用在饱和黏土层顶面上,周期设为Tc,荷载最大值qmax,在该均布循环荷载作用下土层开始固结。
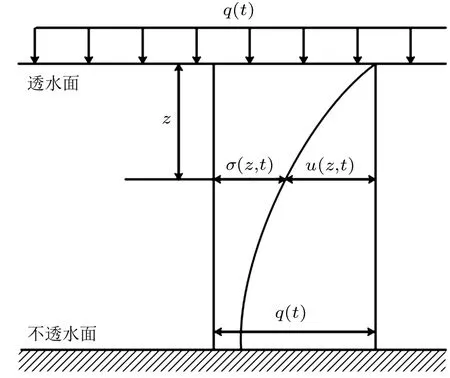
图1 循环荷载作用下土体一维固结示意图
1.2 基本假定
饱和黏土在循环荷载作用下的固结问题是个复杂的问题,为了便于建立饱和黏土在考虑Hansbo 渗流时的一维渗流固结的数学模型,对计算过程进行简化分析,给出以下基本假定:
(1) 饱和黏土中水的渗流规律遵循Hansbo 渗流模型,且在固结过程中Hansbo 渗流模型中给定的参数m 和i1保持不变。

式中,v 为孔隙水的渗流速度;K 为渗流初始段指数渗流的渗透系数;i 为水力梯度;m 为实验中确定的常数;i1为渗流的起始水力梯度;i0为渗流计算起始水力梯度,有
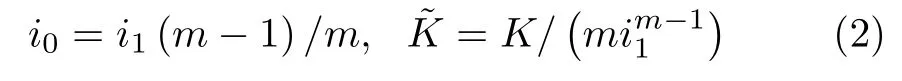
(2) 饱和黏土层中的孔隙水和土颗粒均不可压缩,且在自重应力作用下,土层已经完成固结,处于正常固结状态。
(3)土体仅在竖直方向上出现渗流和变形,遵循一维渗流固结的基本假定。
(4) 土体具有可采用流变模型来描述的流变特性。
1.3 数学模型的建立
首先从引入UH 本构模型的应力-应变关系推导开始,逐步考虑循环荷载条件、Hansbo 渗流和一维流变固结理论,最后综合分析得出循环荷载作用下基于UH 本构模型和考虑Hansbo 渗流的一维固结方程。
由文献[17-18] 可知,在UH 模型中,一维竖向应变增量表达式当dσ′z>0 时,有

当dσ′z≤0 时,有

式中,e0是土的初始孔隙比,Cs是土的回弹指数,Cc是土的压缩指数,M 是临界状态应力比,Mf是潜在破坏应力比,σ′z是竖向有效应力,Cα为土的次固结系数,tα为老化时间,t0为单位时间。
临界状态应力比和潜在破坏应力比之间可表示为
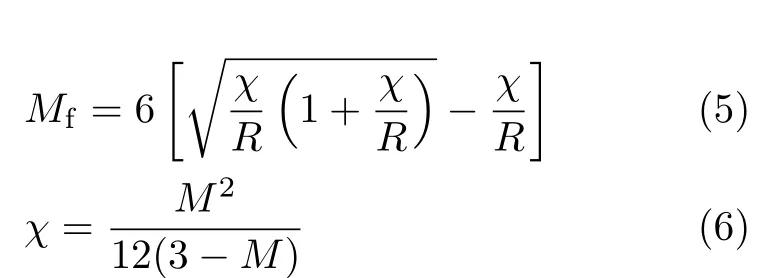
超固结参数可表示为

式中,R 为超固结参数;σ′c0类似于前期固结压力,为瞬时圧缩线与回弹线交点的竖向压力;当不考虑时间效应时,σ′c0即为前期固结压力,超固结比即初始超固结参数的倒数。
有效应力可表示为

水力梯度i 可表示为

为了便于进行饱和黏土一维流变固结方程的推导,在太沙基一维固结方程推导过程的基础上。根据渗流连续性条件,有

将式(1)~式(4) 代入式(12) 得
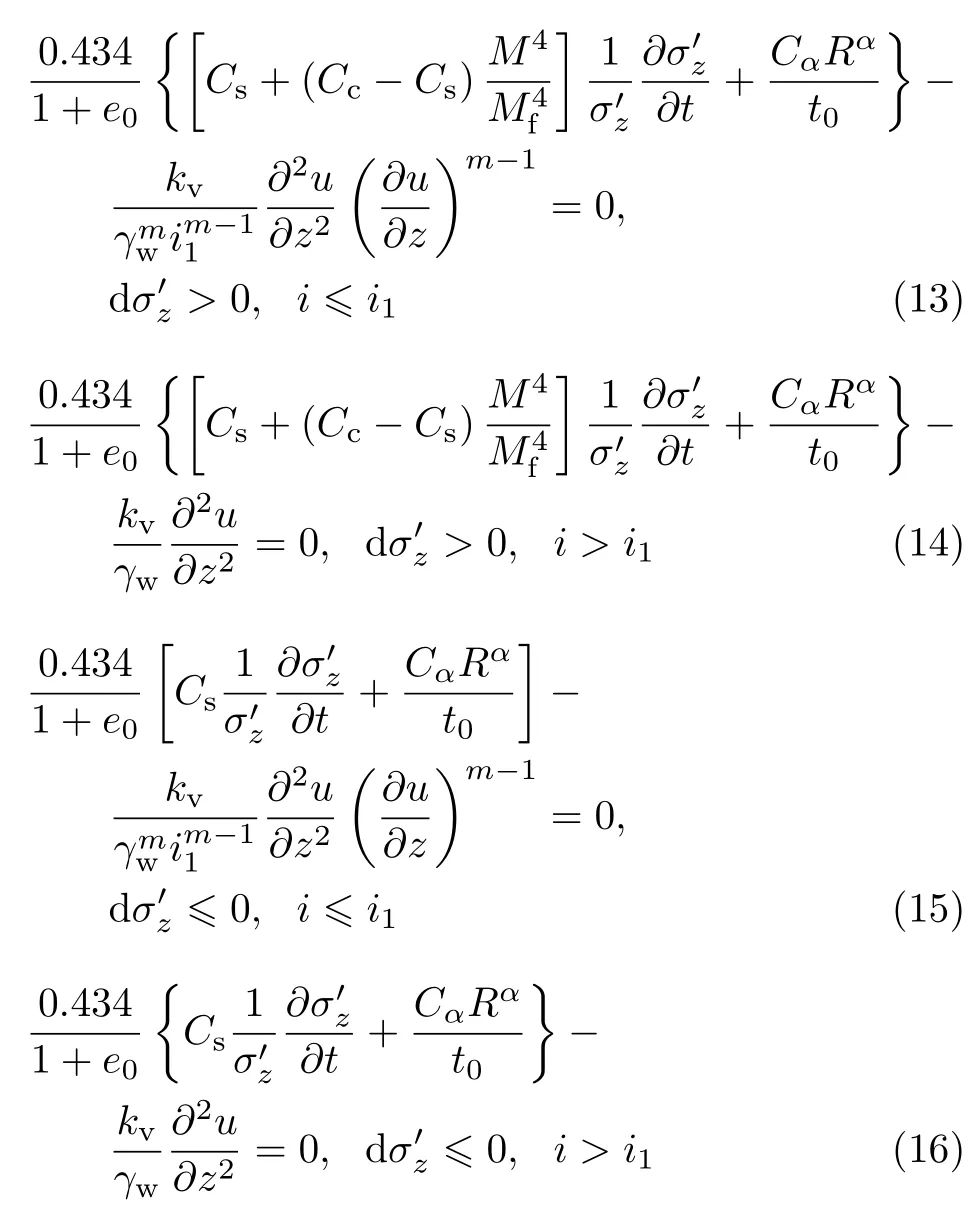
其中,方程的初始条件为
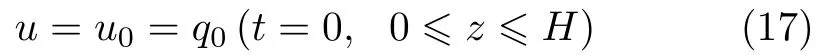
方程的边界条件为

以孔压定义的平均固结度为
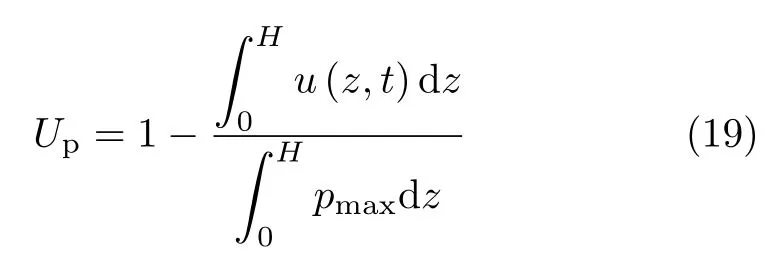
以应变定义的平均沉降量为

其中,εv为竖直方向上土体的应变。
2 FlexPDE 求解方程及算法验证
2.1 渗流固结方程的求解
上述方程直接计算十分复杂,难以求得具体的解析解,已有研究求解该问题时多采用传统的有限差分法和有限体积法,并给出解答[12-13]。与其他研究不同,本文在求解小变形固结方程时采用了Flex-PDE 软件。
FlexPDE 软件是一款采用有限元方法编程的广泛应用于偏微分方程求解的软件。该软件操作简洁明了,计算流程比较人性化,描述所研究问题的偏微分控制方程、求解域及其初始条件和边界条件时仅需非常简洁的程序语言,使科研人员和工程施工人员的精力主要集中于所需要研究分析的问题中数学模型的建立和关键控制方程的推导,从而节省大量用于计算和编写计算程序的时间,显著降低了工程实践中经常遇到的复杂工程地质问题的研究门槛,具有较强的工程推广意义。
2.2 算法验证
根据现有研究,当q(t)= const 时,本文描述的固结问题与文献[19] 的计算验证相同,将文献[19]计算验证中的一维固结问题应用本文方法计算,对比结果如图2 所示。由图2 可知,本文采用Flex-PDE 软件的计算结果与文献[19]计算的沉降曲线基本相互重合,从而验证了本文所采用的数值计算方法的可靠性。
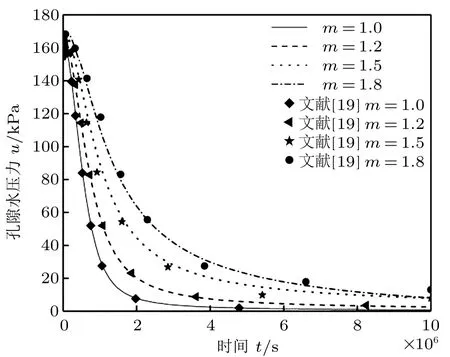
图2 本文计算结果与文献[19] 对比
文献[19] 采用有限体积法计算了Hansbo 渗流条件下基于UH 本构模型的饱和黏土一维固结问题,可以用来检验文中计算方法的可靠性。与文献对应的计算参数如下:在外荷载qt保持不变的前提下,Hansbo 渗流模型参数分别取:m=1.0(Darcy 渗流),1.2,1.5,1.8;i1取5.0;MG=1.5;H =5.0;E0=1.3;R0=0.5。UH 模型相关参数为:Cc=0.40;Ck=0.80;Cs=0.08;Cα=0.03;K0=3.0×10-7,其中,单位时间T0= 1。随着时间增加,孔隙水压力变化曲线如图2 所示。由图可知,与文献[19] 结果相比,本文计算方法及结果吻合比较好,说明文中数值模拟方法有较高的可靠度。
3 基于循环荷载的黏土固结特性分析
基于UH 本构模型和Hansbo 渗流且考虑循环荷载作用下的饱和黏土一维固结变形,影响变形固结过程的因素除了循环荷载的形式、周期、总循环周次等,UH 模型参数和Hansbo 渗流参数在变形固结过程中也有较大的影响。本文将分别进行模拟分析上述几种因素的影响。
图3(a)~图3(c) 为几种典型循环荷载形式,为便于分析计算,设Tc为无量纲周期,峰值qmax取100 kPa,q0= 10 kPa。同时,为对比分析结果,图3(d)给出了一个线性荷载的形式。Hansbo 渗流参数m= 1.6,i1= 5.0,土层厚度为1.0 m,其余参数同上。


图3 几种典型的循环荷载形式及线性荷载
3.1 循环荷载的影响
以图3 所示的几种典型循环荷载为例,为分析荷载形式的影响,对于非线性循环荷载,取Tc=2000;线性荷载Tc= 12 000。为便于对比分析,荷载取12个完整的循环周期,计算结果如图4~图6 所示。
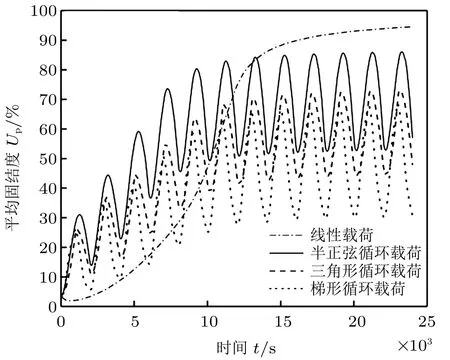
图4 荷载形式不同时平均固结度Up 随时间t 的变化曲线

图5 荷载形式不同时孔隙水压力u 随时间t 的变化曲线

图6 荷载形式不同时沉降量s 随时间t 的变化曲线
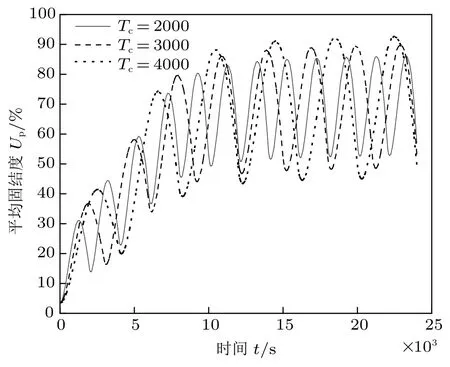
图7 周期不同时平均固结度Up 随时间t 的变化曲线
图4~图6 分别为荷载形式不同时平均固结度Up、超孔隙水压力u和沉降量s随时间t的增加而变化的曲线。可以明显看出,饱和黏土的平均固结度Up、超孔隙水压力u 和沉降量s 在周期性循环荷载作用下均呈现出周期性变化特征,同时在荷载循环过程中,孔隙水压力会出现负值。相同循环周次内,半正弦循环荷载作用下的平均固结度要大于梯形循环荷载和三角形循环荷载作用下的峰值,而且三角形循环荷载与梯形循环荷载加载形式对平均固结度变化特征及波峰值差值不大,但是梯形循环荷载固结度波谷值远低于三角形循环荷载波谷值。在多个循环周次,随着时间的增长,每个循环周次Up呈逐渐增大趋势,u 的峰值呈逐渐减小趋势;随着循环次数的增加,Up和u 基本进入稳定循环状态。同时,三种循环荷载作用下黏土达到稳定时的固结度峰值均小于线性荷载;线性荷载最终孔压趋近于0,循环荷载孔压在0 值附近稳定循环。
由图6 可知,相同的循环周次内,半正弦循环荷载作用下,地基沉降量峰值大于三角形循环荷载和梯形循环荷载作用下的沉降量峰值,随着循环周次的增加,地基沉降量趋于稳定循环状态;当达到稳定循环状态时,在恒定荷载作用下的地基沉降量大于循环荷载作用下的地基沉降量。
此外,以半正弦循环荷载为例,各参数同上述情况。由图7 和图8 表明,不同周期Up的震荡幅度随着周期Tc的增大逐渐增大,u 的震荡幅度随着周期Tc的增大逐渐减小。同一周次内平均固结度的峰值(波峰值和波谷值) 也随着周期的增大而增大,周次内超孔隙水压力的峰值绝对值(波峰值和波谷值)也随之减小,循环荷载周期越大,固结度峰值越大,孔压消散速率越快,固结速率越快。

图8 周期不同时孔隙水压力u 随时间t 的变化曲线

图9 周期不同时沉降量s 随时间t 的变化曲线
由图9 可以看出,固结初始阶段在同一个循环周期内,沉降量s 的峰值随着周期增大而增大,随着循环周次的增加,沉降量s 逐渐趋于稳定循环状态,达到稳定循环状态时,地基沉降量峰值则与循环荷载周期无关。
3.2 Hansbo 渗流参数的影响
以图3(a)所示的三角形循环荷载为例,取Tc=2000。Hansbo 渗流参数m 分别取1.0 (Darcy 渗流),1.5,2.0 和3.0(i1取5.0),i1分别取1.0,5.0,10.0和15.0 (m 取1.5),计算结果如图10 和图11 所示。

图10 m 不同时平均固结度Up 随时间t 的变化曲线

图11 m 不同时超孔隙水压力u 随时间t 的变化曲线
图10~图12 分别为Hansbo 渗流参数m 不同时平均固结度Up、超孔隙水压力u 和沉降量s 随时间的变化曲线。由图10 和图11 可知,平均固结度Up和超孔隙水压力u 在周期性循环荷载作用下均呈现出周期性循环变化特征。在前几个循环周期,每个周期内平均固结度Up的峰值呈逐渐增大趋势;每个周期内超孔隙水压力u 的峰值呈逐渐减小趋势,当循环周次较高时,平均固结度Up和超孔隙水压力u基本进入稳定循环状态。
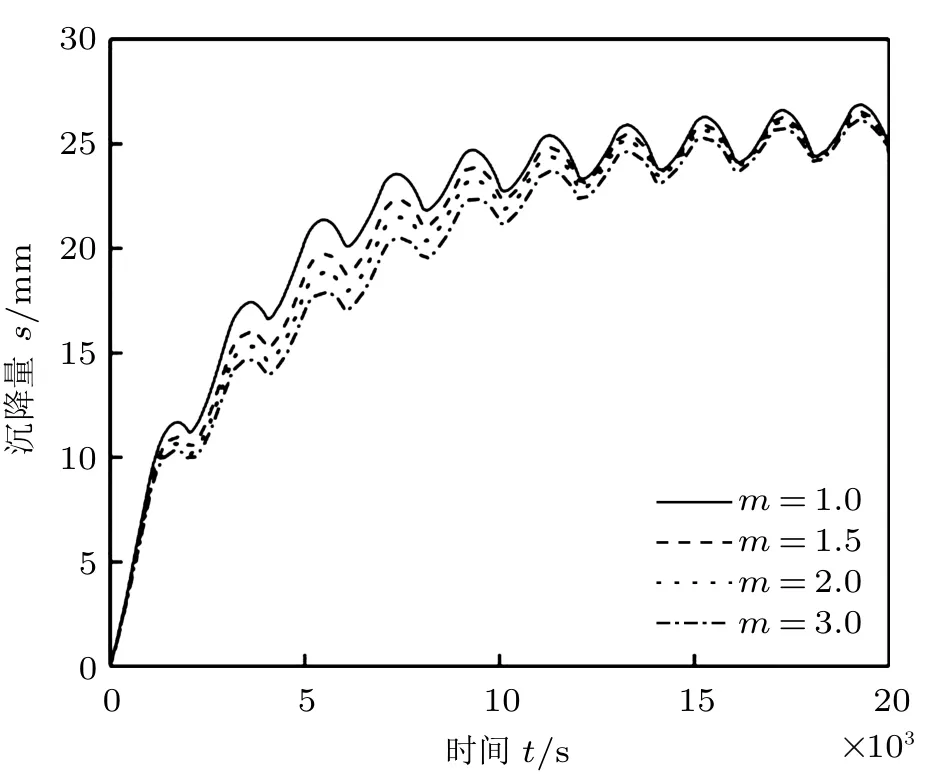
图12 m 不同时沉降量s 随时间t 的变化曲线
另一方面,随着参数m 的逐渐增大,地基土体中孔隙水的渗流越来越困难,导致变形速率也逐渐降低,因此,平均固结度Up和超孔隙水压力u 的波峰值及波谷值在同一循环周期内也随之降低,但是超孔隙水压力u 的变化幅度在同一循环周期内的改变不大。同时,参数m 对固结度和孔压的影响在中期较为明显,固结后期基本趋于同一循环。
由图12 可知,在相同的循环周次内,沉降量s的峰值随着m 值的增大而减小,在固结中期影响非常明显。随着循环周次的增加,沉降量逐渐趋于同一峰值。
图13 ~图15 分别为Hansbo 渗流参数i1不同时,随时间的增长,平均固结度Up、超孔隙水压力u和沉降量s 的变化曲线。同一循环周期内平均固结度Up的峰值随着参数i1的增大有明显的降低,且其同一周次内的变化幅度也有一定程度的降低。渗流参数i1对孔隙水压力u 的影响主要在固结中期较为明显,固结中期同一循环周次内孔压u 的峰值随着参数i1的增大逐渐增大,固结后期,逐渐趋于同一稳定循环。由图15 可知,在相同的循环周次内,沉降量s 的峰值随着i1值的增大而减小,在固结中期影响非常明显。随着循环周次的增加,沉降量逐渐趋于同一峰值。
由图10 ~图15 对比分析可知,Hansbo 渗流参数对固结的影响集中在中后期,随着m 和i1的增大,地基的沉降量逐渐减小,当固结完成时,地基最终沉降量与Hansbo 渗流参数无关。说明Hansbo 渗流参数只是在渗流固结的过程中有影响,对最终的结果没有影响。

图13 i1 不同时平均固结度Up 随时间t 的变化曲线
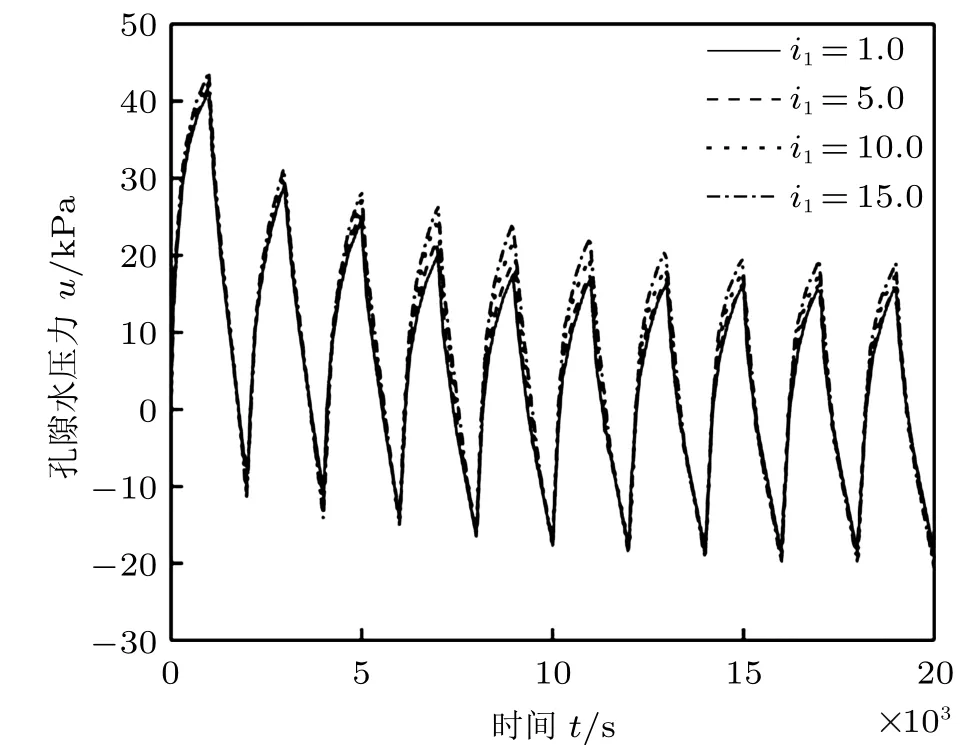
图14 i1 不同时超孔隙水压力u 随时间t 的变化曲线

图15 i1 不同时沉降量s 随时间t 的变化曲线
3.3 UH 模型参数影响
为分析UH 模型参数对平均固结度和土体中超孔隙水压力的影响,循环荷载与3.2 节相同,在UH模型参数中,土的压缩指数取0.021 7,e0取0.53。令土的次固结系数Cα分别取0,0.005,0.009 和0.013;土的回弹指数Cs分别取0.005,0.01 和0.02;渗透指数Ck分别取0.2,0.5 和0.8;初始超固结参数R0分别取0.25,0.55 和0.95。
图16 ~图18 分别为土的次固结系数Cα不同时,平均固结度Up、超孔隙水压力u 和沉降量s 随时间的变化曲线。由图16 可知,同一循环周次内平均固结度Up的峰值与Cα呈负相关关系,孔隙水压力u 的峰值与Cα呈正相关关系,沉降量s 的峰值随着Cα的增大逐渐增大。此外,Cα的变化对平均固结度Up和沉降量s 的影响非常显著,随着循环次数的增加,Up和s 将进入稳定循环状态,次固结系数越大,地基最终沉降量越大;而随着Cα的逐渐增大,同一循环周次内u 的峰值显著降低,最终在0 附近稳定循环。因此,次固结系数对饱和黏土地基固结影响非常明显,随着次固结系数的增大,孔隙水压力消散速率减慢,这种影响随次固结系数的增大越来越明显。
图19 ~图21 分别为UH 模型参数Cs不同时,平均固结度Up、孔隙水压力u 和沉降量s 随时间的变化曲线。由图可知,Cs的变化对平均固结度Up和孔隙水压力u 都有明显的影响:同一循环周次内u 的峰值随着Cs的增大而增大、Up的峰值随着Cs的增大而减小、沉降量s 的峰值随着Cs的增大而逐渐增大;参数Cs的值较小时,对沉降量s 的影响不明显,土体经过几个循环周次后就进入稳定循环状态。同时,在固结前期,Cs对孔隙水压力影响不明显,从中期开始产生明显影响,这与文献[19] 的结论类似。

图16 Cα 不同时平均固结度Up 随时间t 的变化曲线

图17 Cα 不同时孔隙水压力u 随时间t 的变化曲线
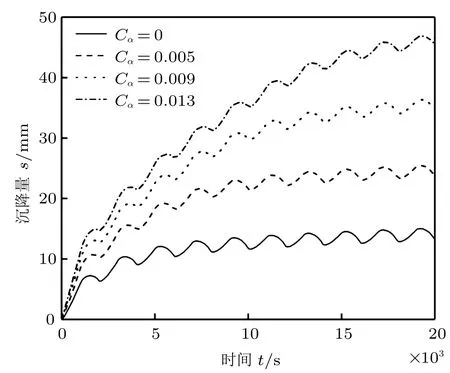
图18 Cα 不同时沉降量s 随时间t 的变化曲线

图20 Cs 不同时孔隙水压力u 随时间t 的变化曲线

图21 Cs 不同时沉降量s 随时间t 的变化曲线
图22~图24 分别为UH 模型参数Ck不同时,平均固结度Up、孔隙水压力u 和沉降量s 随时间的变化曲线。由图可知,Ck的变化对平均固结度Up、孔隙水压力u 和沉降量s 都有影响:Up的峰值在同一循环周次内随着Ck的增大而逐渐增大;u 的峰值随着Ck的增大而逐渐减小;沉降量s 的峰值随着Ck的增大而逐渐增大;土体经过几个循环周次后进入稳定循环状态。同时,Ck对Up,u 和s 的影响在固结过程前中期尤为明显,后期影响效果逐渐减弱,这与文献[19] 的结论类似。

图22 Ck 不同时平均固结度Up 随时间t 的变化曲线

图23 Ck 不同时孔隙水压力u 随时间t 的变化曲线
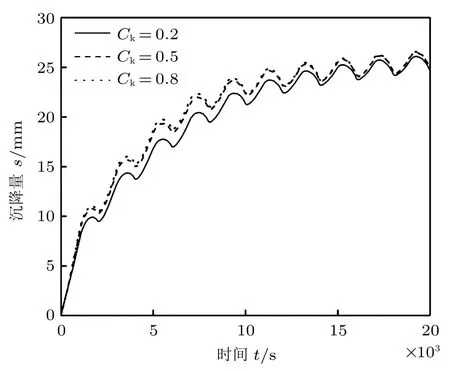
图24 Ck 不同时沉降量s 随时间t 的变化曲线
图25~图27 分别为UH 模型参数R0不同时,平均固结度Up、超孔隙水压力u 和沉降量s 随时间的变化曲线。R0的变化对平均固结度Up、孔隙水压力u和沉降量s都有比较明显影响:同一循环周期内Up的峰值与R0呈负相关关系;u的峰值与R0呈正相关关系,沉降量s的峰值随着R0的增大逐渐增大。且R0越大,这种变化趋势越明显,在固结过程的前期,R0对固结影响程度较大。R0对固结最终沉降量影响非常明显,R0越大,地基最终沉降量越大。

图25 R0 不同时平均固结度Up 随时间t 的变化曲线
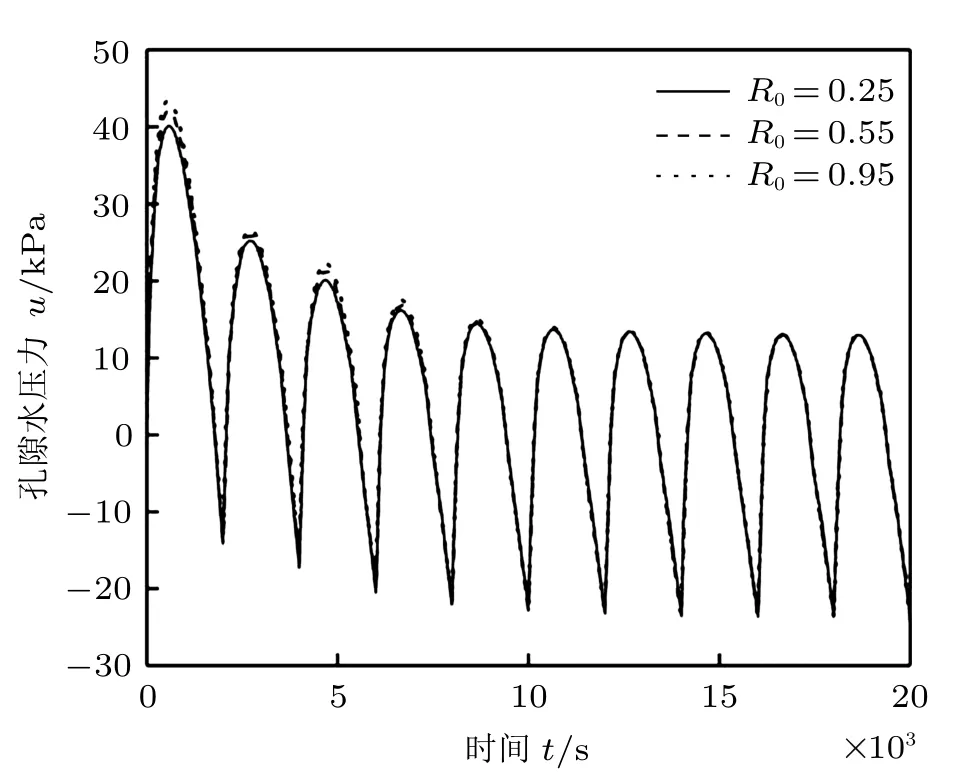
图26 R0 不同时孔隙水压力u 随时间t 的变化曲线

图27 R0 不同时沉降量s 随时间t 的变化曲线
4 结论
本文在考虑Hansbo 渗流模型和UH 模型的基础上,通过在传统的一维固结理论中引入UH 模型应变关系和Hansbo 渗流规律,从而推导了循环荷载作用下以超孔压u和竖向应变εv为变量的黏土一维固结方程,在该固结方程进行数值分析计算中采用FlexPDE 软件,在此方法基础上,研究了饱和黏土在周期性循环荷载作用下的一维固结特性,分析了荷载类型和周期、Hansbo 渗流参数以及UH 模型参数对黏土固结特性的影响。主要结论如下:
(1) 在研究土体固结变形问题时,采用超孔压u和竖向应变εv描述的饱和软黏土一维固结方程,能够很好地求解。
(2) 地基平均固结度Up、超孔隙水压力u和沉降量s在循环荷载作用下均呈现循环变化特征。在荷载作用下,当循环周次较高时,u的值基本围绕在0 附近,进入稳定循环状态。
(3)半正弦循环荷载作用下的平均固结度Up、超孔隙水压力u和沉降量s的波峰值要大于梯形循环荷载和三角形循环荷载作用下的波峰值,三角形循环荷载和梯形循环荷载加载形式对平均固结度、超孔隙水压力和沉降量变化特征及波峰值影响小于波谷值,循环荷载作用下的固结度达到稳定循环后均小于线性荷载作用下的固结度。
(4) 地基固结速率与Hansbo 渗流参数m和i1之间存在负相关关系,当m和i1增大时,同一循环周次内Up的峰值减小,在固结前期和末期其变化幅度受m影响小,随着i1增大在固结中期有小幅度的降低。
(5) 在同一循环周次,Up的峰值与次固结系数Cα存在负相关关系,而u的峰值与次固结系数Cα存在正相关关系,且u的峰值随着循环周次的增加缓慢降低。随着土的回弹指数Cs逐渐增大,同一循环周次内Up的波峰值逐渐减小,波谷值逐渐增大,孔压u的波峰值逐渐增大,波谷值逐渐减小,沉降量s的峰值增大非常明显;但是相对于次固结系数,回弹指数的影响程度相对较小。当渗透指数Ck逐渐增大时,同一循环周次内Up的峰值逐渐增大;u的峰值逐渐减小,沉降量s的峰值逐渐增大,且在固结后期影响较为微弱。随着初始超固结参数R0的逐渐增大,同一循环时间内Up的峰值逐渐减小;u的峰值逐渐增大;沉降量s的峰值逐渐增大,且R0在固结前中期影响较明显,固结后期趋近于同一稳定循环。
(6)地基的平均固结度在周期性循环荷载作用下始终处于循环状态,固结度曲线随着时间的增长将达到稳定循环状态。

