基于高精度MEMS-INS的双轴旋转调制技术*

王思远,刘海桥,罗世彬

(1.中南大学 航空航天学院,湖南 长沙 410086;2.中南大学 自动化学院,湖南 长沙 410086)

0 引 言

由于具有高精度,高自主性,抗干扰性强的优势,捷联惯性导航系统(strapdown inertial navigation system,SINS)已成为导航系统不可分割的一部分[1]。然而,SINS的缺陷是误差随时间迅速累积,SINS的主要误差是惯性传感器误差,惯性传感器[2～4]精度限制着惯性导航系统(INS)的精度。旋转调制技术可用于消除惯性传感器常值漂移的影响,在光学陀螺惯性导航系统中的应用已比较成熟,但在微机电系统(MEMS)-INS上的应用研究较少,且缺少系统分析。针对MEMS惯性器件常值零偏误差、标度因数误差、标度因数对称性误差较大且不稳定的特点,需要选择更合适的旋转方法,通过对比不同旋转方法的误差补偿效果,可以确定适用于MEMS-INS的旋转方案。

1 旋转调制技术

旋转调制技术通过对惯性测量单元(inertial measurement unit,IMU)进行周期性的旋转来实现惯性传感器的常值误差进行补偿。

1.1 坐标系定义

1)惯性坐标系(i系)的原点为地球中心,x，y轴处于赤道平面内,x轴指向春分点,z轴为地球自转轴,并指向北极,y轴由右手定则获得。2)地球(e系)坐标系的原点为地球中心,x，y轴处于赤道平面内,x轴指向春分点,z轴为地球自转轴,并指向北极,y轴由右手定则获取。地球坐标系与地球固连,随着地球自转。3)载体坐标系(b系)的原点在载体中心,x轴指向车辆或载体的右方,与俯仰轴重合,y轴指向载体的正前方,与横滚轴重合,z轴指向载体的上方,与载体的航向轴重合。4)当地理坐标系(t系)的原点为载体坐标系的原点在大地水平面上的投影,x轴指向地理东向,y轴指向地理北向,z轴指向天向。5)本文中导航坐标系(n系)选取为当地地理坐标系。

1.2 旋转调制消除误差的基本原理

在捷联算法中,惯性导航系统误差传播方程如下[5]

(1)

1.3 旋转调制的基本方法

旋转调制方案的设计需要确定转轴个数、旋转角速度、停止时间、转停位置。

1)转轴个数:转轴个数可分为单轴、双轴及多轴。其中单轴旋转的优点为结构简单,但无法补偿沿转轴方向传感器的常值误差,造成惯性导航系统精度较低。双轴及多轴旋转调制的优点为可以补偿掉三个轴向惯性传感器的常值误差,但结构复杂,故障概率高。高精度INS大多采用双轴或多轴旋转方式。

2)旋转角速度:当IMU绕Z轴以角速度ω转动时,对东向以及北向常值漂移在任意两个时间段内积分可得式(2)[6],由式(2)可以看出,IMU转动时的误差角度积累与转动角速度成反比,即转动角速度越大,转动周期越短,对常值漂移误差补偿的越完全。式(2)如下

(2)

3)停止时间:高精度INS大多数采取不连续转停方法,转停方法的优点为电机负担较小,缺点为在停止位置时误差发散较快,连续旋转方案优点为持续旋转,可以将常值误差连续补偿,缺点为电机负担较大,造成电机寿命短。具体停止时间的选择由惯性传感器的误差分析确定[7～9]。

2 MEMS-INS及其误差特性

由于MEMS-INS的常值零偏误差、标度因数误差和标度因数对称性误差大,MEMS-INS在高精度应用中非常有限。为了补偿上述误差,可以使用旋转调制技术。但大部分旋转调制技术应用于单轴。东南大学用Kalman滤波对INS误差进行了估计[10]。在文献[11]中,基于单轴旋转调制设计了参数标定方法和补偿方法来补偿旋转轴向的误差。

MEMS惯性传感器误差主要包括常值零偏误差,零偏稳定性,热机械白噪声,温度影响以及标定误差(包括标度因数、线性度)。对于MEMS惯性传感器,在温度的影响下,上述误差及其重复性很差。由于确定性误差占据了误差的大部分,对其进行补偿十分有必要。

3 旋转调制方法分析与设计

3.1 单轴360°往复旋转

在文献[12]中,选用了基于MEMS-INS的单轴360°往复旋转方法,具体旋转步骤如图1所示。由于旋转调制技术中陀螺仪与加速度计的误差模型相同,故仅以陀螺仪为例分析误差调制效果,验证是否会在一个完整周期的转位运动内造成误差累积。

(3)

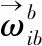
陀螺的标度因数误差矩阵定义为

(4)

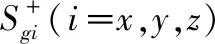
陀螺的标度因数对称性误差矩阵定义为

(5)

由上可得,数学平台的误差角速度为

(6)

将每次转动的初始时间设置为0,每个步骤旋转的旋转矩阵如图1所示。

图1 单轴两位置旋转步骤示意

一个完整旋转周期内常值零偏误差的误差角度积累为

(7)

在一个转动周期内标度因数误差角度积累为

(8)

在一个旋转周期内标度因数对称性误差积累的角度误差为

(9)

由上可得,单轴两位置往复运动可以完全补偿掉标定因数误差,但常值零偏误差及标度因数对称性误差不能完全补偿。

3.2 双轴十六位置连续转动方法设计与分析

旋转调制方案的转轴数量分为单轴、双轴以及多轴,由于单轴旋转无法补偿旋转轴方向的误差,双轴以及多轴旋转可以补偿3个轴向的常值误差,因此本文选用了双轴十六位置连续旋转方法。具体旋转步骤如图2所示。

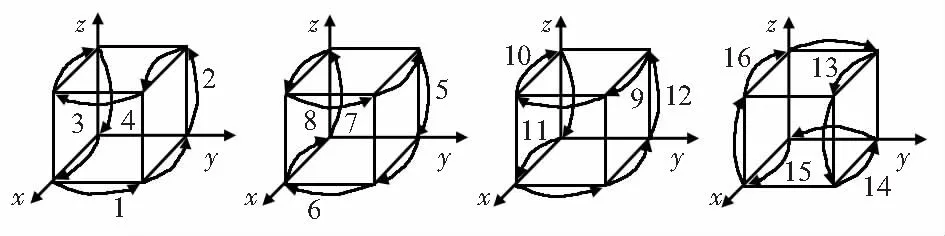
图2 双轴十六位置旋转步骤示意

与单轴两位置往复旋转相同,将每次转动的初始时间设置为0。

一个完整旋转周期内常值零偏误差的误差角度积累为

(10)

一个转动周期内标度因数及标度因数对称性误差积累为

(11)

由上可得,双轴十六位置连续旋转可以补偿上述全部误差,相比于单轴两位置,双轴十六位置连续旋转可以完全补偿掉常值零偏误差及标度因数对称性误差。

4 仿真结果与分析

将上述误差进行仿真,仿真时长为720 s,采样时长0.001 s,陀螺常值零偏为2°/h,加速度计常值零偏为1 mgn,标度因数误差为100×10-6,标度因数对称性误差为20×10-6,仿真结果如图3所示。

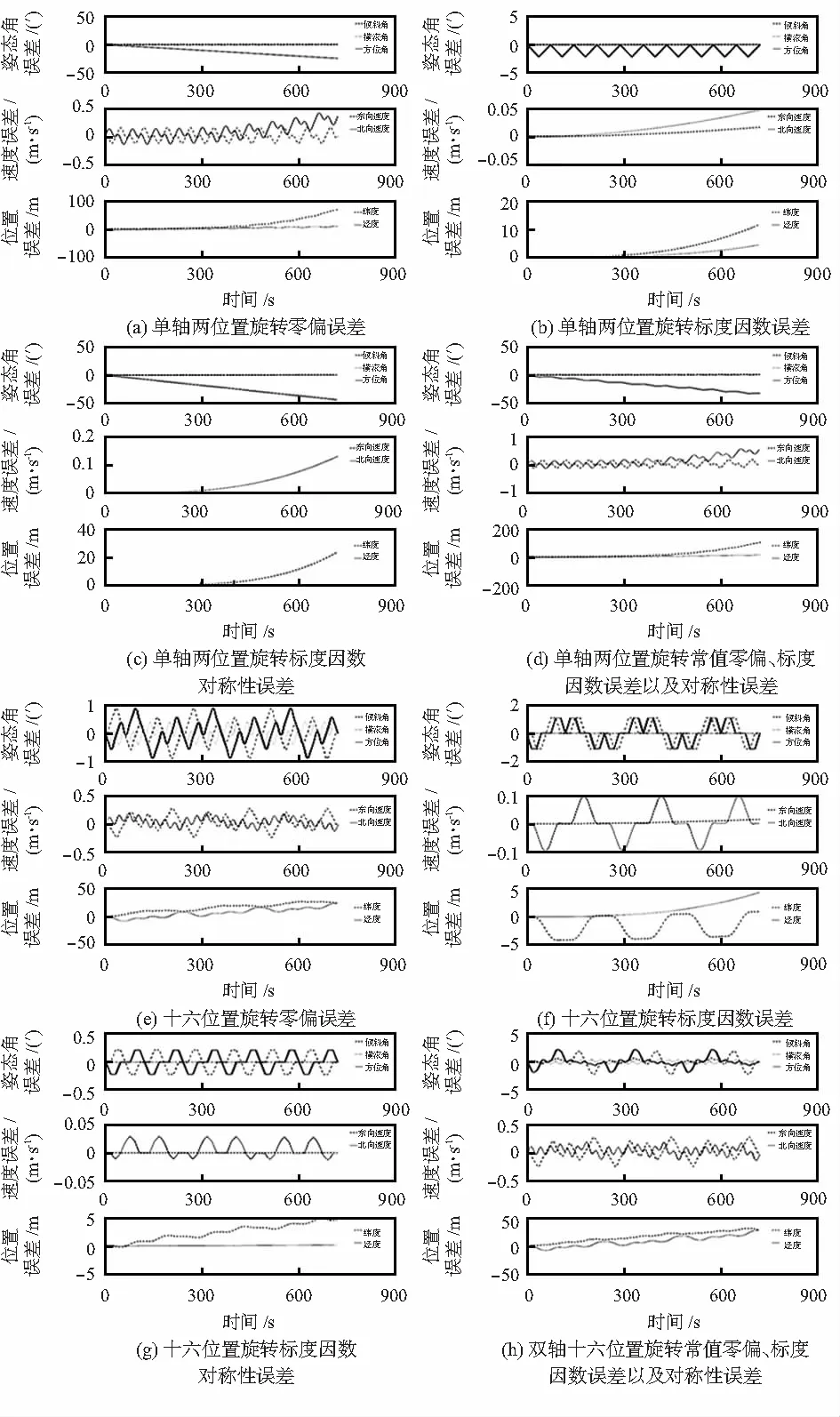
图3 仿真结果

由表1得出,在注入三种误差条件下俯仰角误差由0.75减小为0.015,横滚角误差,由0.018 m/s减小为0.002 m/s,航向角误差由32.63减小为0.001,东向速度误差由0.02 m/s减小为0.011 m/s,北向速度误差由0.54 m/s减小为0.021 m/s,东向位置误差由105.6 m减小为29.6 m。故可判断双轴十六位置旋转很好地补偿了MEMS陀螺仪与加速度计的常值零偏误差以及标度因数对称性误差。

表1 上述三种误差情况下两种旋转导航误差对比

5 结 论

仿真结果表明,相对于单轴两位置旋转方案,双轴十六位置旋转方案具有更好的调制效果,720 s内速度精度提高了2倍,位置精度提高了近3倍。