微尺度MEMS 上层芯片表面应变测量的方法研究

罗钧文，戴 强，陈 翔

（西南科技大学制造过程测试技术省部共建教育部重点实验室，四川 绵阳 621010）

1 引言

MEMS 封装结构中各层材料间的热膨胀系数不匹配，造成整个MEMS 器件中存有残余应力以及封装结构的热变形，严重影响该器件在高性能要求场合的使用[1]。因此，测量MEMS 结构中的应变成为了研究关键。近年来，关于微尺度结构应变的测量，国内外的研究人员做了大量的研究和实验。云纹法、散斑法和网格法等传统测量表面应变方法只能测量较大尺寸应变；参考文献[2-6]利用SEM 和数字图像相关方法技术来测量微米级甚至是亚微米级的表面变形，都只能是测量一个SEM 镜头视野中的应变。

根据应变的定义ε=△L/L，在以上的研究中，L 取值最大只能是一个镜头视野的长度（100μm～200μm），而△L 的数值一般是微米或亚微米级（100nm～10μm），导致测量到的应变数值也较大（10-3～10-1数量级），无法满足MEMS 结构中微小应变的测量要求。为了改善上述方法中微尺度测量应变方法的缺点，提出了一种采用光刻方法来标记L，基于光学显微视觉来获得△L，从而测得MEMS 结构中微小应变的方法。

2 测量方法

实验采用SEMISHARE 探针台，如图1 所示。探针台配备有加热台、光学显微镜和CCD 相机。采用以上设备获得有光刻图案芯片的数字图像。

图1 实验采用的SEMISHARE 探针台Fig.1 Probe Station of SEMISHARE for Experiment

为获得较大的L，本研究采用在硅片上光刻图案的方法。实验采用的试件为N 型晶向（100）硅片，划片后的裸片面积尺寸为（15×15）mm，其表面设计（10×10）μm 的正方形特征图案，并采用光刻工艺加工，每个图形之间的间隔为3μm；采用从左至右，从下至上依次在每隔200μm 左右做一个数字标记，如图2 所示。

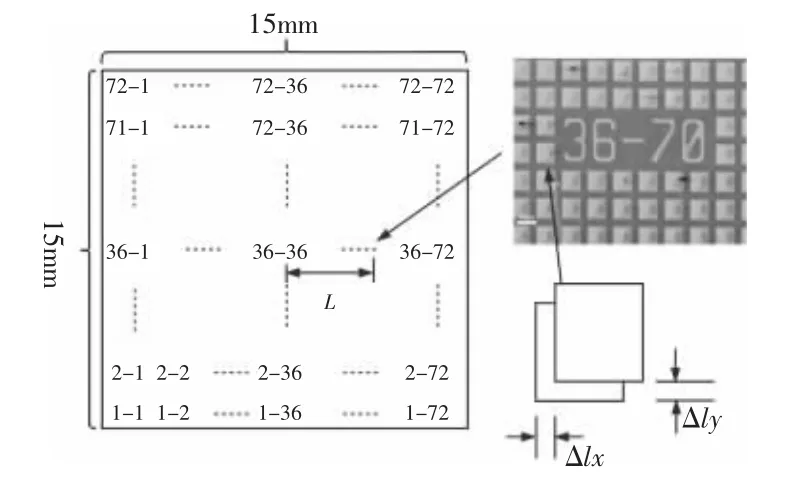
图2 测量原理图Fig.2 Schematic Diagram of Measurement

以采集到的36-70 区域图像为例，如图2 所示。取其中一个方格边缘为特征，得到其在变形前后沿x、y 方向的位移距离为△Lx和△Lv，计算得到表面变形前后的位移距离为△L；36-36 区域和36-70 区域之间在变形前的距离长度为L，可根据设计的版图知道。两区域间变形前后的伸长量可表示为：

基于图1 所示设备，利用MATLAB 软件编程对图像进行预处理和图像边缘特征提取，来计算两区域之间在变形后的伸长量△L。下面简单介绍处理步骤：

（1）基于二维伽马函数的光照不均匀图像自适应校正算法[7]，使采集的图像光照均匀，改善图像的质量；

（2）采用3×3 的均值滤波，取领域内的像素灰度值作为当前像素的灰度值，对图像进行平滑、去噪；

（3）对处理过的图像进行灰度化，采用Otsu 大津算法，自适应的确定阈值为124，得到二值化图像。

（4）利用Canny 算子提取出边缘特征，在进行细化处理得到单像素值的边缘。Canny 算子的基本思想是：先对图像进行高斯滤波，再对像素点进行非极大值抑制，运用双阈值法将小于阈值的所有值都赋予为零，得到的高阈值边缘图像连接成边缘轮廓。

（5）图像形态学处理。对图像进行细化处理，得到单像素值边缘。

以数字标记36-36 区域图像为例，进行上述一系列图像处理步骤，如图3 所示。

图3 MATLAB 数字图像处理的结果Fig.3 The Results of MATLAB Digital Image Processing

数字图像处理得到的表示的是像素值。经过系统标定后，得到了图像像素尺寸与实际物理空间尺寸的对应关系，即每个像素对应的实际尺寸为0.25μm。

通过以上方法，分别得到实际尺寸的L 与△L，根据应变公式，即可得到硅片试样的应变。

3 实验结果与讨论

为验证以上测量方法，将试件放在探针台上加热，通过测量硅片的热膨胀系数值来验证这种测量方法的可行性，如图2 所示。

在实际的实验测量中，材料的热膨胀系数的表达式为：

式中：α—在一定温度间隔△T 的平均线热膨胀率；△L—在温度变化△T 内的材料线性热膨胀量；L—变形前的长度。

选取试件表面标记的36-36 区域和36-70 区域，进行20℃至100℃的加热，经过8 组实验的测量，如表1 所示。

表1 36-36 和36-70 区域图像的相对像素位移差值Tab.1 Relative Pixel Displacement Difference of the 36-36 and the 36-70 Area Images

得到两区域的平均相对像素位移为：

得到实际尺寸与像素值的关系为：

根据设计的版图尺寸，得到两参考直线间的距离为：

可得硅芯片热膨胀系数在温度变化△T=80℃内的实际测量平均值为：

参照上述测量硅片的热膨胀系数值的方法，随机在试件表面选取了5 个点，如图4 所示。标记了5 条测量路径，在20℃加热至100℃（△T=80℃）的相同实验条件下，每条测量路径经过多次实验取平均值，得到每条测量路径的热膨胀系数实验值。

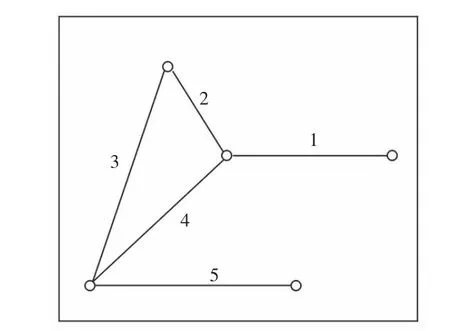
图4 试件表面选取的5 条测量路径示意图Fig.4 Schematic Diagram of Five Measuring Paths Selected on the Surface of the Specimen

对于硅片的热膨胀系数的理论值，根据相关文献[8-12]。取理论值为3.0（T=373.15K），可得出热膨胀系数实验值和理论值的关系，如图5 所示。

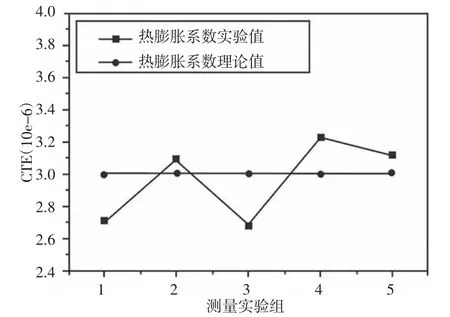
图5 不同测量路径下的热膨胀系数实验值与理论值对比Fig.5 Comparison of Experimental Values and Theoretical Values of the Thermal Expansion Coefficient of Different Measurement Paths

结果表明：实际测量值在理论值上下的一定范围内波动，最小的相对误差为3%，最大的相对误差为10.67%，实验的误差范围基本在10%以内。

针对微米级的图像采集，在现有实验条件下，因为加热台和精密光学隔振平台的细微振动都可能造成有一两个像素的误差，这是在光学显微系统中不能完全避免的外界干扰因素。

设置温度对照实验。在20℃至120℃的温度范围内，每间隔25℃采集测量一次热膨胀系数实验值，在20℃、45℃、70℃、95℃、120℃的温度下多次实验测量得到热膨胀系数实验值，每个温度下测量的实验组取平均值，与理论值作比较，绘制如图6 所示。

图6 不同温度下热膨胀系数实验值与理论值对比Fig.6 Comparison of Experimental Values and Theoretical Values of the Thermal Expansion Coefficient at Different Temperatures

由图可见：在20℃至120℃的温度范围内，硅芯片的热膨胀系数随温度的升高而增大。同时，实验值与理论值的曲线较为接近，它们的平均相对误差在8%左右，是在比较小且可靠的一个误差范围内，两者的数值比较吻合。在整个温度升高的过程中，实验值都比理论值偏大。在45℃时，热膨胀系数实验值在整个增长趋势中偏小，呈现出不一样的趋势，考虑到实验过程刚开始的阶段，测量平台处于在加热的初始阶段，实验平台还处于受热不均，因此出现实验测量的热膨胀系数值偏小。同时，在90℃以下的温度，实验值的数值增大速率比较快；在90℃之后，热膨胀系数实验值增大速率变得缓慢且较为接近理论值。我们可以预测，在120℃以上的温度，实验值的增大速率趋于缓慢，增大趋势逐渐与理论值的增大趋势，与理论值越来越接近。

4 结论

提出了一种结合了光学显微系统、微光刻工艺和数字图像处理技术的微尺度硅芯片表面应变测量方法。通过验证硅芯片表面的热膨胀系数的实验值与理论值平均相对误差在10%以内，表明此实验方法可成功应用于MEMS 上层芯片表面应变的测量。