两个保序全变换半群的直积上的主同余
尚传翠,杨秀良
(杭州师范大学理学院,浙江 杭州 311121)
0 引言

为了叙述清楚结果,需要下面符号和术语.

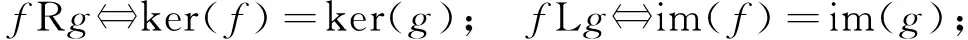


设A,B为非空集,且C⊆A×B,C≠∅,C的第一投影π1、第二投影π2分别定义为:
π1(C)={i∈A|∃j∈B,使得(i,j)∈C};π2(C)={j∈B|∃i∈A,使得(i,j)∈C}.
本文的主要结果如下:








□
1 主要结果的证明








(f,g)θ(f,g′)⟹(f′,g)=(h,1)(f,g)(h′,1)θ(h,1)(f,g′)(h′,1)=(f′,g′),
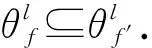
□
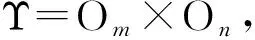
证明显然,有限多个Ii×Ij形式的集合的并是Υ的理想.


(1)如果θ有一个等价类A使|π1(A)|≥2,|π2(A)|≥2,则θ有一个等价类为Υ的理想;
(2)θ最多有一个等价类为理想.


下证I1×I1含于θ的一个等价类.

(Ca,Ce)θ(Ca,Cb),(Cd,Ce)θ(Ca,Ce)⟹(Ca,Cb)θ(Cd,Ce),
所以I1×I1含于θ的一个等价类[(Ca,Cb)]θ中.
任取(x,y)∈[(Ca,Cb)]θ,(x′,y′)∈Υ,则有
(xx′,yy′)θ(Cax′,Cby′)∈I1×I1⊆[(Ca,Cb)]θ.
进而(xx′,yy′)∈[(Ca,Cb)]θ,同理可证得(x′x,y′y)∈[(Ca,Cb)]θ,故[(Ca,Cb)]θ是Υ的一个理想.
(2)假设I,J为θ的两个不同的等价类,并且都是Υ的理想,则有IΥ⊆I,ΥJ⊆J.特别地,IJ⊆I,IJ⊆J.因此,IJ⊆I∩J,于是I∩J≠∅,这与I,J是θ的两个不同的等价类相矛盾,故而θ最多有一个等价类为理想.
□


假设|f|≤|f′|=j,因为f≠f′,所以im(f)≠im(f′)或ker(f)≠ker(f′),分别考虑这两种情况.
情况1 当im(f)≠im(f′)时,因为|f′|=j≥|f|,所以im(f)im(f′).又是正则的,则存在幂等元使得于是im(f)=im(h),且fh=f.所以
(f′h,g′)=(f′,g′)(h,1)θ(f,g)(h,1)=(fh,g)=(f,g)θ(f′,g′),
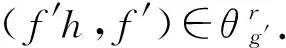
情况2 当ker(f)≠ker(f′)时,因为|f′|=j≥|f|,所以ker(f)ker(f′).同上存在幂等元使得于是ker(h)=ker(f).进而
(hf′,g′)=(h,1)(f′,g′)θ(h,1)(f,g)=(hf,g)=(f,g)θ(f′,g′),
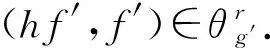
□
引理6设θ是由((f,g),(f′,g′))生成的主同余,且f=f′,g≠g′,k=max{|g|,|g′|},则(a,b)θ(c,d)当且仅当下列条件之一成立:
(1)(a,b)=(c,d),|a|>|f|或|b|>k;
(2)a=c,|a|≤|f|且max{|b|,|d|}≤k.

(1)(a,b)=(c,d),|a|>|f|或|b|>k;
(2)a=c,|a|≤|f|且max{|b|,|d|}≤k.
先证θ′是等价关系.自反性和对称性显然,下证传递性.设
((x,y),(x′,y′))∈θ′, ((x′,y′),(x″,y″))∈θ′.
如果(x,y),(x′,y′)满足条件(1),则(x,y)=(x′,y′),于是(x,y)=(x′,y′)θ′(x″,y″);如果(x,y),(x′,y′)满足条件(2),则x=x′,|x|≤|f|且max{|y|,|y′|}≤k.因为(x′,y′)θ′(x″,y″),故x′=x″,max{|y′|,|y″|}≤k,进而x′=x″,max{|y|,|y″|}≤k,所以(x,y)θ′(x″,y″).


((a,g),(a,g′))=((ufv,g),(ufv,g′))=((u,1)(f,g)(v,1),(u,1)(f,g′)(v,1))∈θ,

因此θ′⊆θ.
另一方面,因为(f,g),(f′,g′)满足条件(2),故((f,g),(f′,g′))∈θ′,于是θ⊆θ′.
□
类似于引理6,有以下引理.
引理7设θ是由((f,g),(f′,g′))生成的主同余,且f≠f′,g=g′,j=max{|f|,|f′|},则(a,b)θ(c,d) 当且仅当下列条件之一成立:
(1)(a,b)=(c,d),|a|>j或|b|>|g|;
(2)b=d,|b|≤|g|且max{|a|,|c|}≤j.
引理8设θ是由((f,g),(f′,g′))生成的主同余,且f≠f′,g≠g′,令|f|=i,|g|=j,|f′|=k,|g′|=l,则θ是由理想I=(Ii×Ij)∪(Ik×Il)决定的Rees同余.
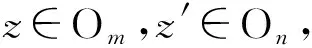
情况1 当k≤i,l≤j时,I=Ii×Ij.因为f≠f′,g≠g′,由引理4得,θ有一个等价类K为理想,下证(f,g)∈K.
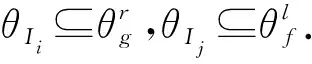
由于K是θ的一个等价类,因此(f′,g′)∈K.而I是包含{(f,g),(f′,g′)}的最小理想,故I⊆K,进而θI⊆θ.
相反地,因为θ是由((f,g),(f′,g′))生成的主同余,而((f,g),(f′,g′))∈θI,所以θ⊆θI,于是θ=θI.
情况2 当i≤k,j≥l时,I=(Ii×Ij)∪(Ik×Il).因为f≠f′,g≠g′,由引理4得,θ有一个等价类K为理想,下证(f,g)∈K.

(f,z′)θ(f,g)θ(f′,g′)θ(z,g′).

(f,g)θ(f,z′)=(fhf,z′)=(f,z′)(h,z′)(f,z′)θ(f,z′)(h,z′)(z,g′)=(z,z″)∈K,
于是(f,g)∈K.
因为K是θ的一个等价类,所以(f′,g′)∈K.而I是包含{(f,g),(f′,g′)}的最小理想,因此I⊆K.进而θI⊆θ.
相反地,因为θ是由((f,g),(f′,g′))生成的主同余,而((f,g),(f′,g′))∈θI,所以θ⊆θI,于是θ=θI.
综上,θ是由理想I=(Ii×Ij)∪(Ik×Il)决定的Rees同余.
□



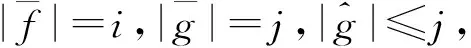


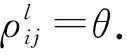






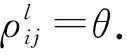

当(f,g)=(f′,g′)时, (fx,gy)=(f′x,g′y),于是((fx,gy),(f′x,g′y))∈σij;当(f,g)≠(f′,g′)时, |f|≤i,|g|≤j,|f′|≤i,|g′|≤j.因为
|fx|≤|f|≤i,|gy|≤|g|≤j,|f′x|≤|f′|≤i,|g′y|≤|g′|≤j,
故((fx,gy),(f′x,g′y))∈σij.
因此σij具有右兼容性,同理可证得σij具有左兼容性,进而σij是由I=Ii×Ij决定的一个Rees同余.


当(f,g)=(f′,g′)时, (fx,gy)=(f′x,g′y),于是((fx,gy),(f′x,g′y))∈σijkl; 当(f,g)≠(f′,g′)时,
(|f|,|g|),(|f′|,|g′|)∈({1,…,i}×{1,…,j})∪({1,…,k}×{1,…,l}).
因为|fx|≤|f|,|gy|≤|g|,|f′x|≤|f′|,|g′y|≤|g′|,故(fx,gy),(f′x,g′y)∈(Ii×Ij)∪(Ik×Il),于是((fx,gy),(f′x,g′y))∈σijkl.
因此σijkl具有右兼容性,同理可证得σijkl具有左兼容性,进而σijkl是由I=(Ii×Ij)∪(Ik×Il)决定的一个Rees同余.

□







C1 若θ为定理1中(1)的形式,则θ=δl;
C2 若θ为定理1中(2)的形式,则存在((a,b),(c,b))∈θ,使得|a|=|b|=|c|=1,a≠c.故((a,b),(c,b))∉δl,矛盾;
C3 若θ为定理1中(3)或(4)的形式,则存在((a,b),(c,d))∈θ,使得|a|=|b|=|c|=|d|=1,a≠c,b≠d.故((a,b),(c,d))∉δl,矛盾.


C1 若θ为定理1中(1)或(2)的形式,则θ=δl或θ=δr;
C2 若θ为定理1中(3)或(4)的形式,则任取((a,b),(c,d))∈δl,有
|a|=|b|=|c|=|d|=1, ((a,b)≠(c,d)).
进而((a,b),(c,b))∈I1×I1⊆θ,故θ不是极小同余.

□

