泡沫金属夹芯海洋工程管道冲击动态响应研究*
王贤贵 朱 凌 郭开岭 刘清扬
(武汉理工大学交通学院1) 武汉 430063) (武汉理工大学高性能舰船技术教育部重点实验室2) 武汉 430063)(高新船舶与深海开发装备协同创新中心3) 武汉 430063)
0 引 言
海洋油气运输管道经常会受到拖网渔具等重物的撞击,这种作用会使管道产生凹痕和横向弯曲,极端情况下甚至会使油气资源泄露,造成不可估量的财产损失和严重的环境污染,而这种损坏的修理代价是十分昂贵的.
泡沫金属作为一种典型的多孔材料,具有密度小、比吸能高等优点,其力学性能得到了细致研究[1-3].泡沫金属的抗拉、抗剪切能力较差,而与金属薄壁圆管组成的夹芯结构可以克服以上缺点,充分发挥泡沫金属芯层的能量吸收特性和优异的抗冲击能力,为油气运输和防撞防护等提供安全保障.Jones等[4]对钢圆管进行了系列冲击实验,探究了圆管受冲击载荷下的变形规律.Zhu等[5]在原有实验的基础上拓展了实验范围.提出通过上下表面变形的不同来区分圆管整体与局部变形模式的方法.刘清扬等[6]通过有限元计算验证了实验中提出的方法,并对圆管的局部变形大小拟合了经验公式描述.Li等[7]开展了单层管、填充管和夹芯管三种不同的管状结构的动态三点弯实验,根据能量吸收比和能量吸收因子评估了动态抗弯性能和能量吸收特性.Liu等[8]对泡沫铝夹芯管的抗爆炸冲击性能进行了有限元分析,结果表明泡沫铝夹芯管的径向变形和抗爆炸冲击能力都明显优于单层管.Jing等[9]对泡沫铝夹芯管在冲击载荷下的能量吸收能力和失效机理进行了实验分析.发现内壁的厚度较之外壁的作用更为重要.Liang等[10]通过实验和数值仿真方法,研究了泡沫铝夹芯管在内部爆炸载荷作用下的冲击响应,分析了管变形过程的三个阶段,即外管加速、芯层压实和内管变形.
目前对于泡沫金属夹芯管横向冲击动态响应的研究还较少,冲击失效机理尚不明确,阻碍了夹芯管的工程应用.文中利用实验和数值仿真方法,对泡沫金属夹芯管的横向冲击动态响应进行了研究.对比仿真与实验结果,验证数值方法的可靠性.在此基础之上,利用数值仿真技术研究了冲击能量、冲击位置对夹芯管冲击动态响应的影响规律.
1 有限元方法
1.1 材料参数
利用WDW-100万能试验机,进行不锈钢管材的准静态拉伸实验和泡沫金属的准静态压缩实验.泡沫金属压缩试样的尺寸为直径×长度=60 mm×40 mm,平均密度为0.496 g/cm3,弹性模量为157 MPa;不锈钢材料的密度为7.8 g/cm3,弹性模量为203 MPa,泊松比为0.3.材料的塑性应力-应变曲线见图1.
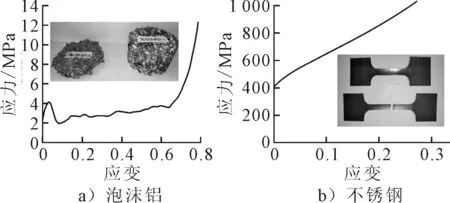
图1 材料的塑性应力-应变曲线
1.2 有限元模型
采用ABAQUS/Explicit模型建立夹芯管横向冲击有限元模型,模拟冲击动态响应过程.泡沫金属夹芯管模型尺寸与实验保持一致,长度为180 mm、外管直径为38 mm、厚0.8 mm,内管直径为19 mm、厚0.6 mm,芯层厚度8.5 mm,其横截面见图2.芯层采用可压碎泡沫模型,定义弹性模量和泊松比,输入塑性应力-应变关系(见图1a)),并定义极限屈服强度比和塑性泊松比.不锈钢管采用弹塑性模型,定义弹性模量和泊松比,输入塑性应力-应变关系,见图1b).
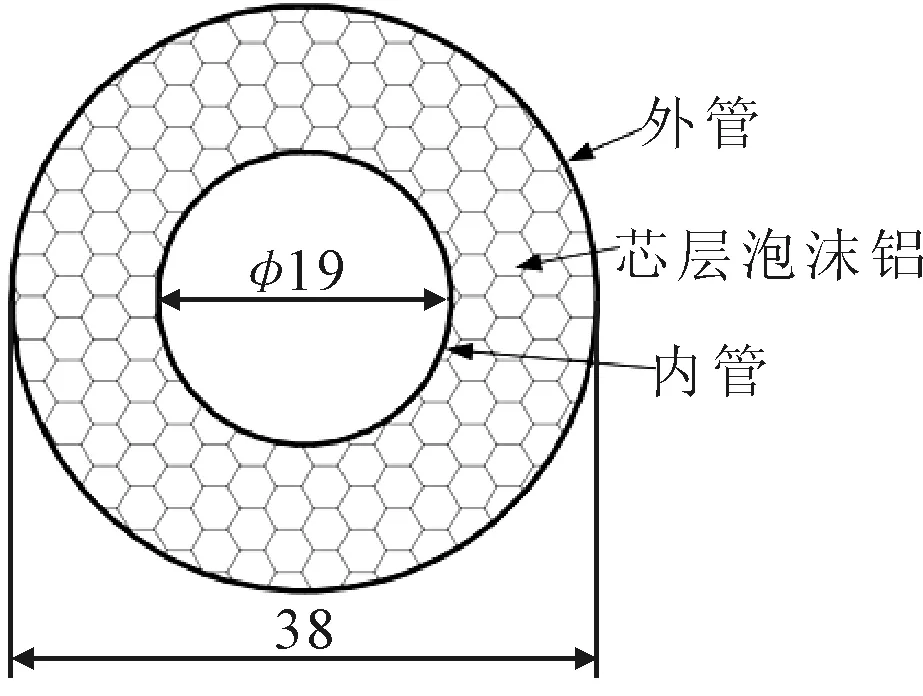
图2 横截面示意图
为了提高计算效率,又不失计算的准确性,对网格进行了局部加密.限制夹芯管两端所有位移和转动,冲头保持竖直方向的自由度,赋予其初始速度3.47 m/s.将冲头设置为离散刚性,赋予质量属性15.384 kg.为了进一步节省计算时间,冲头网格采用四边形为主的壳单元(R3D4).内外钢管采用四边形壳单元(S4R),芯层采用六面体单元(C3D8R).其有限元模型及边界条件见图3.
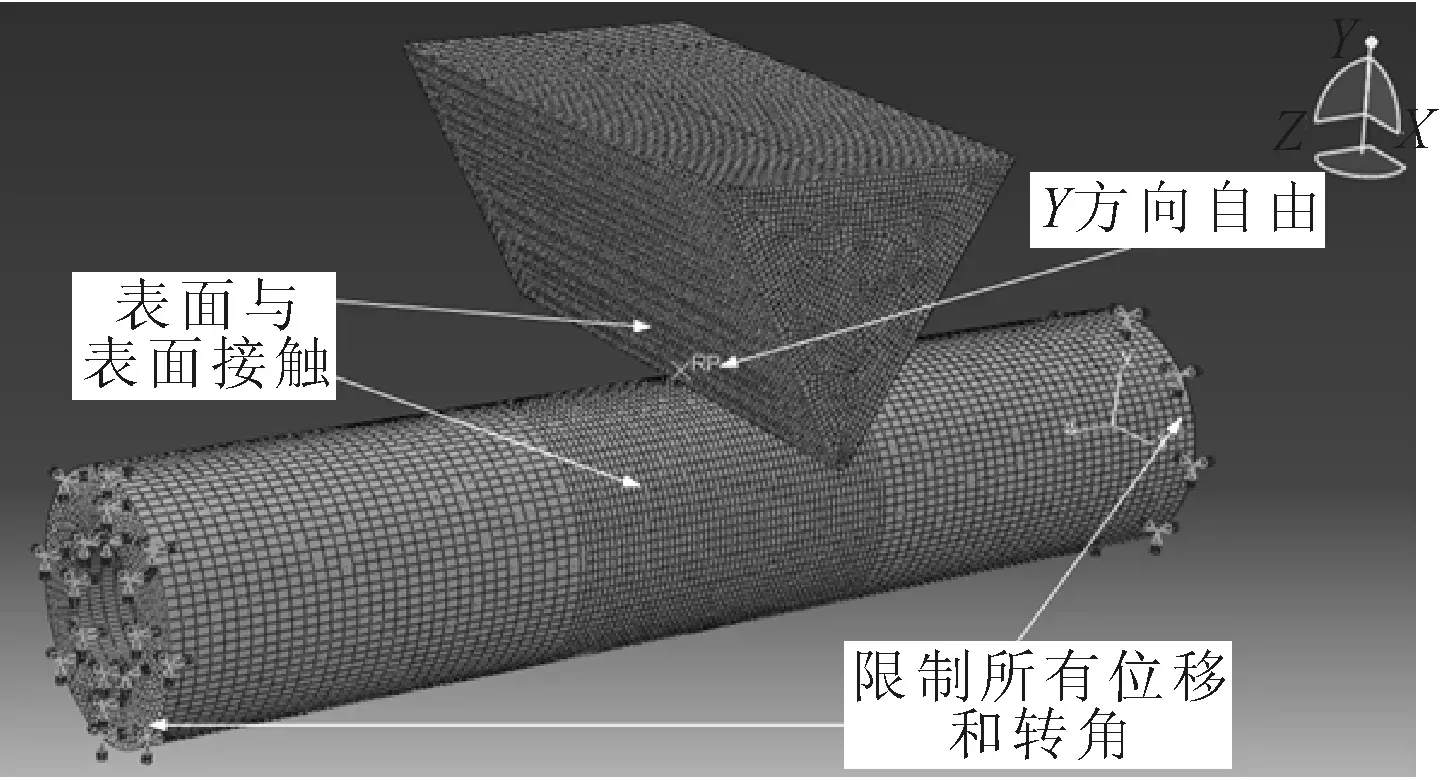
图3 有限元模型和边界条件
1.3 冲击过程分析
数值仿真方法可以对夹芯管横向冲击过程中的物理量进行监测,便于分析其动态响应过程.以下是对夹芯管冲击响应过程的分析.
图4为夹芯管受冲击的变形过程示意图,冲击时间长度设置为10 ms.由图4可知,t=0 ms时,冲头运动开始,冲头还未与夹芯管接触;t=3 ms时,冲头冲击夹芯管,夹芯管的变形持续增大,出现明显的局部凹陷;t=5 ms时,冲头的速度降为0,冲头的动能全部转化为夹芯管的弹性应变能和塑性应变能,夹芯管中点挠度达到最大值;t=10 ms,冲头反弹,已经与夹芯管分离,夹芯管的弹性应变能全部释放,转化为冲头的动能,冲头保持匀速远离夹芯管,夹芯管达到最终挠度.
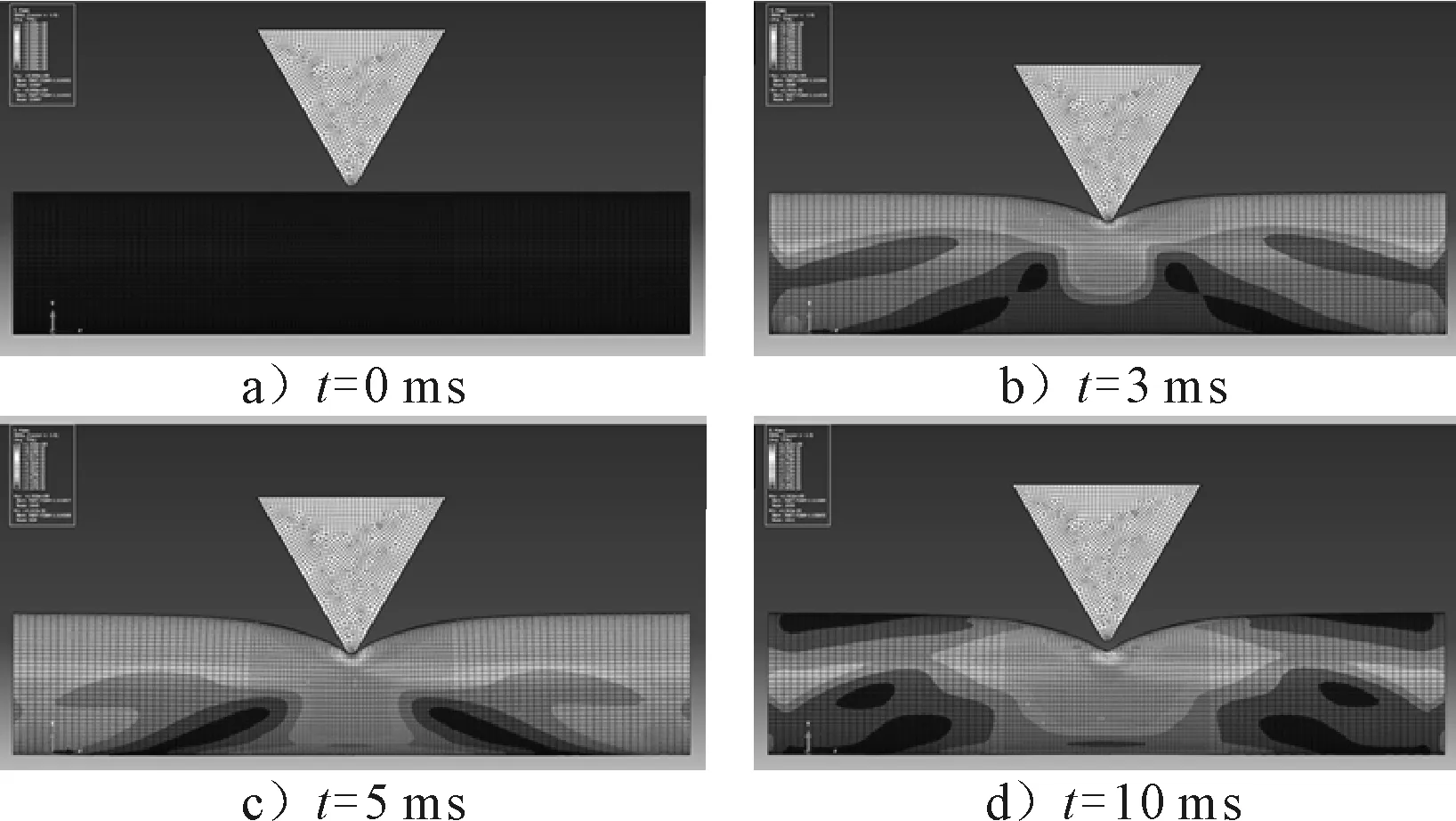
图4 夹芯管的变形过程
图5为夹芯管受横向冲击作用下的动态响应曲线.由图5a)可知,随着时间的增加,夹芯管各组成部分的变形逐渐增大,在达到最大值之后减小,冲头离开之后有轻微弹性振动,挠度趋于稳定.此外,外管中点处变形最大,其次是内管中点处变形.由图5b)可知,冲头以v0的速度与夹芯管接触后,冲头的速度不断减小,到0之后反向增大到vt,并匀速远离夹芯管.由图5c)可知,随着冲头与夹芯管接触,冲头的动能转化为夹芯管的变形能,在冲头速度降为0之后,夹芯管开始反弹,并将弹性应变能释放,转化为冲头的动能.此外,各部分吸收能量的大小关系为:外管>芯层>内管.
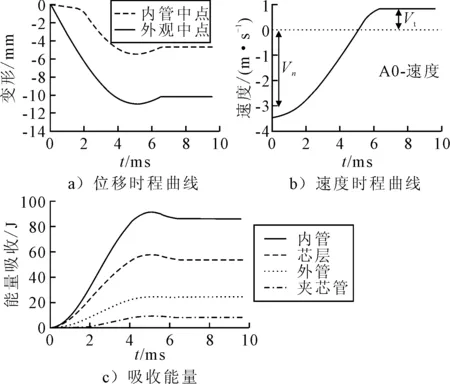
图5 动态响应曲线
2 数值仿真方法验证
利用INSTRON 9350冲击试验机进行了夹芯管的横向冲击实验,实验装置见图6.

图6 冲击试验机
泡沫金属夹芯管的总长度为350 mm,中间有效长度为180 mm.外管尺寸L×D×t为350 mm×38 mm×0.8 mm,内管尺寸L×D×t为350 mm×19 mm×0.6 mm,芯层厚度为8.5 mm.采用楔形冲头,楔形角为60°,底部倒角半径为1.5 mm,冲击总质量为15.384 kg.自行设计了四周固支夹具实现夹芯管的两端固支边界条件.
图7为冲击实验和数值仿真中获得的冲击力-时间曲线和冲击力-位移曲线的对比.由图7a)可知,对于力时程曲线而言,仿真中的冲击力变化趋势与实验基本吻合,仿真中的冲击力峰值偏大.另外,实验的冲击力曲线出现波动,这主要是在冲击过程中基座发生弹性振动造成的.由图7b)可知,在仿真与实验中获得的冲击力位移曲线变化趋势相似,位移值也基本相同.夹芯管的加卸载刚度十分接近,但是仿真中的加卸载刚度接近一条直线,这是因为数值方法中的是理想边界,不存在基座振动的影响.在卸载阶段,仿真中的冲击力-位移曲线存在明显的突变,而在实验中则是随着时间的增大而逐渐减小.这主要是因为夹具之间采用螺栓连接,螺栓的变形刚度与夹芯管的变形刚度不同,二者之间相互影响,因此存在卸载刚度渐变的情况.
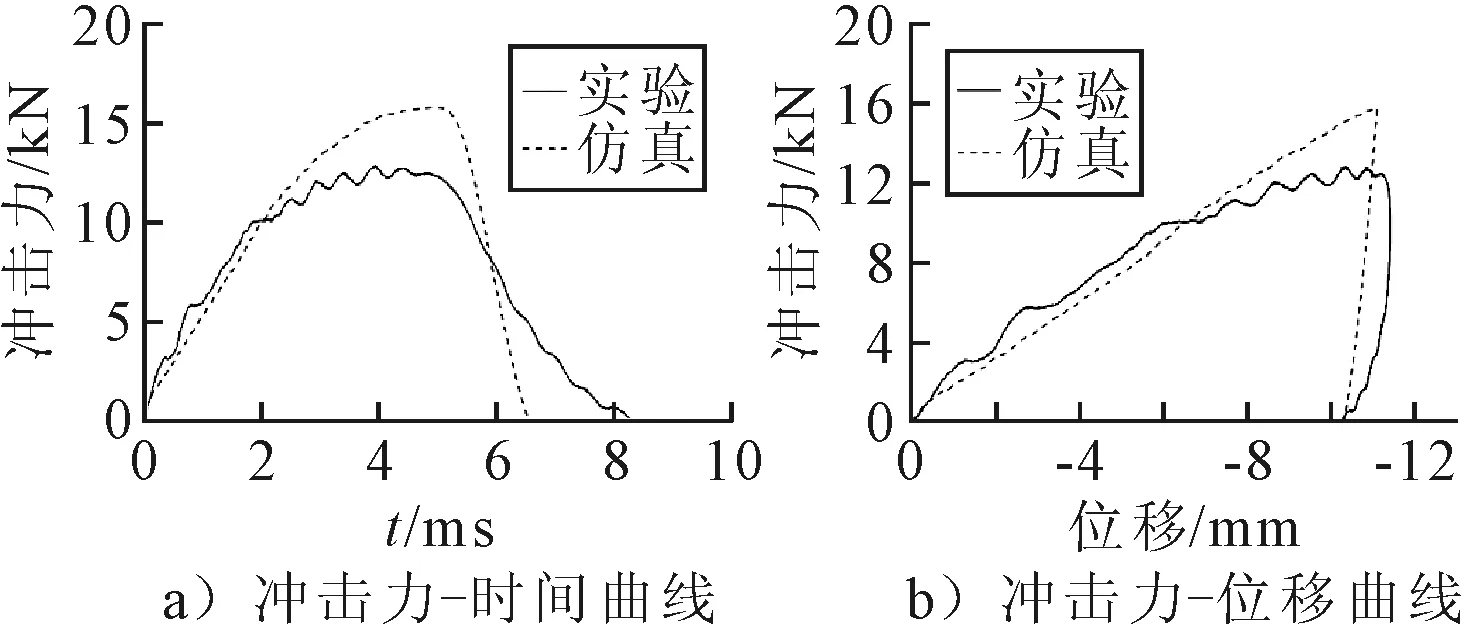
图7 实验和仿真结果对比
通过以上对比可知,仿真与实验结果基本吻合,最大挠度和最终挠度基本相同,而仿真的冲击力峰值偏大,其偏差为23.1%,其原因是实验中螺栓的影响,仿真中夹芯管的整体刚度大于实验,因此仿真获得冲击力峰值大于实验结果.从上述对比中可知,仿真与实验结果吻合较好.
3 影响参数分析
3.1 冲击能量的影响
夹芯管具有优良的能量吸收能力,不同的冲击能量下其冲击动态响应会有所不同,其变形模态和变形大小也有着较大的差异.通过改变冲头的速度来改变冲击能量.楔形冲头的质量为15.384 kg,冲击能量分为5组,从25~125 J,变化梯度为25 J.
图8为不同冲击能量下夹芯管的变形轮廓.由图8可知,夹芯管外管在不同冲击能量下的变形情况.
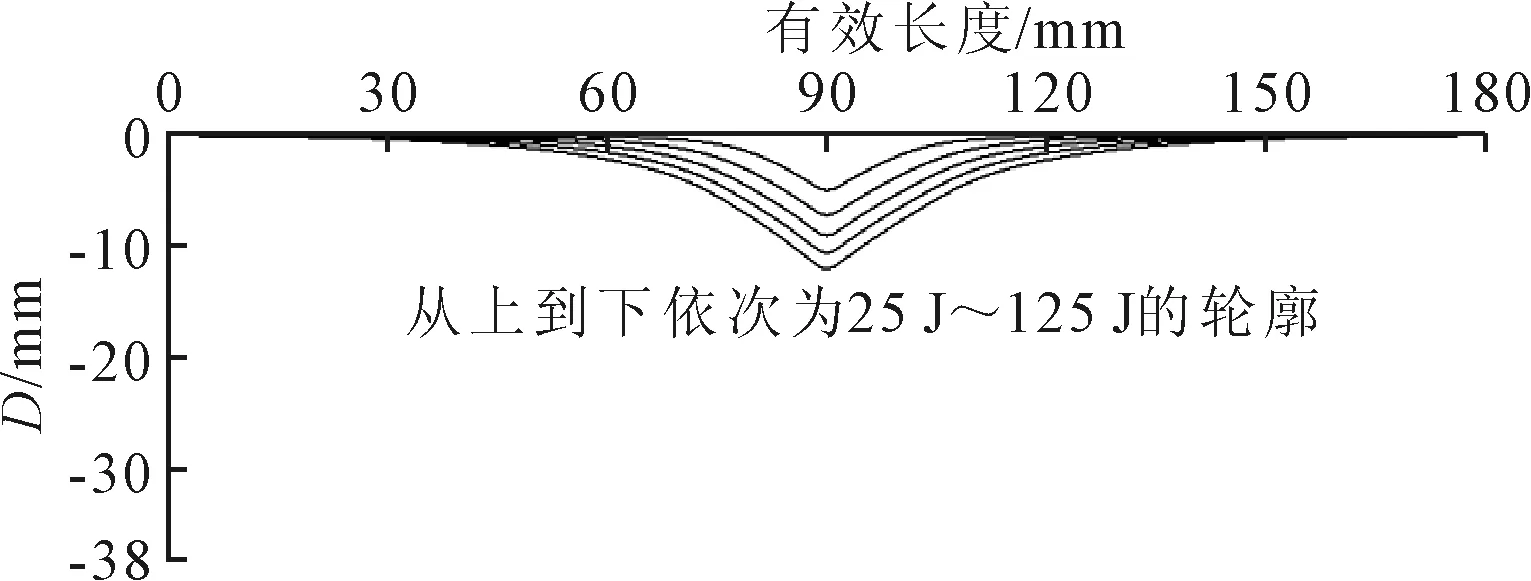
图8 不同冲击能量下的变形轮廓
图9为不同冲击能量下夹芯管的动态响应曲线.由图9a)~b)可知,随着冲击能量增大,冲击力增加和衰减的速率越快,冲击力峰值不断增加,但增加的幅度不断减小.进行数据拟合,冲击力峰值与冲击能量的关系可以得到式(1),符合乘幂增长规律;冲击持续时间基本保持不变.图9c)为夹芯管外管中点处的变形随着时间的变化曲线.由图9可知,夹芯管外管中点处变形先随着时间逐渐增大,在达到峰值之后,夹芯管开始释放弹性能,变形逐渐减小,直至冲头与夹芯管分离,挠度在很小的范围内上下振动.由图9d)可知,内管的变形先随着时间缓慢增长,在芯层基本被压实之后,与外管的变形规律相似.图9e)为内外管最终挠度随着冲击能量的变化规律.进行数据拟合,外管中点处最终挠度与冲击能量的关系符合式(2),满足乘幂增长规律;内管中点处最终挠度与冲击能量的关系符合式(3),满足线性增长规律.图9f)为夹芯管的冲击力随着冲头位移的变化曲线,其斜率表示加载和卸载过程中夹芯管的刚度.可以看出,随着冲击能量的增大,加载刚度相同,而卸载刚度有所增大.

图9 不同冲击能量下夹芯管的动态响应
从内外管中点处的最终挠度及其拟合曲线可以得知,当冲击能量低于某一个阈值时(EK=21.6 J),夹芯管外管产生变形,而内管无明显变形,这主要是因为芯层泡沫金属起到了缓冲作用,这也导致内外管挠度适合采用不同的拟合公式.
(1)
(2)
d=0.064 6EK-1.394
(3)
式中:EK为冲击能量;Fmax为冲击力峰值;D为外管中点处最终变形;d为内管中点处最终变形.
3.2 冲击位置的影响
为了研究泡沫金属夹芯管的动态响应与冲击位置的关系,以L/8为间距,进行了四种不同冲击位置下的数值仿真分析,冲击位置见图10.冲头质量为15.384 kg,冲击能量92.6 J.

图10 冲击位置示意图
图11为不同冲击位置下夹芯管的动态响应曲线.由图11a)可知,冲击位置靠近跨中时,不同冲击位置下冲击力的变化过程大致相同,但当冲击位置接近端部时(L/8),冲击力变化更剧烈.由图11b)可知,夹芯管外管和内管变形随着冲击位置的变化规律基本相同,但内管的变形随时间变化过程中具有芯层压实阶段的特征.冲击位置越接近端部,内外管的变形越小,当达到L/8时,变形已显著减小.由图11c)可知,冲击位置在离端部L/4~L/2范围时,内外管中点处的变形过程和最终位移基本相同.随着冲击位置靠近端部,最终位移逐渐减小.由图11d)可知,不同冲击位置下,夹芯管的冲击力-位移曲线变化趋势基本相同,冲击位置越靠近端部,夹芯管的加载刚度和卸载刚度越大.
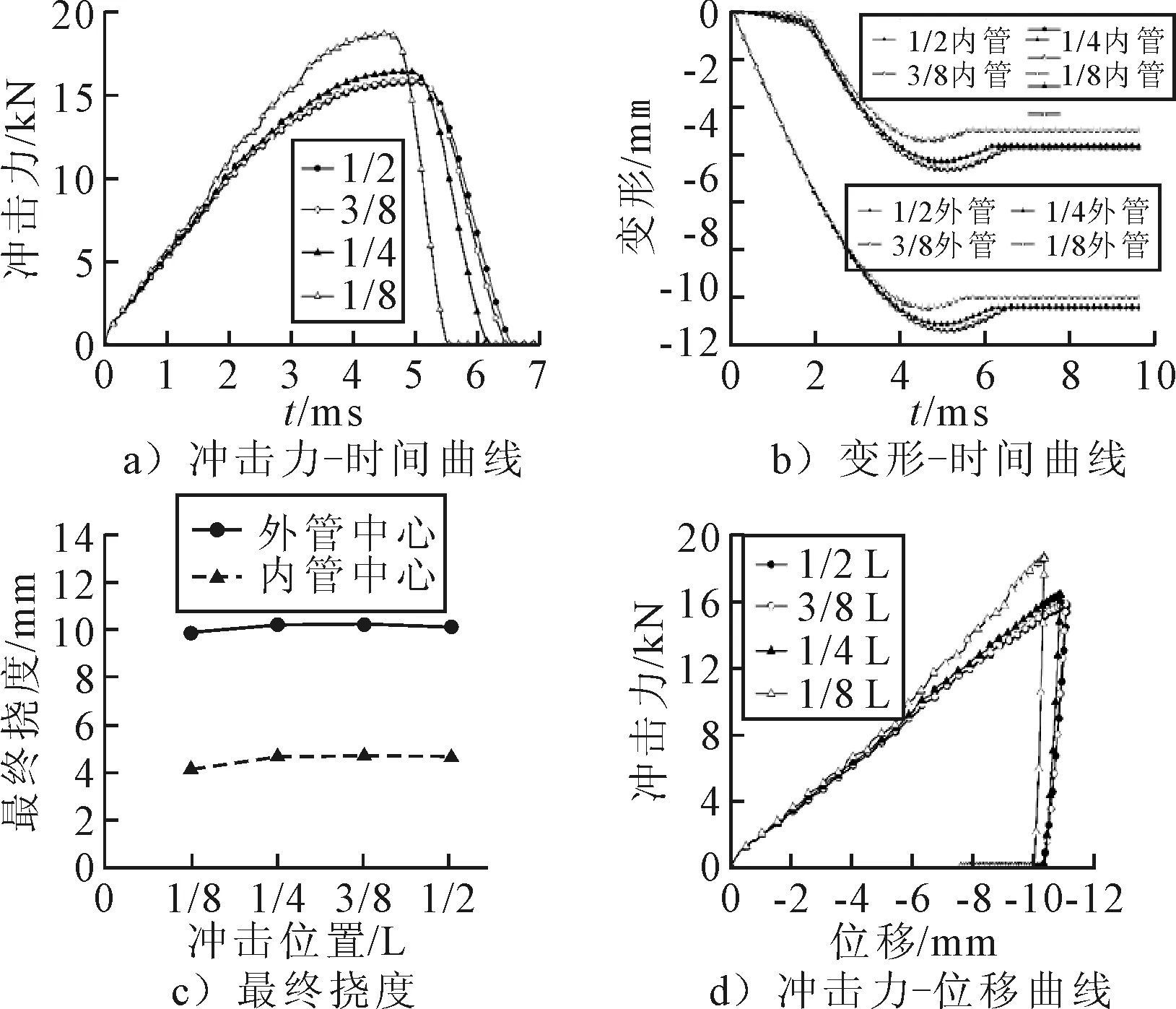
图11 不同冲击位置下夹芯管的动态响应
4 结 论
1) 泡沫金属夹芯管遭受横向冲击时,内外管以及芯层具有不同的变形模式.内、外管的冲击一侧出现明显的局部凹陷,而芯层出现局部压缩,夹层管的整体变形较小.在遭受外部冲击时,冲击能量大部分被外管和芯层吸收,内管吸收的能量较小,其产生的变形也相对较小,外管和芯层对内管起到了很好的防护作用.
2) 不同冲击能量下,加载刚度基本不变,而卸载刚度随着冲击能量的增加而增大.外管和内管的变形模态有所不同,外管中点处的挠度和冲击力峰值随着冲击能量的增加均呈现乘幂增长;内管中点处挠度呈现线性增长;冲击持续时间基本不变.
3) 冲击位置越靠近端部,加载和卸载刚度越大,外管和内管的变形模态相似.随着冲击位置靠近端部,冲击力峰值显著增加,夹芯管的最终挠度显著减小.

