V形柔性浮式防波堤消波特性研究*

冉小林 王 彬 段文杰 陈 凯 甘 进*

(武汉理工大学交通学院1) 武汉 430063) (武汉长江航道救助打捞局2) 武汉 430014)(武汉速安达建筑橡塑制品有限公司3) 武汉 430300)

0 引 言

浮式防波堤与其他传统防波堤相比，可适应水深较大、地基软弱、大潮差等水域，在港口海岸工程、海洋工程以及海水养殖等诸多领域具有广阔应用前景.其中柔性浮式防波堤由充水和充气囊体组成，其自身结构重量轻、储备运输空间小，并且展开撤收速度快，在临时浮式防波堤方面具有较好的应用价值.

现阶段对浮式防波堤的研究主要集中在防波堤的消波特性及防波堤新型结构上.Ataur等[1]利用水槽实验研究了不同锚缆系统、不同水深、不同波浪周期等条件下浮式防波堤的水动力性能.Abdullah等[2]通过遗传算法(GA)对双浮式防波堤水动力性能进行了优化结构设计.Nikpour等[3]采用二维波浪水槽试验对梯形浮式防波堤在深水规则波的衰减性能进行了综合试验研究.Christensen等[4]研究了带翼板和两侧附有的多孔材质对浮式防波堤反射和透射的影响.丁宁等[5]基于线性势流理论采用数值方法研究了V形浮式防波堤几何参数对其消波效果的影响.针对柔性浮式防波堤，现阶段的主要研究方法是通过模型试验的方法，何成圆等[6]针对一种由单囊体组合而成的柔性浮式防波堤，分析了此防波堤的消浪机理.杨浩[7]针对一种层铺式柔性浮式防波堤，通过物理模型的水池规则波试验，研究分析了此防波堤的相对宽度、波陡、上部浮板、波浪绕射等因素对防波堤的透射系数、反射系数、绕射特性以及防波堤的运动响应和锚链系泊力的影响.汪宏等[8]针对一种圆木阻尼式柔性浮式防波堤，通过二维水槽中的规则波物理模型试验，研究分析了该柔性浮式防波堤在有无浮板时的消浪性能.仇正中等[9]针对圆柱形柔性浮式防波堤的消浪特性，进行物理模型试验，研究分析其在规则波和不规则波作用下的消浪特性，通过大量水槽试验给出了圆柱形柔性浮式防波堤透射系数、反射系数、衰减系数与锚固方式、试验水深、相对宽度的变化关系.

文中采用模型试验和数值仿真相结合的方法对一种截面为圆形的V形柔性浮式防波堤的消波特性进行研究.在ANSYS-AQWA的线性三维辐射衍射模块[10-11]中建立了柔性浮式防波堤的数值计算模型，在频域内研究了防波堤的消浪性能，讨论并分析了此数值方法的计算结果与试验结果之间的关系，提出采用此数值计算方法来评估柔性浮式防波堤消浪性能的可行性.

1 分析模型及分析方法

1.1 分析模型

实验模型见图1，消波装置主要由下部主水囊和上部为水囊提供浮力的两个气囊组成，单个浮体总长4 m，下部水囊直径 0.4 m，上部气囊直径为0.1 m.试验中采用了两种布置方式：①V形布置，即两水囊一端相连，形成V形结构，V形首部正对着波浪入射方向，V形的夹角分别为30°，45°和60°;②单水囊迎浪横向布置.

数值计算模型采用前期开展的实验模型.由于试验过程中水池宽度为10.8 m，防波堤在水池宽度方向上的最大尺寸为4 m，相较于水池宽度，模型尺寸较小，且水池壁面上安装了消浪装置，以此避免波浪传递到水池壁面后反射波对试验模型的影响，因此在数值模拟过程中，忽略水池壁面对防波堤计算模型的影响，数值计算模型见图2.

图1 试验模型

图2 数值计算模型

考虑锚泊系统对防波堤消波效果的影响，根据实验中锚泊缆绳的布置方式，数值计算模型缆绳布置情况见图3.试验过程中水池水深为2 m，因此数值模型计算水深设为2 m，迎浪方向为X轴正向.由于防波堤下部主囊体为水囊，实际消波过程中，下部水囊完全浸没于水中，依靠上部提供浮力的气囊保证消波装置的正常漂浮，因此试验和数值计算中结构的吃水为0.4 m，同时，实际消波过程中上部的气囊也参与了消波，图4为柔性浮式防波堤截面示意图.

图3 防波堤锚泊缆绳布置情况

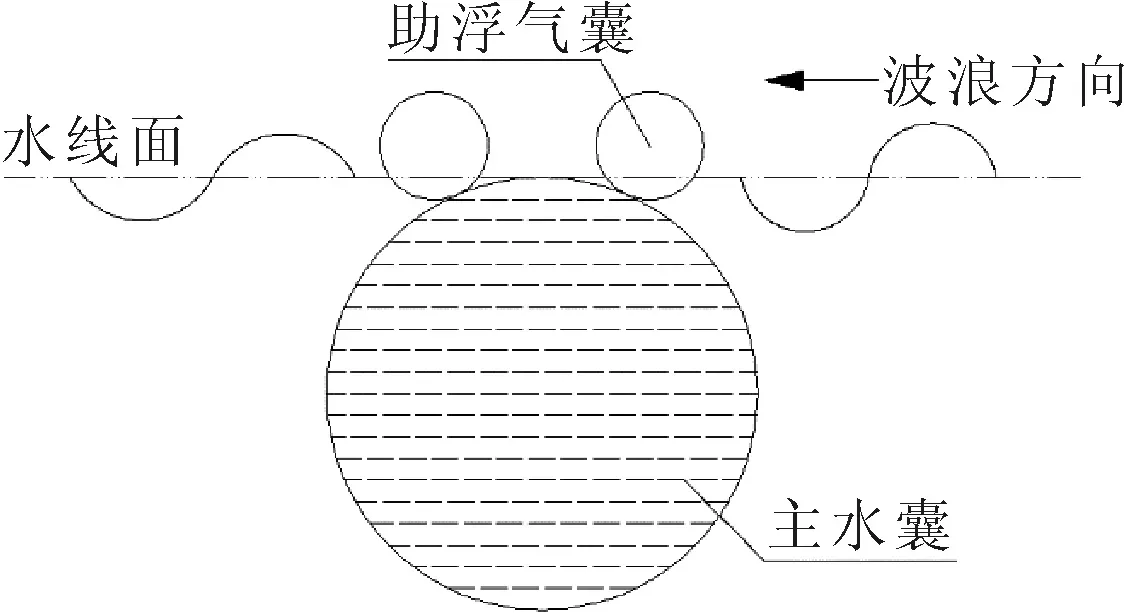
图4 柔性浮式防波堤截面示意图

1.2 数值分析方法

ANSYS WORKBENCH AQWA将AQWA的各个主要模块集成在Hydrodynamic Diffraction和Hydrodynamic Response模块中，功能完备，界面非常友好，易于操作.其Hydrodynamic Diffraction模块主要进行浮体的辐射衍射分析，可计算得到浮体的相关水动力系数、浮体的静态和动态响应问题，以及波浪传递给浮体的表面压力等.Hydrodynamic Response模块可以进行浮体的平衡分析，在辐射衍射分析基础上给浮体结构添加锚泊系统，可计算得到锚泊状态下浮体的静水平衡位置、锚泊缆绳的张力，以及进行浮体的静稳性分析.

由于在Hydrodynamic Diffraction中系泊缆绳无法参与计算，如需考虑锚泊系统对防波堤消波效果的影响，可以在辐射衍射分析模块的Connection菜单中添加连接刚度考虑系泊系统的影响.本文柔性浮式防波堤首先在Hydrodynamic Diffraction模块进行辐射衍射分析，然后在Hydrodynamic Response模块进行平衡分析并且提取锚泊刚度后添加到Hydrodynamic Diffraction模块再进行辐射衍射分析，最后采用AQWAGS进行后处理，输出沿波浪入射方向波浪幅值的变化曲线，通过提取波前和波后的波浪幅值，就可得到防波堤的消波效率.

AQWA进行辐射衍射分析是纯线性分析，计算的是规则波浪下的自由液面高度，最终输出的结果是波幅值随入射波方向的位置关系曲线.由公式H=Asin 2πft可知波面只是某一相位的函数，而波高幅值A是稳定不变的，输出的幅值可代表此坐标位置的波高值.由波浪幅值随入射波方向的位置关系曲线可得到堤前入射波高Hi和堤后平稳的波浪幅值Ht，进行相比得到波浪的透射系数Kt=Ht/Hi,继而得到了防波堤的消波效率η=(1-Kt)×100%，即可表示柔性浮式防波堤的消波效果.

2 结果分析

试验中，通过在防波堤堤前和堤后布置的多个浪高仪，可测量出试验过程中防波堤堤前入射波高Hi和堤后平稳的波浪幅值Ht，通过计算便可得到防波堤的消波效率，图5为试验过程中进行堤前和堤后波高幅值的测量.

图5 试验中波高幅值的测量

利用AQWA分别建立夹角为30°，45°，60°的V形布置方式和单一囊体迎浪横向布置的计算模型，将数值计算结果与试验结果相比较，验证此仿真方法的可行性和准确性.在计算消波效率时，使用AQWAGS打开模型的辐射衍射分析计算结果，得到波高幅值云图，见图6.提取波浪幅值沿波浪方向(即X轴负向)的变化曲线，可得到堤后的波高幅值，便可计算得到防波堤的消波效率，见图7.由图7可知，60°夹角布置方式下V形柔性浮式防波堤在波高0.075 m和波浪周期1.342 s的规则波作用下，波幅随X轴的位置变化曲线，曲线的横坐标为沿波浪入射方向X轴的各点坐标值，纵坐标为各点对应的波幅值，为入射波、衍射和辐射波的总和.图7中的波高幅值变化曲线是有波动的曲线，是因为在仿真分析中由于入射和反射等不同波的叠加导致每个位置的波幅都有轻微的变化，导致曲线有些波动，以至于堤前的曲线类似于正弦的曲线，但是能明显的观察到堤后的波幅值要明显的小于堤前的波幅值，并随X轴坐标值的减小趋于稳定.根据结果显示，堤前的大多位置的波幅值都大于实际计算设置的入射波的波幅值0.075 m，这是由于入射波与堤前反射波叠加导致的.

图6 波高幅值云图

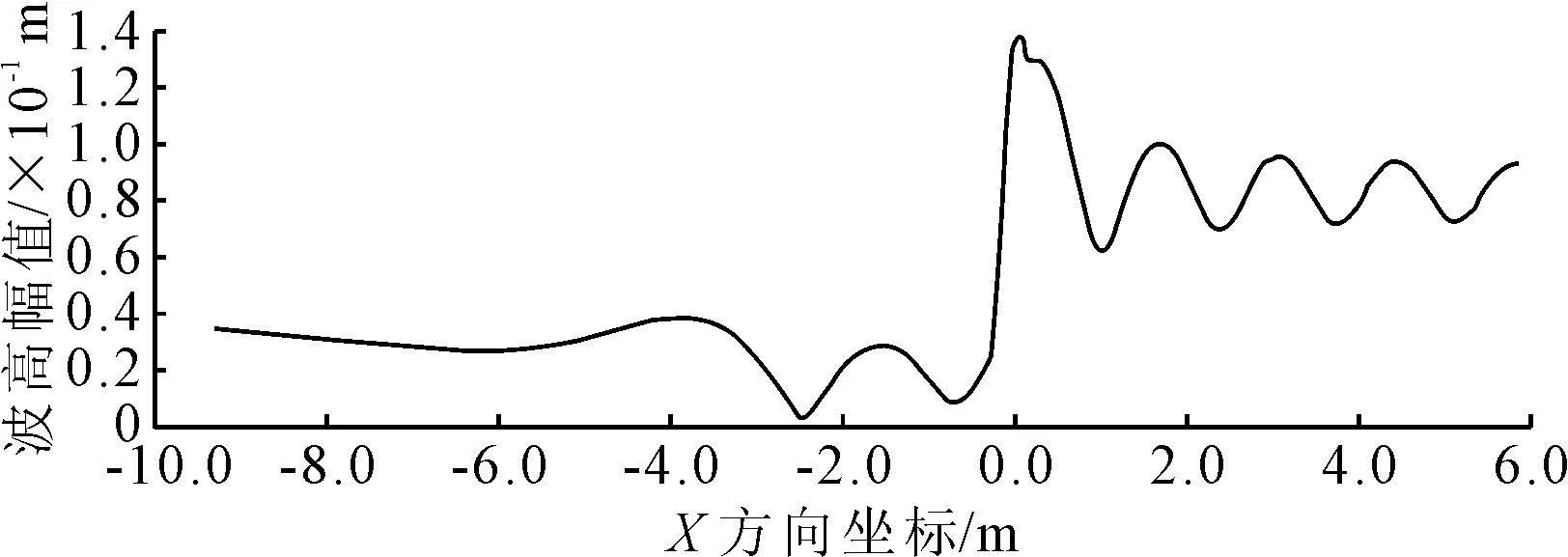
图7 波浪幅值沿波浪方向变化曲线

为了研究柔性浮式防波堤的消波机理以及为柔性浮式防波堤设计提供技术参考，将主要探究不同波浪周期对柔性浮式防波堤消波效果的影响，不同波高对柔性浮式防波堤消波效果的影响，以及不同布置方式对柔性浮式防波堤消波效果的影响.同时，将数值计算结果与试验结果进行对比分析，验证此数值仿真方法的可行性和准确性.

2.1 波浪周期对防波堤消波效果的影响

试验和数值分别计算了波高0.075 m、波浪周期T=1.118，1.342，1.565，1.789 s下柔性浮式防波堤的消波效率，见图8.

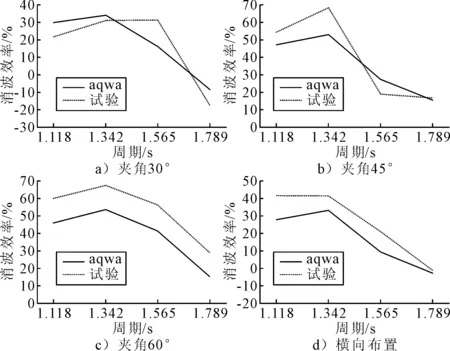
图8 波浪周期对消波效率的影响

数值和试验结果表明，不同布置方式下防波堤消波效率都随波浪周期的增加呈现先增加后减小的趋势，在周期T=1.342 s时的消波效果最好.从整体数值计算结果上看，数值模拟计算得出的消波效率较物理试验结果普遍偏小，其误差值在6%～15%，这是由于物理试验存在能量损耗，包括自然消耗和试验水池等试验设施对波浪能的消耗，然而在数值仿真中只有防波堤能吸收波浪能量，外界不吸收波能，以及试验中波浪产生的摩擦破碎所消耗的部分能量在数值仿真中无法考虑.再加上试验中防波堤采用的是充压水囊，是柔性结构，波浪作用于防波堤时会导致囊体有明显的变形，会吸收掉部分的波浪能，而在AQWA数值计算分析中，计算模型是以刚体结构考虑的，波浪作用于防波堤时，结构不会产生变形而消耗掉部分波浪能，以至于数值计算得到的消波效率较试验结果普遍较小.

2.2 波高对防波堤消波效果的影响

通过计算波浪周期T=1.342 s不同布置方式下，不同波高对柔性浮式防波堤消波效果的影响曲线，发现随着波高的增大，四种布置方式下防波堤的消波效率都有相对的减小，但差别不大，见图9.在数值分析中，这主要因为AQWA的辐射衍射分析中求的解是单位波高的解，而后处理中是根据设置的不同波高值来乘以相应的系数.试验中，由于测量和试验中不可控制的外界因数，导致试验结果个别点有些差异，但整体上变化趋势与数值结果相同，随着波高的增加，消波效率只是有相对的减小，但数值上相差不大.将数值计算结果与试验结果比较分析发现，整体上数值结果与试验结果具有较好的相关性，不同波高下数值计算得到的消波效率较试验结果偏小，其误差值在6%～15%.

图9 波高对消波效率的影响

2.3 布置方式对防波堤消波效果的影响

图10～11分别为不同布置方式下波浪周期和波高对防波堤消波效果的影响曲线，从整体上看，在同等波浪工况下，V形布置防波堤的消波效果优于迎浪横向布置防波堤的消波效果.V形布置防波堤在同波浪工况下，夹角为45°和60°的V形防波堤的消波效果优于夹角为30°的防波堤，夹角为60°的防波堤消波效果最好.V形布置的防波堤，在一定程度上对波浪起到了分离的作用，从而改变了波浪的传播方向，实现对防波堤遮蔽区域的保护作用，以至于V形布置防波堤的消波效果比迎浪横向布置较好.但同时由于夹角相对较小时，防波堤对波浪的分离较差，且波浪在防波堤端部引起的回流、湍流和紊流对遮蔽区域影响较大，导致小夹角防波堤的遮蔽区域以及堤后的消波效果相对较差.

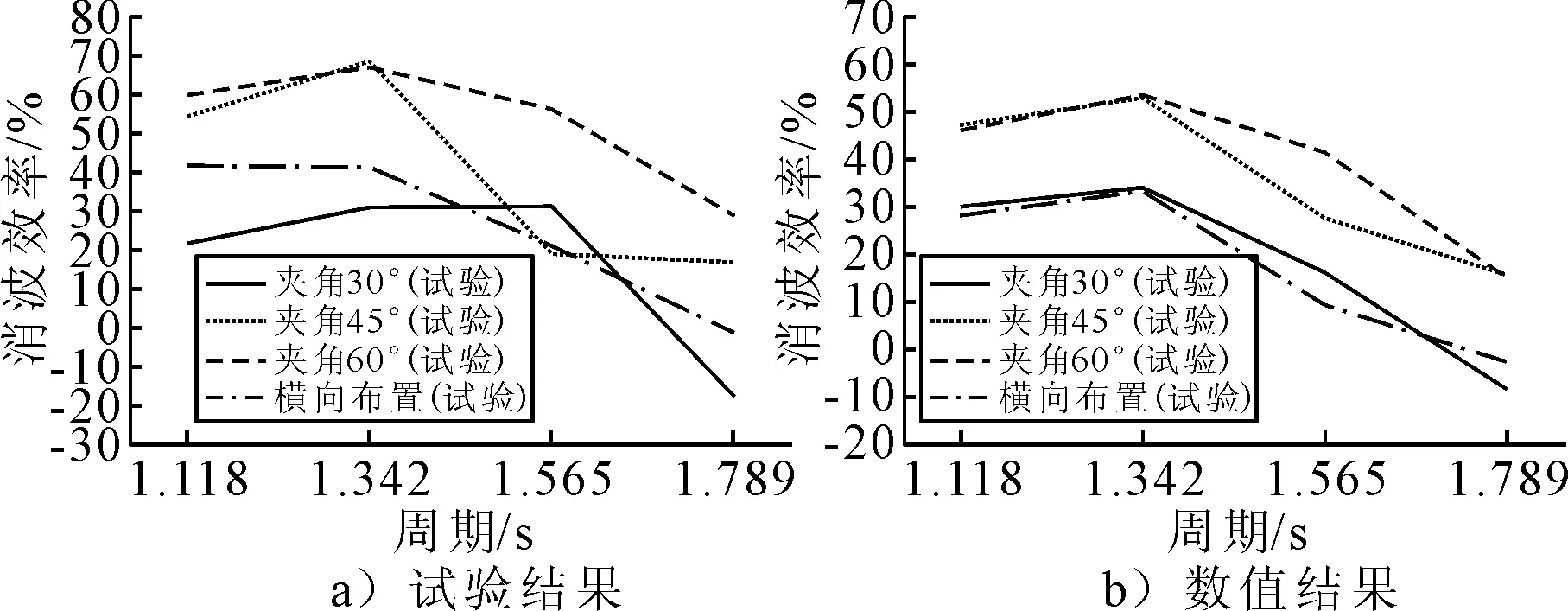
图10 不同布置方式下周期对消波效率的影响

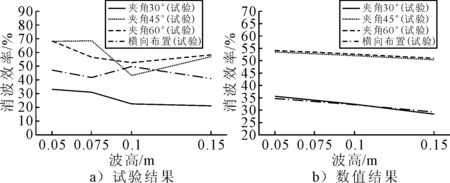
图11 不同布置方式下波高对消波效率的影响

3 实际模型计算分析

3.1 计算模型及计算工况

前面的试验和数值仿真模型尺寸是根据实际结构按一缩尺比缩小得到的，针对工程实际应用的柔性浮式防波堤结构尺寸，建立其AQWA数值计算模型，计算分析实际结构尺寸及工况下柔性浮式防波堤的消波特性.根据国际通常的海洋工程试验缩尺比60～80的原则，同时又为发挥拖曳水池的优势、减小尺度效应以及方便实验的实施，前面开展的实验缩尺比λ设定的为20，进而根据缩尺比来确定的实验模型尺寸，即：

式中：L，B，d，H，T分别为防波堤的长、宽、吃水以及波高和周期等波浪参数.

实际模型单个浮体总长80 m，下部水囊直径8 m，上部气囊直径为2 m，结构吃水8 m，计算水深也按缩尺比λ进行缩放，实际模型计算水深为40 m，计算模型和锚泊缆绳布置情况见图12.同时也分别计算了两种布置方式，一种为V 形布置， V形的夹角分别为30°，45°和60°，另一种为单囊体迎浪横向布置.

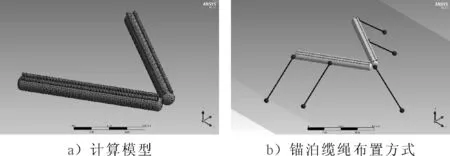
图12 实体计算模型及锚泊缆绳布置情况

实体模型计算工况根据缩尺比换算得到，计算工况见表1.

表1 实体模型计算工况

3.2 计算结果及分析

进行实体模型的辐射衍射分析，通过AQWAGS得到实体模型的计算结果，图13～14分别为45°夹角布置方式下V形柔性浮式防波堤在波高1.5 m和波浪周期6 s的规则波作用下，实体模型波高幅值云图以及波幅随入射波方向X轴的位置关系曲线.从计算结果可以看出，堤后的波幅值要明显的小于堤前的波幅值，防波堤具有较好的消波效果，通过防波堤对波浪进行衰减后，堤后的波浪幅值逐渐趋于稳定，并且在其遮蔽区域消波效果较好.

图13 实体模型波高幅值云图

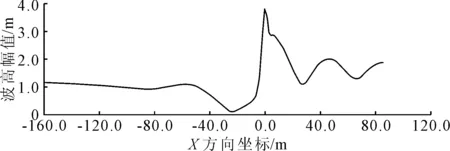
图14 实体模型波浪方向波高幅值变化曲线

实体模型分别计算了波高1.5 m波浪周期T=5，6，7，8 s的不同布置方式下防波堤的消波效果，见图15a)，与试验模型数值计算结果相比，见图15b)，从计算结果整体上看，实体模型数值计算结果与前面的试验模型数值计算结果具有较好的相关性以及吻合性，除了横向布置下的消波效果随波浪周期的增加呈递减趋势，其它布置方式下消波效果随波浪周期的增加呈现先增加后减小的趋势，在周期T=6 s时的消波效果最好，而后减小.在夹角为30°和60°的布置方式下，实体模型计算结果与试验模型数值结果吻合较好，可视为等效，其夹角45°和横向布置方式的结果值虽然与试验模型计算结果有一定的差异，但变化趋势及规律总体相同.由于实体模型与试验模型间的相关尺寸及载荷等参数是通过缩尺比换算得到的，其计算模型结构之间必然存在尺度效应，再加上计算工况以及锚链等参数间的换算等因数都对计算结果产生一定的影响.

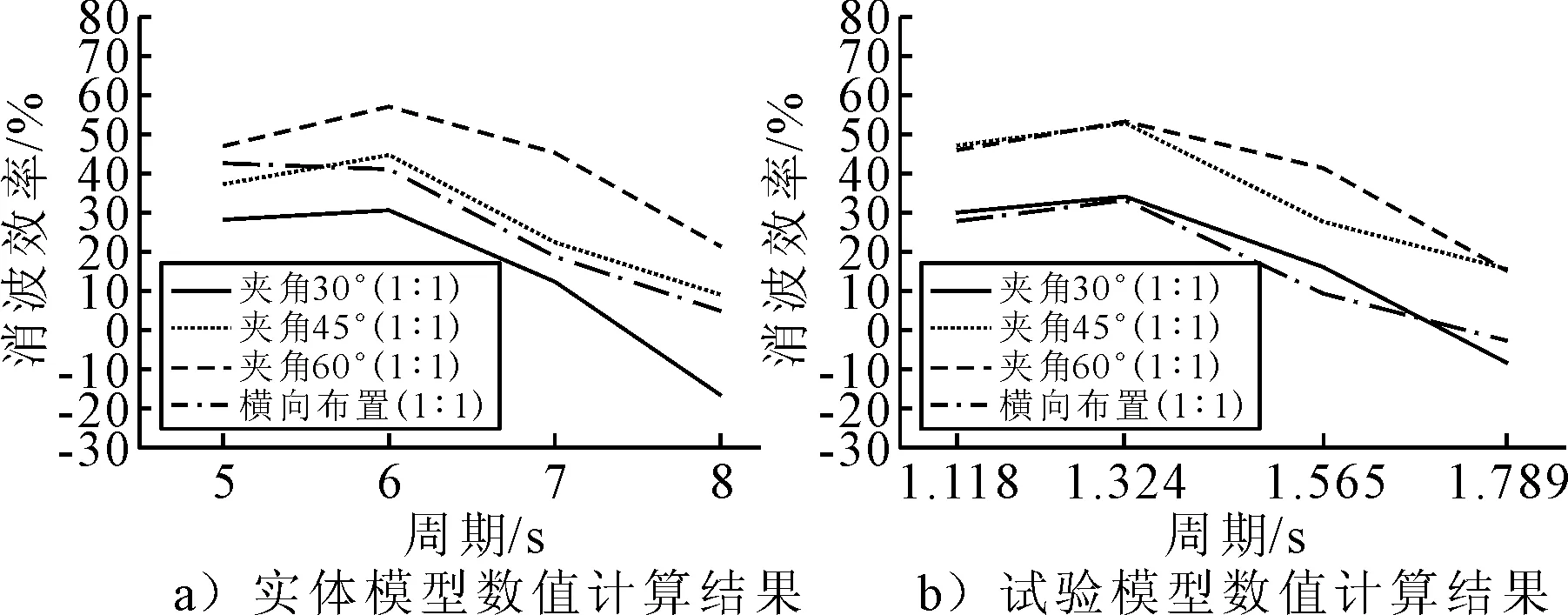
图15 不同布置波浪周期对消波效率的影响

同样在实体模型中，计算了波浪周期为6 s，不同布置方式下不同波高对防波堤消波效果的影响曲线，见图16a)，发现随着波高的增大，四种布置方式下防波堤的消波效率都有相对的减小，但差值别不大，与试验模型数值计算结果相似.同样是因为AQWA的辐射衍射分析中求的解是单位波高的解，而后处理中是根据设置的不同波高值乘以相应的系数.

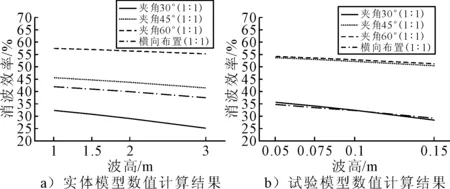
图16 不同布置波高对消波效率的影响

通过图15a)和图16a)的实体模型在不同布置方式下消波效率随波浪周期和波高的变化曲线可以看出，夹角为60°的V形柔性浮式防波堤的消波效果优于其它布置方式，在工程实际过程中，其为首先结构形式，并随着夹角的减小，V形柔性浮式防波堤的消波效果也相应的降低.

4 结 论

1) 不同布置方式下柔性浮式防波堤的消波效率随波浪周期的增加呈现先增加后减小的趋势，防波堤对短周期波消波效果较好，在周期T=1.342 s时的消波效果最好.

2) 由于AQWA的辐射衍射分析中求的解是单位波高的解，而后处理中是根据设置的不同波高值乘以相应的系数，以至数值分析中波高对防波堤消波效果的影响较小，随着波高的增大，其值只是相对的减小，但差值不大.

3) 数值模拟计算得到的消波效率较物理试验结果普遍偏小，其误差值在6%～15%.

4) 夹角为45°和60°的V形柔性浮式防波堤的消波效果优于夹角为30°和单一囊体迎浪横向布置的柔性浮式防波堤，夹角为60°的防波堤消波效果最好.

5) 夹角为60°的V形柔性浮式防波堤的消波效果优于其他布置方式，在工程实际过程中，其为首先结构形式，并随着夹角的减小，V形柔性浮式防波堤的消波效果有相应的降低.