船舶主机安装高度偏差对轴系装调的影响分析
邓义斌 杨小钢 黄燕玲 朱汉华 范世东
(武汉理工大学能源与动力工程学院1) 武汉 430063) (武汉市船舶检验所2) 武汉 430030)
0 引 言
船舶推进装置安装是船舶建造过程的重要环节,其安装质量直接影响船舶的推进性能,为此造船企业形成较为完整的安装工艺流程和质量控制措施,各船级社都制定较为严格的安装检验规范[1-3].但受限于船舶建造的精度,主机实际安装高度与设计高度会产生偏差[4-6].该偏差将影响轴系校中质量[7-8],同时在一定程度上压缩中间轴承调整的试错空间,增大轴系的装调难度,导致轴系安装工期长、装调效率低,文献[9]报道某轮中间轴承调整用时长达35 d的情况.因此,分析主机安装高度偏差对轴系装调的影响,对于制定合理的装调决策、提高船舶推进装置的安装质量和效率具有重要意义.
1 主机安装高度偏差原因
以国内造船厂应用较为广泛的艉艏安装工艺为例来说明船舶推进装置安装过程,船舶下水前,先在船台确定轴系理论中心线,确定轴系理论中心线通常采用以艏、艉两基准点作为依据的拉线法或光学法;然后按已确定的理论中心线在船体上镗孔以便轴系进入船体,再安装艉轴管、艉轴、艉轴承等装置;船舶下水后,以艉轴端为基准,按规定的偏移值和曲折值由艉至艏逐个轴段进行联接,找准主机及吊装,开展轴系校中,如果校中检验不合格,则需要根据检验结果来制定调整方案.通过调整中间轴承高度或甚至调整主机高度重新找准主机,直至校中检验合格,然后固定主机,其主要流程见图1.

图1 船舶轴系艉艏安装工艺流程图
基于该工艺流程主机安装高度偏差产生的原因为:①轴系理论中心线是在船台上确定的,但船舶下水后船体支撑状态发生变化,导致船体发生变形,按变形前确定的位置安装主机则会产生偏差;②主机吊装后由于重量增加使安装主机分段的船体局部发生变形,同理该变形也产生偏差;③由于加工及安装精度不易控制,难以避免存在偏差.
2 主机高度偏差影响
2.1 轴系受力
设轴段端面的应力-应变状态可由轴系垂向位移z、截面转角θ、弯矩M和剪力T表示.轴段仅受重力影响、受集中载荷单元与支承单元的传递矩阵分别如式(1)~式(3)所示[10-12].
(2)
(3)
式中:li为第i轴段单元的长度;qi为第i轴段单元的均布载荷;EIi为第i轴段单元的抗弯刚度;P为集中载荷;ke为支承的等效刚度;δ为某轴承安装前向下的移动量.结合连续条件(4),便可求出任意单元端面的状态参量与初始量的关系(5).
(4)
(5)
式中:ti为第i单元的传递矩阵.
对于主机端支承,使得其变位z0=1,其他参量取0,列出轴承跨距累积矩阵,可得式(6).
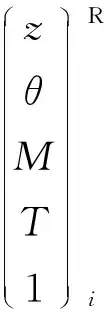
(6)
综合式(1)~式(6),可得主机高度偏差大小对各轴承受力的影响:①当轴系材料仅发生弹性形变时,主机高度变化与各轴承受力变化为线性关系;②各支承等效刚度大小相近时,主机高度偏差对各轴承受力的影响从艏向艉传递随距离增大逐渐变小,并且相邻轴承的影响因子不同号.
2.2 变位调整
1) 中间轴承变位试错空间 根据船级社相关规范,轴承受力应处于轴系校中计算书设计值允许的偏差范围内.仅考虑单个轴承自身的受力与变位条件下,当主机及各轴承均位于设计高度时各轴承变位试错空间是以设计轴承高度为基准点,由轴承受力允许偏差确定的轴承变位上下限;而当主机安装高度存在偏差各轴承仍位于设计高度时,根据2.1分析,该偏差将使轴承受力偏离设计值,导致试错空间发生平移,此时如果仍按原来的试错空间去调整轴承变位,则会出现小部分空间不能满足轴承受力的规范,此时试错空间应缩小为平移前后的交集,见图2.
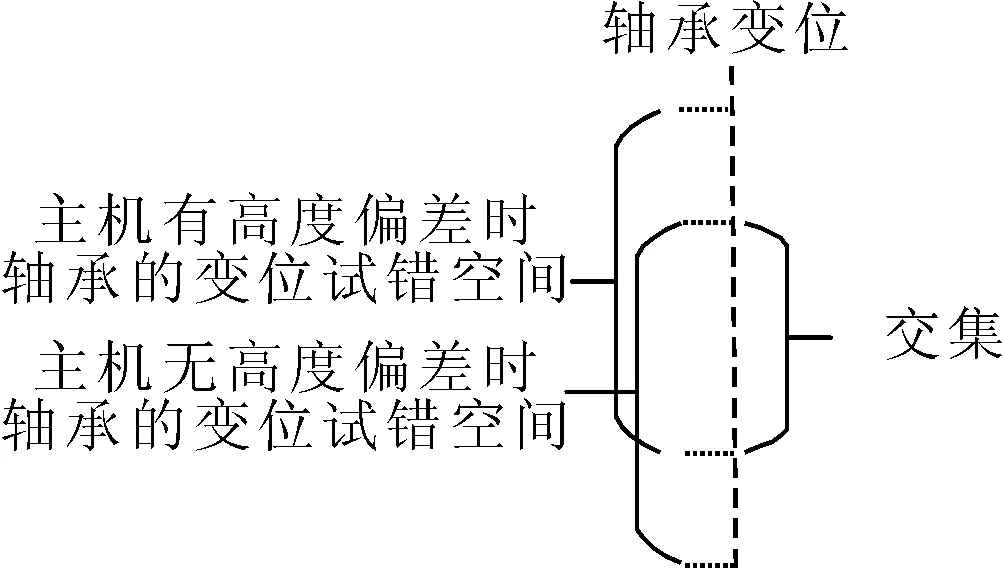
图2 轴承变位试错空间变化示意图
2) 主机变位决策 主机高度偏差在压缩中间轴承试错空间的同时,也会影响艉轴承受力,当偏差过大时,将导致艉轴承受力超出规范允许的范围,而艉轴端作为基准一般不作调整,使轴系安装基准点的艉轴承受力超出规范的主机高度偏差称为临界高度偏差,当主机安装高度偏差超出临界偏差时需要先调整主机高度以降低轴系校中难度.
3 实例计算
3.1 各轴承受力影响计算
以一艘汽车滚装船推进轴系为实例进行计算.该轮轴系布置见图3,全长54.3 m,设有三个中间轴承和三个艉轴承,轴系的力学参数见表1.

图3 推进轴系结构简图
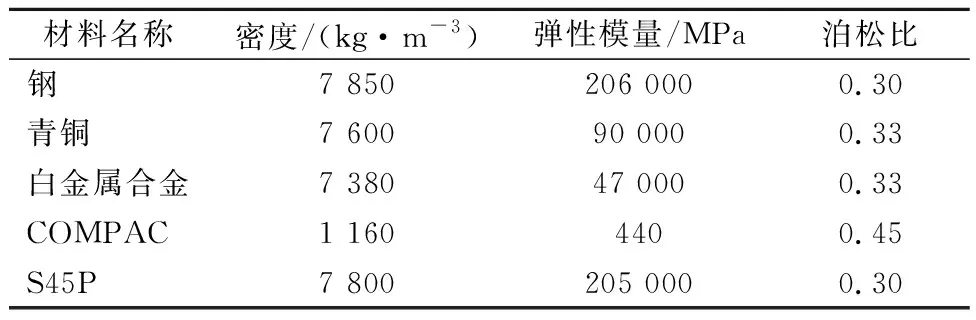
表1 各材料力学性能参数
按轴系的设计参数,设定艉轴承与中间轴承高度均为0 mm,主机及曲轴高度设为轴系计算书的给定数值,用传递矩阵法计算得到主机高度偏移+0.1 mm时各轴承受力变化值见表2各轴承受力的影响规律与理论分析结果完全一致,1#和2#艉轴承与主机距离较远,主机安装高度偏差对其受力的影响可忽略不计.

表2 各轴承受主机高度偏差的受力影响因子 单位:kN
3.2 各中间轴承调整试错空间影响计算
根据2.2的分析条件,分别计算主机安装高度无偏差与偏差+0.1 mm时轴承变位试错空间变化见表3.
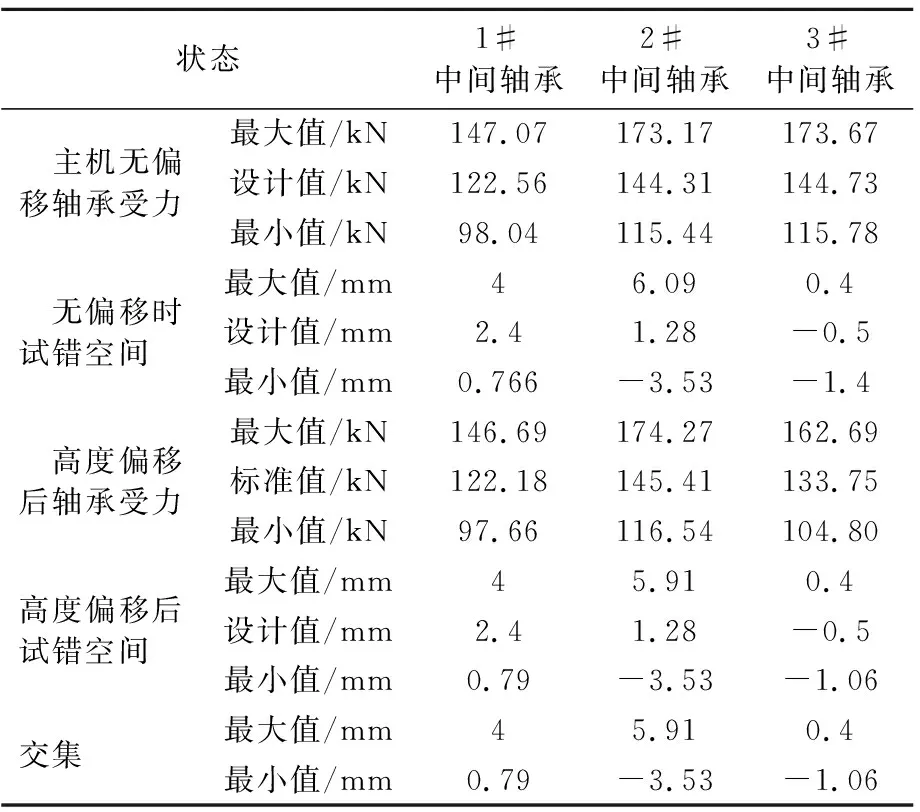
表3 中间轴承试错空间变化
主机高度无偏移时,各中间轴承受力允许范围为设计值的±20%.主机高度偏差+0.1 mm时,中间轴承受力将偏离设计值,称其为标准值,将标准值加上设计值的±20%,可求得按原变位调整轴承受力的最大值与最小值.通过各中间轴承自身受力变化影响因子及允许受力范围,可求得各中间轴承在设计值时上下调整的空间.取主机高度正常与偏移+0.1 mm时的试错空间交集,可得到主机高度变化+0.1 mm时,1#、2#和3#中间轴承试错空间分别减小0.026,0.18,0.34 mm,试错空间分别压缩了0.8%,0.19%,18.9%.
3.3 主机高度临界偏差计算
按2.2的分析,假设所有艉轴承高度均为0 mm,各中间轴承支撑点连线为直线,3#艉轴承受力超出规范允许的范围时达到临界状态.若主机安装高度无偏差,则轴系安装状态为如图4所示的水平直线;主机安装高度有偏差时,轴系安装状态为如图4所示的斜线.

图4 轴系轴线状态变化
由主机高度偏差引起的各中间轴承高度的变化可以利用相似三角形计算得到,并由此计算得到主机高度偏差分别为-0.8 mm和+13.5 mm时,3#艉轴承受力分别达到设计值的±20%上限和下限.当主机高度偏差超出临界范围时,将极大地增加轴系校中难度,甚至导致校中失败,此时应先调整主机高度,再进行轴系校中.
4 轴系装调经验验证及理论依据
4.1 轴系装调经验验证
由于在实际安装过程中无法准确测得主机安装高度偏差,只能测量各轴承受力.因此,根据各轴承受力来制定是否调整主机高度的决策是轴系装调过程中需要面对的问题.通过调研得知,针对该船型,船厂技术人员实践经验为:当各中间轴承所受支反力平均值与最靠近主机的艉轴承所受支反力大致相当时,一般不需要调整主机安装高度,适宜直接开展中间轴承的调整工作.该经验知识可表示为
F1+F2+F3=KF4
(7)
式中:F1为1#中间轴承受力;F2为2#中间轴承受力;F3为3#中间轴承受力;F4为3#艉轴承受力;K为经验系数.
为验证该经验的准确性,按3.3的分析条件进行计算得到经验系数K=3.15,与经验描述相近,说明船厂技术人员的装调经验是较为准确的.
4.2 轴系装调经验的理论依据
为建立主机高度偏差与经验系数K之间的关系,找到轴系校中工作难度不大的K值范围,分别计算主机高度偏差从-0.4 mm~+3 mm时的K值,结果见图5.随着主机高度增加,K呈下降趋势.由于3#中间轴承距主机最近,主机高度偏差对其受力影响最大,计算得到不同主机高度偏差时其受力变化趋势见图6,假定3#中间轴承处于设计高度,若其受力在规范允许的偏差内说明主机高度偏差在可接受的范围内,中间轴承调整难度不大.根据3#中间轴承受力的允许偏差计算得到主机高度偏差分别为-0.2 mm和+0.8 mm,K值分别为2.7和3.25,即认为当经验系数K值位于为2.7~3.25区间时,较为适宜进行中间轴承的校中调整,从而在中间轴承的调整难度与主机安装精度要求之间取得较好的平衡.
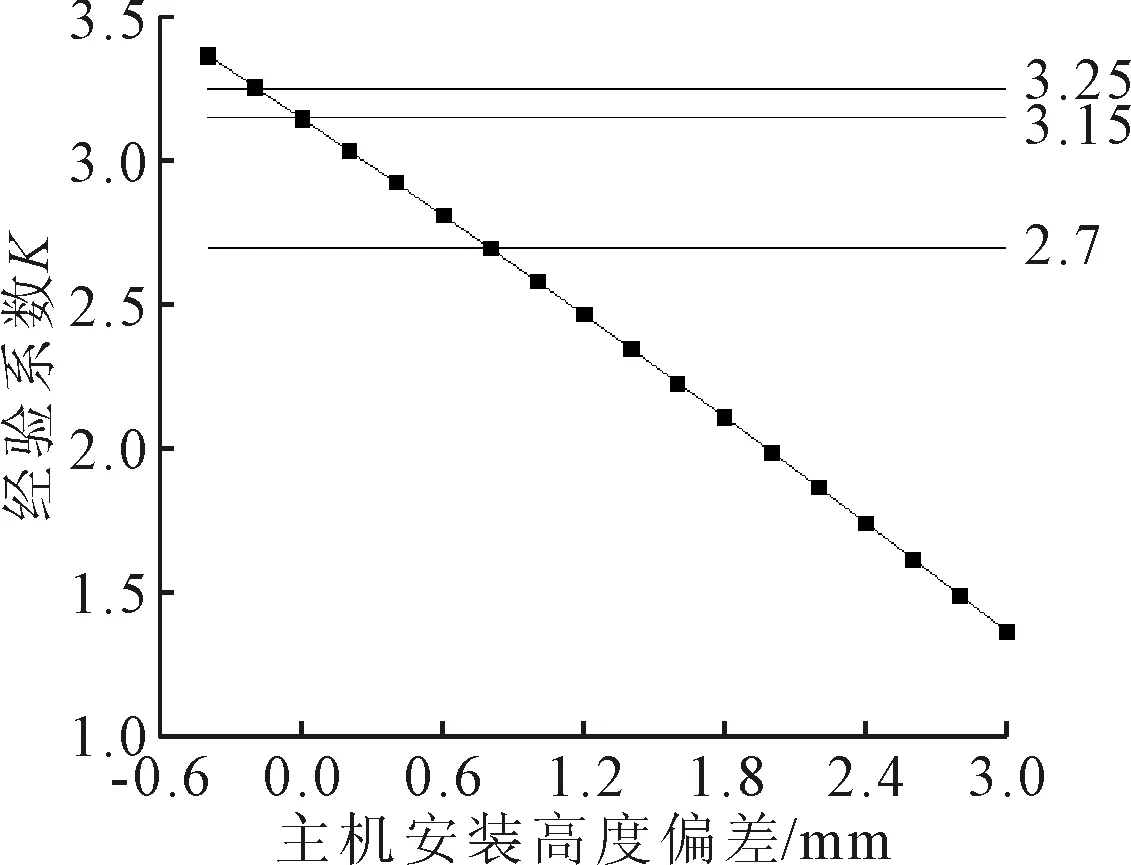
图5 经验系数K值变化曲线
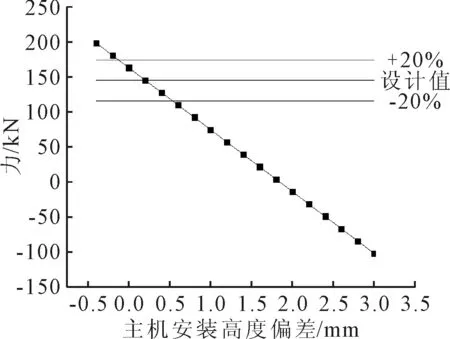
图6 3#中间轴承受力变化曲线
5 结 论
1) 通过轴系力学理论分析可知,主机高度偏差对各轴承受力的影响为线性变化,并且从艏向艉传递时会随距离增大逐渐变小,相邻轴承的影响因子正负交替;以实船为例计算得到各轴承的影响因子.
2) 主机安装高度偏差会压缩轴承变位调整的试错空间,实例计算结果显示主机高度发生+0.1 mm变化时,1#、2#和3#中间轴承试错空间分别压缩了0.8%、0.19%、18.9%;此外过大的主机安装高度偏差将使靠近主机端的艉轴承负荷超出规范要求的范围,此时需要先调整主机高度再进行轴系校中工作.
3) 通过该实例船型轴系装调经验知识的探讨和分析,认为当各中间轴承受力之和是3#艉轴承受力的2.7~3.25倍时,中间轴承调整难度与主机安装精度要求取得较好的平衡,适宜开展中间轴承的校中调整.

