Riks弧长法在压杆非线性屈曲分析中的应用

赵佳音

（中国人民解放军92785部队，辽宁绥中 125200）

0 引言

在船体钢结构中，受压构件一般在其达到极限承载能力前就会丧失稳定性，所以失稳是船体钢结构最为突出的问题之一。受压构件整体失稳形式可以是弯曲、扭转或弯扭。钢构件在轴心压力作用下，弯曲失稳是常见的失稳形式。影响轴心受压构件整体稳定性的主要因素为焊接残余应力、初始弯曲、载荷初偏心及端部约束条件等。实际的轴心受压构件往往会存在上述的一种或多种缺陷，导致构件的极限承载能力降低。

工字钢是工程中常见的钢构件，水面船的龙骨、纵桁与外板连接的位置、潜艇肋骨与外板连接的位置都可认为是工字钢结构。本文利用 ABAQUS对一定截面不同细长比的工字钢构件进行屈曲分析，通过考虑材料非线性、几何非线性并引入初始挠度，得出构件发生弯曲失稳的极限载荷，通过比较不同长细比下的弯曲失稳的临界载荷得出构件载荷位移曲线。

1 模型分析

钢构件的截面尺寸如图1所示。

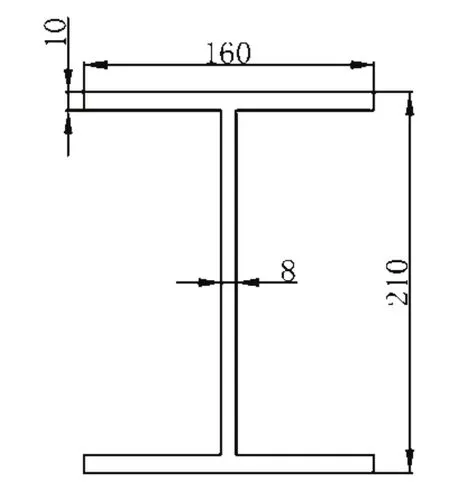
图1 压杆截面尺寸（单位：mm）

构件的材料特性：密度

ρ

=7.85×10t/mm；弹性模量

E

为2.1×10MPa；泊松比

µ

为0.3。其塑性 应力-应变曲线如图2所示。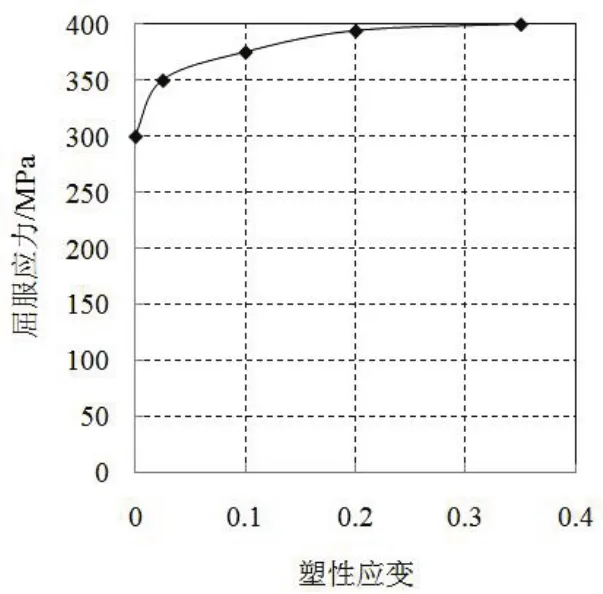

图2 屈服应力与塑性应变的关系

通过计算截面几何特性，截面绕

y

轴的回转半径

i

为3.84×10mm。

长细比取值及杆件长度见表1。

表1 长细比取值及杆件长度

2 非线性屈曲Riks弧长法理论

线性屈曲分析被定义为特征值屈曲预测（eigenvalue buckling prediction），其通常用于评估刚性结构的临界屈曲载荷，也可用于对结构的缺陷敏感性进行前期准备。特征值屈曲分析时所有弹性效应均被忽略，且所有接触均由基础状况确定。如果进一步研究屈曲前材料、几何非线性以及不稳定后屈曲相应，必须进行载荷-位移分析。若要评估结构的最大临界载荷以及屈曲之后的后屈曲状态，需使用Riks弧长法。

对

N

个非线性方程组：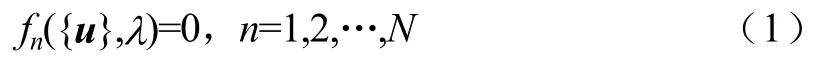

式中：{

u

}为未知位移矢量；

λ

为载荷参数。

该问题通常离散为增量非线性问题：

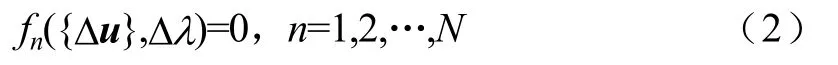
因此问题变为求解：

式中：

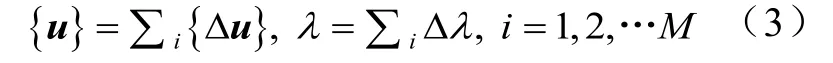
M

为载荷步。式（2）通常用Newton-Raphson法求解。但是，该解法在跨越极限点时无效，这时应用修正的弧长法，约束关系是结构的广义增量位移的“弧长”。也就是说，对当前的广义增量位移矢量{∆

u

}有弧长∆

L

，如图3所示，其中弧长的定义为

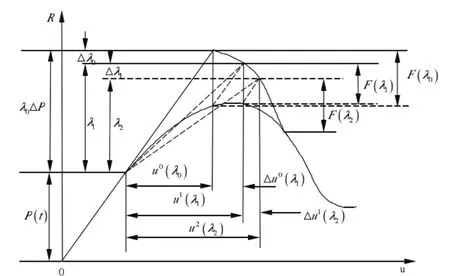
图3 修正的Riks弧长法

在该解法里，仍然应用Newton-Raphson法求解。但在每个增量步里，载荷步的大小随着∆

L

的大小而改变，其中∆

L

由式（1）求得。假设已求得

t

～

t

时刻的位移解，在

t

到

t

+∆

t

增量步中，结构将从稳定平衡状态转向不稳定平衡状态，为使有限元解收敛，在采用修正Newton-Raphson法的同时，增加约束方程的弧长。定义{

u

}为时间间隔

t

+∆

t

内第

i

步迭代后的总增量位移，以

λ

表示载荷增量∆

P

的比例因子，{

u

}随

λ

变化，即{

u

}={

u

(

λ

)}。

3 建模计算过程

建模计算过程以长细比50的构件为例，其余构件建模计算结果与之类似。

3.1 buckle 分析

在buckle分析中创建part模块，创建的模型为三维可变形shell单元，截面参数见图1，构件长度为1 920 mm，定义材料特性及截面属性并将其赋予单元。材料定义为弹塑性，泊松比0.3，屈服强度为300 MPa，弹性模量为210 000 MPa，腹板和自由翼板为shell单元，厚度分别为8和10，如图4所示。

图4 有限元模型

定义边界条件及载荷，边界条件为一端绞支、一端滑动，载荷为1 N/mm的壳边缘载荷（shell edge load），划分网格，创建、提交并运行作业分析，输出前4阶屈曲模态及其特征值，屈曲载荷按

Q

=

λF

计算，如表2所示。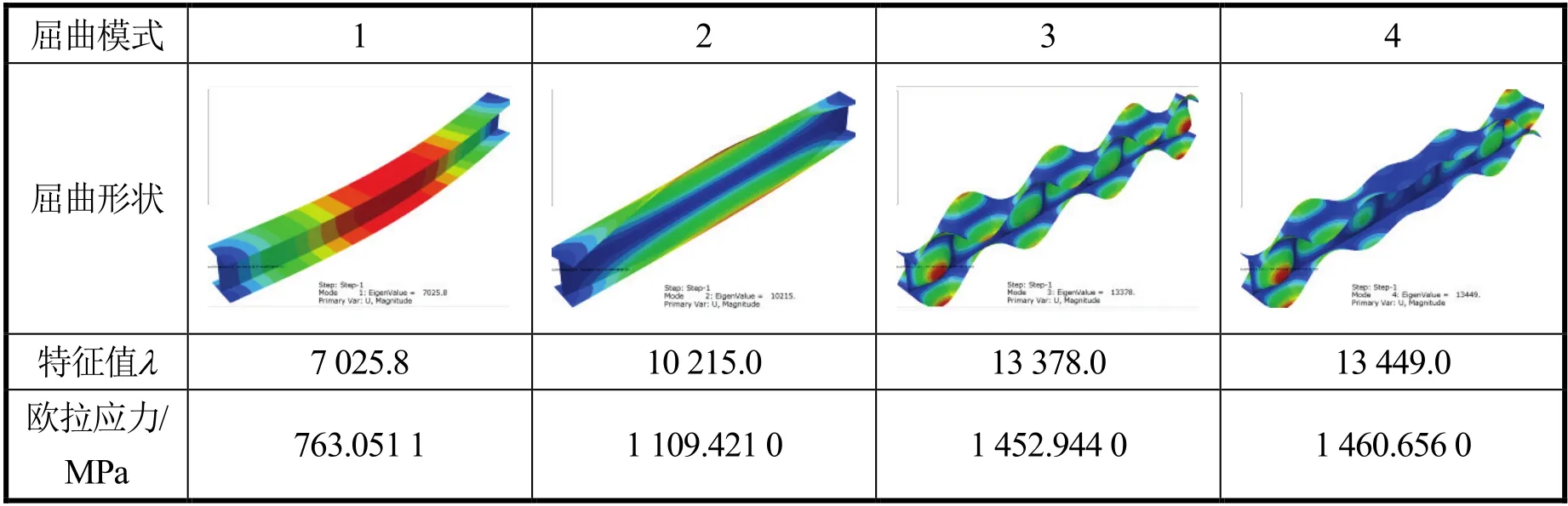

表2 工字钢的4阶屈曲模态

从表2可以看出，3、4阶特征值间隔较小，暗示屈曲临界应力对初始缺陷较为敏感，需进行缺陷敏感性分析。

3.2 Riks 分析

复制模型，替换step，编辑关键字：

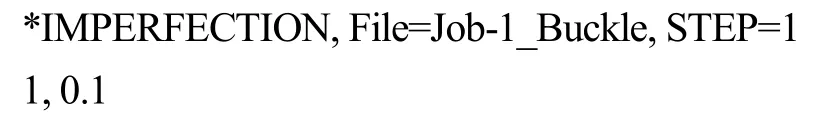
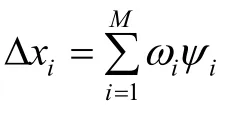
从临界荷载比例系数-弧长曲线（图5）可知，载荷在3 500 N/mm时发生了第一次转折，即第一阶屈曲，远小于线性屈曲分析结果7 025.8 N/mm，说明在初始缺陷存在时，缺陷压杆比完整压杆更容易丧失稳定性。

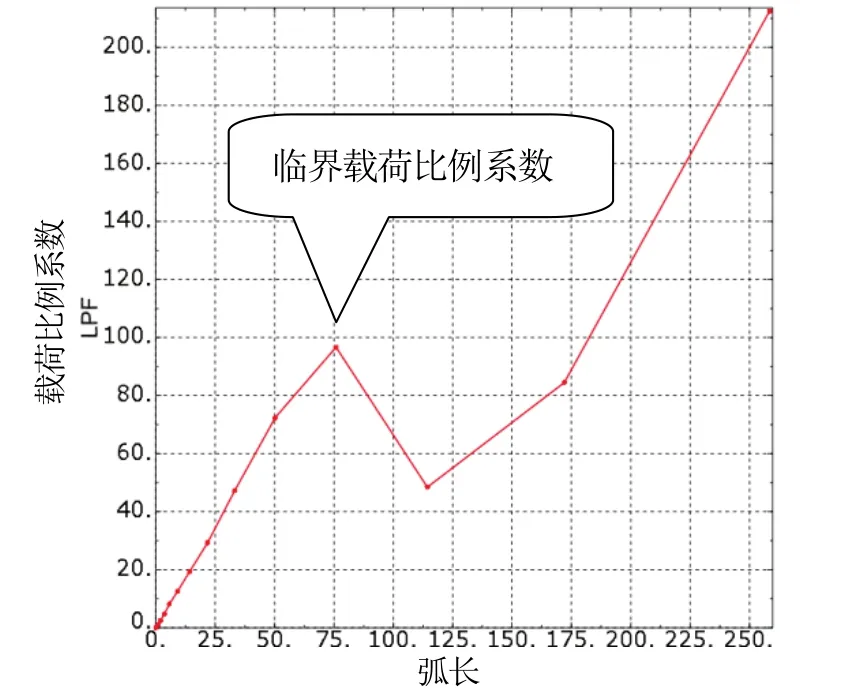
图5 荷载比例系数-弧长曲线

将缺陷因子分别修改为0.15、0.20、0.25、0.30，重复求解得到图6所示的不同缺陷因子时LPF曲线。由图可知，缺陷越大，LPF越小。

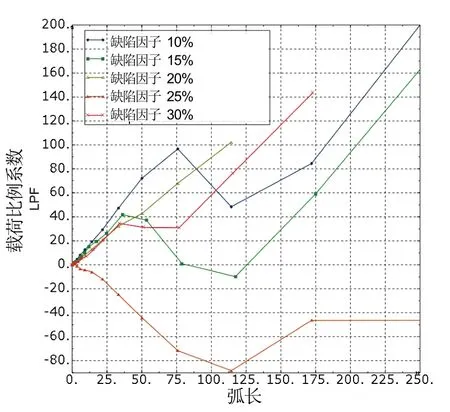
图6 缺陷敏感性

4 结论

本文介绍了Riks弧长法的基本理论，并以工字钢为例，说明了其在压杆非线性后屈曲分析中的应用，根据计算结果，在考虑材料几何非线性时，临界载荷小于线性屈曲载荷，改变缺陷因子，可知缺陷越大，临界载荷比例系数越小。该研究可为薄壁结构单轴压缩下的非线性后屈曲计算提供参考。