从牛顿第二定律到伯努利的F=ma

张鸯丽

(浙江省玉环中学 浙江 台州 317600)

姚珩

(闽南师范大学物理与信息工程学院 福建 漳州 363000)

经典物理学以经典力学为基础，经典力学则以牛顿的外力、第二定律为核心，但牛顿第二定律的数学表达式F=ma并非由牛顿本人所提出，然全世界的中学大学物理教科书都将牛顿第二定律写成F=ma，却都没有指出它的来源，容易给学生或教师误以为它就是牛顿写下来的；并且对该式到底是有关力的定义，还是定律，也模糊不清.那么牛顿第二运动定律的原意是什么？牛顿是如何看待“力”？明白这些问题，对经典力学的理解，教材掌握与教法呈现，将有所帮助.

1 牛顿之前的力概念——力、冲力、惯性力与离心力

对运动问题的探讨最早始于古希腊，他们认为物体下落是重物的本性，因任何变化皆有其目的，重物运动的目的便是朝向世界的中心——地心，此种运动称为自然运动.违反自然运动的称为受迫运动，如石头的上抛，这种运动必须要有推动者给予力，才能发生.因此，从最初运动问题便与力相关，力不是用来讨论物体的形变而生.

他们还认为推动者一定要靠接触，才能将力传递出去，为了要解决抛出石头后不必接触而能继续运动下去的困难，经过很长时间，直到中世纪晚期才有科学家提出：运动的物体可从推动者获取让它能维持运动下去的动力，此动力称为“冲力”.

17世纪初，笛卡尔保留了冲力的观点，并以“运动物体的力”来代表，提出：“每一物体，受其自身的力，将一直维持于相同的状态；一旦它运动后，则将继续运动下去.”运动物体的力已不是来自于推动者的作用，笛卡尔认为物体会携带运动力，是由于最初运动的物体借着碰撞所传递出来的.对他来说，力只有一种，就是运动力，也就是后人所称的惯性力.

惠更斯支持笛卡尔所主张：运动物体总是会沿着直线方向，因此“在圆周上运动的物体总会试着离开圆心，回到原来的直线上”.这种离开圆心的趋势，惠更斯于1659年首次称它为“离心力”.如图1所示，物体自A点运动至B点，则物体在B点上具有回复到C点的趋势，BC长度可代表离心力的大小.

图1 惠更斯提出的离心力的图示

惠更斯在所著《论离心力》一书中，精确地指出离心力大小与速度平方成正比，与半径成反比.虽然他没写下计算式，但此发现则是物理学史上首次以明确的量化形式表示出力概念，对牛顿以及后来的物理学影响很大.此外，在这特别该注意的是：离心力与速度的变化无关，它是以长度、距离或位置的变化来表示.

2 牛顿的离心力与圆周运动

牛顿年轻时依循着惠更斯的思维，将惠更斯的的结果用自己的方法，于1669年在《论圆周运动》一书中写下非常重要的规律[1]：在时间AB中，物体B离开圆心O的离心趋势与离开圆周的距离BC成比例，……有如在无阻力作用时，相对物体在此段时间可自由沿着切线移动，两者所造成的变化距离(如图1)，且

此规律是促成牛顿日后发现万有引力的重要参考，且在此时牛顿是接受惠更斯的做法，以距离或长度来代表力.

3 牛顿的向心力与外力

胡克是首位不依循笛卡尔与惠更斯的离心趋势观点的人，1666年他发表的两篇论文中提出“吸引属性”.并于1679年邀请牛顿参与讨论会，向他提到此种朝向中心的趋势，当时牛顿还回信说从未听过此观点.直到1684年，在回应哈雷的拜访与提问后，写下《论运动》的小册书，第一次提到向心力[1]：

定义1 物体被推动或吸引，朝向中心点的力，称为向心力.

唯有在此概念下，万有引力方有可能被发现.向心力的应用非常广泛，如落体、匀速圆周与椭圆运动全部都是受到向心力的作用.

1686年牛顿在其巨著《原理》中，才首次出现除“惯性力”与“向心力”以外的“力”[2]：

定义4 外力是施加在物体上，用来改变其静止或等速运动状态的作用.

由此叙述可知，在牛顿心中，力不是物体的质量与加速度的乘积，不是物体的重量，不是推力、拉力或弹力，它是与运动状态有关的概念，是一种造成物体运动有所变化的影响或效果，它更是揭开自然现象的关键概念.

4 牛顿第二运动定律呈现于1686年

4.1 不使用第二定律仍可得到面积律与距离平方反比律

1684年，牛顿只有向心力概念，尚无外力一词，也没有第二定律，但他在当年《论运动》著作里却可得到以下重要结果[1]：

定理1：在向心力作用下，运动物体与力心连线描绘出的面积正比于时间.

此定理意谓开普勒面积定律是因行星受到向心力作用所致，它也是日后《原理》中的第一个定理，其重要性不可轻忽.牛顿此时是如何在不知道第二运动定律之下，发现出来此重要规则？他主要是利用了伽利略在平面运动上位移合成的想法与主张：

力的作用 = 在给定时间所产生的位移或速度

以此来表示力作用的效果，由此提出了重要的预备定理(图2)[1].

预备定理1：二力(如AB,AC)合成在某段时间作用在物体上的结果为一平行四边形的对角线(AD)，其两边为各分力在同一时间下的作用.

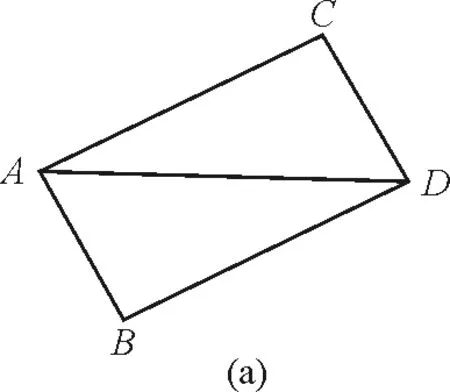
将此定理运用在受向心力作用的平面运动物体上时，最初惯性力AB作用下所造成的物体位移Bc(图3)，与在B处同时受到向心力(或脉冲力impulse)F作用造成的效果Bb，二力的合成作用为对角线BC，此时cC//BS，故面积△SAB=△SBc=△SBC. 而证得定理1.

图3 惯性力与向心力合成的作用结果

他接着使用相同的合成方法，而非第二运动定律，在《论运动》中证出:做椭圆运动物体所受之向心力与物体至焦点的距离平方成反比.由此可看出，牛顿在此时的力概念只有两个：惯性力与向心力，尚无外力的观点，且他还不清楚日后的第二运动定律，也不明白物体做平面运动的加速度是何意，又该如何描述，但他此时已快得到行星运动所受的万有引力形式了.

4.2 第二定律的提出与使用

两年后，牛顿做了很大的改变，他引入了第二个新概念——外力，如前第3节的定义4所述，并在《原理》中写下他划时代的第二运动定律[2]：

定律Ⅱ公理Ⅱ：运动量的变化与外加的动力(或外力)成比例，且运动量的变化是沿着外力的直线方向上.

其中“运动量”也就是现在所说的动量，而“运动量的变化”不是惠更斯于1659年所言回到惯性运动上的位移.反之，它是从原初的动量(也可视为速度或位移)，指向后来的动量.亦即在第二定律里出现了两个前所未有的概念——“动量变化”与“外力”，这是其他物理学家，甚至之前的牛顿本人，从未想过或使用过的方法.

牛顿在与友人的信中曾以简图4表示：物体做曲线运动，从A运动到b，则运动量的变化为ab，其大小与作用“在原来A处”的外力成正比，且方向相同，这就是第二定律的全部意义.其内涵却相当新颖，完全创新，这种“动量或运动状态的改变，以及如何将它量化”是牛顿全新的观点，它使用此定律推导出《原理》一书中许多有用结果，也推导出:若物体受到与距离平方成反比的外力，物体将做椭圆或双曲线运动.从此，第二定律所揭示分析运动的方法，对日后物理学家探讨运动的思维，起了巨大的指导作用与贡献.

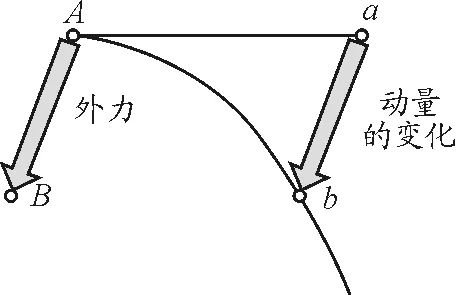
图4 牛顿第二定律重要示意图

牛顿自此已倾向于不用惯性力，他认为物体由A到a是初动量或初状态，而不说是受到惯性力作用.他也不用二力——惯性力与向心力的合成，而是反过来，由动量变化或加速度，去寻找外力的数学形式.

现以《原理》中定理1的论证内容，来对比《论运动》中定理1的证明方法(如4.1节与图3所述)，可初步体会1686年时牛顿是如何引用他的第二运动定律，与处理物体动量变化的方法:

定理1 做环绕运动的物体，其指向稳定力心的直线所掠过的面积位于同一平面上，且正比于时间.

证明:在不受外力作用下，于相同时间间隔下，物体在A与B处的动量，可以长度AB与Bc表示，且AB=Bc.若在B处，物体受到外力作用，且指向力心S，造成物体在B点的动量为BC，物体的动量变化为cC，由第二定律，cC//BS，故面积△SBc=△SBC(同底同高)，如图5，而得证.

图5 以第二运动定律证明面积定律

第二定律最大的特色是在处理非直线的平面运动，如圆、抛物线或椭圆.对这些运动,在牛顿之前无人曾提及物体动量(或速度)变化的明确意义. 一般人或许不难理解直线运动上的速度变化或加速度，因两者都会在同一直线上，但做平面运动的加速度为何是牛顿所规定的方式：由初速度的端点指向末速度的端点，这是牛顿独创的观点，是相当关键与困难的一步.教学者宜谨慎对待，并予以强调.

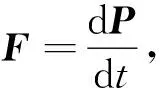
命题11:做椭圆运动的物体必受到至交点距离平方反比的外力作用.

5 伯努利首次写下f=ma

《原理》一书使用了大量几何图形的论证方式，一般人不易读懂.瑞士数学家伯努利于1736年发表了《关于光如何传播的物理和几何研究》，他在书中描述了光传播的惊人速度，也确信大自然中存在着高速运动的物体，并尝试着解释光传播的相关现象.他认为力是一个决定性因素，力或多或少可移动一些物体，并且在作用了一段时间后，都会在所作用的物体上产生一个加速度.他写下如图6所示一段话.[3]

图6 伯努利第一次写下f=ma

原意为:为求更好的了解，只需要确信所解释的动力实际上是物体的质量和所施予加速度的组合；它意味着通过命名动力f，物体质量m和加速度a，就可以得到f=ma.

这便是历史上第一次清楚以f=ma的形式来表示牛顿第二定律的数学式，之后它也成为世上普遍使用的写法. 它大大简化了牛顿的几何作法，带来许多方便，伯努利也使用第二定律的代数方式开启探讨流体运动现象.由于它简单，容易操作，在教学上有不少方便，学生们也可朗朗上口，这是伯努利很大的贡献.

6 讨论与结论

每位物理教师都非常熟悉的牛顿第二定律f=ma，并非只是以“力是产生加速度的原因”或“物体所产生的加速度与外力成正比”，就可呈现出其深刻意义.回顾与明白上述的发展过程，可以更丰富教师的教学内涵:

(1)力——何谓力？是弹力、摩擦力或是一种变形？牛顿并未如此说，他最初只有惯性力与向心力的概念，最后才加上外力，他所谓的“力”是为了改变物体运动状态的作用，该如何以数值或几何方式「量化」外力，是他的首要工作.

(2)动量变化或加速度——在直线上运动的加速度就是速度之差，但是平面运动的加速度如何求得？牛顿之前无人知道，也没人如此去描述.牛顿首先规定平面上的加速度是由初速端指向末速端，开启了全新的论证方式.

(3)目的——提出f=ma的目的就是牛顿所言“从运动的现象去研究自然界中的力，然后从这些力去说明其他自然现象”[2]，当f=ma中的f未知时，物理学家便试着由运动轨迹中的加速度去寻找力的数学形式.相对地，若f已知，则可由第二定律，描绘出运动轨迹.

牛顿第二运动定律是经典力学的基础，了解它背后形成过程的曲折与创新，对牛顿力学的结构可以有更清晰的体会与掌握.力不是推力与拉力的延伸，它是为了要描述行星与落体运动现象的一致性而被提出的；其中如何描述在平面上运动物体的加速度，则是牛顿很关键的突破；后来的伯努利以f=ma把牛顿的物理精华浓缩成为常人能解的一种标准范式.