在大学物理教学中培养学生的批判性思维能力*
——浅析开放性提问的作用

2021-03-04 05:42张义冯兴汪建殷鹏飞孙希媛王开明

物理通报 2021年3期

张义冯兴汪建殷鹏飞孙希媛王开明

(四川农业大学理学院应用物理系四川雅安 625014)

在互联网时代，知识的获取已非常便捷，大学的任务已逐渐从知识的传授向能力的培养方向发展．教育部在2010年颁布的《高等学校应用物理学本科指导性专业规范》中首次强调要培养学生敢于和善于提出问题的能力，具有独立思考和批判精神，创新意识和创新思维[1]．因此好的教师应该是一个激励者，善于激活学生的思维和大脑，激励学生主动质疑．那么如何激发出学生的问题呢？有专家将课堂问答分为以学为中心和以教为中心的课堂问答过程[2]．传统的以教为中心的课堂问答中，教学内容是固定的，不仅学生无疑问，教师也无，教师只是教材内容的忠实传递者．在这个过程中，学生只是被动地思考问题，思想和情绪很平淡，因此很难激发学生主动提出问题．而在以学为中心的课堂问答过程中教学内容不仅仅是书本上已有的知识点，更是开放性的、探索性的、跟生活紧密联系的问题．学生在遇到这些开放性问题时会感到惊讶、困惑、好奇或兴奋，而往往这样更能启迪思维，激发智力．

笔者从开放性提问的角度出发，以大学物理课程中的力学和光学内容为例，通过结合科学发展史、挖掘习题深度、设计演示实验、工程案例教学4种方式，讨论了如何挖掘开放性问题，激发学生的疑问，培养学生的批判性思维能力．

1 结合科学发展史

科学发展的过程就是批判性的、不断接近真理事实的过程，质疑精神对于自然科学的发展至为重要．例如，随着物理理论的发展，人们发现几何光学中光的直线传播定律只有在一定前提下才成立[3]．因此可在课堂上沿着光的传播规律的认识过程依次提出问题，首先问：光在均匀媒质里一定沿直线传播吗？我们知道光的直线传播定律必须在光波波长远小于障碍物尺寸的前提下才能成立，否则会发生衍射现象，光会传播到几何阴影中去．由于中学时代有学生已经了解了光的衍射，因此部分学生能够回答出衍射现象不满足直线传播定律的反例．但随着近代爱因斯坦相对论的创立，光的传播规律又受到了更深刻的撼动，根据爱因斯坦广义相对论，质量非常大的物体会导致周围的时空弯曲，并使得光线发生偏折．这个预言也在1919年通过了实验验证：实验人员观测了视线掠过太阳附近所看到的恒星位置，证明太阳引力导致恒星光线偏折了1.61弧秒，偏折角度与爱因斯坦所作的预言非常接近[4]．因此可知即使光线处于真空中并且障碍物尺寸远大于光波波长的情况下，也可能出现光不沿直线传播的现象．在此基础上可进一步提出问题：满足障碍物尺寸远大于光波波长后，直线传播定律就一定成立吗？此时学生更加好奇而疑惑，能够给出答案的学生已经不多了．但是通过以上结合光学发展史的开放性提问过程，会使学生意识到严谨的实验验证和逻辑推理对于科学发展的重要性，对独立思考和批判性思维有一定的启发作用．

2 挖掘习题深度

在课程习题的讲授中，教师如果给出正确的解题步骤，固然能起到巩固知识点的作用，但这样学生只被动的接受，缺少思维的碰撞过程．因此，在习题的讲授中教师可挖掘题目的深度，设计一些开放性问题，让学生存疑求证．下面以一道刚体力学题为例予以说明：如图1所示，两人各执均匀杆(重G，处于水平静止状态)的一端．当左侧人突然放手时，右侧人手上用力变为多少？

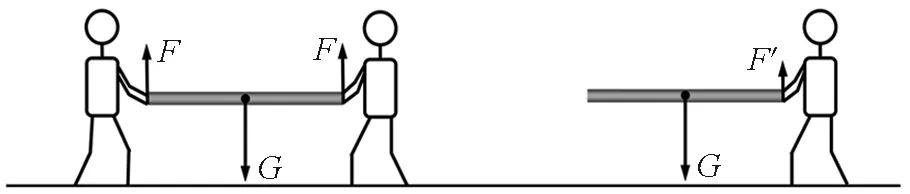
图1 两人执杆习题示意图

可先给出一种可能性：“原来两人执杆，后仅一人执杆，右侧执杆人用力会变大？”这看似正确的逻辑推论对不对呢？大部分学生通过角动量定律的学习后可得到如下解题过程：设左侧人放手后杆的加速度大小为a，角加速度为β，右侧人在左侧人放手前后用力分别为F和F′，基于牛顿第三运动定律和角动量定律建立以下方程

G-F′=ma

a=0.5Lβ

最后可得F′为0.25G，而两人执杆时每人用力F为0.5G．可以发现仅右侧一人执杆时，他用力反而变小了，与假想的结论完全相反，这样的结果会让学生感到惊讶、产生疑问，会产生进一步探究的兴趣．

接下来教师可引导学生去反思背后的物理原因，提出问题：相对于两人执杆，一人执杆时为什么用力反而会变小？用力大小与两人执杆的位置有没有关系？如果改变其中一人的位置，剩下的人用力还是变小吗？这时的问题就比较深入而有趣了，学生也想进一步去研究执杆位置对用力大小的影响．部分学生通过计算可得出以下结果：以改变右侧人位置为例，以杆中央为原点建立如图2所示的坐标系.

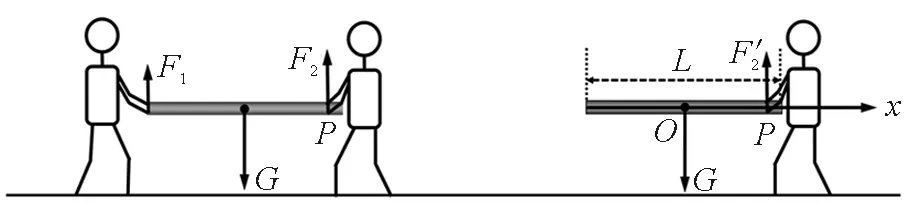
图2 研究执杆位置对力的影响

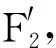
a=xβ

最后可得到

而通过力矩平衡可得放手前右侧人的用力为

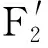
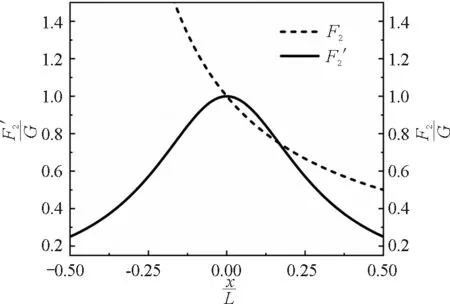
图3 放手前后右侧人用力F2与随x的变化关系

3 设计演示实验

物理是一门以实验为基础的科学，如果课堂上只有理论教学，学生难免感到平淡，因此教师可设计演示实验并展开提问，将理论和实践联系起来．例如伯努利方程的学习中，可设计出如图4所示的两种装置，与学生讨论．对于图4(a)中的空吸装置，根据伯努利方程可知，由于出口处的气体流速小于细管处的流速，因此细管处的压强要小于出口处的大气压，最终导致液面上升．授课教师可在学习伯努利方程前给出该装置图，并提出这样一个问题：“在推动活塞的过程中，由于气体被推动向前和向下，液面应该会被气体压的下降？”由于缺乏流体力学相关知识，学生一般都认同这种现象会发生．此时教师可拿出图4(b)所示玻璃管，将竖直管插入水中，并从左向右对水平管吹气，可发现竖直管中的水面竟然会上升．接着，伯努利方程学习结束后又可给出图4(c)装置，提出问题：如果管径是均匀的，液面还会上升吗？此时较多学生会有以下推论：管径没变化，出口处的气体流速和中间分支管处的流速相同，分支管处的压强等于出口处的大气压，因此液面高度不变．事实上，最终通过图4(d)所示的T形管实验可以发现液面是下降的．这是由于空气并非理想流体，是可被压缩的，而伯努利方程仅适用于理想流体，因此管内气体由于被压缩导致压强要略大于大气压，从而导致液面下降．相反，如果是从水平管右边吸气，会导致气体膨胀，压强变小，液面上升．通过该演示实验的讨论，学生能够对伯努利方程和理想流体的概念有更深刻的理解，并会发现，许多看似合理的逻辑竟然不对，只有通过亲自实验才能判断真伪．

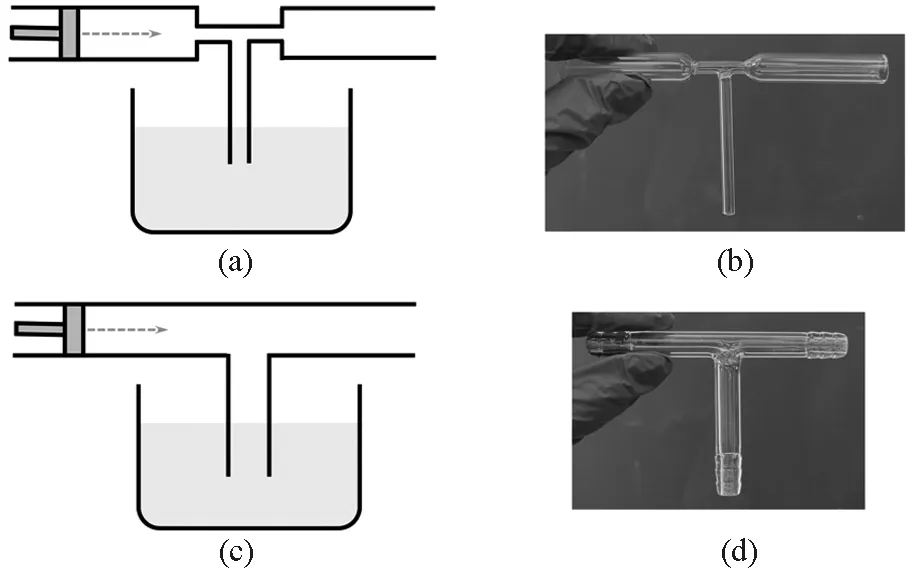
图4 两个演示实验装置

4 加强工程案例教学

古往今来，人类创造了许多伟大的科技成就和工程发明，如蒸汽机、人造卫星、手机等，而这些科技发明中的工程元件结构，往往经历了长期的实践和改进才最终成型．因此针对某个工程元件的结构设计加以讨论，也是锻炼批判性思维很好的途径．例如，在刚体力学的内容中可给出发动机中的曲柄连杆机构图(图5)，就活塞的形状进行讨论．以图中活塞为研究对象，进行受力分析：活塞除了受到向下的气体压力F外，还受到连杆产生的斜向左上的压力Fl，和左侧气缸壁向右的侧压力Fc．在侧压力Fc作用下，活塞截面会被挤压变形成椭圆状，进而可能造成活塞卡死或局部磨损过大．实际工程中为了解决这个问题，往往预先将活塞加工成椭圆柱形，椭圆面的长轴与左右侧壁垂直，以抵消掉挤压造成的变形．另外由于发动机工作时活塞顶部温度高，热膨胀更大，因此为了防止活塞卡死，其顶部直径往往要小些，由顶部向下直径是逐渐增加的，一般呈锥形或阶梯型[5]．针对这些工程知识，可以对学生提出如下问题：发动机气缸内部为圆柱形，那其中活塞也是圆柱状吗？如果考虑到受力情况和热胀冷缩呢？通过以上力热学分析，学生会发现原来理所当然的结论却在实际应用时因为要考虑诸多因素而大相径庭，意识到质疑的重要性，并对实际工程应用有所了解．

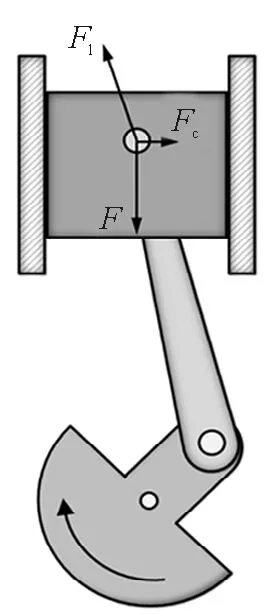
图5 曲柄连杆机构

5 结束语