多项分数阶非线性微分方程的数值方法
乔 智,赵维加,黄健飞
(1. 扬州大学数学科学学院,江苏扬州225002; 2. 青岛大学数学与统计学院,山东青岛266071)
分数阶微积分[1]是数学的一个重要的分支,距今已经有300多年的历史。近年来,分数阶微积分算子的非局部性使得分数阶微分方程在建模复杂动力系统和材料方面的应用越来越广泛,比如各种黏弹性材料[2]、反常扩散[3-4]、分形理论[5]、化学和生物化学[6]。与整数阶微分方程相比,分数阶微分方程的物理意义更清晰,模型更简单;但是,精确求解分数阶微分方程通常比较困难。对于一些非线性分数阶问题,甚至不可能获得其精确解,因此,研究者广泛设计和使用数值方法来求解分数阶微分方程。
目前,许多论文研究了分数阶常微分方程数值方法。早在1997年,Diethelm[7]对一类分数阶常微分方程构造了基于求积公式的隐格式,并给出了严格的误差分析。这是公认的分数阶微分方程数值方法领域比较早的工作之一。随后,Edwards等[8]研究了线性多项分数阶微分方程的数值解,但是没有考虑非线性多项分数阶微分方程的情形。El-Mesiry等[9]给出了求解非线性多项分数(任意)阶微分方程的数值格式,只通过数值实验来验证格式的计算效果。Kumar等[10]采用积分方程的思想,针对一类分数阶常微分方程设计了一个高阶格式,数值实验表明该方法有较高的精度。Lin等[11]采用生成函数法推导出求解分数阶常微分方程的高阶近似,证明了这些方法的可解性、收敛性和稳定性,但是这些方法只能用来求解含有一个分数阶导数项的方程。Ford等[12]考虑了多项分数阶微分方程近似解的基于系统的分解方法,但是只考虑了各分数阶指标单调递增的情况。Huang等[13]详细地证明了文献[10]中所给出的数值方法至少具有3阶精度。此外,关于分数阶偏微分方程数值方法的研究,可以参考文献[14-18]。
本文中研究一类多项分数阶非线性常微分方程初值问题的数值方法;为了降低对解函数正则性的要求[19],利用Riemann-Liouville积分算子,将该类多项分数阶非线性常微分方程化为与之等价的积分方程;为了避免求解非线性方程和保证数值方法的稳定性,分别利用复化右矩形公式和左矩形公式来离散积分方程左边和右边的Riemann-Liouville积分,获得一个显式的数值方法;分别考虑2种不同形式的多项分数阶非线性微分方程,并证明2种不同问题数值方法的收敛性和稳定性。
1 情况1下数值方法的构造
考虑情况1,即0<α1<α2<…<αM<1条件下,带有初值条件u(0)=u0的多项分数阶非线性微分方程
(1)
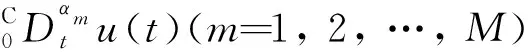
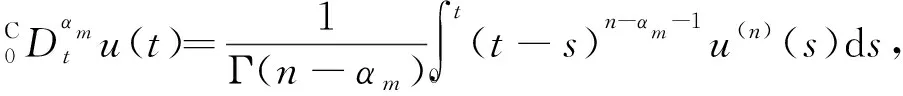
n-1≤αm≤n,
αm(m=1,2,…,M)为阶数,n为正整数;u(0)为0时刻的函数值,u0为常数;f(t,u)在区间Ω上连续,其中Ω=[0,T]×,f关于第2个自变量满足Lipschitz条件,即
|f(t,u1)-f(t,u2)|≤L|u1-u2| ,
其中Lipschitz常数L>0。
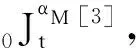
则有
(2)
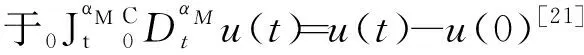
因此式(2)可化为
(3)
对于T≤1,假设f[t,u(t)]在[0,T]上一阶连续,分别运用复化乘积右矩形公式和左矩形公式对式(3)左边和右边的Riemann-Liouville积分进行逼近,可得
(4)
成立,其中
在式(4)中,移去截断误差O(h),用数值解un代替精确解u(tn),则有
(5)
其中
由此,式(3)的数值方法为
(6)
对于T≥1,对式(1)作变量替换,令sT=t,则0 (7) 与T≤1的情形相似,式(7)可离散为 (8) 在式(8)中,移去截断误差O(h),则数值方法变为 讨论数值方法式(6)、(9)在情况1下的收敛性与稳定性。在证明过程中用到Gronwall不等式[6]。 引理1设C1>0且独立于h>0,C2为正常数,且满足不等式 j=0,1,…,n-1,nh≤T, 其中0<α<1,则有 |zn|≤C2Eα[C1Γ(α)Tα],nh≤T, 其中Eα为Mittag-Leffler函数,定义为 下面给出收敛性分析。 定理1假设f[t,u(t)]在区间[0,T]上一阶连续,对充分小的时间步长h,式(1)的数值方法式(6)、(9)在情况1下的收敛阶数为1,即|en|=|u(tn)-un|≤Ch,n=1,2,…,N,其中C为与离散化参数无关的常数,并且C可能有不同的值。 证明: 由于式(6)、(9)的收敛性分析类似,因此只证明式(6)的收敛性。f[t,u(t)]在区间[0,T]上一阶连续,根据中值定理,存在Lk,使得 f[tk,u(tk)]-f(tk,uk)=Lk[u(tk)-uk]=Lkek, k=1,2,…,N。 成立,其中ek=u(tk)-uk。f(t,u)满足Lipschitz条件,则|Lk|≤L。对于0<β<1,1≤k≤n-1,有 (10) 和 (11) 式(10)减式(11),并进行简单放缩,有 由于tn-k=h(n-k),因此 ChαM-α1|en|+Ch。 考虑到tn-k∈ (0,1],有 CMhαM-αM-1|en|+Ch≤ CMhαM-αM-1|en|+Ch, 因此 (1-CMhαM-αM-1)|en|≤ 当h充分小时,由引理1,可得 定理1证毕。 利用定理1的证明思想,可以建立数值方法式(6)、(9)的稳定性结果。 定理2对于充分小的h,式(1)的数值方法式(6)、(9)是无条件稳定的,即 由于稳定性分析与收敛性分析类似,因此定理2证明略。 考虑式(1),初值条件为u(0)=u0,u′(0)=a且0<α1<α2<…<αM-1<1<αM<2,αM-αM-1>1。应用情况1中的离散化方法,可以得到 由此可知,在情况2条件下的数值方法为 (12) 下面给出数值方法式(12)的收敛性和稳定性分析。 定理3在式(1)中,假设f[t,u(t)]在区间[0,T]上一阶连续,且对充分小的h,在情况2下,数值方法式(12)的收敛阶数为1,即 |en|=|u(tn)-un|≤Ch,n=1,2,…,N。 证明: 与情况1相似,有 由于αM-αM-1-1>0,…,αM-α1-1>0,因此 对于充分小的h,根据Gronwall不等式,有 |en|≤Ch。 定理3证毕。 定理4对于充分小的h,求解式(1)的数值方法式(10)是无条件稳定的,即 证明: 与情况1的稳定性分析相似,等式 由于αM-αM -1-1>0,…,αM-α1-1>0,因此 对于充分小的h,根据Gronwall不等式,有 |εn|≤Cη。 定理4证毕。 例1分别在T=1 s和T=2 s时考虑初值条件为u(0)=0的带有2项Caputo导数的方程 其中0<α1<α2<1。该方程的精确解为u(t)=tα2+1。注意到方程右端的光滑性满足定理1的条件。图1所示为T=1 s且h=0.025 s时,精确解和数值解的比较。从图中可以看出,数值解与精确解非常一致。表1所示为当T=1 s,α1=0.1,α2=0.3,α1=0.8,α2=0.9且不同时间步长时式(6)的误差和收敛阶。表2所示为当T=2 s,α1=0.2,α2=0.4,α1=0.6,α2=0.8且不同时间步长时式(9)的误差和收敛阶。从表1、2中可以看出,随着步长h的减小,数值方法的误差也减小,收敛阶约数为1。 α1、α2—收敛阶数; t—时间; u(t)—关于t的函数。图1 时间T=1 s, α1=0.1,α2=0.3,α1=0.8, α2=0.9时方程的数值解与精确解 表1 时间T=1 s, α1=0.1, α2=0.3,α1=0.8, α2=0.9且不同时间步长时式(6)的误差和收敛阶数 表2 时间T=2 s,α1=0.2,α2=0.4,α1=0.6,α2=0.8且不同时间步长时式(9)的误差和收敛阶数 例2分别在T=1 s和T=2 s时,考虑初值条件为u(0)=0的带有5项Caputo导数的方程 其中0<α1<α2<α3<α4<α5<1。该方程的精确解为u(t)=tα5+1。图2所示为当T=2 s,h=0.05 s,α1=0.1,α2=0.3,α3=0.5,α4=0.7,α5=0.9时方程的精确解和数值解。从图中可以看出,数值解与精确解非常吻合。表3所示为T=1 s,α1=0.1,α2=0.3,α3=0.4,α4=0.8,α5=0.9且不同步长时式(6)的误差和收敛阶数。表4所示为T=2 s,α1=0.1,α2=0.3,α3=0.5,α4=0.7,α5=0.9且不同步长时式(9)的误差和收敛阶数。从表3、4中可以看出,当h减小到之前的1/2时,误差也减小到之前的1/2,收敛阶约数为1。 α1、α2、α3、α4、α5—收敛阶数; t—时间; u(t)—关于t的函数。图2 时间T=2 s,α1=0.1,α2=0.3,α3=0.5,α4=0.7,α5=0.9时方程的数值解与精确解 表3 时间T=1 s,α1=0.1,α2=0.3,α3=0.4,α4=0.8,α5=0.9且不同时间步长时式(6)的误差和收敛阶数 表4 时间T=2 s,α1=0.1,α2=0.3,α3=0.5,α4=0.7,α5=0.9且不同时间步长时式(9)的误差和收敛阶数 例3 当T=2 s时,考虑初值条件为u(0)=0,u′(0)=0的带有3项Caputo导数的方程 其中0<α1<α2<1<α3<2。该问题的精确解为u(t)=tα1+2。表5所示为当T=2 s,α1=0.3,α2=0.7 ,α3=1.5时式(12)的误差和收敛阶数。从表中可以看出,当h减小时,误差也随之减小,并且收敛阶数趋近于1。 表5 时间T=2 s,α1=0.3,α2=0.7,α3=1.5且不同步长时式(10)的误差和收敛阶数 本文中基于等价的积分方程,对具有不同初值条件的多项分数阶非线性微分方程,构造了具有一阶精度的显式数值方法。针对2个不同的初值问题,证明了数值方法的收敛性和稳定性。最后,通过计算带有2、5、3项Caputo分数阶导数的数值算例,验证了理论分析结果的正确性。在以后的研究中,将尝试把本文中的数值方法扩展到多项时间分数阶偏微分方程的数值求解。2 情况1下数值方法的收敛性与稳定性

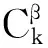

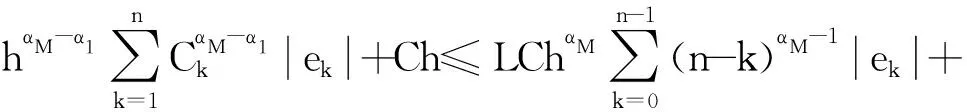

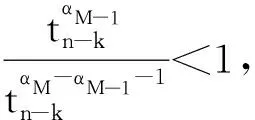
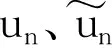
3 情况2下数值方法的构造以及收敛性与稳定性
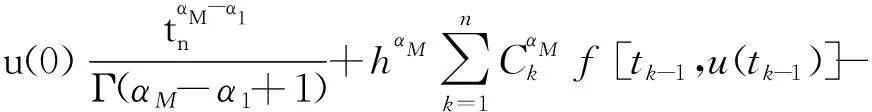

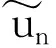
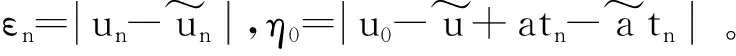
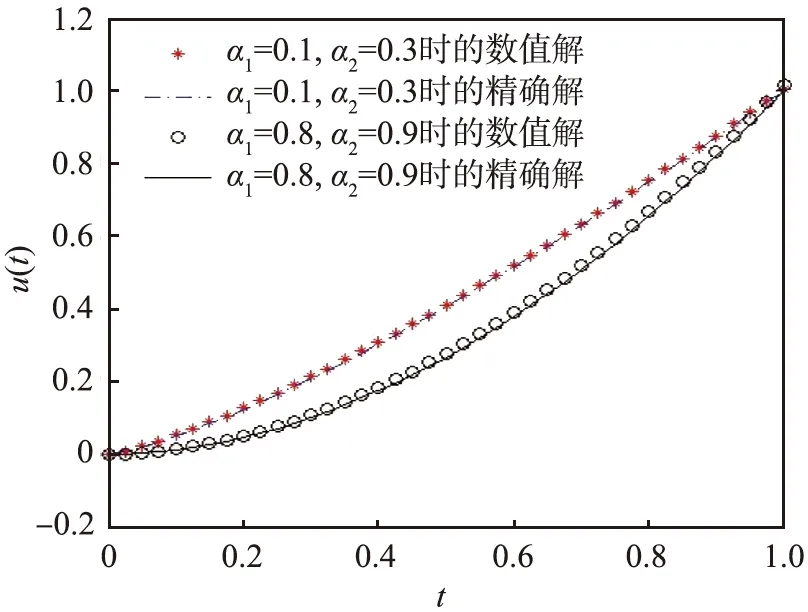
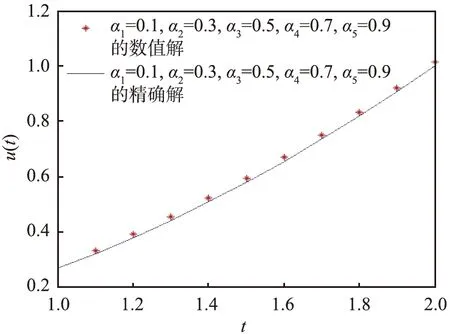
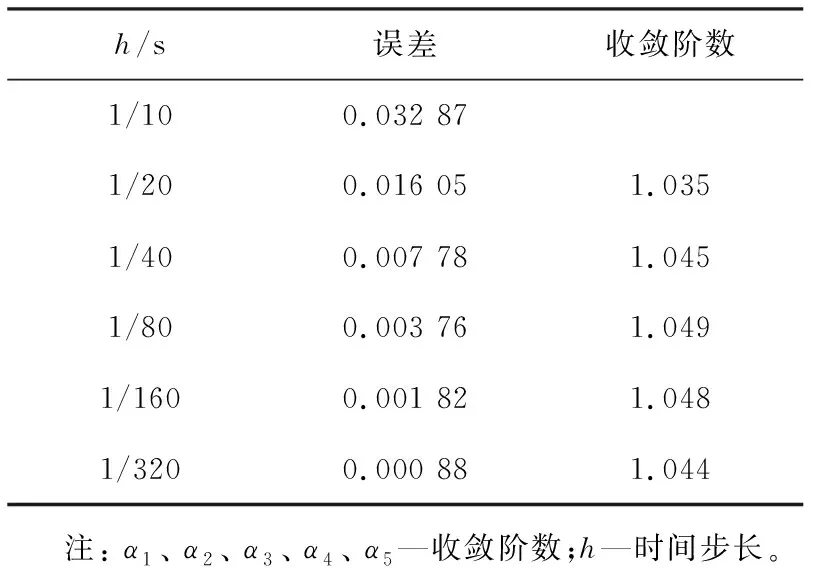
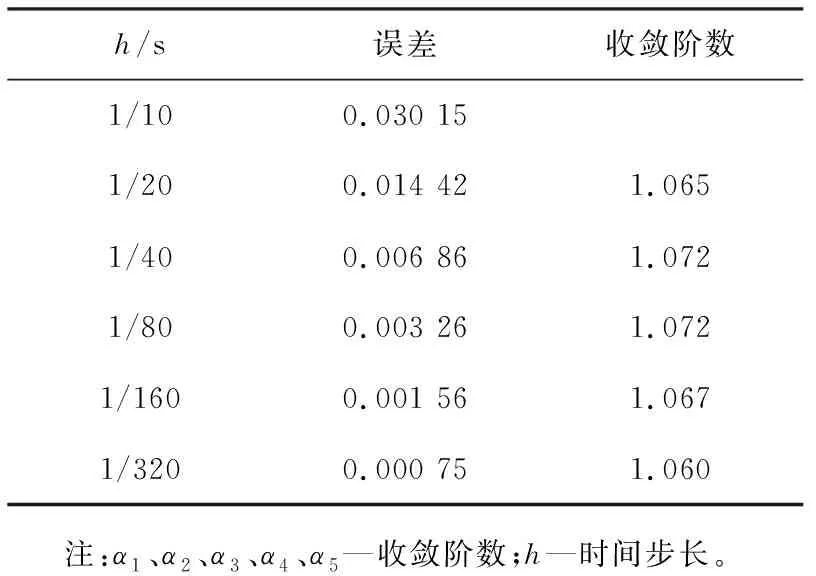
4 数值实验





5 结论

