建筑施工高风险行为高灵敏度自适应监测技术

徐建中，陈潜心

(哈尔滨工程大学经济管理学院，黑龙江哈尔滨150001)

自2009年以来，我国建筑业增加值占国内生产总值比例始终保持在6.5%以上，是国民经济的支柱产业，并占主体地位，到2016年，建筑行业全年国内生产总值已经达到744 127亿元，比上年增长6.70%[1]。在此背景下，2016年底，建筑业从业人数达到5 185.24万，占全社会就业人员总数的6.68%，比上年提高0.10%，占比创新高；然而，建筑行业作为一种高危行业，其安全生产低主动性行为始终存在隐患。我国建筑施工不断向深基础、高楼层、复杂工程发展，加上周期长、劳动强度高等特点，各类建筑安全事故接连不断，每年都有成千上万人在建筑施工过程中受伤或者死亡，造成直接经济损失超过百亿，因此安全生产低主动性行为造成了建筑施工的高风险性，也严重制约了我国建筑行业的持续健康发展[2]。

在上述背景下，监测建筑施工存在的风险具有重要的现实意义。当前建筑施工风险监测主要有3种方法，即基于支持向量机的风险监测、基于模糊综合评价的风险监测以及基于灰度关联的风险监测。虽然这3种风险监测方法较常见，但是，随着建筑施工风险不可控因素的增多，监测方法的自适应性逐渐衰减，导致监测方法的灵敏度和匹配度下降，从而无法准确预判建筑施工行为可能存在的风险[3]。

针对上述问题，本文中提出一种基于结构方程的建筑施工高风险行为自适应监测方法，构建风险监测结构方程模型与校验模型，将模型转换为结构方程[4]，以改善建筑施工高风险行为自适应监测方法的有效性和自适应性。

1 施工风险自适应监测技术

自适应监测以结构模型为基础，监测建筑施工高风险行为，自适应监测过程如下。

1)模型构建。主要工作为收集相关风险数据，筛选收集到的数据，缩减其规模，并制定风险清单，以此构建初级结构模型[5]。

2)校验构建的初级结构模型。①模型识别：识别模型身份，保证系统各个自由参数具有唯一的估算值。②模型拟合：模型求解，判断各拟合指数是否通过。③模型修正：修正没有拟合的模型，提高模型风险识别自适应性[6]。

3)将修正好的结构模型转换为结构方程，实现基于结构方程的高风险行为自适应监测。

1.1 风险监测结构方程模型构建

将建筑施工过程的预应力作为监测建筑施工高风险行为的评价指标，即监测建筑的预应力。利用高风险行为结构因子j的反馈输入权矩阵，建立建筑结构方程的数学模型。利用模型因子i的密度结构和标准差计算高风险行为的适应度函数。为了使风险监测模型最佳化，进一步完善适应度函数，进行规范化处理，构建基于预应力的结构方程模型[7]，即

(1)

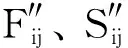
根据式(1)中的参数影响结构方程，对施工行为监测进行处理，迭代次数决定了结构方程的计算量，也影响高风险行为后模型的质量[8]。将预应力高风险行为的误差作为适应度函数J，即

J=1+2(P0lgδ0+P0lgδB)-2(P0lgP0+PBlgPB)，

(2)

式中：B为模型共性因子；PB、P0分别为模型因子的施工风险、密度因子；δ0、δB分别为建筑高风险、模型因子的标准差。

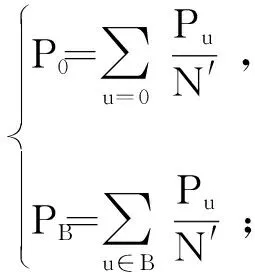
(3)

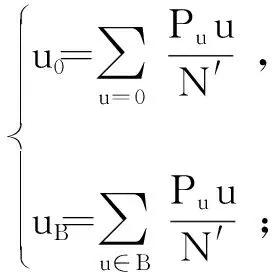
(4)

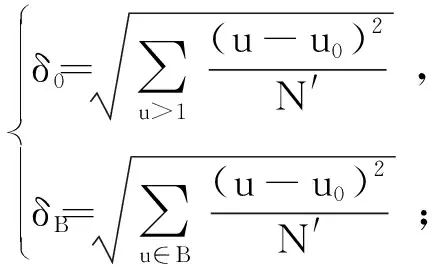
(5)

式中：Pu为风险监测模型的频率因变量；u为像素个数；N′为构建行为监测阈值；u0、uB为高风险行为和模型因子的因变量。

由于预应力高危行为的适应度函数值是不确定的，因此需判断其正负。如果适应度函数是非负数，则需要改变函数公式，即

(6)

式中：K′为修改后的高危行为的适应度函数；C为常数，C>|J|。利用因变量对预应力高风险性数学模型归一化处理，即

(7)

通过计算高风险行为预应力结构因子的权重矩阵和高风险行为的适应度函数，得出建筑的风险预估函数

Y=Wij+J′+K′。

(8)

根据上述得到的风险预估函数，构建初始结构方程模型，即

(9)

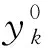
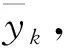
(10)

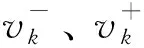
(11)

式中：y0为建筑施工材料寿命预测系数；v-、v+为潜变量区间内的峰值、谷值失效调节系数。图1[9]所示为描述结构方程最简单和最直观的方式。

1.2 结构方程模型校验

结构方程模型构建完成后，为了确保模型中各变量之间的关系，需要对其拟合验证，主要包括3个步骤，即模型识别、模型拟合以及模型修正。

1)模型识别。模型识别的目的是保证被估计参数(风险)能够通过选出的观测数据估计出来[10]。

图1 初始结构方程模型[9]

模型识别采用t规则识别方法，原理为

t≤p(p+g+1)/2，

(12)

式中：t为需要被估计的参数个数；p为内生显变量数；g为外生显变量数。

2)模型拟合。模型拟合的主要工作是参数估计，方法主要有最大似然法、两阶段最小二乘法、广义最小二乘法等[11]。本文中选择第1种模型拟合。最大似然法是用来估计概率模型参数的一种方法，模型拟合结果如表1[12]所示。由表可知，拟合指标的适配度并未都达到规定的标准，因此该模型的拟合优度不达标。由此证明，根据表1选出的指标因素并不能与构建的初始结构模型达成良好的适配，因此需要修正[8]。

表1 结构模型拟合优度评价指标[12]

1.3 结构方程模型修正

模型修正是指通过调整模型，使结构模型进行多模型拟合[13]。图2所示为修正后得到的最终结构模型。

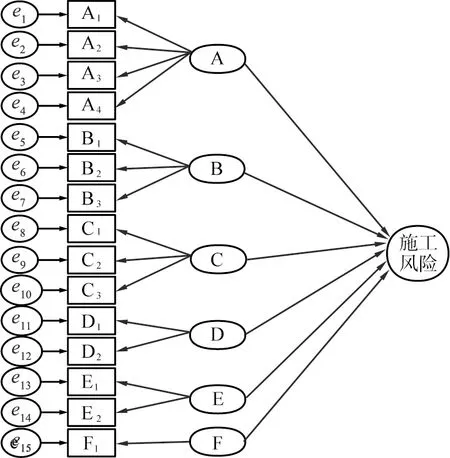
e1—e15—误差项； A1—A4、B1—B3、C1—C3、D1、D2、E1、E2、F1—适配路径，下标1—15为各项风险的排列序号，例如A1为第1个误差项e1的一级适配路径；A、B、C、D、E、F—最终拟合路径。图2 修正后的最终结构模型

再次拟合修正后的结构模型路径图，得到的拟合优度评价指标如表2所示。由表可知，拟合指标的适配度均达到规定的标准，因此该模型的拟合优度达标，结构模型修正结束。

表2 修正后的结构模型拟合优度评价指标

将上述构建好的结构模型转换为结构方程。结构方程是一种分析变量之间关系的工具，实际上是一般线性模型的拓展，其优点是不需要知道所有的解释变量，只需要知道显变量即可，因此比其他模型具有更大弹性[14]。

在结构模型中，主要由2个部分联立组成，即测量模型和结构模型。其中，测量模型包括观测变量和潜在变量2个因素，反映了二者之间的关系，即

x=aA1+b,

(13)

y=cA2+d,

(14)

式中：x为内生指标组成的向量；y为外生指标组成的向量；A1为外生观测变量在外生潜变量上的因子负荷矩阵；A2为内生观测变量在内生潜变量上的因子负荷矩阵；a为外生潜变量；b为外生指标y的误差项；c为内生潜变量；d为内生指标x的误差项。

结构模型仅包括潜变量，反映的是内生潜变量后的和外生潜变量之间同一等级的关系，即

c=Ec+Fa+G，

(15)

式中：E为内生潜变量之间的关系；F为外生潜变量对内生潜变量的影响；G为残差项，反映了在方程中没有被解释的部分。根据式(15)，得到建筑施工高风险行为自适应监测的结构方程。

2 仿真实例测试

为了明确本文中所提风险监测方法的自适应性是否达到要求，设计仿真实例测试。在3dmax软件中模拟建筑施工过程，设置建筑施工存在的高风险行为指标，如表3所示。

表3 建筑施工高风险行为

采用Visual CPP运行库构建结构方程模型，测试所设计结构方程模型对建筑施工高风险行为监测的自适应匹配度，并采用基于支持向量机、基于模糊综合评价2种传统风险监测方法作为实验的对比方法，连接建筑施工临时设施三维数据可视端口，自适应监测某建筑施工项目的高风险行为，得到3种方法的自适应匹配度如图3所示。从图中可以看出，3种方法的自适应监测都没有超出监测门限，说明3种方法都有一定的可行性，本文中所提方法的风险监测数据与监测门限的拟合度为98.75%，基于模糊综合评价方法次之，拟合度为64.83%，基于支持向量机方法与监测门限的拟合度为43.26%。由此可见，相较于2种传统方法，本文中所提方法有较高的自适应匹配度。

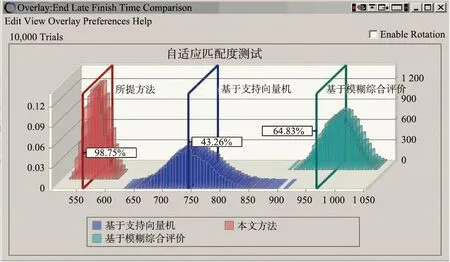
图3 自适应监测匹配度输出结果

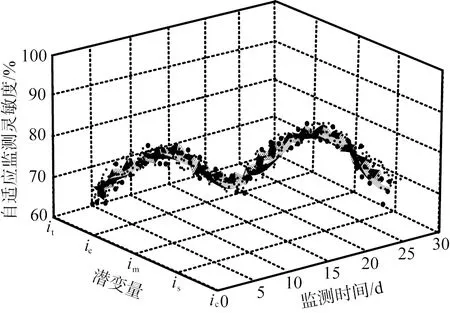
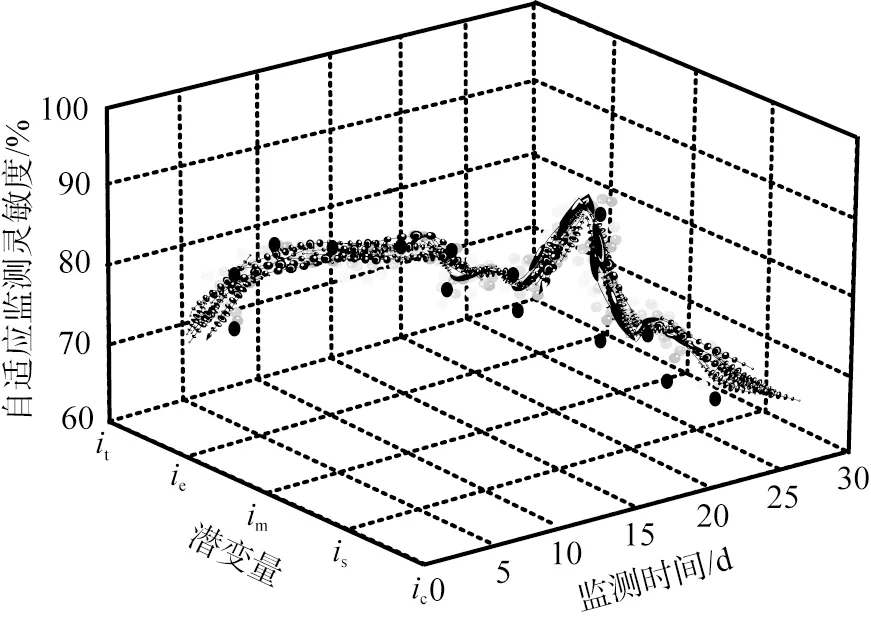
在验证所提方法的自适应匹配度的基础上，测试所提方法的灵敏度。设置施工工期为30 d，测试3种方法对表3中的建筑施工高风险行为指标的监测灵敏度，结果如图4所示。从图中可以看出，所提方法自适应监测灵敏度峰值达到99%，基于支持向量机方法自适应监测灵敏度峰值为78%，基于模糊综合评价方法自适应监测灵敏度峰值为83%，可见本文中所提方法的自适应监测灵敏度最高。

3种方法的自适应监测匹配度输出结果与自适应监测灵敏度输出结果如表4所示。从表中可以看出，利用本文中所提方法进行建筑施工高风险行为自适应监测，监测灵敏度为99%，监测自适应匹配度为98.75%，该结果远好于基于支持向量机、基于模糊综合评价2种传统风险监测方法的结果，由此说明，本文中所提方法性能更好。

3 结论

为了降低建筑施工事故发生的概率，基于结构方程，研究一种新的建筑施工高风险行为自适应监测方法。通过实验得出以下主要结论：

(a)基于支持向量机

(b)基于模糊综合评价

(c)本文中所提方法ic—建筑工程人员的安全素质； is—建筑相关物品的安全状态； im—相关企业的管理水平； ie—周围环境的安全状态； it—建筑施工技术水平。图4 高风险行为自适应监测灵敏度

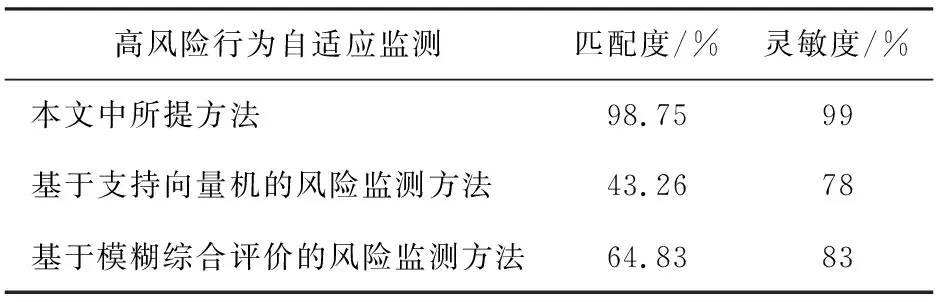
表4 3种方法的自适应监测匹配度输出结果与自适应监测灵敏度输出结果

1)与传统方法相比，该方法的监测灵敏度和匹配度均有极大的改善，说明其自适应性能更好，在一定程度上提高了建筑施工的安全性。

2)由于受到实验平台和实验样本采集环境的限制，性能测试不全面，因此在未来的研究中，需要克服客观环境的限制，争取得出与实际值最为拟合的实验结果。