一种改进全变分配准模型的优化NMG求解方法*

韩晓花，杨奋林

(吉首大学数学与统计学院,湖南 吉首 416000)

图像配准问题是图像处理应用中具有挑战性的任务之一,旨在将不同时间、视角或成像设备的2幅或多幅图像在空间域中实现几何位置的完全对准.图像配准在计算机视觉、模式识别、遥感和医学影像学等领域有广泛应用[1].基于变分偏微分方程(Partial Differential Equation,PDE)的图像配准模型一般会添加一个正则项,以确保得到一个有解的适定问题.选择不同的正则项会导致不同的变形.传统的正则项,如弹性正则项、扩散正则项和曲率正则项,可以产生全局平滑的变形[2],然而这些正则项在某些特定需要的变形中不保留不连续性的位移;全变分(Total Variation,TV)正则项更适合于保留位移场的不连续性[3],但会产生阶梯效应,形成不光滑位移场.为了使所选择的正则项能兼顾位移的全局平滑和保留不连续性,笔者受文献[4-5]的启发,拟选取超曲面函数[6]作为正则项的核函数,建立一个改进TV配准模型,并对非线性多重网格(Nonlinear Multi-Grid,NMG)算法[7-8]进行优化,以期快速有效地求解改进TV配准模型.

1 全变分配准模型的改进

1992年,Rudin等[9]将TV配准模型运用于图像去噪.该模型的正则项能有效地保留不连续性的位移场,从而保留图像边缘信息,但在此过程中会产生阶梯效应,使图像变得模糊.经典的TV正则项可表示为

(1)

(2)

模型(2)的扩散系数

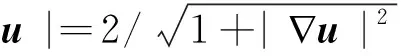
具有以下基本性质:(1)当|∇u|→+∞时,M(|∇u|)→0;(2)当|∇u|→0时，M(|∇u|)→2.这表明,一方面通过减少或停止非均匀区域内的扩散(平滑)过程来保持位移场的不连续性,另一方面在均匀区域内各向同性平滑位移场.即在非均匀区域采用类似TV的正则化,在均匀区域采用类似扩散或二次的正则化.

模型(2)对应的欧拉-拉格朗日方程为

(3)

其中力项fl(u)是拟合项的一阶导数且是非凸的,

fl(u)=(T(u)-R)∂ulT(u),

可用一阶泰勒展开转化为凸问题进行求解.

2 非线性多重网格算法的优化

2.1 基于层析技术的NMG法

NMG算法是求解大型非线性方程组的有效方法之一.其基本思想是:利用非线性前光滑方法(一种迭代松弛技术)，求出一个近似解计算残量和误差,使光滑的误差项在一个较粗的网格上很好地限制和逼近;进入V-循环,在最粗网格上求解关于误差的非线性残量方程;采用粗网格修正,将误差插值回细网格,用于细网格逼近的校正;使用非线性后光滑,以消除插值误差中引入的一些新的高频成分.

为了在计算过程中避免产生额外误差,配准精度更高,笔者在限制过程中采用层析技术,将粗网格上的误差插值回细网格.

优化NMG算法的具体求解过程如下:方程(3)化为

N[u[v]]u[v+1]=G[v].

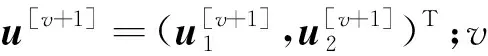
(4)

(5)

这里σll为力项fl(u)关于ul的一阶偏导数，

2.2 数值离散化

给定n×n像素的离散图像,图像域Ω=[0,n]2(本研究中n的值均为2的幂次方),网格尺寸Δx=Δy=1.网格点(i,j)的位置

(xi,yj)=((i-0.5)Δx,(j-0.5)Δy),i,j∈[1,n].

网格点(i,j)处u的值记为ui,j.用有限差分格式离散方程(3),得到网格点(i,j)处的离散方程

fl(u)i,j=(gl)i,j.

(6)

其中:

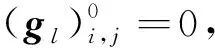
接下来,介绍用于网格间距为(Δx,Δy)的矩形网格Ωh与网格间距为(2Δx,2Δy)的矩形网格Ω2h之间的网格传输函数.

2.3 平滑方法

本研究中使用的平滑方法是基于典型滞后扩散不动点方法作的改进[10],即在不动点框架中引入内外耦合迭代方法,该迭代方法在正则化项和数据拟合项中都是半隐式的.输入图像R和T、正则化参数α、松弛因子ω、内部迭代次数k、最大迭代次数K、容差q,利用当前近似计算所有(i,j)的Di,j,在每一步对非线性方程组进行全局线性化.然后,采用逐次超松弛(Successive Over Relaxation, SOR)迭代作为内迭代,求解每个外步骤v的相关线性系统,使所有差分方程同时更新.定义在网格点(i,j)的SOR迭代方法的第k步为

算法1平滑方法:uh←SMTV(uh,gh,R,T,K,α,ω,q).

Step 2 分别利用(4),(5)式计算N[u[v]]和G[v].

Step 3 令w←u,采用for循环,执行SOR内部迭代求解,

算法2优化NMG算法:uh←ENMG(uh,gh,R,T,k,α,l,N).

Step 2 计算残量,rh=Gh-Nhvh.

Step 4 进入V-循环,在最粗网格上求解关于近似解v2h的残量方程Nhu2h-Nhv2h=r2h.

Step 5 计算误差,e2h=u2h-v2h.

Step 7 执行后光滑(算法1),uh←SMTV(uh,gh,R,T,k,α,ω).

3 数值实验

利用Matlab软件进行仿真实验.选取像素大小为128×128的手部图片作为测试的单模图像,配准前相似性测度为200.554 6.参考图像、模板图像及它们的差图像如图1所示.

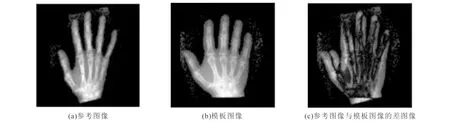
图1 手部测试图像Fig. 1 Hand Test Image

分别用NMG算法和优化NMG算法求解改进TV配准模型,图2和图3用来比较算法的有效性.用优化NMG算法分别求解TV配准模型和改进TV配准模型,图3和图4用来比较模型的优劣性.

图2 NMG-改进TV配准图像Fig. 2 NMG-Improved TV Registration Image

图3 优化NMG-改进TV配准图像Fig. 3 Optimized NMG-Improved TV Registration Image

图4 优化NMG-TV配准图像Fig. 4 Optimized NMG-TV Registration Image

由图2(a)和图3(a)可见,相比NMG算法,优化NMG算法对模板图像(图1(b))的整体配准效果更好,基本接近参考图像(图1(a));由图2(b)和图3(b)可见,用NMG算法在手腕部位的网格折叠比较严重,而用优化NMG算法的网格变化均匀.

由图3(a)和图4(a)可见,相比TV配准模型,改进TV配准模型对模板图像(图1(b))手指和手腕部位的配准效果更好,更接近参考图像;由图3(b)和图4(b)可见,TV配准模型配准图像的位移场在手指部位的网格折叠比较严重,而改进TV配准模型配准图像的位移场的网格更光滑.

当各算法的参数都调为最优(松弛因子ω=1.1)且达到相同的外部迭代步数时,相似性测度与内部迭代次数的变化趋势如图5所示.

图5 相似性测度-内部迭代次数曲线Fig. 5 Variation Trend Between Similarity Measure and Internal Iteration Number

由图5(a)和(c)可见,分别用NMG算法和优化NMG算法求解改进TV配准模型,优化NMG算法的配准时效性高于NMG算法;由图5(b)和(c)可见,用优化NMG算法分别求解TV配准模型和改进TV配准模型,改进TV配准模型的配准时效性明显高于TV配准模型.

相似性测度、误差、内部迭代次数和迭代时间见表1.

表1 相似性测度、误差、内部迭代次数和迭代时间

从表1可知：优化NMG-改进TV配准手部测试图的相似性测度、误差和内部迭代次数比NMG-改进TV的分别减少3.505 8,1.748 1%,6,优化NMG-改进TV的迭代时间约为NMG-改进TV的20%;优化NMG-改进TV配准手部测试图的相似性测度、误差和内部迭代次数比优化NMG-TV的分别减少18.751 9,9.350 1%,19,优化NMG-改进TV的迭代时间约为NMG-TV的19%.

4 结语

笔者通过引入超曲面函数，建立了改进TV配准模型,该模型在全局平滑位移场的同时还能保留不连续性的位移.为了快速有效地求解改进TV配准模型,对NMG算法作了优化.仿真实验结果表明：分别用NMG算法和优化NMG算法求解改进TV配准模型,优化NMG算法能更快速地收敛并取得稳定的数值解,且求解耗时更短,误差更小;用优化NMG算法分别求解TV配准模型和改进TV配准模型,改进TV配准模型的配准图像的精度更高,整体配准效果更令好.未来考虑将交替方向乘子法与NMG算法相结合,设计出更快速有效的数值方法,进一步提高配准时效和配准质量.