基于COTS的宇航计算单元冗余架构可靠性研究

雷华舟，钟 杰，吕升林

(1.中国科学院 空间光电精密测量技术重点实验室，成都 610209; 2.中国科学院 光电技术研究所，成都 610209; 3.中国科学院大学 计算机科学与技术学院，北京 100049; 4.中国人民解放军 空军装备部驻成都地区第五军事代表室，成都 610209)

0 引言

近年来，由于商业需求在航天领域的不断发展，商业载荷需求呈现爆发式增加。传统的以科技载荷为需求的3～5年的载荷研制周期不能满足商业航天的业务需求，而且航天级器件一般因为供货周期长，价格昂贵而且性能往往落后于地面上的同级别器件的原因，所以采用高性能商业级现货器件代替传统航天级器件作为商业航天公司在成本控制领域发展的一个方向。在宇航应用中，计算单元能否长时间地稳定、可靠工作对于目标任务的实现具有关键作用，由于高性能商业级器件不是为了宇航应用而生产，所以为了提升其在宇航应用中的可靠性，利用适当的容错策略和冗余设计，使其达到所需的设计目标。[1]随着计算技术的发展，在冗余设计上有传统采用静态的热备、冷备的方式[2-3]，也有较新的基于动态重构的方式[4-5]，不同的设计和策略因为应用场景不同各有特点。因此各种冗余设计的可靠性是一个值得研究的重要问题。

目前针对冗余设计可靠性主要研究指向单一项目前对宇航电子设备进行设计前的预估，判断宇航电子设备是否能够满足系统的可靠性设计，为系统方案提供必要的技术支撑[6-7]。另外，从理论角度采用新的理论进行新的可靠性模型搭建和软硬件容错策略设计也是学者们研究的另一方向[8-9]。为了更低成本的商业化应用，部分学者尝试将方向引向商业设计上计算单元架构可靠性相互间比较研究[10]。

综上所述，以往的研究主要集中为单一项目提供技术支撑和新可靠模型的搭建，对于架构可靠性比较研究较少。本文在冗余设计可靠性理论基础上，用马尔可夫链模型数值分析计算方法，考虑计算单元的仲裁切换模块，针对商业航天任务周期时长的背景，对几种冗余设计架构可靠性进行仿真、比较分析，为商业航天载荷的设计提供参考。

1 计算单元容错设计结构

常见的基于COTS器件宇航计算单元一般采用“计算核心+FPGA”的异构组合，近年来也出现了基于大容量FPGA构成的可重构计算单元[4，11-12]。对于常见的异构组合需要考虑其仲裁切换模块的可靠性，而对于基于FPGA构成的计算单元还需要考虑由其系统的最大特点是可以通过重新配置，进行系统的重构，通过可重构机制使得系统得以修复。

由于具有可修复能力的电子设备进行可靠性分析时过程相对比较复杂。本文以动态重构三模冗余作为可修复设备的代表进行可靠性分析。主要针对比较常用的双机冷备、双机热备、三模冗余以及两热一冷这几种冗余结构计算单元的可靠性进行分析。

1.1 双机冷备结构

双机冷备份结构设计原理如图1所示，正常状态下采用的主节点上电，备节点不上电。双机冷备份结构在仲裁切换模块正常，没有发生故障时，主节点正常工作进行运算处理，计算单元内的备节点不会发生故障；当主节点发生故障时，激活备节点，对主节点进行替换；当备节点也发生故障时，系统失效。当仲裁切换节点发生故障时，主节点正常工作，备节点不会发生故障；当主节点故障时，由于仲裁切换模块发生故障无法切换，系统失效。

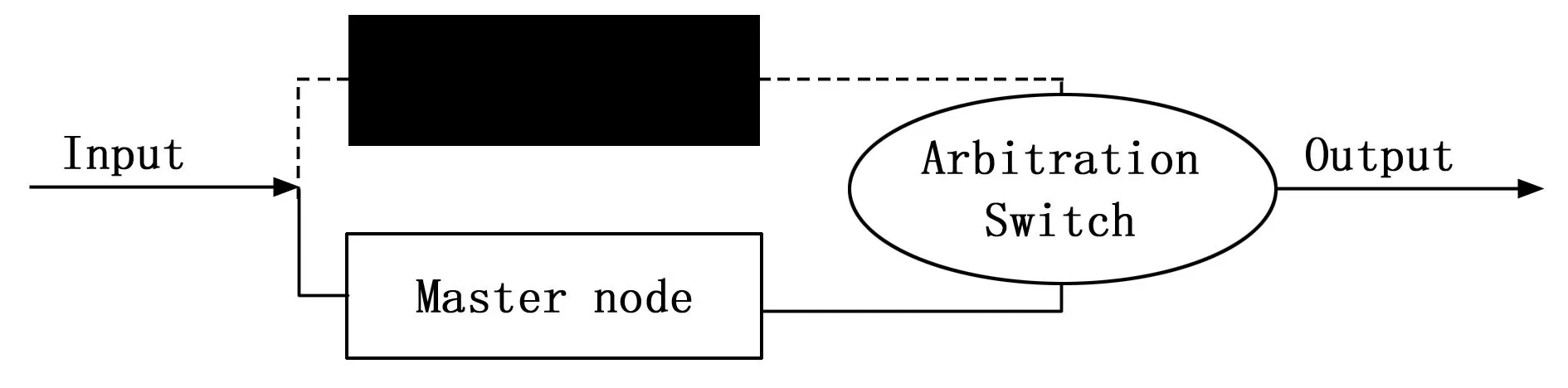
图1 双机冷备份重组结构拓扑图

1.2 双机热备结构

双机热备份重构设计原理如图2所示，采用的双机热备份，热备份与冷备份不同在于正常情况下，计算单元内的备节点也有可能发生故障。双机热备份在仲裁切换模块正常，主节点正常工作时，计算单元工作正常；当备节点也发生故障时，系统失效。当仲裁切换节点发生故障时，主节点正常工作，备节点发生故障，系统正常工作；当主节点故障时，由于仲裁切换模块发生故障无法切换，系统失效。

图2 双机热备份重组结构拓扑图

1.3 三模表决冗余结构

常规三模表决设计原理如图3所示，采用的三模表决，正常状态下3个节点均正常工作对输入信号进行运算，仲裁切换模块表决，系统正常输出；当其中1个节点发生故障，另2个节点正常工作时，仲裁切换节点将会屏蔽故障节点的影响；当出现2个节点及以上节点发生故障时，系统失效。当仲裁切换节点出现故障时，由于无法进行仲裁或者仲裁出错，系统失效。

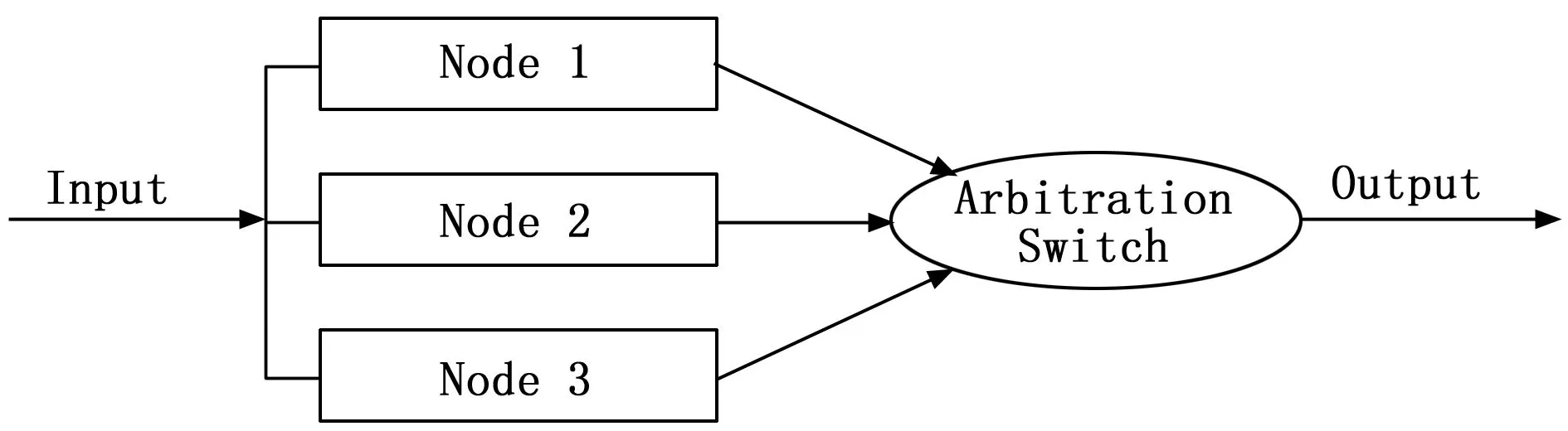
图3 三模表决冗余结构拓扑图

1.4 三模冗余重组结构

三模冗余重组结构设计一般应用在大容量可重构FPGA上，其结构如图4所示，采用的三模表决的仲裁策略，正常状态下3个节点均正常工作，系统正常输出；当其中1个节点发生故障，另2个节点正常工作时，仲裁切换节点屏蔽故障节点的影响，系统通过内嵌的故障诊断、识别，然后进行故障清理等手段让故障节点恢复正常，在不影响计算单元工作的情况下，将其接入系统，恢复到三模表决的工作状态；当出现2个节点及以上节点发生故障时，系统失效。当仲裁切换节点出现故障时，由于无法进行仲裁或者仲裁出错，系统失效。

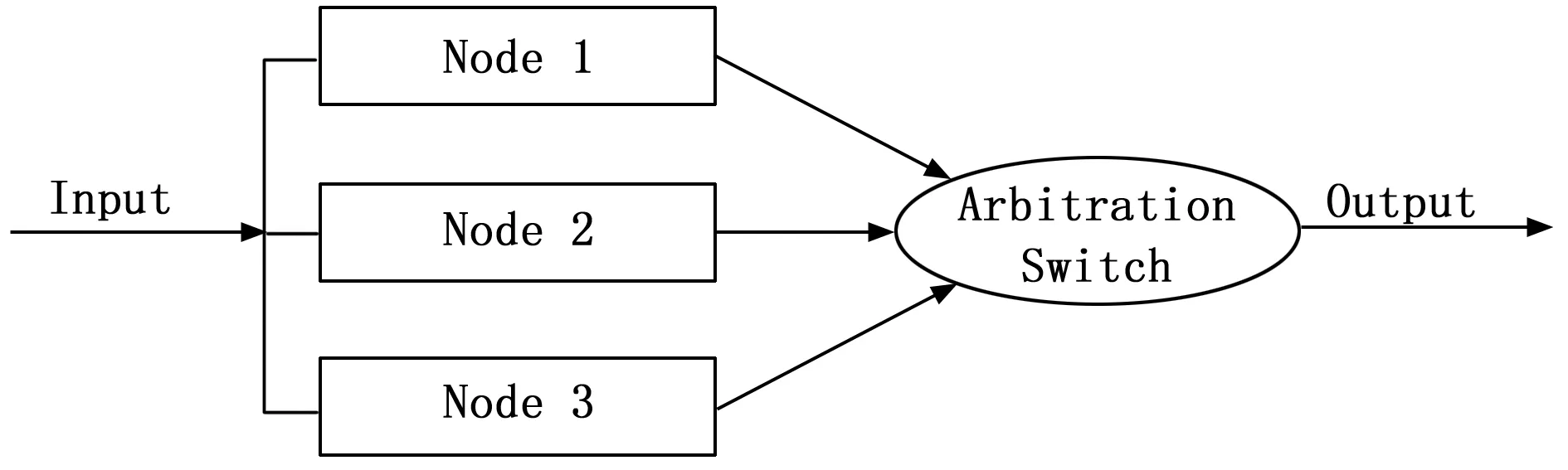
图4 三模冗余重组结构拓扑图

1.5 两热一冷冗余结构

两热一冷冗余结构设计原理如图5所示，采用1个双节点热备加一个节点冷备的节点架构，正常状态下两个热节点均正常工作，系统正常输出；当其中1个热节点发生故障，仲裁切换节点激活冷节点，与正常节点重新构成双节点热备。

考虑仲裁切换节点出现故障的时间，其工作状态分为：首先仲裁切换节点出现故障，当其中1个热节点发生故障，系统只能以单节点状态工作；其中1个热节点首先发生故障，之后仲裁切换节点出现故障，系统以双节点热备状态工作。

图5 两热一冷冗余结构拓扑图

2 系统设计结构工作状态

由于计算单元的容错设计结构不一致，其在工作时遭受故障时的工作状态会产生变化以保证系统的正常运行，针对计算单元不同的工作状态，采用马尔科夫随机过程对其可靠性进行建模，考虑到不同单元失效率λC、λAW和维修率μC，对不同结构计算单元的可靠性指标进行评价。

2.1 双机冷备结构工作状态

由图1所示的双机冷备结构，正常状态S11，没有故障节点，主节点当班；当主节点发生故障，由状态S11变为状态S12，备节点被激活，作为当班节点；当仲裁切换节点发生故障，由状态S11变为状态S13，主节点仍作为当班节点工作。当主节点、仲裁切换节点发生故障，由状态S12变为状态S14，备节点被激活，作为当班节点；当主节点、备节点发生故障，由状态S12变为状态S16，系统失效。当仲裁切换节点、主节点发生故障，由状态S13变为状态S15，系统失效。当所有节点故障，变为状态S17，系统失效。其工作状态如表1所示。

表1 双机冷备份重组结构工作状态表

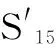
图6 双机冷备结构系统状态转移图

2.2 双机热备结构工作状态

由图2所示的双机热备结构，正常状态S21，没有故障节点，主节点当班；当主节点或者备节点发生故障，由状态S21变为状态S22，另一节点被激活，作为当班节点；当仲裁切换节点发生故障，由状态S21变为状态S23，主节点仍作为当班节点工作。当主节点、仲裁切换节点或者备节点、仲裁切换节点发生故障，由状态S22变为状态S24，另一节点被激活，作为当班节点。当仲裁切换节点、备节点发生故障，由状态S23变为状态S24，主节点仍作为当班节点工作；当仲裁切换节点、主节点发生故障，由状态S23变为状态S25，系统失效。当主节点、备节点发生故障，由状态S22变为状态S26，无当班节点，系统失效；当所有节点故障，变为状态S27，系统失效。其工作状态如表2所示。

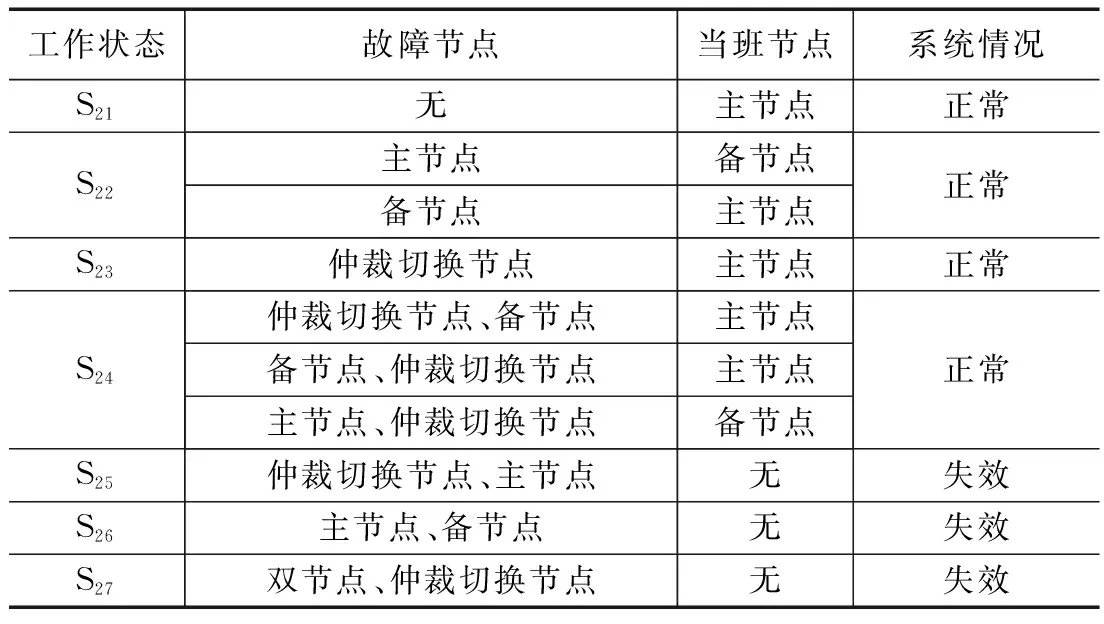
表2 双机热备份重组结构工作状态表

图7 双机冷备结构系统状态转移图

2.3 三模表决冗余结构工作状态

由图3所示的三模表决冗余结构，正常状态S31，没有故障节点，仲裁节点3/3仲裁。当某计算节点发生故障，由状态S31变为状态S32，仲裁节点2/3仲裁；当仲裁切换节点发生故障，由状态S31变为状态S35，系统失效。当某计算节点再次发生故障，由状态S32变为状态S33，仲裁节点1/3仲裁，系统失效；当某计算节点，仲裁切换节点发生故障，由状态S32变为状态S36，系统失效。当仲裁切换节点、某计算节点发生故障，由状态S35变为状态S36，系统失效。当所有计算节点发生故障，由状态S33变为状态S34，系统失效；当某两计算节点、仲裁切换节点发生故障，由状态S33变为状态S37，系统失效。当仲裁切换节点、某两计算节点发生故障，由状态S36变为状态S37，系统失效。当所有节点发生故障，变为状态S38，系统失效。其工作状态如表3所示。

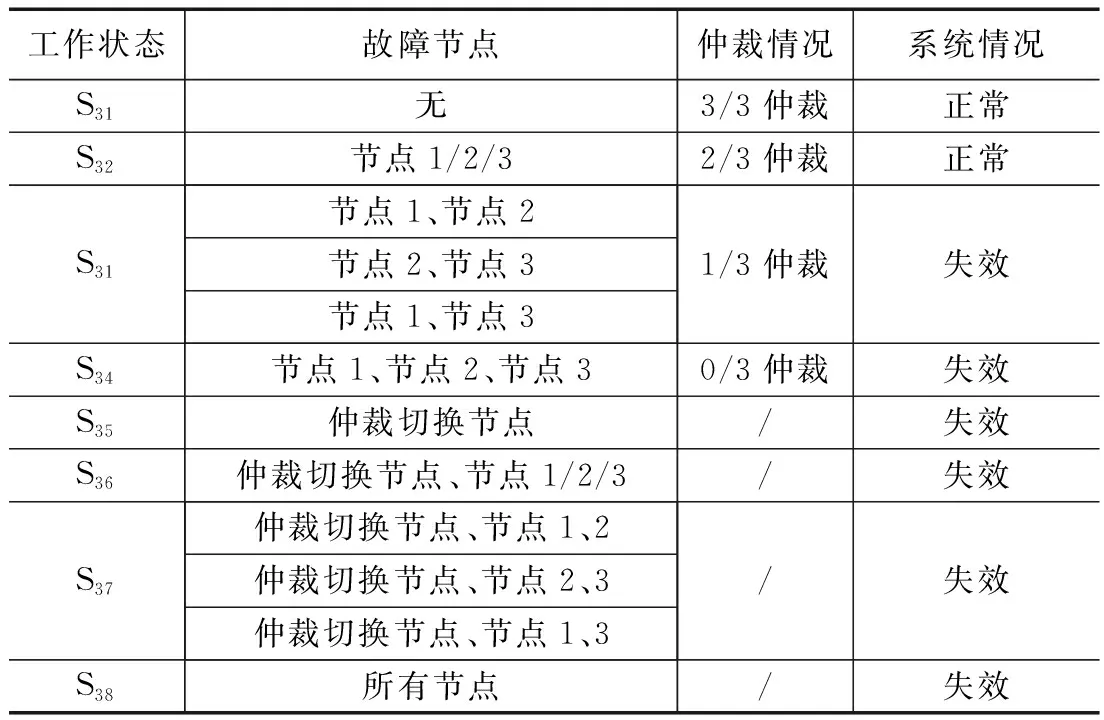
表3 三模表决冗余结构工作状态表

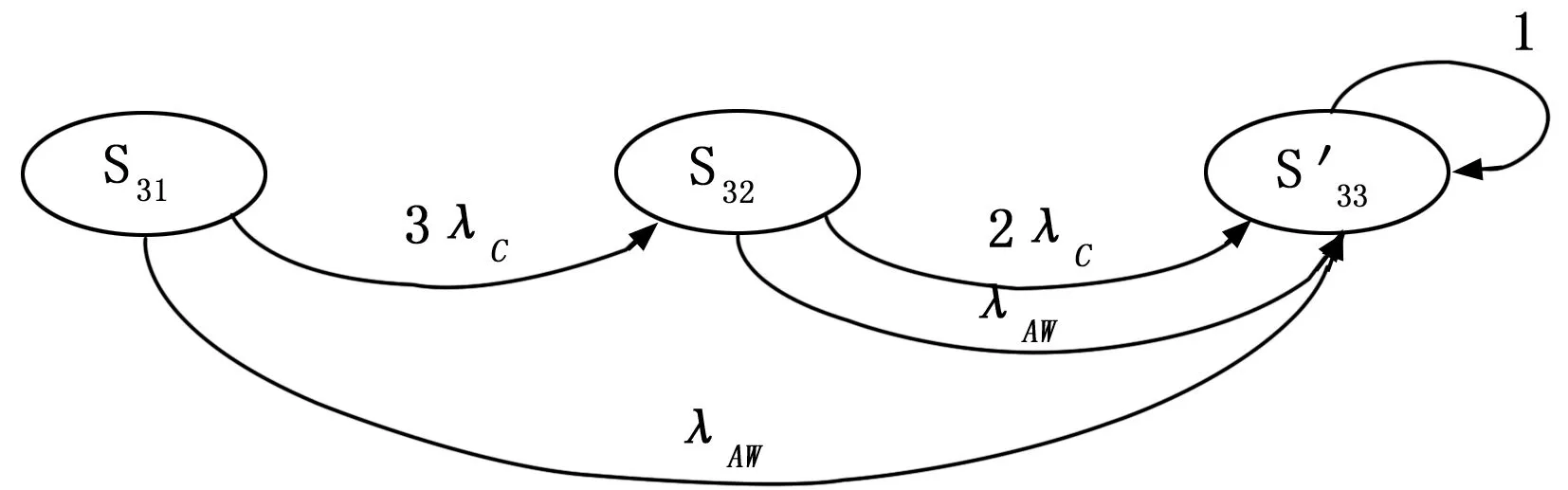
图8 三模表决冗余结构系统状态转移图

2.4 三模冗余重组结构工作状态

由图4所示的三模表决冗余结构，工作模式与三模表决冗余结构基本一致，主要区别在于当某一计算单元出现故障之后，将以某一修复率对该计算单元进行修复，其工作状态如表4所示。

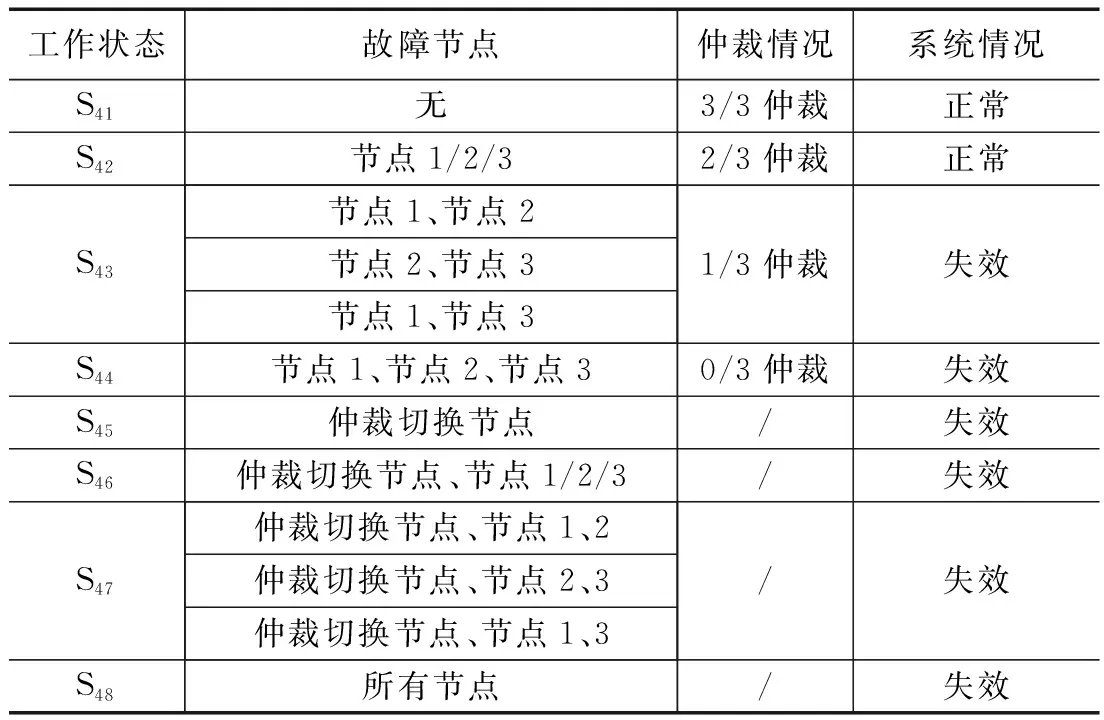
表4 三模冗余重组结构工作状态表

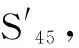
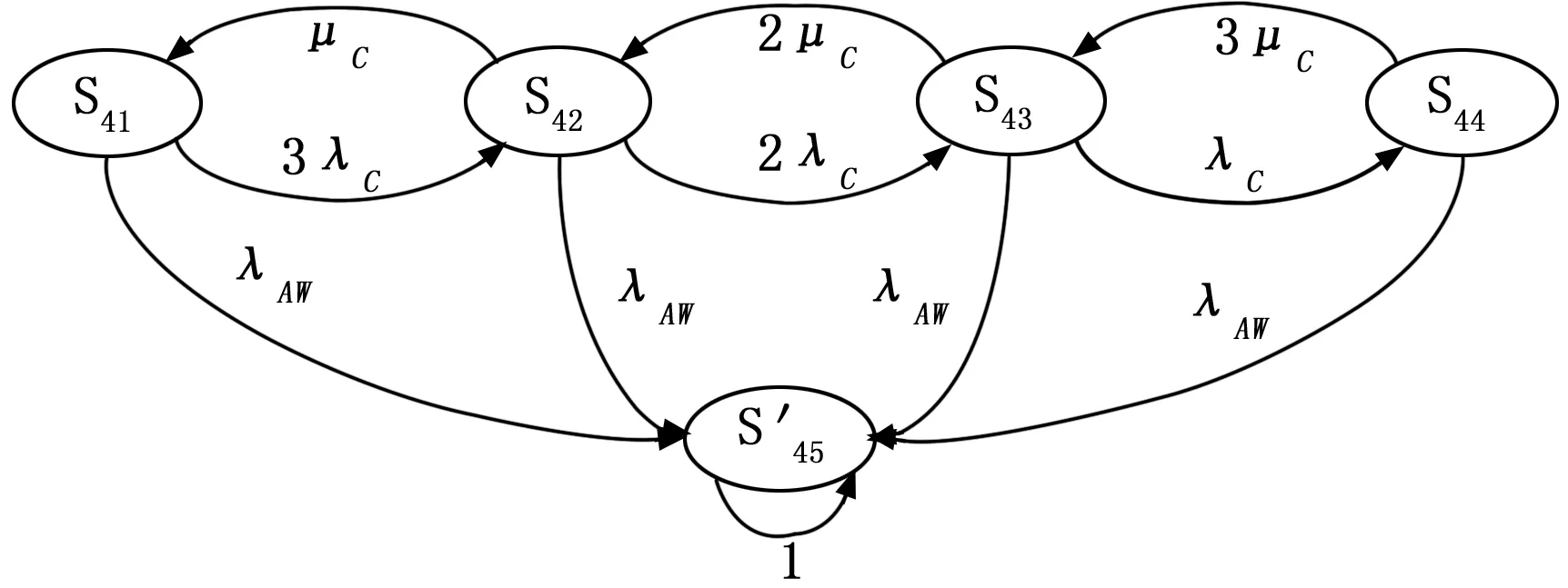
图9 三模冗余重组结构系统状态转移图

2.5 两热一冷冗余结构工作状态

由图5所示的两热一冷冗余结构，正常状态S51，没有故障节点，由主节点与备节点1构成双机热备结构，主节点当班。当主节点或者备节点1发生故障，启动备节点2，组成新的双机热备结构，由状态S51变为状态S52。当任意两个计算节点发生故障，转化为单机系统，由状态S52变为状态S53；当一个计算节点和仲裁切换节点先后发生故障，由状态S52变为状态S54。当仲裁切换节点和备节点1先后发生故障，主节点仍做当班机，系统正常，由状态S51变为状态S55；当仲裁切换节点和主节点先后发生故障，仲裁切换失效，系统失效，由状态S51变为状态S56。当仲裁切换节点、主节点、备节点1先后发生故障，系统失效，由状态S55、S56变为状态S59。当任意两计算节点故障后，仲裁切换节点失效，系统由状态S53变为状态S57、S58；当所有的3个计算节点故障后，系统由状态S53变为状态S5a。当某计算节点和仲裁切换节点故障后，降为双机系统，此时如非当班节点发生故障，则系统工作正常，系统由状态S54变为状态S58；此时如当班节点发生故障，则系统工作失效，系统由状态S54变为状态S5b。当所有节点发生故障，变为状态S5c，系统失效。其工作状态如表5所示。

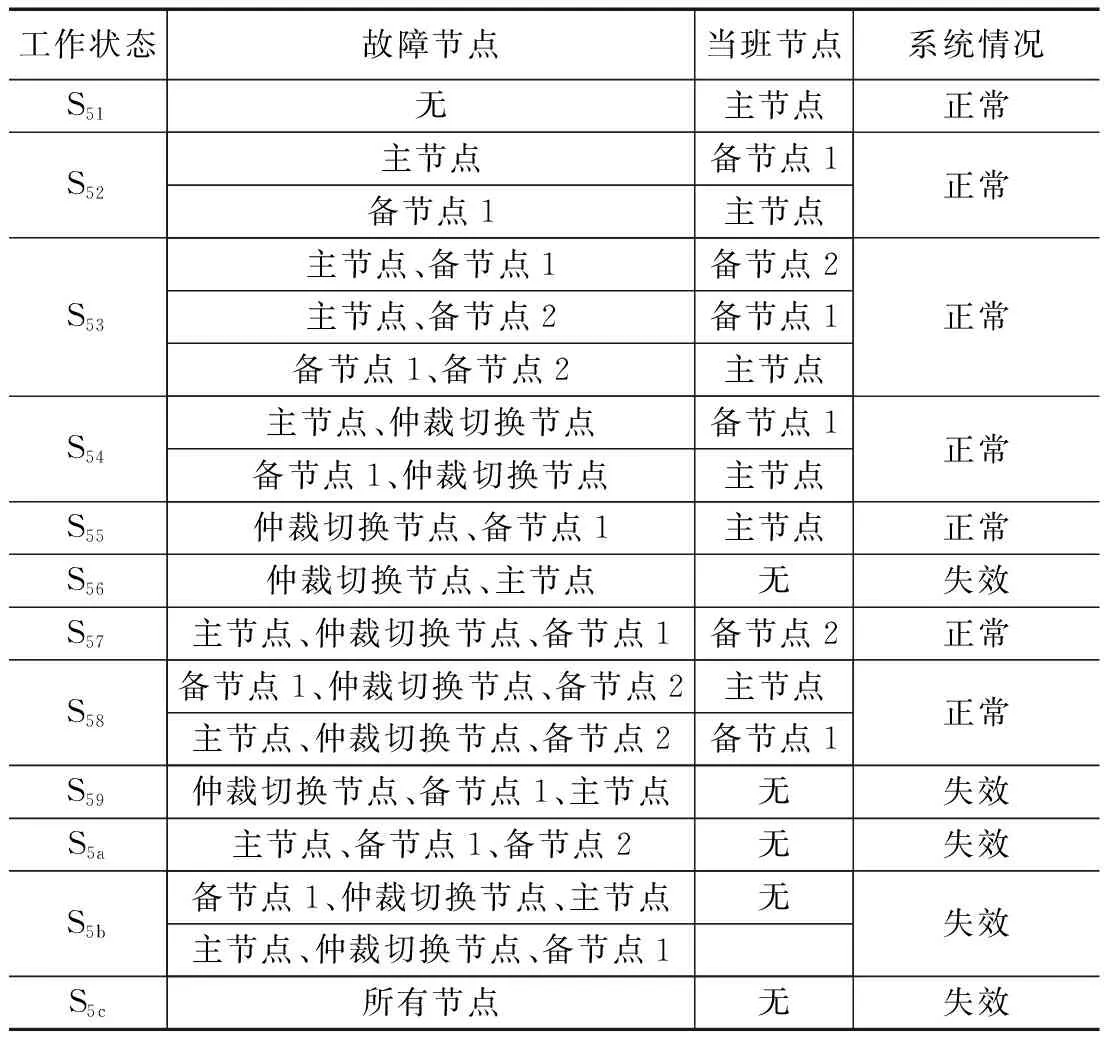
表5 两热一冷冗余结构工作状态表

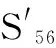
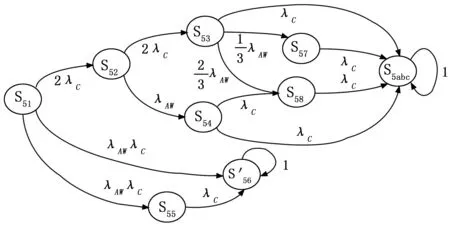
图10 两热一冷冗余结构系统状态转移图

3 可靠性模型分析及计算

在研究系统的可靠性之前，首先对系统做如下假设：

1)假设系统中除了处理器模块和表决切换单元外，其他系统的可靠度均为1；

2)每个计算核心模块的失效率为λC，维修率为μC，表决切换单元的失效率为λAW，同时假设失效分布和维修时间分布为指数分布；

3)某一时刻只有一个模块发生故障；

4)系统开始工作时，各单元都为无故障状态，系统整体处于完好状态。

基于以上假设，对各结构的可靠性进行研究。

3.1 双机冷备结构

根据图6，其马尔克夫状态可做以下的数学描述：时刻t+Δt结构状态的条件概率与t时刻结构状态由全概率公式得到，考虑当Δt→0时，得到如下状态微分方程组：

(1)

考虑系统的约束条件：

初始条件：

将上述方程组进行Laplace变换解出后，进行反Laplace变换可得双机冷备重组结构可信度：

R1(t)=PS11(t)+PS12(t)+PS13(t)+PS14(t)

(2)

3.2 双机热备结构

根据图7双机热备结构的状态转移图，其马尔克夫状态可做以下的数学描述：时刻t+Δt结构状态的条件概率与t时刻结构状态由全概率公式得到，考虑Δt→0当时，得到如下状态微分方程组：

(3)

考虑系统的约束条件：

初始条件：

将上述方程组进行Laplace变换解出后，进行反Laplace变换可得双机热备重组结构可信度：

R2(t)=PS21(t)+PS22(t)+PS23(t)+PS24(t)

(4)

3.3 三模表决冗余结构

根据图8，其马尔克夫状态可做以下的数学描述：时刻t+Δt结构状态的条件概率与时刻t结构状态由全概率公式得到，考虑当Δt→0时，得到如下状态微分方程组：

(5)

考虑系统的约束条件：

初始条件：

将上述方程组进行Laplace变换解出后，进行反Laplace变换可得三模表决冗余结构可信度：

R3(t)=PS31(t)+PS32(t)

(6)

3.4 三模冗余重组结构

根据图9，考虑三模重组一般采用大容量FPGA构成的，其马尔克夫状态可做以下的数学描述：有λC=λAW，时刻t+Δt结构状态的条件概率与t时刻结构状态由全概率公式得到，考虑当Δt→0时，得到如下状态微分方程组：

(7)

考虑系统的约束条件：

初始条件：

将上述方程组进行Laplace变换解出后，进行反Laplace变换可得三模表决冗余结构可信度：

R4(t)=PS41(t)+PS42(t)

(8)

3.5 两热一冷冗余结构

根据图10三模冗余重组结构的状态转移图，其马尔克夫状态可做以下的数学描述：时刻t+Δt结构状态的条件概率与t时刻结构状态由全概率公式得到，考虑当Δt→0时，得到如下状态微分方程组：

(9)

考虑系统的约束条件：

初始条件：

PS51(0)=1,PS52(0)=PS53(0)=PS54(0)=PS55(0)=PS57(0)=PS58(0)=0

将上述方程组进行Laplace变换解出后，进行反Laplace变换可得三模表决冗余结构可信度：

R5(t)=PS51(t)+PS52(t)+PS53(t)+PS54(t)+PS55(t)+

PS57(t)+PS58(t)

(10)

4 可靠度仿真及对比分析

宇航计算单元对可靠性的要求非常苛刻，在预计寿命内的可靠度不低于0.99[13]。经过特别的处理和加固的宇航级或军品级的电子元器件，其失效率λ一般在10-9～10-8/h之间，目前的商用VLSI技术所能达到的失效率为10-7/h，但一般的商业级或工业级的电子元器件，其失效率λ在10-6～10-5/h之间[14]。

根据式(2)、(4)、(6)、(8)、(10)可以分析与比较失效率和修复率对不同形式系统可靠性的影响，对这5类结构组成的计算单元正常工作5年(4.38×104h)的可靠度进行比较。选取计算核心失效率λC=10-6/h，仲裁切换单元失效率λAW=10-6/h，恢复率μC=100λAW=10-4/h(恢复率主要对于三模冗余重组结构，其由大容量FPGA构成，故λAW=λC，下文同理)，所得曲线如图11所示。

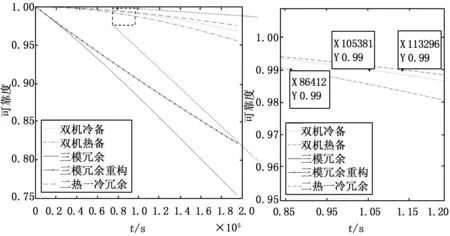
图11 λC=10-6/h，λAW=10-6/h，μC=100 λAW=10-4/h各架构可靠度变化曲线

取计算核心失效率λC=10-5/h，仲裁切换单元失效率λAW=10-5/h，恢复率μC=100λAW=10-3/h，所得曲线如图12所示。

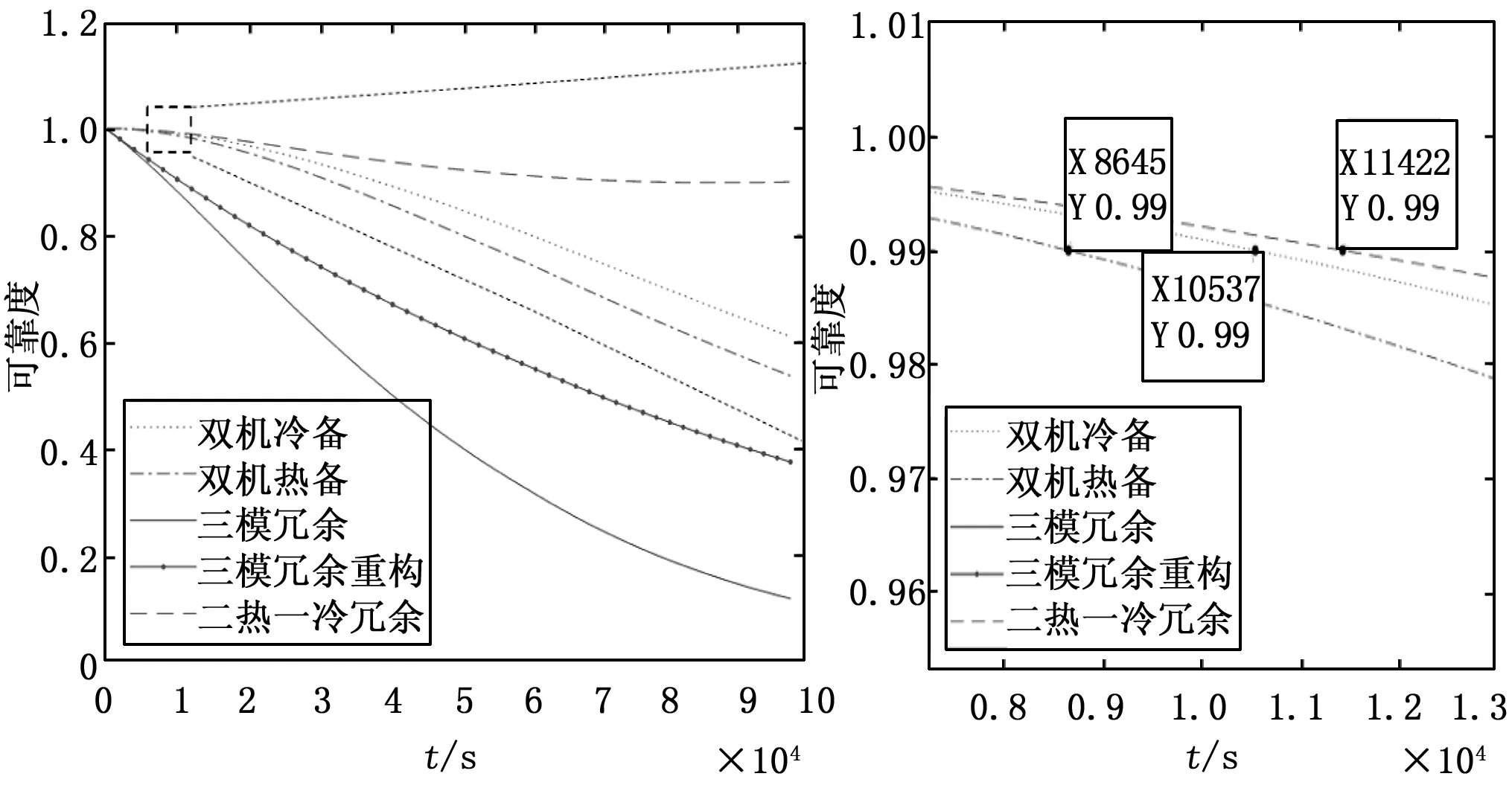
图12 λC=10-5/h，λAW=10-5/h，μC=100λAW=10-3/h各架构可靠度变化曲线

可以明显由图12看出，λC=10-5/h，λAW=10-5/h，失效率较大时，无论采取什么结构，系统保持可靠度不低于0.99的预期寿命不足1.2×104h，其中能保持可靠度不低于0.99最长结构为两热一冷，时间为1.14×104h，最远低于一般载荷正常工作5年(4.38×104h)的预期寿命；而当选取的λC=10-6/h，λAW=10-6/h，失效率较小时，双机热备、双机冷备和两热一冷结构能够保持可靠度不低于0.99的预期寿命超过一般载荷正常工作5年(4.38×104h)的预期寿命，分别达到8.6×104h、10.5×104h和11.3×104h。由图12、图13可明显看出三模冗余重组结构由于修复率的关系，相同工作时间内明显比一般三模冗余结构系统可靠性更高，但无论是常规的三模冗余还是三模冗余重组结构的计算单元其可靠度都极低，远不能达到一般载荷正常工作的预期寿命。

分别选取计算核心失效率λC=10-6/h、λC=10-5/h，仲裁切换单元失效率λAW在10-7～10-5/h下，分析和比较不同架构可靠性，所得曲线如图13、图14所示。

(a)λAW=10-5 h-1 (b)λAW=10-6h-1 (c)λAW=10-7h-1图13 λC=10-6/h，不同λAW下各架构可靠度变化曲线(t=2×105 h)

(a)λAW=10-5h-1 (b)λAW=10-6 h-1 (c)λAW=10-7 h-1图14 λC=10-5/h，不同λAW下各架构可靠度变化曲线(t=105 h)

在λC=10-6/h情况下，双机冷备冗余结构可靠度不低于0.99的运行时间由4.6×104h先后提升至10.5×104h、14.1×104h；双机热备冗余结构可靠度不低于0.99的运行时间由4.4×104h先后提升至8.6×104h、10.2×104h；三模冗余结构可靠度不低于0.99的运行时间由0.1×104h先后提升至0.9×104h、4.4×104h；两热一冷冗余结构可靠度不低于0.99的运行时间由3.4×104h先后提升至11.1×104h、51.1×104h。

在λC=10-5/h情况下，双机冷备冗余结构可靠度不低于0.99的运行时间由1.0×104h先后提升至1.4×104h、1.4×104h；双机热备冗余结构可靠度不低于0.99的运行时间由0.8×104h先后提升至1.0×104h、1.0×104h；三模冗余结构可靠度不低于0.99的运行时间由0.1×104h先后提升至0.4×104h、0.5×104h；两热一冷冗余结构可靠度不低于0.99的运行时间由1.1×104h先后提升至5.5×104h、51.5×104h。

如表6所示，相同λAW下，λC的可靠度是决定系统可靠度的绝对因素，λC的提高能大幅提高系统的可靠性。在λC不变情况下，不同冗余结构可靠度都随着λAW提高能有效提升系统整体的可靠性，λAW在到达某一个值之后对系统可靠性的影响就会逐渐减弱。

5 结束语

本文对5种典型宇航计算单元冗余架构建立了马尔可夫模型，根据可靠性理论对各架构的可靠性进行了计算、分析和比较。三模表决架构虽具有实时性强、发生一次故障系统工作不间断等优点，但从分析结果看，无论是常规三模表决架构还是动态重构的三模表决架构都不适合长时间任务。另一方面，在考虑制造成本、预期寿命、实时性和系统复杂度的不同影响的情况下，可以采取不同的冗余架构或者在计算核心和仲裁单元采用不同失效率的器件。具有双机冷备的冗余架构在制造成本占有一定优势，既能够满足较长预期寿命相对而言可靠性也能够达到要求；具有两热一冷的冗余架构在制造成本优势较小，既能够满足长时间的预期寿命和相对而言较高的可靠性要求，但结构相对复杂；具有双机热备的冗余架构在制造成本上占有一定优势，既能够满足一般的预期寿命相对而言可靠性也能够达到要求，并且在实时性上会表现较好。

表6 不同结构不同失效率可靠度不低于0.99运行时间(104 h)