基于微分预报的机载雷达稳定平台自抗扰控制系统设计

晁令锦,梅 栋,俞竹青

(常州大学 机械工程学院，江苏 常州 213164)

0 引言

合成孔径雷达是一种可以在极低能见度条件下得到类似光学照片的高分辨率成像雷达。由于其几乎不受气候条件限制，实现全天候对地观测的特点[1]。越来越多地被安装于有人或无人机上进行军事侦查，军用引导打击，以及灾情勘测等军用与民用领域。但是由于在载机飞行过程中易受到气流扰动而导致雷达跟随飞机受到扰动引起合成孔径雷达成像模糊，无法完成既定任务。因此作为可以保障雷达成像稳定、清晰，隔离飞机扰动的机载雷达稳定平台越来越多的受到各国重视。

机载雷达稳定平台是一种集机械结构和伺服控制于一体的精密复杂设备[2]。其根据载机陀螺仪检测到的扰动角速度，驱动伺服电机采用反向补偿原理进行扰动补偿以保证机载雷达指向稳定[3]，成像清晰。目前在商业中普遍采用PID控制作为机载雷达稳定平台扰动抑制的控制方案，虽然PID控制便于设计，计算简单，但其本质仍然是一种线性控制方案[4]。随着对机载雷达稳定平台控制精度需求的提高，PID对于机载雷达稳定平台这样的非线性，强耦合以及存在不确定参数的对象并不能达到很好的扰动抑制效果。对此很多研究人员采用现代控制理论如模糊控制，自适应控制，神经网络控制等[5]，或与PID控制结合的方法以提高对稳定平台的扰动抑制能力。例如，文献[6]采用模糊PID串级控制，通过模糊理论在线调节PID所需参数有效提高了稳定平台的扰动抑制能力。文献[7]采用神经网络自适应控制算法提高稳定平台的扰动的抑制能力。以上方式虽有效提高了对稳定平台这种非线性对象抑制扰动的能力，但由于这些算法设计复杂，计算量大，对数学模型精度要求高等等问题并不容易在实际工程中应用[8]。

近十几年来，自抗扰控制由于其设计方便，计算简单，不依赖于数学模型的精度等优点受到广泛关注[9]。自抗扰控制由韩京清教授在文献[10]提出，其核心是通过扩张状态观测器将系统的未建模状态与扰动合并为“总合扰动”实时观测并将结果反馈给非线性状态反馈其进行动态补偿以达到消除扰动的目的。自提出以来，许多研究人员将其应用到各种非线性控制系统中，并取得了令人满意的效果。例如，文献[11]采用自抗扰控制以提高航空稳定平台的扰动隔离度，文献[12]采用串联扩张观测器的方法提高雷达稳定平台对扰动的抑制能力，文献[13]将自抗扰控制应用于改善电梯门电机转速控制性能，并取得了良好的控制效果等等。但通过实验发现，随着控制系统阶数的增加，自抗扰控制对扰动观测的实时性变差，导致对扰动抑制能力有所下降[14]。

综合上述问题，本文提出一种基于预报修正的机载雷达稳定平台自抗扰控制方案。在保持原算法结构不变的条件下，根据微分跟踪器的特性将扩张状态观测器的扰动观测输出通过“先微分，后预报”之后，在进行扰动补偿。通过仿真实验证明，采用先微分后预报的自抗扰控制方案有效提高的对扰动观测的实时性，并与PID控制和原自抗扰控制对比，证明其对扰动的抑制能力。

1 平台数学模型简化与扰动分析

1.1 数学模型简化

机载雷达稳定平台是由驱动电机，传动机构，平台外框架，以及传感器部件组成。当受到扰动时，传感器将检测的信号反馈给控制装置，控制电机驱动传动机构从而带动与外框架直接相连的雷达天线反向转动以消除扰动，其传动结构如图1所示。

图1 平台传动结构图

本文以某型号两轴两框架机载雷达稳定平台为分析对象，其以直流无刷伺服电机为驱动元件，根据电机动力学原理可得电机运动学方程为

(1)

其中：Tl为负载转矩，J为电机轴转动惯量，ω为传动系统角速度，t为时间，Tm为电机产生的转矩可由以下公式计算：

Tm=CtI

(2)

Ct为电机电磁系数，I为电机电枢电流。

电机角度可由电机角速度积分求出，公式如下：

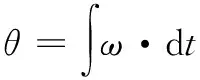
(3)

考虑初始状态为0的情况下，将式(1)～(3)采用拉氏变换为：

(4)

令负载转矩Tl=0，可得其电流与角度开环传递函数为：

(5)

令x1=ω,x2=θ，取控制量为：u=I，角度θ为输出量。根据状态空间方程表达式可得雷达稳定平台状态空间方程表达式为：

(6)

1.2 扰动分析

机载雷达稳定平台在运行过程中主要受到的扰动来源有传动机构的摩擦力矩扰动与载机角速度扰动，其中载机角速度扰动时雷达稳定平台最主要的克服对象，其扰动简图如图2所示。

图2 平台扰动分析简图

随着机载雷达稳定平台应用范围的增加，对其扰动抑制能力也提出了更高的需求，尤其是在复杂空况下面对不稳定气流的连续扰动时的抗干扰能力。

2 “先微分，后预报”的自抗扰控制器

2.1 自抗扰控制简介

自抗扰控制是由韩京清教授提出的一种基于“主动抗扰”思想的非线性控制理论，其主要有微分跟踪器，扩张状态观测器和非线性状态反馈三部分组成。其原理是将扩张状态观测器的估计量与非分跟踪器的输出量之差通过非线性反馈器(一种类似于非线性的PID控制器)产生控制量，并将系统的未知扰动以及未建模状态统称为“总和扰动”通过扩张状态观测器实时观测并在系统中进行动态补偿，以达到消除扰动的目的。其原理如图3所示。

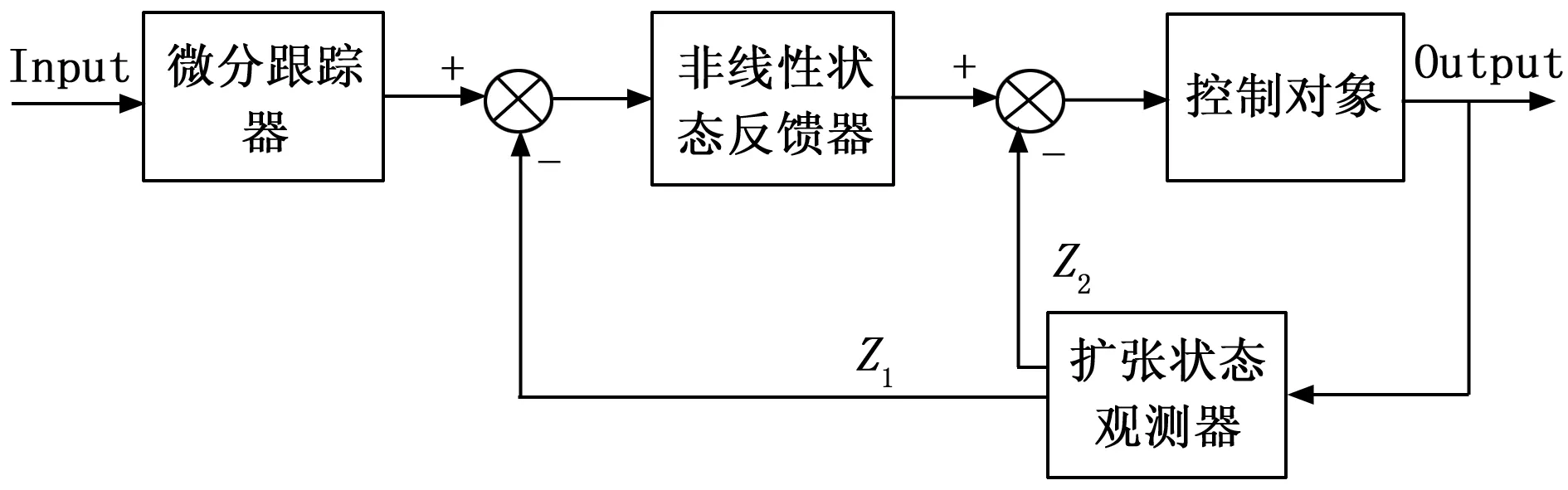
图3 一阶自抗扰控制器原理图

图3中，Z1为估计的状态量，Z2为估计的总和扰动。

2.2 平台扩张观测器设计

扩张状态观测器作为自抗扰控制的核心，主要是将系统的总和扰动进行实时估计与动态补偿。根据公式(6)平台的状态空间方程可得平台系统的状态方程为：

(7)

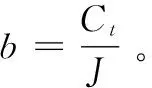
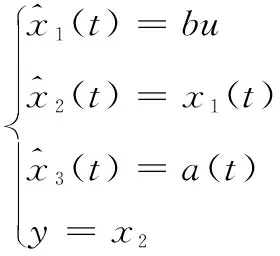
(8)

(9)

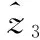
(10)

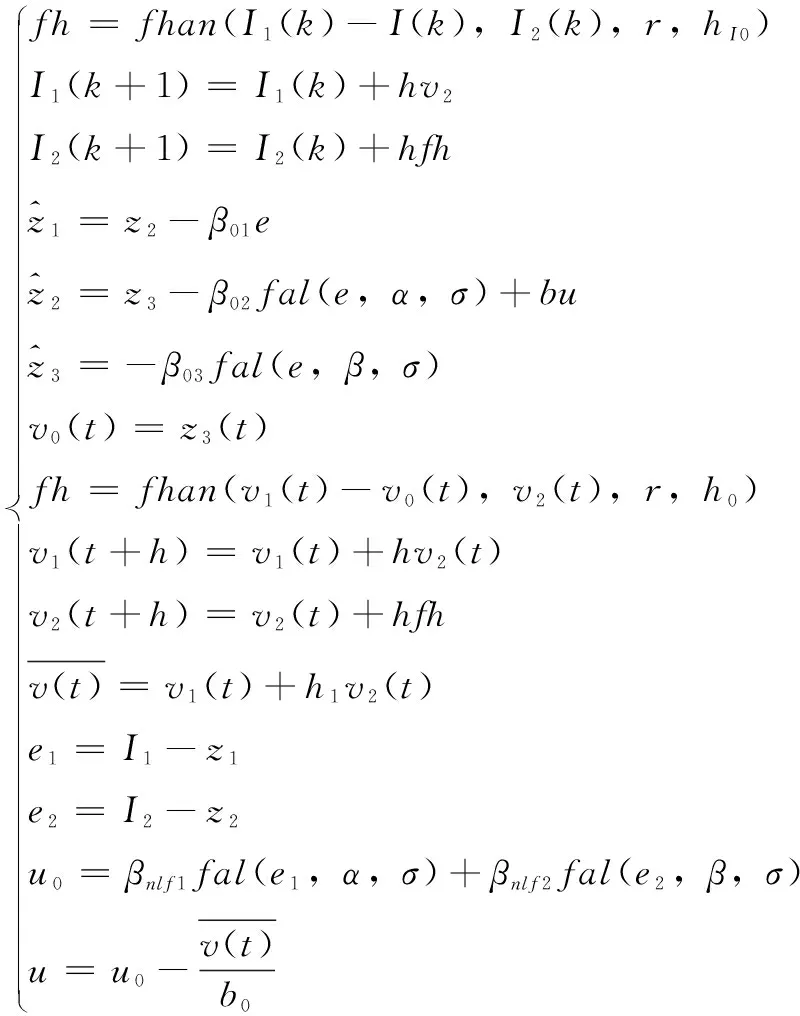
(11)

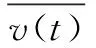
3 仿真实验与分析

3.1 基本实验参数确立

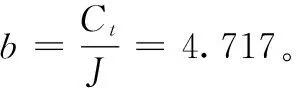
(12)

3.2 扰动观测实验

在平台实际工作过程中实际受到的最大扰动频率为2 Hz，因此本文以低频扰动段与中频扰动段的扰动作为观测对象进行考察。对控制系统分别加入频率为0.5 Hz和 1 Hz的正弦扰动，观察基于微分预报的自抗扰控制器对扰动观测的实时效果。其结果如图4和图5所示。

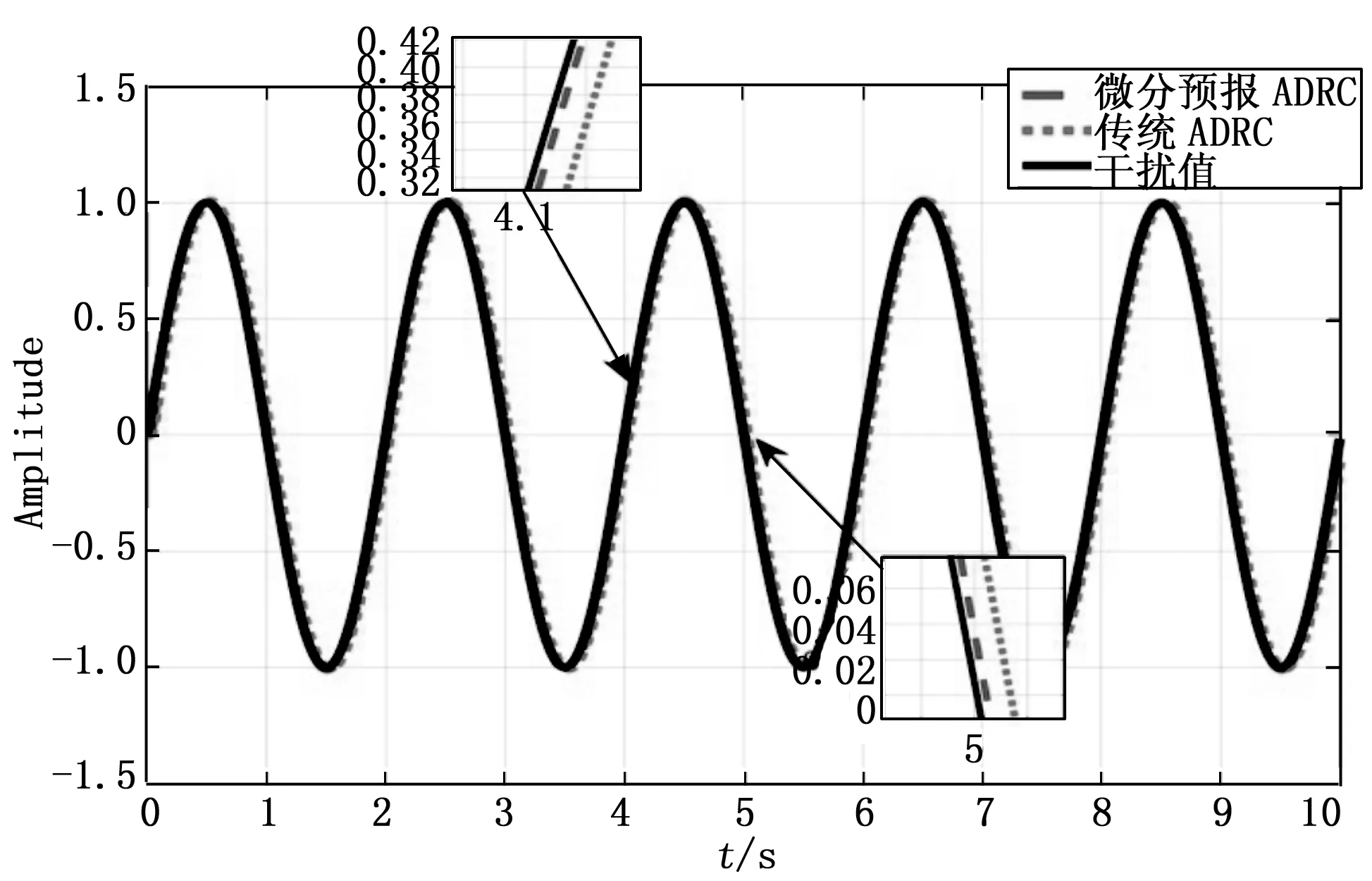
图4 0.5 Hz正弦扰动观测结果

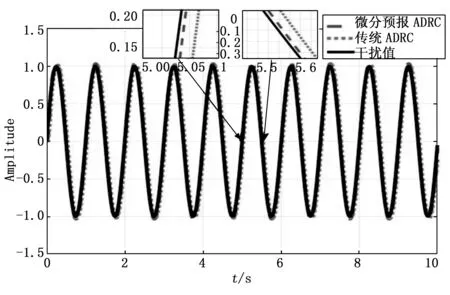
图5 1 Hz正弦扰动观测结果

如图4以及图5所示，微分预报ADRC代表基于先微分后预报的自抗扰控制器，传统ADRC代表经典的自抗扰控制器，干扰值代表所施加的正弦扰动。由图4可以看出，传统的自抗扰控制器对扰动的观测的滞后性明显，实时性效果难以令人满意，而基于先微分后预报的自抗扰控制器虽然相比于原干扰值仍存在一定的滞后性，但比较与传统自抗扰控制器其实时观测能力大幅提高，有效地改善了控制器的扰动观测滞后的状况。

3.3 阶跃响应分析

阶跃响应是分析一个控制系统基本特性的重要方法，本文通过与PID控制对比，验证先微分后预报自抗扰控制的优点，其结果如图6所示，具体数据见表1。

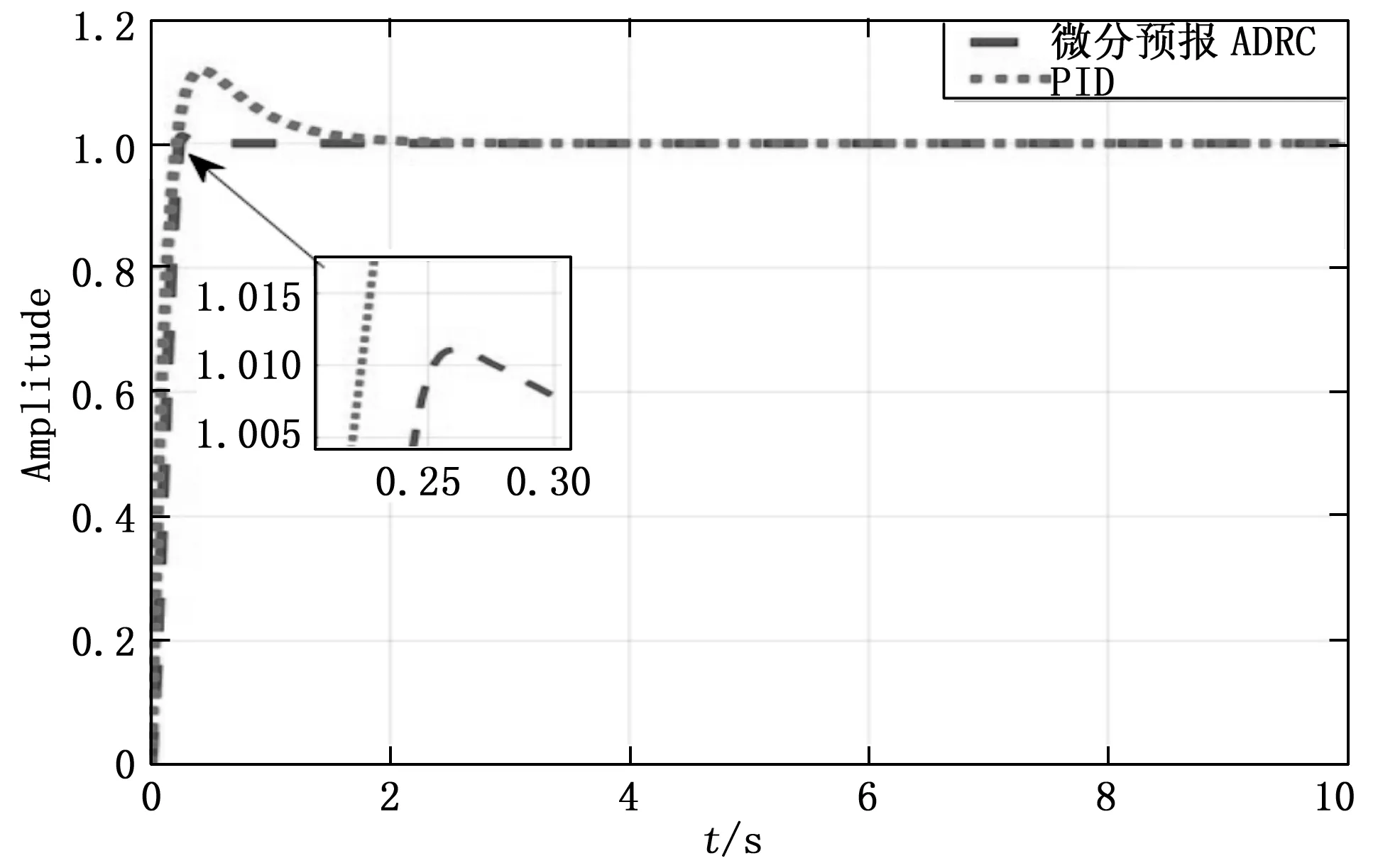
图6 阶跃响应对比图

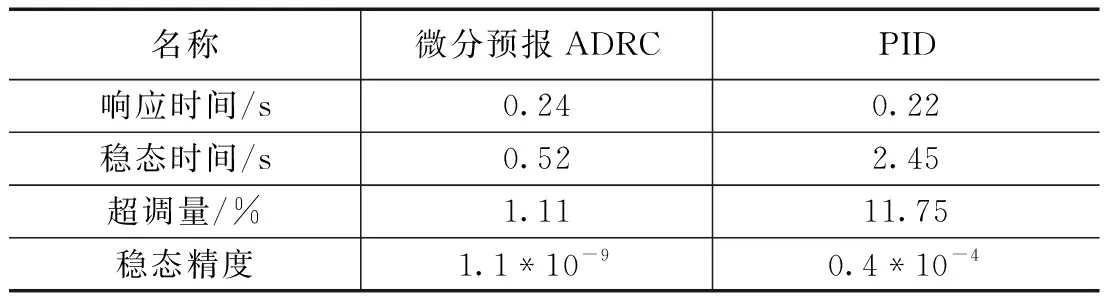
表1 阶跃响应数据表

由图6和表1可以看到，PID控制的响应时间略快于先微分后预报的自抗扰控制器，但先微分后预报的自抗扰控制器稳态时间只有0.52 s，是PID控制的21.2%。对系统响应的超调量PID控制达到11.75%，而先微分后预报的自抗扰控制器仅有1.11%，不足其十分之一。对于系统响应后的稳态精度，先微分后预报的自抗扰控制器更是远远小于PID控制器。

3.4 扰动抑制试验

当系统达到稳态对其加入幅值为1时间为0.1 s的方波扰动，观察两个控制器对扰动的抑制能力。结果如图7所示，具体数据列于表2。

图7 单次扰动结果

表2 单次扰动数据表

如图7所示，在系统达到稳态后，在5 s时刻对其加入方波扰动。由表2可知，当系统受到幅值为1的方波扰动时，先微分后预报的自抗扰控制器的响应幅值仅有0.005，是PID控制的12.8%。当受到扰动后PID控制再次达到稳定所需要的时间为2.05 s，而先微分后预报自抗扰控制器仅需0.47 s，远小于PID控制。对于经过扰动后两个控制器的稳态精度都有所下降，但先微分后预报的自抗扰控制器仍远远优于PID控制几个数量级。

随着机载雷达应用范围的扩展，机载雷达经常需要在恶劣空况下执行任务，此时对雷达稳定平台对连续扰动的抑制能力就有很大考验。因此本文最后对系统加入幅值为1周期为2 s的连续方波扰动观察两个控制器在连续扰动情况下的工作情况。结果如图8所示。

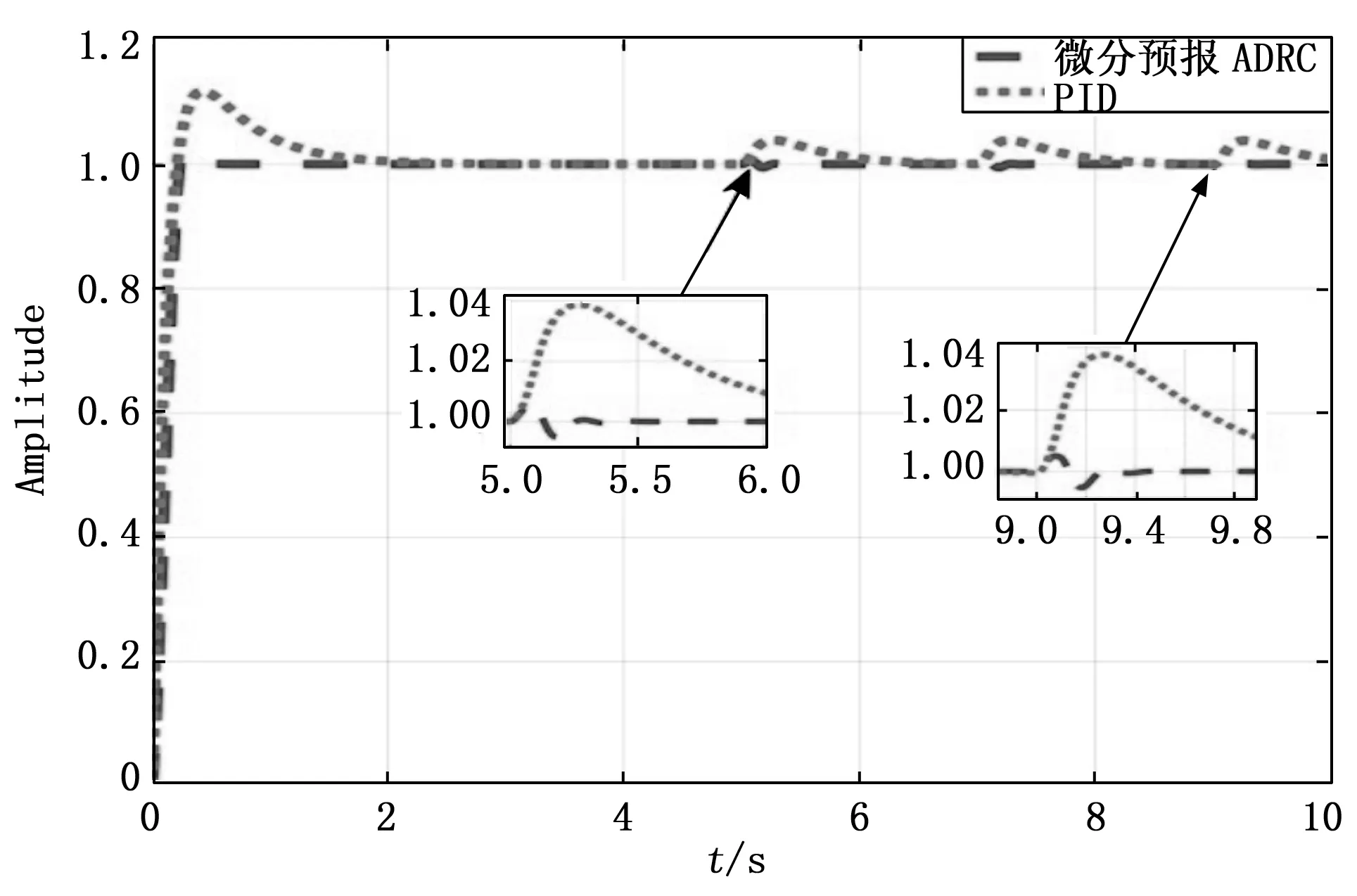
图8 连续扰动比较图

由图8可以看出，当受到连续的方波扰动时，传统的PID控制已不能很好地完成既定任务，而基于先微分后预报的自抗扰控制每次受到很小的扰动后马上回归稳定。由以上可以看出基于先微分后预报的自抗扰控制器拥有更优秀的抑制扰动能力。

4 结束语

为了进一步提高机载雷达稳定平台的抗干扰能力，尤其是在复杂空况下抑制连续扰动的能力以满足对其越来越高的精度需求，本文提出一种基于“先微分，后预报”的机载雷达稳定平台自抗扰控制方案。根据微分跟踪器的特性，将扩张观测器的扰动观测输出先通过微分跟踪器的微分预报之后在送入系统以消除扰动。通过以上实验证明，基于先微分后预报的自抗扰控制器大大改善了传统自抗扰控制器对扰动观测的滞后现象，有效提高其对扰动观测的实时性。通过阶跃响应实验和扰动实验证明，与传统的PID控制相比，基于先微分后预报的自抗扰控制策略不仅超调量小、稳态精度高，而且对扰动的抑制能力更为优秀，尤其对连续扰动情况下的表现更为优秀。由此可以看出，本文提出的基于先微分后预报的自抗扰控制策略更加适用于需要在复杂空况下工作的机载雷达稳定平台，以保证其工作精度需求。