一个具有恐惧效应的捕食者-食饵系统的无穷远平衡点

赵 一 锦

(四川大学 数学学院，四川 成都 610064)

0 引言

种群动力学模型是描述种群与环境、种群与种群之间相互竞争、相互作用的动力学关系的数学模型，可用于描述、预测、调节和控制物种的发展过程与发展趋势[1].两个不同物种的种群在同一个生态环境中生存，它们之间的关系包括捕食者与被捕食者、寄生物与寄主、相互竞争以及互惠共存[2].早在20世纪20年代，Volterra[3]已经利用微分方程解释了第一次世界大战期间捕食者鱼类数量增加的事实.随着种群动力学的发展，科研工作者们建立了一系列微分方程模型来刻画捕食者种群与食饵种群之间的关系.实验发现，动物可以对感知到的捕食风险表现出反捕食者反应[4]，除此以外，恐惧可能影响食饵幼年时期的生理状况并进一步对它们在成年后的生存构成不利[5].Zanette等[6]通过实验证明即使没有直接捕杀的影响，感知到的捕食风险也会影响食饵种群的繁殖.

2016年，Wang等[7]引入了一个恐惧效应f(k,y)，它满足

用于解释由于恐惧导致的反捕食者的防御成本，其中，y表示捕食者的种群数量，k反映了驱使食饵做出反捕食行为的恐惧程度.他们由此进一步提出了一个具有恐惧效应且带有Holling-II型功能反应的捕食者-食饵模型

(1)

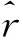
和一个内部平衡点E2:(1,y*)，其中y*是由简化系统

的系数表示的，其中

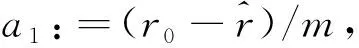
它们是由系统(1)作变换

(2)

得到的.在双曲型情形下，Wang等[7]通过讨论系统在平衡点处Jacobi矩阵的行列式和迹的符号给出了平衡点的稳定性.利用Dulac-Bendixson定理和Poincaré-Bendixson定理，讨论了闭轨的存在性问题.在中心型情况(特征值为一对共轭纯虚根)下，通过计算和讨论第一阶焦点量的符号，给出了Hopf分岔产生一个极限环的参数条件，并通过数值模拟发现可以通过Hopf分岔产生两个极限环.笔者发现文献[7]中并没有讨论轨道在无穷远处的性态.

(3)

其中

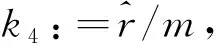
首先利用Poincaré变换证明该系统有两个无穷远平衡点且均为退化平衡点(两个零特征值)，其中之一在其两个特殊方向的任意角邻域中都存在极坐标半径随时间变化率为零的点，因此无法构造正常区域以满足无转的条件.通过构造广义正常区域给出无穷远平衡点附近轨道的走势，最后再利用Briot-Bouquet变换进一步确定有几条轨线连接此无穷远平衡点.结果表明，当两物种种群数量较大时，种群数量都不稳定，并且食饵因感受到捕食风险而产生恐惧，进而表现出的反捕食反应对种群生态系统没有影响.

1 无穷远平衡点分析

为探讨捕食者和食饵的种群数量很大时，两种群的相互作用和发展趋势，下面将分析系统(1)无穷远处轨道的走向.

定理1系统(1)在第一象限内仅有Ix:(+,0)和Iy:(0,+)两个无穷远平衡点，且均为退化平衡点.沿着x轴，y轴和第一象限内的任意方向，系统(1)都有唯一一条轨线离开Ix.沿着x轴(y轴)，系统(1)有唯一一条轨线进入(离开)Iy.此外，在第一象限内没有轨线连接Iy.

证明先用Poincaré变换x=1/z和y=u/z将系统(3)化为

其中dτ=dt/z3.因为只考虑系统(3)的第一象限，故上述时间尺度变换并不改变轨道的走向.求解方程组U(u,0)=0，Z(u,0)=0.不难看出，uz平面的原点O1:(0,0)是系统(4)在u轴上的唯一平衡点，从而系统(3)在x轴上有无穷远平衡点Ix.由于系统(4)在O1的Jacobi矩阵为全零矩阵，有两个零特征值，故O1是退化的.根据文献[8]中第二章里的定理3.1，只需讨论特殊方向上的轨道走向.当r→0时，通过极坐标变换u=rcosθ和z=rsinθ，系统(4)可写为

其中，G(θ)≡0，H(θ)=k1(cosθ+sinθ).再利用Briot-Bouquet变换[8-10]

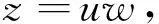
将O1打散并将系统(4)简化为

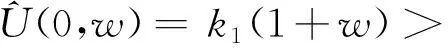
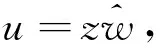
将O1打散并将系统(4)简化为

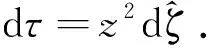
再用另一个Poincaré变换x=v/z和y=1/z将系统(3)化为

(5)

其中，

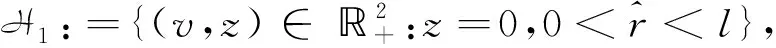
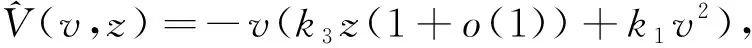
当k5>1时，令

在L1上，因为

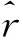
将O2打散并将系统(5)简化为

(6)

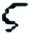
2 结论

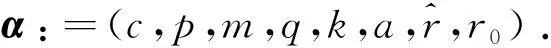
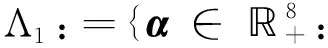
当E2稳定时(α∈Λ2)，文献[7]中模拟出系统(1)可能存在两个极限环.当E2不稳定时(α∈Λ3)，系统(1)至少存在一个极限环，这与文献[7]中的结论一致.当两物种种群数量较大时，种群数量都不稳定并且食饵因感受到捕食风险而产生恐惧，进而表现出的反捕食反应对种群生态系统没有影响.

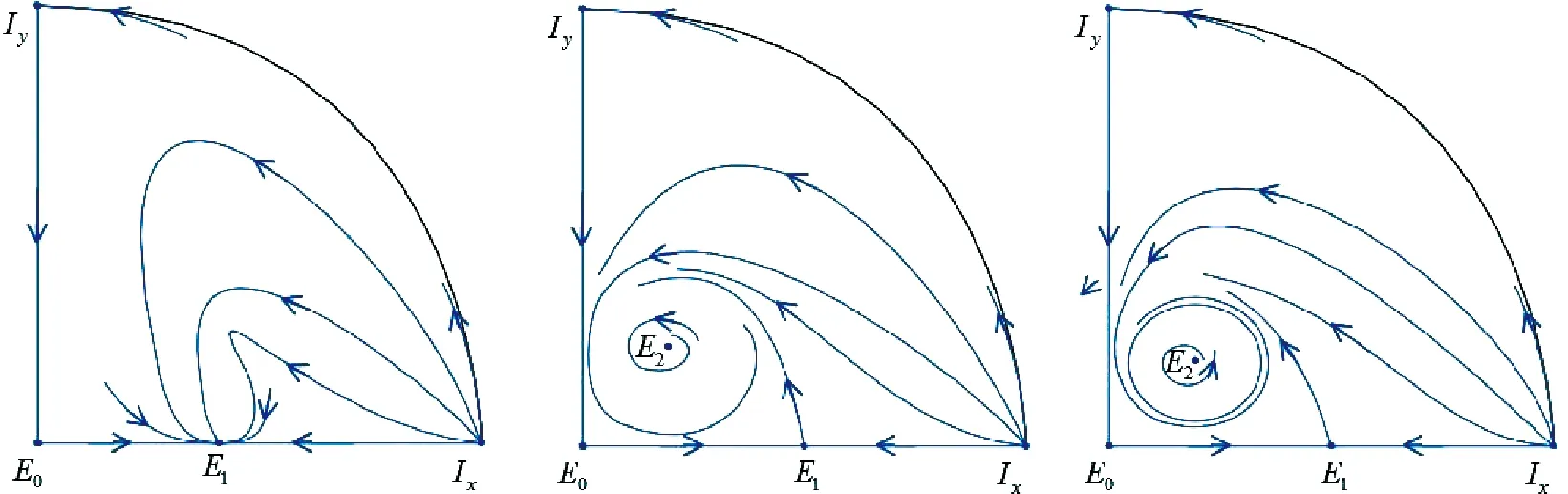
(a)α∈Λ1 (b) α∈Λ2 (c) α∈Λ3图1 系统(1)的全局相图