乙酰丙酮螯合物电子圆二色谱的理论解析

王炎

（吕梁学院 化学化工系，山西 吕梁 033001）

0 引言

作为一类由非手性结构单元形成的手性化合物，乙酰丙酮形成的过渡金属螯合物因在高性能的催化剂［1-2］和手性光电器件［3-6］、手性液晶渗染剂/掺杂物［7-9］、金属有机薄膜材料［10-12］等方面的重要应用而一直备受人们的关注［13］。但是，确定这类螯合物绝对构型的方法如X-射线衍射法［14］、Cotton效应关联法［15］和激子手性法［16］等却各有不足之处。对于配体环境复杂的手性螯合物，由于配体间的相互作用以及配体与配位中心的作用，除X-射线衍射法外，单纯地使用任一种方法来判断螯合物的绝对构型都有一定的局限性。但是，X-射线衍射法适用于固相中绝对构型的测定，不能用于液相和气相；加之符合测定条件的单晶又难以获得；在溶液和气相中，人们常用电子圆二色（ECD）、旋光色散（ORD）曲线中的Cotton效应来判定螯合物的绝对构型。近年来，随着计算机的更新换代，科学家们可以通过直接计算螯合物激发态的性质获得ECD谱，继而比照实验谱，能够较准确地确定有关化合物的绝对构型。杨翊韬等［17-19］曾系统地研究了联吡啶、邻菲罗啉络合物的电子圆二色谱，对长波区d-d跃迁和短波区激子带的特点进行了分析，纠正了文献中的一些错误。加拿大Ziegler组采用TDDFT方法研究了四种不饱和双齿配体形成的钴配合物［20-22］，提出一个分析双齿配体（包含σ轨道和π轨道）配合物ECD谱的定性框架，根据这一定性框架可以在长波区获得与实验谱基本一致的拟合谱，但乙酰丙酮配合物在短波区的拟合谱却与实验谱存在较大的差别（尤其是激子峰附近的谱带）。

为了探究这一差别的本质原因，我们选取了三种具有d6电子结构的乙酰丙酮螯合物Λ-M（acac）3（M＝Co、Rh、Ir；acac：乙酰丙酮离子的简写）进行了研究。在螯合物的ECD谱中，配体乙酰丙酮在短波区会产生相对较强的激子带，可以用激子手性法判断分子的绝对构型；中心金属离子在长波区产生较简单的d-d跃迁，利用Cotton效应也能判断分子的绝对构型。尽管从实验ECD谱可以明显看出Rh（acac）3的不是典型的激子带。但为了探究哪种方法更合适，我们通过理论计算获得了配体乙酰丙酮激子裂分对ECD谱的贡献，帮助其他研究者们根据计算所得的ECD谱选择合适的方法来确定绝对构型，尤其是包含重原子的螯合物。

1 计算方法

螯合物 Co（acac）3、Rh（acac）3、Ir（acac）3的初始结构均源自晶体数据库（CCDC）［23-25］。我们首先采用DFT/B3LYP方法对三种螯合物在乙醇溶液中的结构进行了几何优化（图1）：对于Co（acac）3使用了6-311+G（2d，p）基组，对于Rh（acac）3和Ir（acac）3采用了def2-TZVP（http：//www.basissetexchange.org）基组。在优化所获得的稳定结构的基础上，用TDDFT/B3LYP方法和同样的基组计算了三种螯合物的前100个低能激发态的性质：激发能、振子强度、旋转强度等。所有的计算都用Gaussian 09［26］程序包完成，考虑了溶剂效应（PCM模型，溶剂为乙醇）。

图1 优化后Λ-M（acac）3（M＝Co，Rh，Ir）的结构Fig.1 Optimized structure of the Λ-M（acac）3（M＝Co，Rh，Ir）

2 分析与讨论

2.1 DFT能级和Kohn—Sham轨道

三种螯合物基态的DFT能级（图2）分布相似，总体上被两个显著的能级间隙分为三组：一组占据轨道和两组能量较高的空轨道。Co（acac）3的占据轨道被三个能量间隙分成四组，随着中心金属离子周期数的增加（Rh（acac）3、Ir（acac）3），这种能量间隙变得越来越小，分组不再清晰。对于空轨道也是如此，它们之间的能隙随着中心离子周期数的增加而逐渐变小。

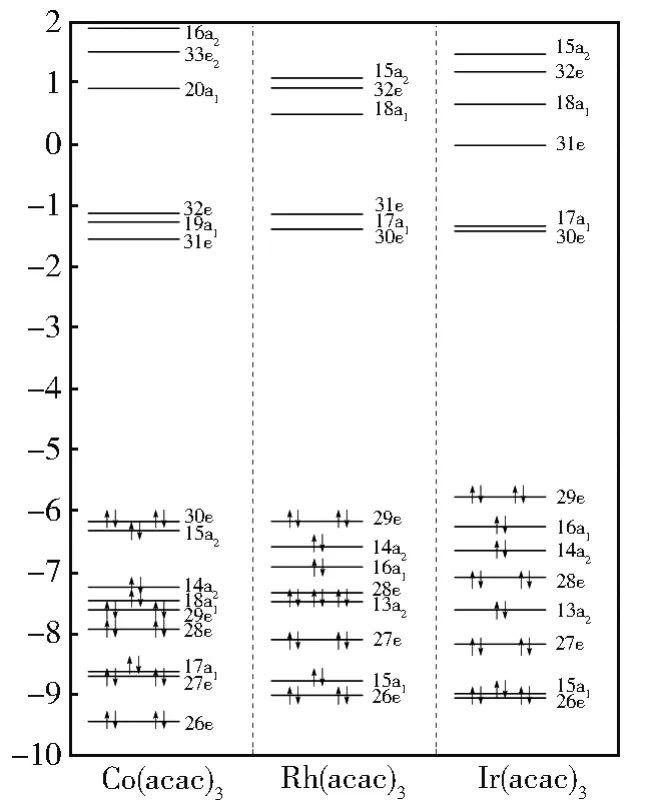
图2 Λ-M（acac）3（M＝Co，Rh，Ir）螯合物的DFT能级图（能量：eV）Fig.2 DFT energy levels of the Λ-M（acac）3（M＝Co，Rh，Ir）chelates（energy in eV）

这三种螯合物的Kohn-Sham（KS）轨道相似，图3为Co（acac）3的部分典型KS轨道。可以看出，Co（acac）3占据轨道中能量最高的30e是两个简并的轨道，除主要成分配体π轨道外，还有少量中心离子的dx2-y2、dxy与配位原子O作用形成的σM—O；能量稍低的15a2轨道，主要由配体的π轨道组成。其余占据轨道按能量由高到低依次为：n轨道、σM—O轨道。空轨道中最低空轨道为σ*M—O，能量稍高的一组为π*轨道，能量较高的一组为 σ*C—H，表现出一定的Rydberg特征。

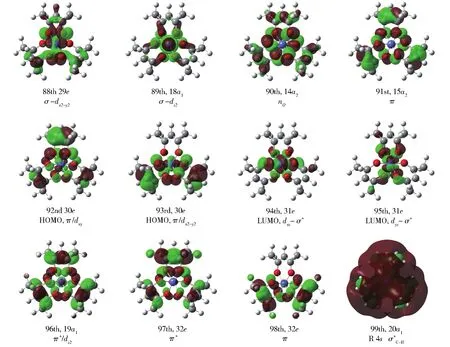
图3 Λ-Co（acac）3的KS轨道，R表示RydbergFig.3 KS orbitals of Λ-Co（acac）3，where R means Rydberg

2.2 转动强度和跃迁矩

参照实验ECD谱［15，27］（图4a）的波长范围，我们计算了三种螯合物的前100个低能单重激发态的性质。为了讨论方便，表1列出了Λ-Co（acac）3的主要跃迁的计算结果，包括跃迁波长λ、振子强度f、转动强度Rvel（速度表示）、电偶极跃迁矩μ和磁偶极跃迁矩m。其中我们最关心的跃迁只有5个，决定螯合物在长波区带形的前三个跃迁和短波区配体激子裂分的两个跃迁（285 nm附近）。

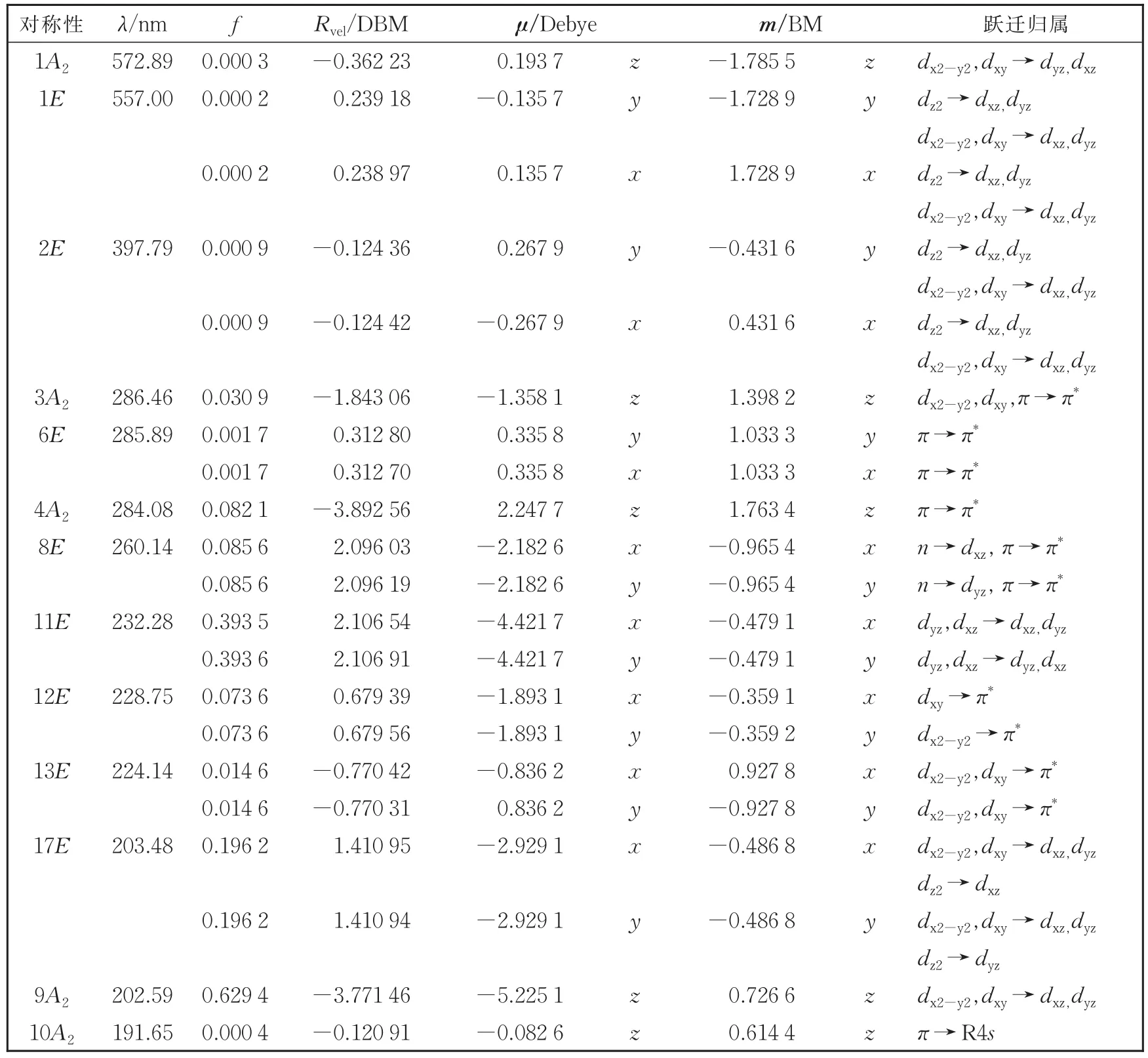
表1 Λ-Co（acac）3的主要振子强度、转动强度和跃迁矩Table1 Primary oscillator strengths，rotational strengths and transition moments of Λ-Co（acac）3

通过分析Λ-Co（acac）3的激发态性质发现：在长波区（λ＞350 nm），电子跃迁需要的能量最少，是典型的磁偶极控制跃迁（磁偶极矩达1.785 5 BM）；在短波区（λ＜350 nm），电子跃迁的种类比较复杂，主要有π→d、d→d、d→π*和π→π*等的跃迁。它们相互作用，很难简单地对短波区内的ECD带进行归属指认。其中，强度最大的是π→π*或d→d跃迁，π→π*跃迁形成的ECD谱带又在285 nm左右分裂为一对的激子带（正的E和负的A2）。在195 nm附近还存在一些弱的类Rydberg 4s的σ*C-H轨道。与Co（acac）3的激发态性质相比，螯合物 Rh（acac）3和 Ir（acac）3由于中心离子周期数的依次增加，对应的跃迁位置有一定程度的蓝移或红移，其激子带出现在260 nm附近。跃迁到类Rydberg 4sσ*C-H轨道的强度变得更强并且出现在更长的波段，其余规律都相似。

2.3 计算ECD谱与实验谱

基于上述转动强度和振子强度的计算结果，我们采用Gauss线型叠加方法，得到了三种螯合物的ECD谱（图4b）。公式中的半带宽采用经验公式，为了更好地重现实验光谱，这里的系数k取4.81×10-3（在λ＝300 nm处产生25 nm的半带宽）。

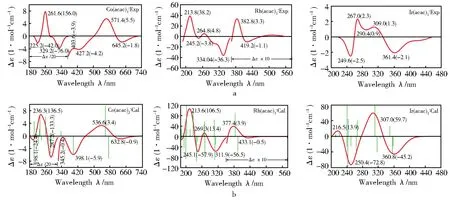
图4 Λ-M（acac）3（M＝Co，Rh，Ir）的实验图（a）、计算图（b）的对照Fig.4 Comparison of the calculated and observed ECD spectra of the Λ-M（acac）3（M＝Co，Rh，Ir）

总的来说，除了各吸收带的波长有一定的蓝移或红移外，螯合物的计算谱图与实验谱图基本一致。Ir（acac）3的计算谱和实验谱图在260 nm处相差较大，主要是因为在计算中采用赝势基组造成Ir—O键的计算值偏大，通过缩短键长（缩短了0.06 Å，Ir—O键变为1.974 2 Å）完全可以得到260 nm处的谱带（图5）。

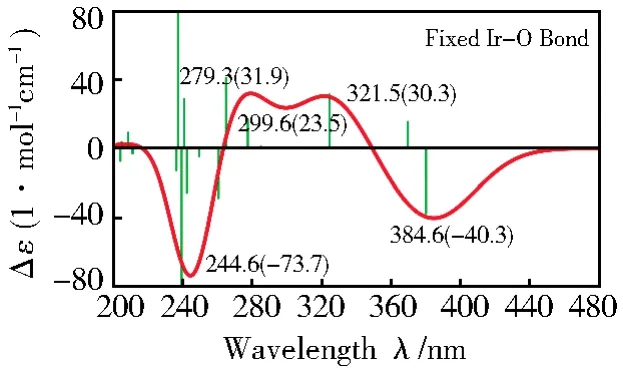
图5 固定Ir—O键长的Ir（acac）3计算图Fig.5 Calculated ECD spectrum of Ir（acac）3with the fixed Ir—O bond lengths

2.4 讨论

不饱和有机配体的ECD特征带一般是短波区的激子带，但乙酰丙酮由于配体与中心金属离子d轨道相互作用，配合物在短波区不再是单一的激子带，也不再是其特征带。而位于长波区的d-d带才是其特征带。

在λ＞350 nm的长波区，所有螯合物的第一个Cotton效应为负，判定螯合物为Λ构型，与其他由饱和双齿配体形成的ML3配合物不同（Cotton为正对应Λ构型）。其原因主要为［29-31］：这类配体中充满电子的π轨道与金属离子d轨道相互作用，增加了E跃迁的能量（与A2跃迁相比），使得能量A2＜E（饱和配体形成的配合物中的能量顺序恰好相反）。

在λ＜350 nm的短波区，π-π跃迁产生的谱带进一步分裂为一对激子带。但由于d-p耦合作用及相邻跃迁如π→d、d→d、d→π*、n→d等的影响，在ECD谱图中，原本强度相等的一对激子带变得不再对称，甚至只出现其中的一个（Rh（acac）3实验谱中的激子带由于受其他跃迁的影响变得不再典型），如此就不可能单纯地依靠激子裂分方法来判定螯合物的绝对构型，而计算谱很好地再现了激子带。

在Co（acac）3的ECD谱中，280 nm附近的激子带包含两个跃迁：11A1→61E的跃迁和11A1→41A2的跃迁。前者中纯π→π*成分占84.72%、n→d成分占6.95%；后者中纯π→π*成分占69.05%和d→d成分占19.02%，较多的d→d成分使得实验谱中激子峰的正负带强度不再相等。在Rh（acac）3的ECD谱中，260 nm附近的激子带包含了11A1→71E和11A1→41A2跃迁，前者有81.11%的纯π→π*成分和6.14%的π→d成分；后者有79.16%的纯d→d成分和25.04%的π→d成分，纯π→π*成分为0.18%，几乎为零。在Ir（acac）3的ECD谱中，260 nm附近的激子带对应11A1→51E和11A1→31A2的跃迁。前者中纯π→π*成分占86.89%、π/d→π*/d成分占7.88%；后者中纯π→π*成分占85.40%和π/d→π*/d成分占12.14%的，混杂较多的d→d成分使得正负带的强度不再对等，实验谱中看似激子峰的谱带实际是多种跃迁的综合表现。因此，按照传统的激子带的特征来判断该类配合物的绝对构型是不妥当的。

通过长波区第一Cotton效应为负可以简单正确地断定螯合物的绝对构型为Λ。通过分析计算所得的数据，螯合物激子带分裂方式为正手性（正E和负A2），可判断其构型为Λ。但由于受短波区内其余复杂跃迁的影响，在实验谱中难以准确辨认三种螯合物的激子带，更无法直观地从ECD图判断该激子分裂方式是正手性还是负手性。文献15中将这部分跃迁归属为典型的激子带并以此来判定配合物构型的方法是不妥的。相比之下，长波区磁偶极允许的d-d跃迁产生的第一Cotton效应带形简单、符号明确，可以用作绝对构型的判据。

3 结论

基于上述对螯合物计算ECD光谱的分析，我们可以得出：

（1）三种螯合物的ECD谱，除了整体上有一定程度的蓝移或红移外，各个带形和相对强度都和实验谱一致，说明TDDFT计算的ECD谱是合理的。

（2）在短波区，配体的π→π*跃迁受d-p耦合作用及其他多种跃迁n→π*、d→π*等的较强影响，激子分裂带变得复杂且不再对称，单纯依据激子带的特征直接判断对应螯合物的绝对构型是不可能的。

（3）在长波区，螯合物的ECD带简明清晰，第一Cotton效应为负，可以据此判断该类螯合物的绝对构型。