三维自适应有限时间超螺旋滑模制导律
李 军,廖宇新,李 珺
(中南大学航空航天学院,湖南 长沙 410083)
0 引 言
随着精确制导技术的不断发展,制导律除了以零化脱靶量作为目标外,往往还需要满足终端攻击角约束,才能充分发挥导弹的毁伤效果和杀伤效率。比例导引由于结构简单、所需的信息量少和易于实现的特点,被广泛应用于工程领域。虽然传统的比例导引能够实现终端零脱靶量,但对终端攻击角约束却很难达到满意效果[1]。
随着现代控制理论的发展,为了解决终端攻击角约束问题,在原有制导律设计思想的基础上,进行将先进控制理论应用于带攻击角约束的制导律设计的相关研究,如最优制导律[2-4]和微分对策制导律[5-6]等。由于滑模控制能使系统快速趋于稳定,且控制器具有形式简单和对外界干扰强鲁棒性等优点,因而广泛应用于带攻击角约束的制导律设计。文献[7]针对具有终端攻击角约束的导弹拦截问题,设计了一种基于扩展状态观测器的快速终端滑模制导律,该制导律使拦截弹道更优,同时解决了视线角速率只能渐进收敛到零的问题,有效缩短了打击时间。文献[8]设计了一种基于非线性干扰观测器的快速终端滑模制导律,将目标加速度视为未知的有界外部干扰,同时在滑模面中引入非线性干扰观测器估计并补偿实际的外部干扰;针对线性滑模制导律存在视线角收敛时间较长现象,通过快速终端滑模控制策略进行解决,但造成系统状态在平衡点附近的奇异问题。文献[9]针对导弹拦截存在攻击角需求和非线性滑模制导律的系统奇异问题,利用动态面法,设计了一种考虑弹体动态特性的非奇异有限时间制导律,满足了终端攻击角约束和系统在有限时间的收敛,但目标机动引起的未知干扰会造成制导指令较强的抖振。
抑制抖振现象,可在制导律的鲁棒项中利用饱和函数代替符号函数解决。文献[10-11]针对攻击角约束要求,分别提出了固定时间收敛制导律和有限时间收敛制导律。由于滑模变结构中含有开关函数,控制量进行高频切换时,会在实际系统中引起制导指令的抖振。因此文献[10-11]通过饱和函数法减小制导指令抖振引起的弹体抖动,但这使系统轨迹稳定在滑模面附近,从而削弱了制导律的鲁棒性。为了提高系统控制精度,可以采用高阶滑模控制来抑制抖振,高阶滑模在消除相对阶限制的同时还增强了系统对干扰的鲁棒性[12]。高阶滑模控制方法中的超螺旋(super-twisting,ST)算法,具有特殊的嵌套结构,不需要滑模变量的一阶导数信息。ST算法的实际控制变量在相对阶为1的控制系统中,不存在高频切换,因此减少了因控制量切换引起的抖振现象,多种利用ST算法抑制抖振的制导律相继被提出[13-15]。然而,ST算法对系统的不确定性较为敏感,当外部干扰上界未知时,过高的估计干扰上界会导致过大的控制增益,使得系统不确定性增大,降低闭环系统的鲁棒性。外部干扰参数的自适应能够实时在线估计干扰上界,从而降低控制增益,减小系统抖振,保证系统具有良好的控制性能,因此多种自适应制导律相继被提出[16-18]。
由于导弹拦截目标的真实情形发生在三维空间,因此三维制导律相较于二维制导律更适合真实情形。同时,导弹还必须具有拦截高速机动目标的能力,才能满足作战节奏快速性和战场复杂性的需要。针对导弹拦截的真实情形,文献[19-21]分别设计了相应的三维滑模制导律。为了达到更好的拦截毁伤效果,在进行零化脱靶量精准制导的同时,制导律还需要满足终端攻击角约束。
针对终端攻击角约束的导弹拦截机动目标制导问题,本文在目标加速度未知的前提下,建立了非解耦且在有限时间内收敛的三维自适应制导律,实现了以固定终端攻击角的精准拦截制导,同时解决了目标未知机动对制导精度的影响。首先,根据弹目三维相对运动关系,建立了导弹-目标相对运动质点模型。然后,基于改进ST算法和非奇异快速终端滑模,设计了有限时间ST滑模制导律(finite-time ST sliding mode guidance law,FSTSMGL)。此外,为了解决目标机动加速度带来的外部干扰上界未知问题,将FSTSMGL的干扰项进行实时在线的参数自适应估计干扰上界,提出一种自适应FSTSMGL(adaptive FSTSMGL,AFSTSMGL),实现了扰动上界的自适应增益估计。同时,对闭环系统有限时间收敛进行证明,并给出了系统的收敛时间。最后,为了验证AFSTSMGL制导性能的优越性进行了对比仿真。结果表明,AFSTSMGL具有更强的鲁棒性、更快的收敛速度和更高的制导精度。
1 系统模型及相关引理
1.1 系统模型
为了研究三维空间中机动目标的导弹拦截制导问题,在地面惯性参考坐标系OIXIYIZI中,将导弹和目标均视为质点,同时构建目标速度坐标系OTXTYTZT、导弹速度坐标系OMXMYMZM和视线坐标系OMXLYLZL,则弹目三维相对运动关系如图1所示。

图1 弹目三维相对运动示意图Fig.1 Three-dimensional relative motion diagram of missile and target
导弹速度关于OMXLYLZL坐标系的速度倾角和速度偏角分别为θM和φM,目标速度关于OMXLYLZL坐标系的速度倾角和速度偏角分别为θT和φT,则根据图1中坐标系可将导弹-目标相对运动质点模型[22]描述为
(1)

导弹和目标的质点运动模型[22]分别可以描述为
(2)
(3)

根据式(1)~式(3),视线角的二阶微分方程可描述为
(4)
当导弹与目标的相对速度小于零时,由式(4)可知合适的俯仰加速度aZM和偏航加速度aYM可以使视线角速率收敛至零。
基于上述耦合模型进行制导律设计,假设θM,φM≠±π/2,|aYT|≤a1,|aZT|≤a2。其中,∀t≥0时,a1和a2分别为目标加速度在偏航和俯仰方向上的上界,令θLf和φLf分别为期望终端视线倾角和期望终端视线偏角,状态变量x1=[x11,x12]T=[θL-θLf,φL-φLf]T,则基于视线角误差的二阶系统状态方程为
(5)
(6)

为保证导弹能以θLf和φLf精准拦截目标,应通过设计光滑的制导律u,让系统在未知干扰M存在的情况下,满足视线角速率和视线角误差在有限时间内收敛到零。
1.2 相关引理
引理 1[23]如果存在一个连续正定的函数V(t):Rn→R,当∀t>t0时满足不等式:
(7)
式中,t0为初始时间;α,β>0且0 (8) 引理 2[24]如果在区间Ω:0∈int(Ω)存在一个连续的函数V(x):Rn→R,且满足不等式: (9) (10) 为了使导弹能以期望的攻击角度成功拦截目标的同时还可以避免系统奇异问题,在文献[25]的启发下,选取多变量非奇异快速终端滑模面如下: S=[S1,S2]T=x1+K1|x1|αsign(x1)+ (11) 式中,K1和K2>0为正实数;1<β<2,α>β, 式(11)对时间求导,可得 (12) 快速趋近律由文献[26]的改进ST思路启发,表达式为 (13) 式中,实数矩阵K3,K4,K5均为2阶正定对角阵。则式(5)、式(12)和式(13)联立可得FSTSMGL表达式为 (14) 当外部干扰上界未知时,过高地估计干扰上界会导致过大的控制增益,使得系统的不确定性增大,闭环系统的鲁棒性降低。为了解决目标机动加速度带来的外部干扰M上界未知的问题,利用参数自适应增益实时在线估计干扰上界,可得AFSTSMGL的表达式为 (15) 式中,K3(t)和K4(t)为干扰项M的自适应增益估计;K6,K7,Ω1,η1,μ1均为正实数。 定理 1令M=[M1,M2]T,当存在Mmax使Mi≤Mmax成立时(其中Mmax为正实数,即干扰项M有界),若选用趋近律式(13)、滑模面式(11)和制导指令式(15),则 (2) 滑模变量S在有限时间内收敛到零; (3) 系统的状态变量x1,x2在有限时间内收敛到零。 在式(5)中成立。 证明将式(5)和式(15)代入式(12)中可得 (16) 令Di=[di1,di2]T=[|Si|1/2sign(Si),Wi]T,定义一个子空间vi={(Si,Wi)∈R2|Si=0},则在不包含vi的所有空间内,Di的时间导数可表示为 (17) 式中, Kj= diag{Kj1,Kj2} 趋近阶段考虑如下Lyapunov函数 (18) 式(18)对时间求导,同时令Mi=r(t)sign(Si),0≤r(t)≤Mmax,可得 (19) 式中, 将式(19)变换为 (20) (21) (22) (23) -K3i-2K3ir<0 (24) 2K5i(K3i+1)|di1|(K3i+2K3ir)- (25) 由式(22)和式(23)可得 (26) (27) 式(24)显然成立。令 (28) 因为a1<0,所以r<-a2/2a1时,f(r)是单调递增的,故当-a2/2a1>0且f(0)≥0时,∃r∈(0,-a2/2a1)使得f(r)>0成立,即Hi2为负定矩阵的充分条件为 (29) (30) 式(29)显然成立。由式(26)和式(29)可得 (31) 将式(19)变换为 (32) (33) 因为 所以由式(32)可得 (34) 式中,λmin{·}和λmax{·}分别为矩阵的最小和最大特征值;‖·‖为欧式范数。 (35) 考虑如下Lyapunov函数 (36) 将式(36)对时间求导可得 (37) (38) 由式(35)和不等式(|a|p+|b|p)1/p≤|a|+|b|,p>1可得 -(ρ1V1/2(D)+ρ2V(D)) (39) 式中,ρj=min{ξi j|i=1,2}。 根据引理1可知,滑模变量S在有限时间内收敛到平衡点0,收敛时间TS为 (40) 式中,D0为零时刻D的初值。 由S=0可知: x1+K1|x1|αsign(x1)+K2|x2|βsign(x2)=0 (41) 令Z[a]=|Z|asign(Z),则式(41)可化简为 (42) 根据引理2可知,系统状态变量x1和x2在有限时间内可以收敛到平衡点零,即有限时间内视线角误差和视线角速率可以收敛到零。状态变量收敛时间Tx和系统收敛时间T分别为 (43) (44) 所以式(5)的状态变量x1和x2将在T时间内收敛到平衡点0。 证毕 本节通过高速机动目标弹道拦截仿真,验证制导律AFSTSMGL的有效性和优越性。仿真参数设置为:初始弹目距离R(0)=6 000 m,初始视线倾角θL(0)=30°,初始视线偏角φL(0)=0°,导弹和目标初始速度倾角θM=10°、θT=20°,导弹和目标初始速度偏角φM=10°、φT=180°,目标初始速度VT=300 m/s,导弹初始速度VM=600 m/s,导弹初始位置xM=[0,0,0]T,导弹最大过载aZM=aYM=25g,重力加速度g=9.8 m/s2,仿真步长为0.001 s,当弹目相对距离|R|<1 m时,仿真结束。 同时为了更全面地分析AFSTSMGL的制导性能,在仿真中与FSTSMGL和非奇异终端滑模制导律[22](non-singular terminal sliding mode guidance law,NTSMGL)展开不同期望终端视线角的制导对比。NTSMGL表达式为 (45) 由于制导律鲁棒项的符号函数会引起抖振问题,所以根据饱和函数法缓解抖振,将式(45)中sgn(S)替换成如下函数: (46) AFSTSMGL的参数设定为K1=0.05,K2=1,K5=diag{5,10},K6=18,K7=14.4,α=5,β=8/7,μ1=0.05,Ω1=0.01,η1=0.1;FSTSMGL的参数设定为K1=0.05,K2=1,K3=diag{0.37,0.46},K4=diag{0.01,0.02},K5=diag{10,10},α=5,β=8/7;NTSMGL参数设定为α=15/13,β=1.1,k=0.01,h=0.1,H=diag{0.3,1}。 考虑如下3种不同的期望终端视线角情形: (1) (θLf,φLf)=(25°,5°) (2) (θLf,φLf)=(35°,5°) (3) (θLf,φLf)=(35°,10°) 图2 三维拦截轨迹Fig.2 Three-dimensional interception trajectory 图3 制导指令Fig.3 Guidance instruction 图4 视线角Fig.4 Line-of-sight angle 图5 视线角速率Fig.5 Line-of-sight angle rate 图6 滑模面Fig.6 Sliding surface 表1 以期望终端视线角1拦截目标的仿真结果Table 1 Simulation results of intercepting target with expected 表2 以期望终端视线角2拦截目标的仿真结果Table 2 Simulation results of intercepting target with expected terminal line-of-sight angle 2 表3 以期望终端视线角3拦截目标的仿真结果Table 3 Simulation results of intercepting target with expected terminal line-of-sight angle 3 综上可知,目标混合机动情形下,针对不同终端攻击角需求,所设计的AFSTSMGL脱靶量较小,终端视线角误差和系统收敛特性明显优于其他方法,具有良好的鲁棒性、较广的终端攻击角适应范围和更高的拦截精度。 针对具有攻击角约束的制导问题,基于非奇异快速终端滑模面和改进ST算法,设计了一种FSTSMGL,既避免了抖振,又保证了系统在有限时间内收敛。 针对外部干扰上界未知的情况,利用参数自适应增益实时在线估计干扰上界,设计了一种AFSTSMGL,能够满足对机动目标的精准拦截和终端攻击角约束要求。自适应律的形式简单,不影响系统有限时间内的收敛性能,提高了闭环系统的鲁棒性。 通过与FSTSMGL和NTSMGL在3种不同期望终端视线角下的仿真对比,验证了本文设计的AFSTSMGL制导性能的优越性、有效性和鲁棒性,提高了制导的打击精度和终端攻击角约束的控制精度。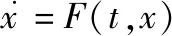
2 制导律设计及系统稳定性分析
2.1 AFSTSMGL设计
K2|x2|βsign(x2)
2.2 有限时间收敛性能分析



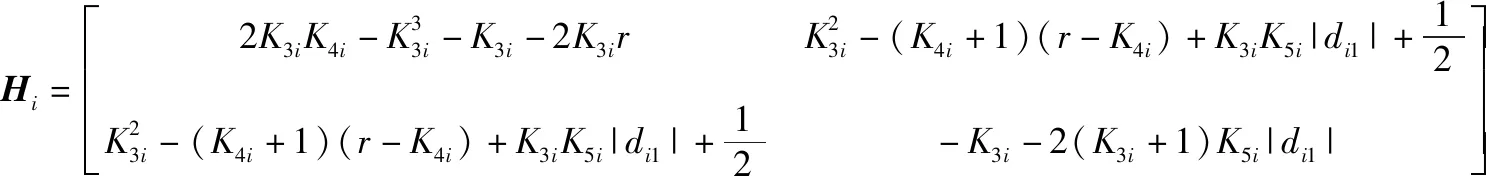
(K3iK5i|di1|+(K4i+1)r)2>0


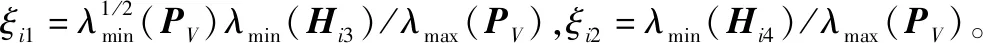
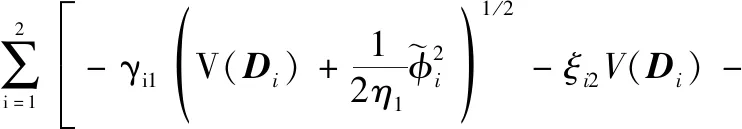


3 仿真分析











4 结 论

