电动舵机极限环机理分析和抑制措施

周志明,林 凡,姚晓先,宋晓东

(北京理工大学宇航学院,北京 100081)

0 引 言

舵机作为导弹上的执行机构,通过跟踪制导系统发出的制导指令来调整舵片位置,从而改变导弹姿态和过载,控制导弹飞行。电动舵机作为一种比例式舵机,具有良好的伺服跟踪性能,广泛应用于各类型导弹上。

目前,国内外一般将舵机模型简化为二阶系统[1-4],其中不仅未考虑舵机传动过程中的摩擦作用,也没有考虑传动机构的非线性因素。为更精确地描述舵机真实的状态,更多学者对舵机模型中诸如控制死区、传动间隙、摩擦力等因素进行考虑,建立了更接近舵机实际状态的模型[5-8]。

舵机间隙属于典型的机械传动间隙,针对机械传动过程中的间隙,Nordin[9]等系统地阐述了不同的建模方法以及多种线性和非线性控制策略。针对传统间隙补偿方法,Dean[10]等人通过实验表明间隙逆模型补偿方法容易导致系统振颤。应用状态反馈极点配置的方法,Yang[11-12]等抑制了双惯量伺服驱动系统中传动间隙诱导的极限环,但是难以同时保持系统的伺服性能。目前,对于间隙非线性的分析多采用基于描述函数法的思路[13-17]或者基于李雅普诺夫的分析方法[18-21]。其中,模型自适应控制[22-25]和模型预测控制[26-28]研究更为广泛,但是多为理论层面分析,实际系统中应用较少。另外,工程上常采用多电机驱动消除间隙的影响,但是理论分析较少,针对多电机驱动系统,控制系统稳定性和电机电压控制等问题都有待进一步深入研究[29-30]。

本文建立了电动舵机包含传动间隙的非线性动力学模型,并且创新性地考虑了减速器刚度模型,提出了一种在工程上易于实践的负反馈力矩的方法,分析了该负反馈力矩对系统性能的影响,给出了该反馈系数的选取准则,并且仿真验证了该方法可以在保证不影响舵机伺服性能的情况下有效地抑制极限环的产生,对工程实践具有一定的指导意义。

1 电动舵机模型

一般的电动舵机传动结构示意图如图1所示。

图1 电动舵机传动结构示意图Fig.1 Structure diagram of electric actuator

电动舵机的工作原理是电机在控制器的控制下,带动减速器,驱动舵片旋转,反馈电位计将舵片位置反馈给控制器。舵机传动过程中,减速器并非一个刚度无限大的传动结构,而是电机带动减速器转动,发生形变从而对舵片施加相应的传动力矩。由于减速器一般为金属制作,刚度很大,产生的形变角相对于舵机系统需要相应的跟踪指令来说,可以忽略不计。但是对于一个有传动间隙的舵机系统来说,考虑减速器刚度有助于分离舵片的受力,从而便于分析舵机在传动非线性下的运动模态。针对传统的舵机建模未考虑减速器刚度和舵片所受摩擦力的问题,本文建立如下模型。

电机的转矩方程为

(1)

式中,Jm为电机转轴转动惯量;φ为电机转轴的转角;Te为电机的电磁驱动力矩;Ts为减速器形变产生的负载力矩。舵片的转矩方程为

(2)

式中,Jl为舵片转动惯量;δ为舵偏角;k为舵片摩擦力矩系数,这里认为在一定的小角度范围内，舵片所受的阻力力矩与舵片的运动速度成正比。减速器形变产生的扭矩方程为

Ts=Ks(φ-Nδ)

(3)

式中,Ks式为减速器等效刚度;N为减速器的传动比。电机的电压方程为

(4)

式中,U为输入电压;L为电感;R为电阻;E为反电动势,反电动势可以表示为

(5)

式中,Ke为反电动势系数。忽略电感和动态过程,电机的驱动力矩和电流成正比,其可表示为

Te=KmI

(6)

综合以上各式可以得出

(7)

式中,

B(s)=(JmRs2+KeKms)(Jls2+ks+KsN2)+KsR(Jls2+ks)

当不考虑舵片摩擦力,即k=0,且减速器刚度足够大时,式(7)可以化简为

(8)

式(8)即是文献[2-4]中所采用的舵机模型,当考虑舵片摩擦力和减速器刚度时,系统传递函数变为四阶。考虑舵机系统常用的PD控制器及传动中的间隙，用死区模型来分析舵机传动中的间隙。将所有的间隙都等效到减速器输出端到舵片之间,舵机的传动结构框图如图2所示。

图2 舵机传动结构框图Fig.2 Block diagram of actuator’s transmission structure

图3 简化的舵机结构框图Fig.3 Block diagram of simplified actuator

其中,

θs为减速器形变扭转角;θd为减速器末端与舵片的差分角,当满足θd=φ-Nδ≥b时,传动齿轮和负载舵片处于正向啮合,电机带动舵片正向运动,当满足θd=φ-Nδ≤-b时,传动齿轮和负载舵片处于负向啮合,电机带动舵片负向运动。图3中N(A)为死区非线性的描述函数：

(9)

式中,A为输入信号幅值;2b为死区大小。线性部分的传递函数为

G2(s)=(Kp+Kds)Gp(s)H(s)

(10)

2 极限环求解

根据极限环存在性定理,假设本文中的舵机模型存在极限环振荡,则应该有

(11)

注意到死区的描述函数是关于输入幅值A的单值函数,值域是实数,所以其负倒描述函数的图像必定位于实轴上。假设系统存在极限环,则极限环的频率必定使得线性部分的传递函数的虚部为零。即

ImG2(jω)=0

(12)

不考虑舵片摩擦力时,即k=0时,可解得

(13)

ReG2(jω)<-1

(14)

可求得

(15)

式中,

当考虑舵片所受摩擦力,即k≠0时,类似前述方法,假设存在极限环,忽略微分系数的影响,可求得极限环振荡频率为

(16)

将所求的交点频率代回实部,并且求解ReG2(jω)<-1成立的条件,其解析表达式过于冗长复杂,无法从中提取信息来分析系统极限环存在条件。但是通过分析和数值仿真可知,相比于不考虑舵片所受摩擦力的模型,考虑摩擦力作用的模型相当于系统添加了额外的阻尼作用,该阻尼作用可以一定程度上可抑制极限环的产生。但是由于摩擦力一般较小,其阻尼作用有限,所以在较大的控制系数下,系统依然会产生极限环振荡。然而过小的控制系数会导致伺服系统跟踪性能变差,并且出现严重的“平顶”现象。

3 极限环的抑制措施

本文提出一种负反馈力矩方法来抑制传动间隙的影响。在舵片上添加一个负反馈力矩,其大小正比于舵偏角,即

Tf=-fδ

(17)

工程上可以在图1中减速器与舵片的连接处加装一个紧固发条,或者在舵片两侧各加装一个弹簧,并且连接到舵机壳体上,由于舵机指令通常较小,可近似认为舵片偏转后产生的回零力矩与偏转角度成正比。因此,舵片的转矩方程变为

(18)

(19)

特征根为

(20)

在引入力矩负反馈后,不仅改变了舵机在间隙区间的运动状态,也改变了舵机系统的增益和零极点。引入反馈后,从舵片输出到指令的闭环传递函数为

(21)

式中,

A(s)=KsNKm(Kds+Kp)
B(s)=(Jls2+ks+f+KsN2)(JmRs2+KmKes)+
KsR(Jls2+ks+f)+KsNKm(Kds+Kp)

当f=0时,不管系统的控制参数取值如何,系统的稳态增益为1。当f≠0时,系统的稳态增益变为

(22)

可以看出,随着f增大,系统的静差增大,为保证伺服系统的跟踪性能,f有一个上限值,实际舵机系统中,可取f使得系统稳态误差小于3%。可以看到,引入的力矩负反馈对系统零点没有影响,对系统极点也基本没有影响,从而保证了系统的伺服跟踪性能。然而,要保证负反馈力矩作用远远大于摩擦力作用,需要在量级上满足f≫k,这就需要在抑制振荡和系统稳态增益之间取折中。

4 仿真验证

本文以某型小型电动舵机为例,仿真时使用的参数如表1所示。仿真中没有考虑反馈电位计测量噪声。先验证本文预测的极限环的准确性,采用simulink搭建图1中仿真模型,不考虑舵片摩擦力,令Kd=0,设置不同的比例参数,在给定参考信号下观察舵偏角输出响应如图4所示。对上述舵机响应进行快速傅里叶变换,进行频谱分析可得,当Kp=10时,舵机响应包含频率为1 Hz的基波和频率为47.6 Hz的谐波,当Kp=40时,舵机响应包含频率为1 Hz的基波和频率为101.5 Hz的谐波。其中1 Hz信号为舵机所响应的指令信号,高频谐波为传动间隙引起的极限环振荡。由式(13)所预测的极限环频率分别为57.4 Hz和114.9 Hz,与实际仿真结果有一定的偏差。这是由于描述函数法本身就是一种近似方法,用非线性环节对输入信号响应的一次谐波近似代替其真实响应,但是对于工程上预测和避免极限环振荡依然具有指导意义。考虑舵片所受摩擦力情况下,令k=0.001 Nm·s/rad,Kd=0,设置不同的比例参数,在给定的参考信号下观察舵偏角输出响应如图5所示。当Kp=20时,可以看到,系统没有产生振荡,但是出现了“平顶”现象,原因在第3节已有阐述。另外,较小的控制参数导致舵机的跟踪性能下降,相位滞后明显。为减小平顶的宽度和时间,提高比例系数至Kp=200。可以看到,系统出现了极限环振荡,通过快速傅里叶分析可得其振荡频率为74 Hz,通过式(16)求得的极限环频率为94 Hz。

表1 仿真参数表Table 1 Parameter used in the simulation

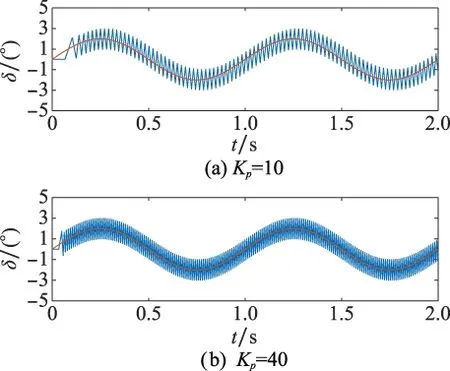
图4 不同比例系数下舵机响应Fig.4 Response of the actuator under different coefficients

图5 考虑摩擦力下不同比例系数舵机响应Fig.5 Response of the actuator under different coefficients with the friction considered

与图5对比,在Kp=200时引入力矩负反馈,在保证系统静差3%的条件下,取f=0.2 N·m/rad,观察舵机输出以及减速器和舵片的差分角如图6所示。

图6 引入负反馈后的舵机响应和差分角的变化Fig.6 Response of the actuator and the differential angle under the feedback moment

可以看到,在引入力矩负反馈后,系统没有产生极限环振荡,与第3节分析吻合。当舵片穿越零位时,由于反馈力矩的方向改变,舵片运动进入间隙,并且迅速稳定。从舵片与减速器差分角θd可以看出,舵片与减速器始终一侧啮合,当穿越间隙时,由于负反馈力矩的存在,舵片以较大的速度快速穿越间隙,啮合上另一侧。由于负反馈力矩的作用,舵片无法到达指令峰值,但是通过合理的选取反馈系数可以使得该静差在可接受的范围内。

5 结 论

本文推导了包含传动间隙的电动舵机模型,分析了系统存在极限环的条件,并且给出了极限环振荡的频率和幅值特性。分析表明,在没有摩擦力影响情况下,系统极限环的频率与比例系数的二分之一次方成正比。系统中的摩擦力对极限环有抑制作用,分析和仿真结果解释了实际舵机系统测试过程中出现“平顶”现象的原因。

引入负反馈力矩机制后,有效地抑制了系统极限环振荡。分析和仿真结果表明,负反馈力矩使得舵片与减速器之间的差分角迅速切换并且稳定,使得舵片与减速器平稳地穿过间隙,从而抑制了极限环振荡。负反馈力矩系数对系统稳态误差的有一定的影响,给出了系数选取准则。