两种群捕食者-食饵模型解的整体性态

闫 莎

(陕西理工大学 数学与计算机科学学院， 陕西 汉中 723000)

种群生态学是生态学的一个重要分支，在生态系统中，捕食者-食饵模型的稳定性是大家广泛关注的问题[1-5]。文献[6]对于两种群食物链模型

(1)

的常微分方程组形式，即空间分布均匀的情况做了研究。这里P1、P2分别表示捕食者、食饵种群的密度，h是P1的消化系数，C1是P1的捕食率，B1是P1的转化率，D是P1的死亡率，r和k分别是P2的内禀增长率和环境容纳量。

式(1)仅仅反映了该种群模型常微分方程的情形P1与P2的密度仅依赖于时间的变化而变化,但是在现实的生态圈中,生物种群在其生存区域内具有迁移的本能,考虑到空间位置对种群密度的影响,对式(1)加入扩散项,主要研究式(1)对应的弱耦合反应扩散系统解的整体性态。

(2)

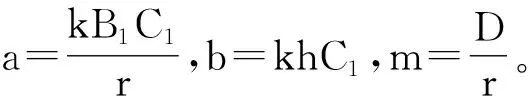
(3)

本文借鉴文献[7]的方法，主要讨论式(1)对应的弱耦合反应扩散模型，即式(3)解的整体性态。

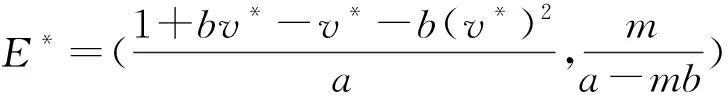
(4)

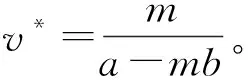
1 模型解的一致有界性

由文献[8]易知,∃T>0,使得式(3)在[0,T]上存在唯一解。

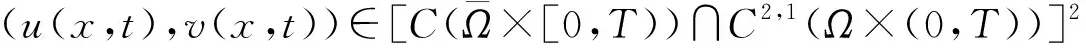
证明设(u,v)是式(3)在初值u(x,0)=u0≥0及v(x,0)=v0≥0时的解,由文献[9]中的比较原理易知,当(x,t)∈Ω×[0,T)时,(u,v)≥0。

对式(3)的第二个方程应用比较原理得

v(x,t)≤M1≡max{‖v(0)‖L∞(Ω),1}，

令Z=u+v,则

所以

由文献[10]可知,存在依赖于‖u0‖∞和‖v0‖∞及式(3)系数的正常数M,使得

‖Z(x,t)‖L∞(Ω)≤M，

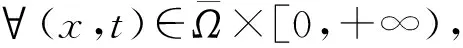
2 模型非负平衡点的局部渐近稳定性

定理2 (a) 式(3)的平凡平衡点E0无条件不稳定；

(c) 式(3)的正平衡点E*无条件不稳定。

(a) 令D=diag(d1,d2),L=DΔ+Fu(E0)=DΔ+{aij},其中E0为平凡平衡点，式(3)在E0处的线性化矩阵为

J(E0)的特征方程为φ(λ)=(λ-1)(λ+m)=0。因为φ(λ)=0有正根λ1=1,所以式(3)的平凡平衡点E0是无条件不稳定的。

(b) 令D=diag(d1,d2),L=DΔ+Fu(E1)=DΔ+{aij},其中E1=(0,1),式(3)在E1处的线性化矩阵为

(c) 令D=diag(d1,d2),L=DΔ+Fu(E*)=DΔ+{aij},其中E*为正平衡点,式(3)在E*处的线性化矩阵为

J(E*)的特征方程为

φ(λ)=λ2+Aλ+B=0,

其中A=-(a11+a22),B=a11a22-a12a21。

经初等计算可得

要使φ(λ)的两个根λ1、λ2的实部均为负,由文献[11]可得,必有Δ1>0,Δ2>0，即a11<0,a22<0,又a11<0等价于

(5)

3 模型半平凡平衡点的全局渐近稳定性

由于式(3)的平凡平衡点E0(0,0)及正平衡点E*均是无条件不稳定的,因此,下面只讨论式(3)的半平凡平衡点E1=(0,1)的全局渐近稳定性。

引进如下结论：

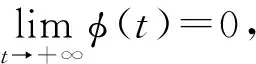
设(u,v)是式(3)唯一的正解,由定理1和文献[13]中的定理A2知,∀t0>0,当t≥t0时有

(6)

(7)

其中α∈(0,1),C是不依赖于t的正常数。

定理3 当a

证明定义Lyapunov函数

设(u,v)是式(3)的解,则(u,v)在任意正时刻为正。当t>0时,有

由式(6)、(7)及定理1可得,式(3)的解有界,式(3)中u、v-1的导数均有界,结合引理1得

(8)

由u,v≤C有

仍由式(6)、(7)知g′(t)在[t0,+∞)(t0>0)有界。由引理1知,当t→+∞时g(t)→0,即

由Poincare不等式得

(9)

由式(8)、(9)得

(10)

(11)

当t=tm,由式(3)的第二个等式得

(12)

结合式(8)、(11)、(12)得

(13)

由式(6)、(7)知,存在子列{tm}、非负函数wi∈C2(Ω),使得

由式(8)、(13)得w1=0,w2=1，即有

(14)

(15)

由式(14)、(15)以及E1的局部渐近稳定性得到,当a