基于spark平台的供电煤耗并行回归预测

李偲希，白全生，舒畅，肖祥武

(湖南大唐先一科技有限公司大数据事业部，湖南 长沙 410000)

随机森林算法是目前应用较为广泛的机器学习算法之一[1]。文献[2]表明随机森林算法在121个数据集上的179种分类算法的分类性能测试中表现最优。近十年来，随着电力大数据的发展，随机森林算法在电力行业发挥了巨大作用。文献[3]利用随机森林算法抗噪和适应能力强的特点，提出了一种计算漏报率的随机森林集成投票算法模型，提高了电机承轴故障诊断的准确率。文献[4]将模糊聚类与随机森林相结合所建立的模型，在电力系统短期负荷变化的预测中有良好的表现。随着随机森林算法的不断实践，其缺陷也逐渐被重视，很多学者对其不足之处提出了改进方案，文献[5]提出了一种基于欠采样和合成少数类过采样技术相结合的优化算法，来改善数据不平衡问题，有效提升了随机森林在非平衡数据集上的性能。文献[6]设计并实现了采用spark分布式存储计算技术的基于spark的随机森林算法，大大提升了运算速度。另一种基于决策树的集成算法——梯度提升决策数[7]算法(以下简称GBDT算法)，也是工业领域较为常用的算法。文献[8]提出了一种基于GBDT模型的交互稳定性评估方法，为串联结构系统在电能质量分析、优化运行等方面提供了方法支持，而文献[9]则在研究了现有的GBDT并行算法后提出了基于二元相关性和梯度提升决策树集成学习的多标签分类方法，提升了电力ICT系统复杂故障类型的多标签分类的准确率。随机森林算法与GBDT算法虽然在故障诊断、电力负荷预测等工业场景中应用较为广泛，但是对于火电厂海量且冗杂的能耗数据中是否也有同样优异的表现还有待研究。因此，本文的目标在于比较两种算法在核心原理、参数调整和回归模型效果上的差异，并且运用大数据平台中的实时数据进行分析，分别建立基于spark平台的随机森林和GBDT并行算法的回归模型，比较两种模型对电厂煤耗的预测效果。

1 Spark框架

Spark[10]是基于内存计算的大数据分布式集群框架，它在海量数据集上的计算性能十分高效。Spark的核心部分则是弹性分布式数据集(简称RDD)[11]，它在群集的多台节点上对数据进行分区。RDD支持两种操作：转换和操作。转换算子只记录转换的过程，而只有当触发操作算子时才能真正执行程序。由于只有在真正需要将结果写入RDD时才会执行以上操作，因此计算效率便得到了很大的提升。本文主要通过基于spark平台的随机森林和GBDT算法建立回归模型，并对模型的预测效果进行比较分析。

2 决策树算法介绍

2.1 决策树算法

决策树[12]是一种用于分类和回归的树结构。分类树用于对离散标签数据进行分类。如果目标变量的值是连续型，那么该类决策树称为回归决策树。

比较常见的决策树算法有ID3，C4.5，分类回归决策树(以下简称CART决策树)等[13]，前面两种算法仅支持分类问题，而CART决策树既可用于分类，也能解决回归问题。

2.2 分类回归决策树

分类回归决策树是一棵二叉树[14]，每次只将数据切分成两部分。CART分类树的中心思想是自上而下从根节点开始建立节点，每一个节点处选择基尼指数[15](又叫基尼不纯度)最小的特征进行分割，CART回归树采用样本最小平方误差作为节点分裂的依据。

CART决策树算法非常容易出现过拟合问题，导致泛化能力不强，此外，在寻找最优决策树时容易陷入局部最优。因此，在处理实际问题时，运用单一的回归树是远远不够的。而随机森林算法以及GBDT算法在回归树的基础上，结合bagging[16]和 boosting[17]两种集成学习方法进行改良和升级，大大提高了其泛化能力。

3 随机森林算法原理

随机森林算法是一种基于bagging方法的并行式集成学习算法[18]。Bagging方法的基本原理是对于一个大小为M的总样本集，通过bootstrap自助采样法[19]得到T个大小为M的样本子集，通过T个样本子集分别训练生成T个弱学习器[20]，bootstrap方法简单来说就是一种有放回随机抽样。最终进行集成时，如果是分类问题则采用投票法，若为回归问题则采用平均法。之所以被称为随机森林，是因为首先它是由多个决策树集成的，并在此基础上引入了随机特征的选取。随机森林中子树的每一次分裂过程并未用到所有的特征，而是从待选特征中随机选取一定的特征，再从随机选取的特征中找出最优的特征。在回归问题中，给定一个训练数据集D，包含K个特征，并行随机森林回归算法的基本步骤如下：

(1)数据预处理后生成RDD数据集。

(2)决策树的构建。从数据集中通过bootstrap采样法生成T组数据集，每组数据集均由抽中数据与袋外数据组成。使用数据集Ti训练生成一棵决策树，在决策树的每个节点进行分裂时，随机从K个特征中选出k个特征，k≤K。在每个节点上，根据最小化平方误差选取最优特征。用spark进行并行不断迭代，最终形成指定数目的相互独立的回归决策树。

(3)建立回归模型。将所有决策树预测值的平均值作为最终输出的预测结果。

随机森林算法属于集成学习算法，由于其样本与特征选择中的随机性，使得随机森林不容易出现过拟合[21]的情况。此外它能够处理高维度的数据，并且不用做特征选择，既能处理离散型数据，也能处理连续型数据，数据集无须规范化。随机森林算法的实际应用将会在第五部分中体现。

4 梯度提升决策树算法原理

梯度提升决策树算法是一种使用决策树作为弱学习器的Gradient Boosting[22]算法。Gradient Boosting方法是boosting方法中的一种，其主要思想是每个新模型的建立是为了使得之前模型的残差往梯度方向减小。GBDT回归算法通过训练多个CART回归树得出基于每个样本的残差，再基于所有的残差训练回归树并且根据回归树的权重更新得出新的模型，即所有回归树的结论累加起来获得最终预测结果[23]。和随机森林算法不同，GBDT 算法的弱学习器之间存在很强的依赖关系。它的损失函数沿着负梯度方向进行迭代[24]，使得损失函数越来越小，模型的偏差也逐渐减小。GBDT的算法步骤[25]如下：

输入：训练集D={(x1,y1),(x2,y2),……,(xM,yM)}；

损失函数L(y,f(x))；

(1)

步骤2：对于t=1,2,……,T：

(1)对i=1,2,……,M，计算损失函数的负梯度在当前模型的值：

(2)

(2)拟合一棵回归树，得到第t棵树的叶节点区域：Rtj，j=1,2,……,J；

(3)对j=1,2,……,J，计算

(3)

(4)更新回归树：

(4)

步骤3：输出最终的回归树：

(5)

5 实验与分析

第五章主要结合实际设计实验，对上文提到的算法进行检验。实验采用大数据平台采集到的某电厂一年的运行数据，对火电厂的供电煤耗进行分析和预测。实验目的在于比较基于spark平台的并行随机森林与GBDT算法在处理回归问题时，模型参数调整上的区别以及调参之后模型的预测效果。

5.1 数据采集和描述

大数据平台采集某电厂2016年9月1日至2017年8月31日周期为一年的运行数据，步长为1分钟。经过业务分析，对数据进行清洗及预处理，剔除异常数据、填补空值后，最终我们提取了7000条工况稳定下的健康数据作为样本数据集。根据灰色关联度分析，选取关联度最大的前12个特征进行分析，其中包括主汽温度、主汽压力、飞灰可燃物等。具体信息见表1：

表1 灰色关联度分析Tab.1 Grey Relational Analysis

续表1

5.2 模型建立

本文主要使用随机森林算法以及GBDT算法对提取的样本数据集(7000条)进行回归建模分析，预测火电厂的供电煤耗，并比较两种模型的预测效果。选择决定系数(R2)[26]、平均绝对误差(MAE)和均方根误差(RMSE)[27]作为评估回归模型预测精度的统计量，具体计算公式分别为：

(6)

(7)

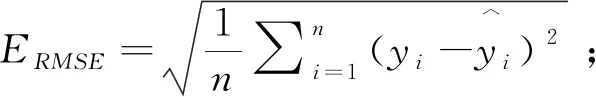
(8)

R2越接近1，说明模型拟合度越高；MAE和RMSE的值越小，说明模型偏差越小，模型精度越高，预测效果更好。

5.2.1 随机森林回归模型

建立随机森林回归模型，首先初始化参数，包括决策树数量、最大深度以及最大分裂数，通过不断调整以上参数的值，使得模型精度达到最高。其余参数均保持一致(分类策略=all，不纯度=variance)，首先调整决策树数量。由于随机森林算法产生近乎独立的预测且最终结果是取平均值，因此增加更多得决策树也不容易出现过拟合的情况。所以我们设置的决策树数量可以尽可能大。保持最大深度(10)、最大分裂数(32)不变，改变决策树数量。决策树数量与平均绝对误差(MAE)以及均方根误差(RMSE)的关系走势图如下(图1)：

图1 不同决策树数量的MAE和RMSE走势图Fig.1 Trend chart of MAE and RMSE with different number of decision trees

从图中可知，当决策树数量较小时，随机森林回归误差比较大。随着数量的增加，MAE和RMSE的值均呈下降趋势，在决策树数目设为350时达到最小值，随后MAE和RMSE的值又会随着决策树数目的增加而逐渐增大。

此外，决策树的深度以及最大分裂数也是两个比较重要的参数。深度增加则训练时长增加，精度也随之提高，但是也更容易出现过拟合的情况，但在随机森林算法中适当增加深度是可以接受的。最大分裂数是指离散化连续特征的最大箱子数，最大分裂数增加，算法的复杂程度和所需的时长也会增加。保持决策树数量(350)不变，通过调整最大深度以及最大分裂数来观察均方根误差随深度的变化。表2显示了不同最大分裂数和最大深度下RMSE值的情况：

表2 不同最大深度和最大分裂数的RMSE值比较Tab.2 Comparison of RMSE of different maximum depth and maximum bins

通过横向比较表中数据可知，随着最大深度的增加，均方根误差在逐渐减小，最大深度为30时均方根误差最小。当最大深度确定时RMSE的值在最大分裂数设为50时最小，随后随着最大分裂数的增加而增加。

综合以上分析，最终将参数设置为：决策树数量=350，最大深度=30，最大分裂数=50，分裂策略=all，不纯度= variance，此时模型的均方根误差为1.211546，拟合优度R2约为0.9919。用剩余20%的数据集作为预测数据集来检验模型的预测效果，预测模型的MAE和RMSE分别为1.341711和3.297954，R2的值为0.940364。从实验结果来看，随机森林回归模型无论在训练和预测时都有较好的表现。

5.2.2 GBDT回归模型

使用GBDT算法建立模型时，同样首先初始化参数，参数不纯度=variance，损失函数=squared，最大分裂数=32均保持不变，通过调整最大深度，学习率(又称步长)以及迭代次数[28]来使得模型达到最优。

学习率以及迭代次数分别设置为0.1、50，改变最大深度(取值分别为5、7、10、12)，平均绝对误差(MAE)以及均方根误差(RMSE)变化趋势如图2所示：

图2 不同最大深度的MAE和RMSE走势图Fig.2 Trend chart of MAE and RMSE with different maximum depth

随着最大深度增加，MAE和RMSE的值不断减小，当最大深度设置为10时，模型的误差就已经很小了，在深度为12时达到最小。接下来将最大深度的值固定(=12)对迭代次数和学习率进行调整。迭代次数也就是弱学习器的个数，学习率又称步长，即每个弱学习器权重的缩减系数，在调参过程中通常用步长和迭代次数一起决定模型的拟合效果。模型的评估结果见表3：

表3 迭代次数和学习率的MAE值以及RMSE值比较Tab.3 Comparison of MAE and RMSE of iterations and learning rate

表3中的结果显示，迭代次数不变，学习率上升，MAE和RMSE的值减小；学习率相同的条件下，若增加迭代次数，也会使得误差逐渐减小，由于迭代次数为100时训练时长较长且为了避免出现过拟合的情况，因此将模型参数最终设定为最大深度=12。由于建模过程中使用的子采样率默认为1，即每次预测时都采用全部数据进行拟合，会导致模型的泛化能力弱。通过调整子采样率以及叶子节点最小样本数则可以防止过拟合问题。保持其余参数不变，将样本子采样率分别设置为0.6、0.7、0.8、0.9，各模型的评估结果如表4所示：

表4 不同子采样率下模型MAE值和RMSE值比较Tab.4 Comparison of MAE and RMSE of different subsample rates

由表中数据可知，当子采样率升高，MAE与RMSE的值会随之减小，当子采样率为0.9时达到最小值。子采样率=0.9保持不变，再将参数叶子节点最小样本数分别设置为5、10、15、20，其余参数一致。各模型均方根误差RMSE和平均绝对误差MAE的走势图如下(图3)：

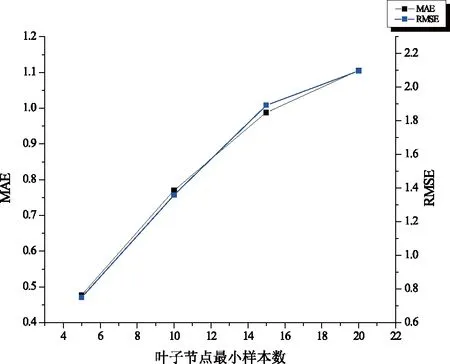
图3 不同叶子节点最小样本数的MAE和RMSE走势图Fig.3 Trend chart of MAE and RMSE with different min_samples_leaf

从图中可知，MAE与RMSE的值随着叶子节点上的最小样本数增大而增大，当此参数设定为5时误差值最小。GBDT模型最终的参数设置为叶子节点最小样本数=5，样本子采样率=0.9，最大深度=12，学习率=0.1，迭代次数=50。使用和5.2.1中同样的测试数据集进行供电煤耗的回归预测，预测评估结果显示预测的均方根误差以及平均绝对误差分别为3.8774、1.7353，拟合优度为0.9176。经过参数调优之后的GBDT回归模型在对火电厂供电煤耗预测中同样有良好的表现。

5.3 实验结果比较和分析

通过以上参数的调优，我们得到了训练好的随机森林回归模型以及GBDT回归模型。用剩余20%的数据对供电煤耗进行预测，模型预测的评估结果如表5所示。表5展示了随机森林算法和GBDT算法在同一场景下最优模型的训练和预测评估结果，综合上文和表中内容，可以得出以下结论：

(1)随机森林参数相比GBDT算法的参数设置更简单，调参的时间更短。

(2)调参过程中，对于同样的数据集，随机森林算法需要把最大深度调到20或以上，而GBDT算法只需调到10，模型就已经有了很高的精度。这也验证了上文提到的两种算法的区别：随机森林算法关注的是降低方差，所以会采用深度很深的决策树；而GBDT是一个逐步消除偏差的过程，对每个基分类器来说它会选择更简单的分类器，所以决策树深度相比而言更浅。

(3)从模型评估结果来看，随机森林无论是拟合还是预测时都有较小的误差和较高的拟合优度。其原因可能是随机森林算法每一轮的训练集都采用有放回随机抽样，而GBDT每一轮会对失败样例赋予较大权重，这就使得GBDT在训练时精度会高于随机森林回归模型。当模型进行测试时，数据集变化，可能会导致GBDT回归模型在预测时的效果并没有随机森林回归模型理想。

(4)对于同一数据集，GBDT回归模型所需的时长远小于比随机森林所需时长。

表5 随机森林和GBDT训练及预测模型评估结果比较Tab.5 Comparison of evaluation results of random forest and GBDT training and prediction models

6 结论

论文详细介绍了基于spark的随机森林算法以及GBDT算法，主要对比了两种算法的原理、参数以及同一场景下的模型效果。最后对实际数据进行建模分析，并对随机森林算法和GBDT算法在回归问题中的表现进行了比较，总的来说，随机森林模型和GBDT模型在火电厂供电煤耗预测中都有较好的表现，但是随机森林模型的预测效果略优于GBDT模型。此外，从参数调优等方面分析，还能得出以下几点结论：(1)随机森林算法和GBDT算法都是基于决策树的集成学习算法，而回归问题中，前者采用取均值得到最终结果，后者采用累加法；(2)随机森林算法采用较深的决策树，而GBDT选择深度较浅的决策树；(3)随机森林算法基于bagging方法，训练的每棵树都相互独立，因而易于并行，而GBDT算法基于boosting方法，每棵决策树之间的依赖程度较大，这就决定了GBDT算法并行起来难度更高。而XGBoost算法解决了这一问题，它可以自动利用CPU的多线程进行并行，在计算速度和准确率上有明显的提升[29]。我们可以在此基础上对XGBoost算法进行进一步的研究，并将此算法运用到人工智能平台中。