采场覆岩光纤监测数据LSSVM填补方法

冀汶莉，郗刘涛，柴 敬

(1.西安科技大学 通信与信息工程学院，陕西 西安 710054；2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室，陕西 西安 710054；3.西安科技大学 能源学院，陕西 西安 710054)

0 引 言

中国工程院主持研究的《我国煤炭资源高效回收及节能战略研究》中指出煤炭目前仍然是中国的重要能源[1]。随着煤炭资源的深度开采，采场上覆岩层出现大空间、大变形的特点[2-5]。与冲击地压的产生有直接关系的采场上覆岩层的复杂变形和运动过程仍难以有效监测、准确表征和精确预测。分布式光纤传感器技术结合数据挖掘技术为解决上述问题提供了可行思路[6-7]。无论是采动覆岩分布式光纤实际监测应用，还是以研究煤岩动力灾害的发生规律以及灾害前兆信息识别为目标的分布式光纤监测的实验室大尺度物理模拟实验，由于光纤传感器的物理特性以及周围地质环境的影响使数据缺失的情况客观存在，这将会导致基于监测数据的学习算法学习到的参数出现偏差，标准差增大，泛化能力减弱等问题[8-11]，最终将影响煤矿灾害前兆信息的精准辨识和预警效果。

目前对于缺失数据处理常用的方法有2类，一是传统方法，如删除法、均值法、以及插值法来填补少数离散缺失值[12]。删除方法在遇到连续缺失或者数据变化幅度较大的情况，不但会丢失一些重要的信息，而且导致数据集规模可能减小。LITTLE和RUBIN详细描述了直接剔除缺失记录可能会导致的严重风险[13-14]。均值在填补小于5%的缺失数据时是一种较为有效的方法[15]。插值法是一种在工程应用中较为常用的插补方法[16]。二是以BP神经网络为代表的机器学习方法或组合方法，如极大似然估计(EM)结合聚类方法[17-18]、朴素贝叶斯[19]、决策树方法进行缺失数据填补[20-21]。极大似然估计是在假设缺失属性和非缺失属性之间存在依赖关系，通过这个依赖关系对缺失数据进行迭代估计，算法的收敛速度慢且效率低。聚类方法是通过测量多属性特征值之间的距离来确定相似性，通过最相似的数据属性值来填补缺失数据，在缺失数据比例较高时，填充的精确度会快速降低。上述方法为解决多属性数据缺失的填补提供了思路，但不适合文中所面对的多测点单属性小样本的缺失数据填补问题。

为解决多测点单属性小样本缺失数据的填补问题，文中以分布式光纤监测系统所获得的不同监测点光纤频率值为研究对象，建立了最小二乘支持向量LSSVM缺失数据填补模型。并将LSSVM与BP神经网络、3次样条插值方法进行对比试验，结果表明3次样条插值和BP神经网络的填补结果鲁棒性和泛化性差，LSSVM插补模型更适合多测点单属性小样本中缺失值的插补。

1 数据样本与缺失特征分析

1.1 数据来源

煤矿开采的上覆岩层变形过程的大尺度物理模拟实验如图1所示，几何相似比为1∶200，模型尺寸为2 000 mm×200 mm×980 mm，从右侧200 mm处向左侧开挖煤层。在模型中布置垂直传感光纤(Fv11，Fv12)，以及百分表。以分布式光纤传感系统监测的Fv11，Fv12上的频率变化来研究上覆岩层的变形发展过程。在监测过程中，由于实验环境和实验材料的物理特性以及周围地质环境的影响，导致采集的Fv11，Fv12上光纤频率数据具有数据缺失现象，实验数据片段见表1,表2。

表1 分布式光纤实验数据展示

表2 分布式光纤实验数据展示

1.2 分布式光纤监测数据缺失特征

1997年RUBIN和LITTEL提出了目前公认的数据缺失分类，根据随机缺失程度分为3类[13]：完全随机缺失(missing completely at random，MCAR)、随机缺失(missing at random，MAR)和非随机缺失(not missing at random，NMAR)。完全随机缺失是指数据缺失的产生是完全随机，不依赖于其他任何变量。随机缺失是依赖于某种因素，不是完全随机缺失，这也是一种最为常见的数据缺失情况。非随机缺失与变量自身或一些不可抗、或未观察到的值相关。

从表1和表2可以看出，分布式光纤监测数据中的缺失数据类型属于MCAR，MAR类以及NMAR类。其中NMAR类的缺失数据，表现为大范围连续0值，可能的原因是光纤拉伸应变超过了自身的测量量程[22-23]。文中着眼研究MCAR，MAR类以及NMAR类连续缺失数据少于5个的填补方法。如果是大于10个以上连续0值的NMAR类数据缺失填补，是缺失数据填补领域的难题之一，拟利用深度学习相关算法从实验反演或趋势预测的角度探索解决方法，因此文中方法不考虑此类缺失数据的填补问题。

图1 物理实验模型及分布式光纤监测布设Fig.1 Physical experimental model and lay outing distributed optical fiber monitoring

为便于分析，文中用D表示分布式光纤实验监测数据全集，描述方法如下式(1)所示。

D={C1,C2,C3,…,Cn}

(1)

式中C1为描述不同光纤传感器位置信息;C2为描述传感器的初始中心频率;C3到Cn为描述实验过程中模拟煤矿开采，开挖到一定位置所有光纤传感器当前时刻采集的光纤频率值；C1和C2数据是已知的，文中重点讨论C3到Cn任意一列缺失数据的填补算法，需要注意C3～Cn是相互独立的，其中Ci可以认为是长时间序列多测点单属性局部小样本监测数据。

定义1：数据缺失模式的定义如公式(2)所示。

(2)

如果Vj(Ci)等于0表示当前位置loca(i,j)监测值是缺失状态。当采用机器学习算法时，以Ci列中没有缺失的数据来推测该列缺失数据的值。

2 基于最小二乘支持向量机(LS-SVM)数据填补模型

2.1 监测数据的空间相关性分析

在物理模拟实验过程中每一次开采会得到一组监测数据即Ci(3≤i≤n)，这些监测数据是进行异常数据识别、覆岩变形趋势预测等研究工作的数据基础。数据缺失会极大降低数据分析的准确性和精度，也会影响规律的正确发现和变形趋势的预测。在图2(a)，2(b)中分别描述了Fv11光纤第一个测点6.940到最后一个测点8.234共127个测点，在开挖到36 cm、54 cm处采集到的光纤频率数据和位置的关系。从图中可看出监测值和监测位置之间有某种非线性关系，其原因是由于不同岩层的岩性、弹性模量以及厚度有所不同，导致监测点的光纤中心频率在煤层开采过程中发生不同程度的偏移。Fv12光纤监测数据也有同样的表现形式。SVM是有数学证明基础的较新小样本非线性回归和分类的机器学习方法[24]，LSSVM是SVM的扩展，在保持较高非线性拟合度的基础上降低了算法的计算复杂度[25]。通过对监测数据的空间相关性分析可知，样本数据具有小样本、非线性的特征，文中提出LSSVM的多测点单属性缺失数据插补方法。

图2 Fv11开采多点光纤传感器采集数据趋势Fig.2 Graph of the date trend based on simulation experiment about Fv11

2.2 算法基本原理

最小二乘支持向量机是传统支持向量机算法的扩展，它利用最小二乘线性系统代替了传统的支持向量机所采用的二次规划方法，在优化模型的基础上提高了算法的执行速度。

假设训练集为Ci=[ci1,ci2，ci3,…,cim,…,cin]，cim为某一个测点的位置和岩层属性组成的向量。输出为Y=[f1,f2,f3,…,fm,…,fn],fm为cim位置点的光纤频率值。将向量cik通过非线性映射φ(xi)函数映射到一个高维的特征空间，然后在这个特征空间中构造优化的线性回归函数，如公式(3)所示。

(3)

(4)

(5)

上述约束优化问题通过引入拉格朗日函数将其转化为对偶问题来进行求解，如公式(6)所示，αi为拉格朗日乘子。

(6)

然后根据KKT条件对参数分别求偏导，如公式(7)。

(7)

通过联立上述方程求解出a和b，最终得到以下的学习模型，如公式(8)所示。

(8)

式中K(x,xi)为核函数，文中选择高斯核函数，如公式(9)所示。它能够实现非线性映射，适用于文中中输入参数较少的情况下实现高维映射的需求。

(9)

2.3 基于最小二乘支持向量机缺失数据填补算法

首先在实验数据集D={C1,C2,C3,…,Cn}中取不含有缺失数据的Ci列(3≤i≤n)，在其上利用随机函数人为产生见表1具有MCAR类和MAR类、NMAR类(连续5个以下的0值)特征的缺失数据，为了验证该方法的插补效果保留原有的对应监测数据。然后将Ci中正常监测值数据形成的子集作为训练样本S_train，挖空的数据形成的子集作为测试样本S_test。算法具体步骤如下。

1)对数据进行预处理。获取到的监测数据中存在着噪声数据，首先使用小波变换的处理方法将数据集Ci中每个监测点的频率数据中包含的噪声数据滤除，使曲线更平滑。

2)在Ci数据集中随机产生缺失数据。为了能够验证学习模型的有效性，在Ci集上通过随机函数确定需要挖去的数据，形成MCAR类和MAR类、NMAR类特征的缺失数据。

3)将以上2步处理好的Ci划分为S_train和S_test样本。

4)设置σ2，γ参数初始值。根据经验在实验过程中设置γ，σ2这2个参数的初始值分别为10和0.1。参数γ是权衡模型复杂度与误差之间的关系，σ为函数的宽度参数，控制了函数的径向作用范围，对系统的泛化能力具有一定影响。

5)对S_train样本进行LSSVM模型训练，输入为位置信息和覆岩层属性组成的向量，输出为该点的频率值。

6)计算MSE指标。MSE(Mean Squared Error)是平均平方误差，在回归问题中常用的参数指标，用来评估在训练过程中模型的可用性。

7)判断MSE是否不变且最小。如果MSE趋于平稳且达到最小就直接到8)，否则调整γ，σ2参数，返回执行5)。

8)输出LSSVM插补回归模型。输出最优参数(γ，σ2)，将最优参数带入LSSVM模型，构建缺失数据插补的回归模型。

3 实验结果分析

文中仿真实验的数据样本集分别由图1所示的采场覆岩变形大尺度物理模拟实验中，Fv11和Fv12这2根光纤上各127个传感器点，在5次模拟煤矿开采过程中采集不含有缺失数据的监测数据组成的6个样本数据集，数据精度为单浮点型光纤中心频率值(GHz)。为了便于实验分析将这些数据集分别定义为：Fv11-2，Fv11-12，Fv11-23，Fv12-12，Fv12-27，Fv12-33其中2，12，23，27，33分别为第2次，12次，23次，27次，33次模拟工作面开采。

在这些数据集上人为构造不同缺失率下的数据缺失，并保留原有的监测数据进行插补效果验证。为了验证算法的有效性和普适性，算法分别在确定缺失率情况下针对离散缺失值和连续缺失值，以及不同缺失率兼具离散和连续缺失等3种情况进行仿真实验并做了结果分析。采用BP神经网络插补方法、3次样条插值方法作为对比算法。

文中采用均方根误差(root mean squared error，RMSE)、最大的偏离量(maximum deviation error，MDE)作为模型的评估指标。其中均方根误差是回归算法常用的评价指标，这个值越小表示填补的数据越准确。然而当极少的填补值为异常值时可能导致这个均方根误差较大，不能很好的评价算法的性能。为了更好的评估算法的性能，文中引入了最大的偏离量MDE作为另外一个评价指标。RMSE和MDE值越小表示填补越准确，算法性能越好。

(10)

MDE=MAX(|yi-fi|),i=(1,2,…,n)

(11)

式中yi为利用插值方法所得的补插值;fi为实际光纤频率监测值;n为缺失数据个数。在公式(10)中MAX表示插补值与实际值差值绝对值的最大值。

3.1 离散型缺失值插补实验分析

按照20%的缺失比率分别在Fv11和Fv12光纤监测数据形成的6个样本集上，随机产生单点离散型缺失数据，使用LSSVM，BP神经网络、3次样条3种插补方法进行缺失值插补实验，实验结果如图3、图4、图5、图6所示。

图3和图5中绿色曲线分别表示对Fv11和Fv12不同6个数据集的缺失值插补拟合，不同形状的图示点表示不同插补算法计算的插补值。从2个图中可以看出当缺失数据为单点离散型时，3种缺失值的插补方法基本可以较好的完成缺失值的插补。但从图3(a)、图3(b)、图3(c)、图4(a)、4(b)、4(c)可直观看出3次样条插值在某些数据集中端点和末尾处填补偏差较大。图3(c)在横坐标7.7～7.8处，以及图5(c)横坐标12.4～12.5处不连续，反映出相邻的2个监测点在此时受岩石力影响不同，在数值上差别较大出现了跳跃现象，在图中表示为间断或跳跃现象。

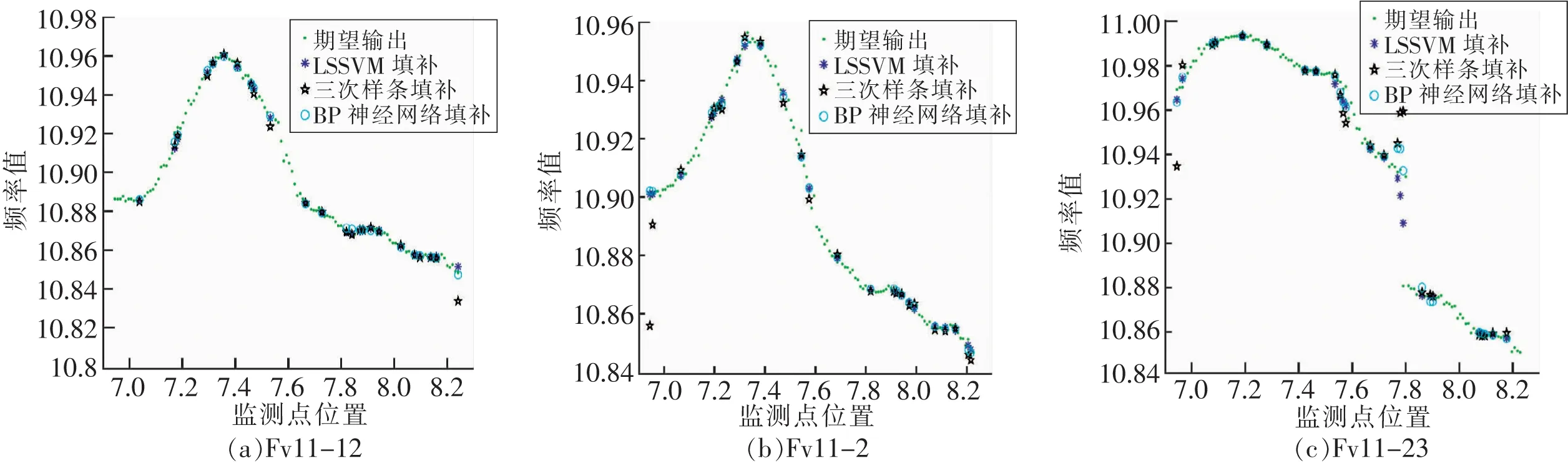
图3 Fv11数据集上单点离散型缺失值插补回归实验结果Fig.3 Results of discrete missing value imputation about Fv11

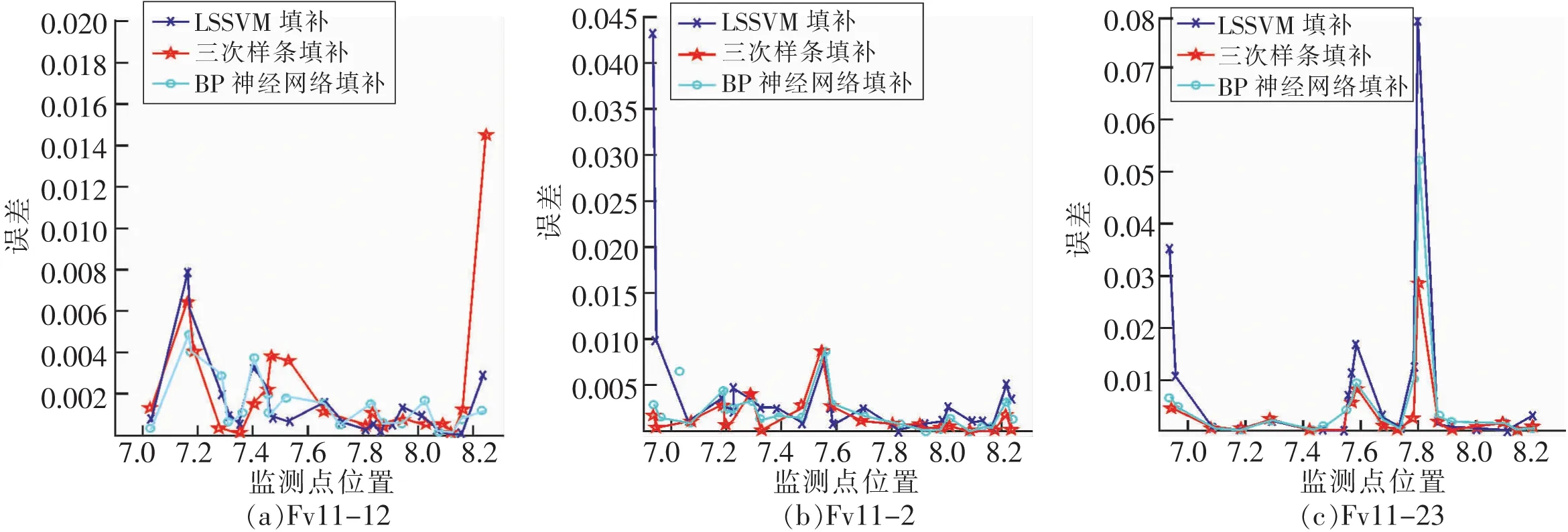
图4 Fv11数据集上离散型缺失值插补回归实验绝对误差Fig.4 Absolute errors of algorithm about discrete missing value imputation about Fv11

在图3(c)、4(c)显示在Fv11-23数据集上横坐标7.8～8附近，以及图5(a)、6(a)显示在Fv12-33数据集上横坐标12～12.2附近，3种插值方法在该位置的绝对误差都比较大，原因是真实监测值在这个位置附近出现了突变，趋势很陡峭。在Fv11和Fv12数据集上直观从图4，图5中可以看出，LSSVM的绝对误差是最小的。

表3描述了Fv11,Fv12上 6个数据集LSSVM，BP神经网络、3次样条插值算法评估指标RMSE和MDE的值。对表3分析可知在Fv11的3个数据集上，LSSVM算法的RMSE，MDE略优于BP神经网络，3次样条插值指标最高，性能相对最差。在Fv12数据集上LSSVM算法的RMSE，MDE略优于3次样条插值，BP神经网络插补方法指标最高。原因是BP神经网络在Fv12波动性较大的数据集上可能会陷入局部最优，导致填补性能指标差。

3.2 连续缺失值插补实验分析

在Fv11和Fv12监测数据中产生的6个样本数据集上进行连续缺失情况的插补实验。按照36%的缺失比例随机在2个数据集上产生连续缺失数据(连续缺失数据个数为3～5个之间)，然后在相应的数据集上使用LSSVN，BP神经网络、3次样条插补方法进行缺失值填补实验。实验结果如图7、图8、图9、图10所示。

图5 Fv12数据集上单点离散型缺失值插补回归实验结果Fig.5 Results of discrete missing value imputation about Fv12

图6 Fv12数据集上离散型缺失值插补回归实验绝对误差Fig.6 Absolute errors of algorithm about discrete missing value imputation about Fv12

图7 Fv11数据集上连续型缺失值插补回归实验结果Fig.7 Results of continuous missing value imputation about Fv11

从图7，图8可知，在Fv11数据集上进行连续缺失值插补时，LSSVM具有较好的拟合趋势。但在图7(a)、图8(a)的横坐标7.3～7.5范围内3次样条连续填补的偏差较大，图7(b)、图8(b)的横坐标7.3～7.5范围内3次样条、BP神经网络的连续填补偏差较大，而且在连续值插补时可能会改变数据的变化趋势。图7(c)、图8(c)的横坐标7.5～7.9范围内3次样条的连续插补偏差较大。从图9、图10可知在Fv12的数据集上进行连续缺失值插补时，LSSVM具有较好的拟合趋势。但在图9(a)、10(a)横坐标12.4～12.6范围内，3次样条和BP神经网络的连续缺失插补偏差较大，而且在连续值插补时可能会改变数据的变化趋势。在图9(b)、10(b)的开始位置3次样条连续填补的偏差较大。

从图8和图10可以看出，当缺失值呈现连续状态，3种缺失值插补算法的绝对误差都在增大。3次样条插值的绝对误差在Fv11数据集上变化幅度较大，在Fv12数据集上BP神经网络变化幅度略高于3次样条，但LSSVM在2个数据集上都有好的拟合表现。

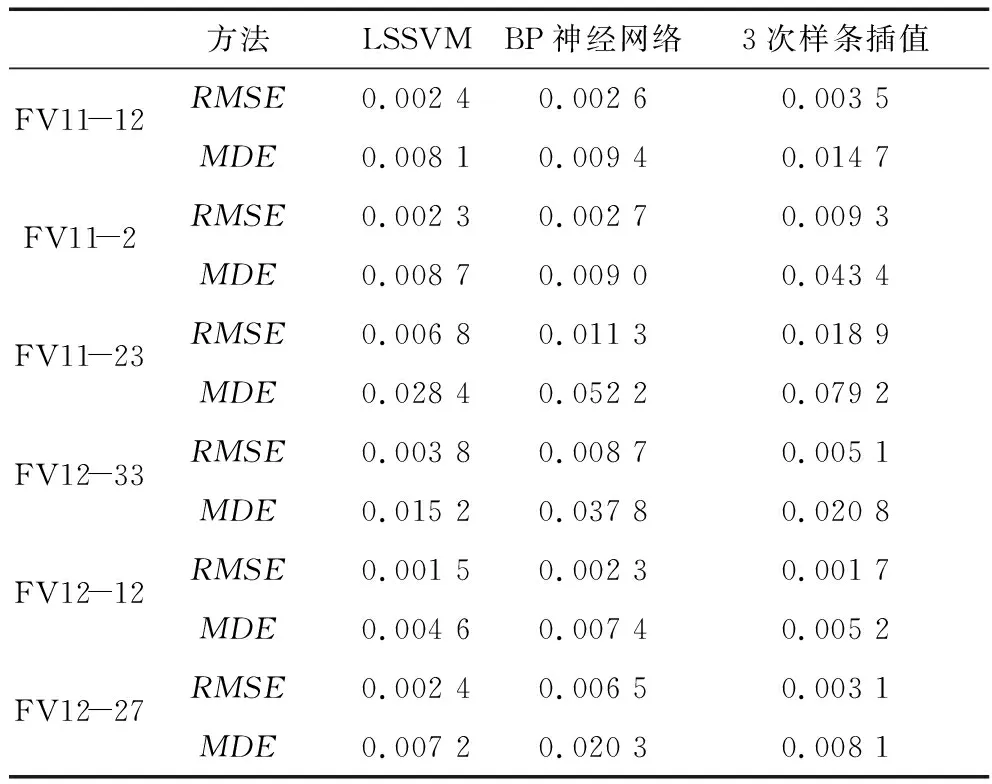
表3 Fv11和Fv12离散缺失值插补方法的RMSE和MDE Table 3 RMSE and MDE based on Discrete missing value about Fv11 and Fv12

图8 Fv11数据集上连型缺失值插补回归实验绝对误差Fig.8 Absolute errors of algorithm about continuous missing value imputation about Fv11

图9 Fv12数据集上连续型缺失值插补回归实验结果Fig.9 Results of continuous missing value imputation about Fv12

表4展示了LSSVM，BP神经网络和3次样条插补算法在Fv11，Fv12数据集上进行连续缺失值插补时评估指标RMSE和MDE值。整体来看连续缺失值插补比离散型插补，3种方法的RMSE，MDE值都有提高。通过对表4分析可知，在Fv11和Fv12不同的数据集上LSSVM均优于BP神经网络和3次样条插补方法。同时可看出在Fv11不同数据集上，由于BP神经网络和3次样条插值均有较大的填补误差，因此这2个方法在Fv11数据集上表现近似。在Fv12-33数据集上BP神经网络插补方法性能在3个算法中最差，原因是由于该数据集非线性波动可能使BP神经网络陷入局部最优。在Fv12-12数据集上由于3次样条插补在起始点处误差最大，导致其RMSE，MDE值较高。在Fv12-27数据集上由于出现了监测值的大跳变导致3种算法的RMSE值和MDE值都变大，但变化平稳。

图10 Fv12数据集上连型缺失值插补回归实验绝对误差Fig.10 Absolute errors of algorithm about continuous missing value imputation about Fv12

表4 Fv11和Fv12数据集上连续缺失值插补方法的RMSE和MDE

3.3 不同缺失比例缺失数据插补实验分析

在实际应用和大尺度物理模拟实验中，较为常见的是监测数据同时具有离散和连续2种缺失形式的情况。为了验证LSSVM算法对于缺失值填补算法的泛化性和适用性，利用随机函数在Fv11，Fv12的6个数据集上同时产生离散和连续2种缺失形态，并在此基础上分别形成不同比例的随机缺失，缺失比例分别为10%，20%，30%，36%，44%，50%。通常情况下无论是物理模拟实验环境还是实际应用环境，缺失数据率低于30%。为了验证算法的极限性能，也为了更准确的分析随着缺失比例的增大，RMSE和MDE值的变化趋势，在30%到50%的缺失比例区间增加了36%和44%的缺失比例。分别采用LSSVM，BP神经网络和3次样条插补算法在Fv11和Fv12对应的数据集上进行所有缺失比例下数据的填补实验。为了保证实验结果的客观性，文中对于每组实验进行50次迭代，表7和表8显示了不同数据集上不同缺失比例下评估指标RMSE和MDE值。

表7和表8显示，在Fv11-12和Fv11-2数据集上当缺失比例为20%及以下时，3种插值方法的RMSE都相差不大，但LSSVM的MDE指标明显优于3次样条、BP神经网络2种方法。随着缺失比例逐渐增大，3种插值方法的RMSE值和MDE值较之前有着明显的上升，但LSSVM的RMSE值均低于3次样条插值法和BP神经网络方法，LSSVM的MDE指标显著低于其他2种方法。对于Fv11-23数据集3次样条的RMSE值和MDE值都是最高的，性能也是最差的。总体上在Fv11数据集不同缺失比例数据插补实验中，LSSVM表现最好，BP神经网络次之，3次样条插值最差。

表5 Fv11，Fv12数据集上不同缺失比例缺失值插补方法的RMSE

表6 Fv11，Fv12数据集上不同缺失比例缺失值插补方法的MDE

在Fv12数据集，随着缺失比例逐渐增大，3种插值方法的RMSE值和MDE值同样有明显的上升，但LSSVM的RMSE和MDE指标值均明显低于3次样条插值法和BP神经网络。当缺失比例低于30%时BP神经网和3次样条插补方法性能基本相似，LSSVM略高于2种方法。当缺失比例从36%升高到50%时，由于3次样条插值方法采用的是数值计算的方式，缺失值填补的准确性快速下降，而基于机器学习的LSSVM方法和BP神经网络显示出了较强的非线性学习能力，因此评估指标均好于3次样条插值，其中LSSVM表现最好。

综合实验分析可知，LSSVM在2根不同光纤产生的6个不同数据集上，不同类型、不同缺失比例下的缺失值插补效果稳定，性能均高于BP神经网络和3次样条插补方法。LSSVM缺失数据插补方法对于长时间序列中多测点单属性局部小样本缺失数据填补是一种有效的填补方法。

4 结 论

1)采场覆岩光纤监测数据呈现了多测点单属性小样本的特性，文中建立了多测点单属性小样本缺失数据LSSVM填补模型。

2)LSSVM填补方法在不同数据集上，针对不同缺失类型的数据插补性能评价指标均高于其他2种方法，预测精度也高于其他2种方法。该方法对单属性小样本缺失数据填补是一种稳定有效的填补方法。

3)3次样条插补方法在端点处可能存在较大的误差，且随着缺失比例提高填补精度下降较快。BP神经网络插补方法随着原始数据的曲线形状不同，在缺失值插补时可能会出现局部最优或改变数据趋势的情况。