基于多装船机的散货船智能装载
方晟,陈顺怀
(武汉理工大学 交通学院,武汉 430063)
货物装载作为货物运输的重要环节,装载效果直接影响着船舶的装载效率、安全性能,以及航行性能。现有的船舶装载方案主要由大副基于工作经验来制定并对其进行校核计算来得到,该种方式仅仅考虑了装载方案的可行性,并未考虑方案的优化。此前关于散货船智能装载问题的研究大多未能将货物分舱和装货过程综合考虑,且没有考虑到多装船机进行装载的情况[1-7]。而在现实中,随着散货船的吨位越来越大,存在着使用多装船机同时进行装载作业以提高装载效率的情况。为此,提出相应的数学模型,综合考虑装船机数量、装载轮次、装载顺序、货物种类和装载量的影响,使用改进多目标遗传算法进行求解;最后,通过实例计算对该算法的求解性能进行验证。
1 智能装载问题的数学模型
1.1 问题描述
散货船智能装载问题是一个多目标、多约束的NP问题。散货船在制定装载计划时,需要综合考虑装船机数量、装载轮次、装载顺序、货物种类和装载量的影响。为保证船舶安全,装载通常分多轮、多步进行。当所有的装船机均完成当前货舱的装载任务且相应压载水舱中的压载水全部排完时,即为一步。如图1所示,n为散货船的货舱数目,m为装船机的数目,且n>m≥1。由于所有的装船机在同一轨道上进行移动,故各台装船机不能够相互跨越。在一步装载过程中,只有当全部装船机全部完成装载作业后,装船机才可进行移动。
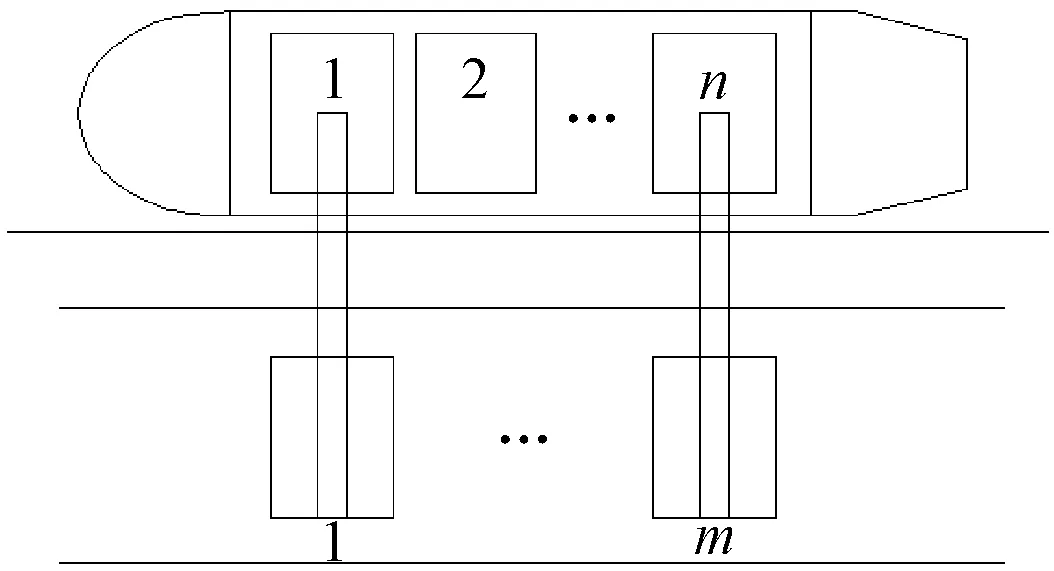
图1 多装船机装载示意
定义以下3个优化目标:①减少船舶装载作业时间,提高船舶的装载效率;②减小船舶实际艏艉吃水差与最佳艏艉吃水差(设计纵倾)的差值,以使船舶具有良好的浮态,从而使其快速性较好;③最小化船舶最大静水弯矩值,以保证其结构强度的安全。
1.2 装载效率的近似计算
装载计划中装载效率的高低是评价装载计划好坏的一个重要因素,提出近似计算散货船装载时间的方法以判断船舶的装载效率。影响船舶装载效率的因素主要包括装船机装载作业时长、压载水排放时长,以及装船机移动时长[8]。
(1)

(2)
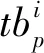
(3)

通常散货船在进行装载作业时,第一次装载某一货舱,同时排空该货舱所对应压载舱中的压载水。故每一步的装载过程中,作业时长是由装船机装载时长与压载水排放时长的最大值来决定的。建立装载效率近似计算公式。
(4)
1.3 优化模型的建立
在船舶装载的过程中,考虑到舱容、稳性、浮态、结构强度等条件的限制,构建散货船智能装载问题的数学模型如下。
minf1=t
(5)
f2=|Δd-Δdopt|
(6)
f3=|Msmax|
(7)
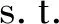
(8)
(9)
df[i]≤dfmax
(10)
da[i]≤damax
(11)
Δdmin≤Δd≤Δdmax
(12)
k[i]≥1
(13)
(14)
Ns[i][j]≤Ns[j]max
(15)
Ms[i][j]≤Ms[j]max
(16)
Wh[i]≤Whmax
(17)
每一种货物的分步装载量之和wji应与该种货物的总计划装载量wj相等;每舱的计划装载货物体积不能超过该舱的舱容大小;在装载过程中船舶的艏吃水不能超过限定值;在装载过程中船舶的艉吃水不能超过限定值,且装载完成后应保证螺旋桨完全浸入水中;船舶装载完成后的艏艉吃水差应保持在一定的范围内,以满足船舶航行性能的要求;装载过程中船舶的稳性衡准应满足要求;装载过程中船舶的初稳性高不能小于规定的最小值;每一步装载后的船舶在各个剖面的静水剪力值不得超过该剖面的许用静水剪力值;每一步装载后的船舶在各个剖面的静水弯矩值不得超过该剖面的许用静水弯矩值;每个货舱所装载的货物重量不能超过该货舱的极限装载重量,以满足船体局部强度的限制。
散货船智能装载问题是一个多目标、多约束的非线性优化问题,无法使用传统的数值解法求取精确解,因此使用智能优化方法来求取优化解。
2 多目标遗传算法求解
2.1 编码方式
在散货船智能装载问题中,共有3类变量,分别是每一舱装载的货物种类、每一步装载的货舱号和每一步的装载重量。其中,货物种类编号和货舱号为离散变量,故用整数来表示;装载重量为连续变量,以实数表示。故采用整数编码与实数编码相结合的级联编码方式对控制变量进行编码,编码格式可表示为
X=[C|H|W]=[c1,c2,…,ci|h1,
h2,…,hk|w1,w2,…,wk]
(18)
式中:i为船舶货舱数目;k为总装载步数;C=[c1,c2,…,ci]表示每一货舱所对应装载的货物种类;H=[h1,h2,…,hk]表示每次装载所对应的货舱号,由于有多台装船机同时进行装载作业,故其应满足一定的约束条件。若有m台装船机进行作业,则1,2,…,m号装船机在第一步装载时对应的货舱号分别为h1,h2,…,hm,且h1 染色体的交叉和变异是遗传算法中更新个体的重要过程。针对染色体变量类型的不同,交叉变异方式也有所不同。 交叉:染色体的变量C和H为整数编码,采用顺序交叉的方法进行交叉操作。在交叉的过程中,应保证满足编码的约束条件,C变量顺序交叉的示例见图2。W变量为实数变量,采用实数交叉运算方式[9]。 图2 整数变量顺序交叉示例 变异:与交叉一样,对整数编码变量C和H使用随机交换变异的方法进行变异操作,对实数变量W使用实数变异运算方式。 步骤1,初始化算法相关参数。 步骤2,产生初始种群。 步骤3,计算种群中各个个体的目标函数值,然后对各个个体进行非支配排序。 步骤4,保留非支配解所对应的个体直接进入下一代。 步骤5,剩余个体进行交叉、变异操作,得到新一代的种群。 步骤6,重复步骤3~5,判断是否达到指定的遗传代数,若达到,则结束算法,输出优化解;否则重复上述过程直至结束。 以上是一种基于Pareto前沿的多目标遗传算法的运行步骤,该算法可以得到多个优化解,决策者可根据自己偏好来选择具体方案。 某20 000 t散货船船长150 m、宽24 m,型深11.8 m,设计吃水为9.1 m,设计纵倾为0 m。该船有4个货舱,19个压载水舱,货舱及压载水舱的分布情况见图3。该船装载轮次为2轮。 图3 某20 000 t散货船货舱及压载水舱分布 装载的货物为单一货种,密度ρ=4.5 t/m3,积载因数kc=1.045 m3/t,装载总重量w=21 650 t,调用2台装船机进行装载作业,2台装船机的装载速度均为3 000 t/h。在使用上述的多目标遗传算法求解时,种群数目为50个,遗传代数为500代,交叉概率为0.9,变异概率为0.05。 该算法通过使用C#编程实现,系统运行环境为:Intel(R) Core(TM) i5-5200U CPU、Windows7操作系统、8GB运行内存,优化计算运行时间约为13 min。对该装载案例经过50次随机计算,其中48次可得到优化解。某次优化计算后得到如图4所示的Pareto前沿。 图4 装载案例的Pareto前沿 选取其中一个优化结果见表1,该优化结果所对应的每步装载过程船舶性能指标参数见表2。 表1 装载案例的优化结果 表2 装载案例每一步装载对应的船舶性能指标 将优化结果与装载手册提供的实际结果相比较,见表3。 表3 优化装载结果与实际装载结果对比 可以看出,优化后的船舶浮态得到较大优化,艏艉吃水差更加靠近设计纵倾值,并且装载作业时间和船舶最大静水弯矩值较装载手册提供的实际装载结果分别下降了7.13%和15.08%。由此可见,该算法具有一定的可行性。 采用的多目标遗传算法能够获得合理的优化解,对船舶的装载效率、浮态和结构强度实现了优化,可为船舶智能装载问题提供参考。2.2 交叉和变异

2.3 算法运行步骤
3 装载案例与结果分析





4 结论

