嵌入式带缆桩甲板加强结构设计
闫小顺,汤刚,骆伟,梅国辉
(中国舰船研究设计中心,武汉 430064)
带缆桩属于船舶系泊系统的重要承载设备,船舶在进行系泊、拖带等操作时,船上系缆索的固定装置主要为带缆桩,承担着系缆索传递的外载荷。随着动力和载重的不断提升,船舶在进行系泊或拖带时,带缆桩所承受的载荷也逐渐增大,带缆桩的船体结构加强对船舶系泊安全至关重要,有学者对带缆桩的选型和船体加强结构强度计算校核等问题进行了研究,提出了几种提高带缆桩承载能力的建议,同时建议在后续研究中结合船体结构的加强进一步分析高负荷带缆桩的设计方法[1];以某舰船尾部甲板带缆桩为研究对象,通过有限元直接计算方法研究带缆桩甲板加强结构[2];通过有限元直接计算对大型散货船带缆桩结构加强进行分析[3-4]。本文对嵌入式带缆桩加强结构进行数值仿真分析,探讨甲板厚度、加强结构尺寸、节点连接形式等对仿真结果的影响,并对连接型式、过渡距离等方案进行对比。
1 加强结构常用形式
按照标准GB/T554—2008,常用的带缆桩主要有普通带缆桩(A型)、嵌入式带缆桩(B型),其结构型式见图1。

图1 国内带缆桩常用型式
A型带缆桩带有一个较大的底座,直接焊接在甲板上;B型带缆桩中一段桩柱嵌入甲板下,与船体甲板及其下方的加强结构连接在一起。A型带缆桩底座较大,占用较大的甲板面积,因此对于布置紧张的船舶更倾向采用B型带缆桩。
嵌入式带缆桩的甲板加强结构一般采用交叉的T型材,T型材一般考虑船体本身结构后纵向或横向布置,典型的带缆桩加强方案见图2。

D-带缆桩直径;t1-甲板厚度;t2-T型材的腹板厚度;h2-T型材的腹板高度;t3-T型材的面板厚度;h3-T型材的面板宽度图2 嵌入式带缆桩典型加强结构型式
2 加强结构尺寸
2.1 结构应力简化计算分析
对于1根缆索以“8”字形缠绕于桩柱上的带缆桩结构,1根绳索对桩柱所产生的力接近于绳索内力的2倍[5]。如果绳索的破断载荷为SWL,那么带缆桩所承受的最大载荷F=2SWL。在力F的作用下,可以将带缆桩简化为悬臂梁,则绳索对甲板及加强结构的最大弯矩为
Mmax=F×h1=2SWL×h1
(1)
带缆桩处的甲板及甲板加强T型材结构将联合抵抗上述弯矩的作用。假定嵌入式带缆桩处甲板及甲板加强T型材组成如图3所示的工字钢结构,则可认为甲板及加强结构的最大应力为

图3 等效工字钢型式及参数
(2)
式中:σmax为加强结构的最大应力;Wmin为单个工字钢的最小剖面模数,γ1为剖面模数放大效应系数(可看作横向和纵向T型材及甲板均对带缆桩的约束与单个工字钢对带缆桩约束的比);γ2为应力集中放大系数。
2.2 加强T型材腹板高度的影响
对图2所示的嵌入式带缆桩及甲板加强结构建立有限元简化计算模型,见图4。

图4 典型带缆桩加强结构简化分析模型
模型选取某船甲板上嵌入式带缆桩周围区域,尺寸为6 m×4 m,带缆桩直径D为400 mm,甲板以上的高度为600 mm,甲板以下的高度为400 mm。甲板厚度t1=10 mm,腹板高度为t2=10 mm,面板宽度h3=100 mm,面板厚度t3=10 mm,带缆桩缆索的破断载荷为314 kN,作用在带缆桩其中一根桩柱上,作用点在甲板以上0.8D处。经计算,当腹板取300 mm时,模型的变形及von Mises应力云图见图5。带缆桩的最大von Mises应力随着T型材腹板高度的变化见图6。
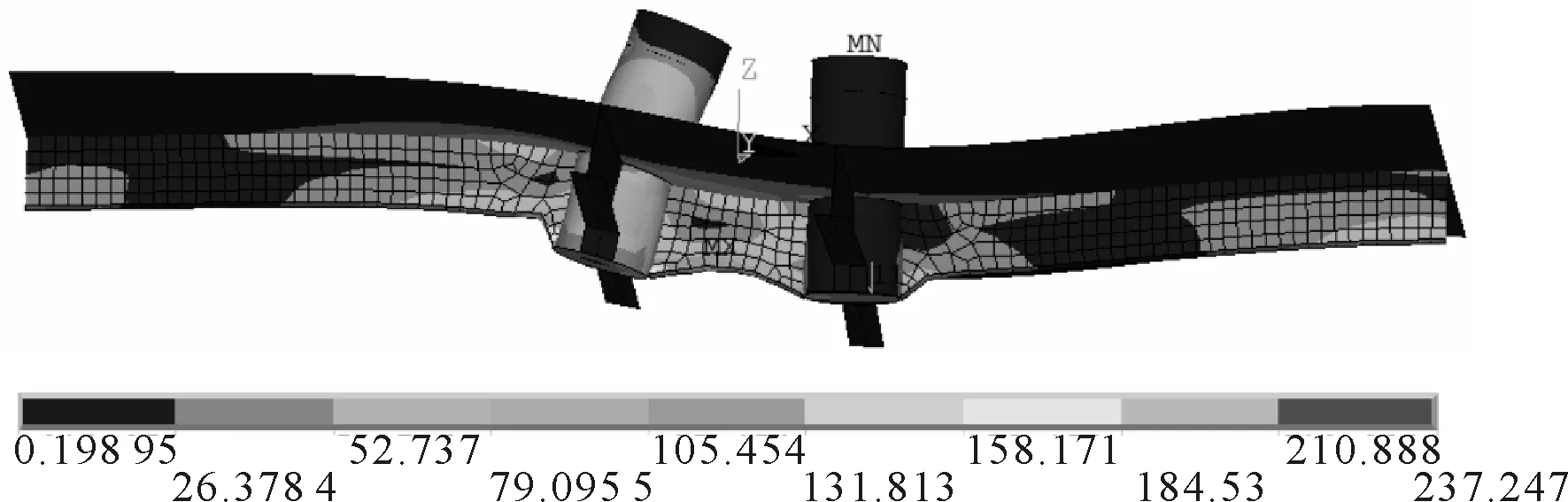
图5 最大von Mises应力云图

图6 最大应力随腹板高度的变化
不难看出,最大应力随着腹板高度的增加而显著降低。这是因为随着腹板高度的增加,等效工字钢的剖面模数显著增加,根据式(2),相应最大应力也会随之减小。此外,γ2/γ1取0.5时,式(2)与有限元数值计算结果较为接近。
2.3 甲板厚度及T型材面板对强度的影响
采用上述嵌入式带缆桩结构,改变甲板厚度t1,模型最大von Mises应力随甲板厚度的变化曲线见图7。改变面板规格t3×h3,则模型最大von Mises应力随面板规格的变化见图8。

图7 最大应力随甲板厚度的变化

图8 最大应力随面板规格的变化
不难看出,最大应力随着甲板厚度的增加而降低,但降幅并不明显;最大应力随着T型材面板规格的加大而降低。这是因为,甲板厚度增加可以增大等效工字钢的剖面模数,但对最小剖面模数的影响有限,而增大面板规格,最小剖面模数增加明显。此外,γ2/γ1取0.5时,式(2)与大部分有限元数值计算结果较为接近。
3 加强结构设计影响因素
3.1 加强T材与带缆桩的连接
T型材结构与固定端的连接主要有两种,一种是腹板双面焊接在固定端,而面板削斜;还有一种是T型材腹板和面板均牢固焊接在固定端上,见图9。
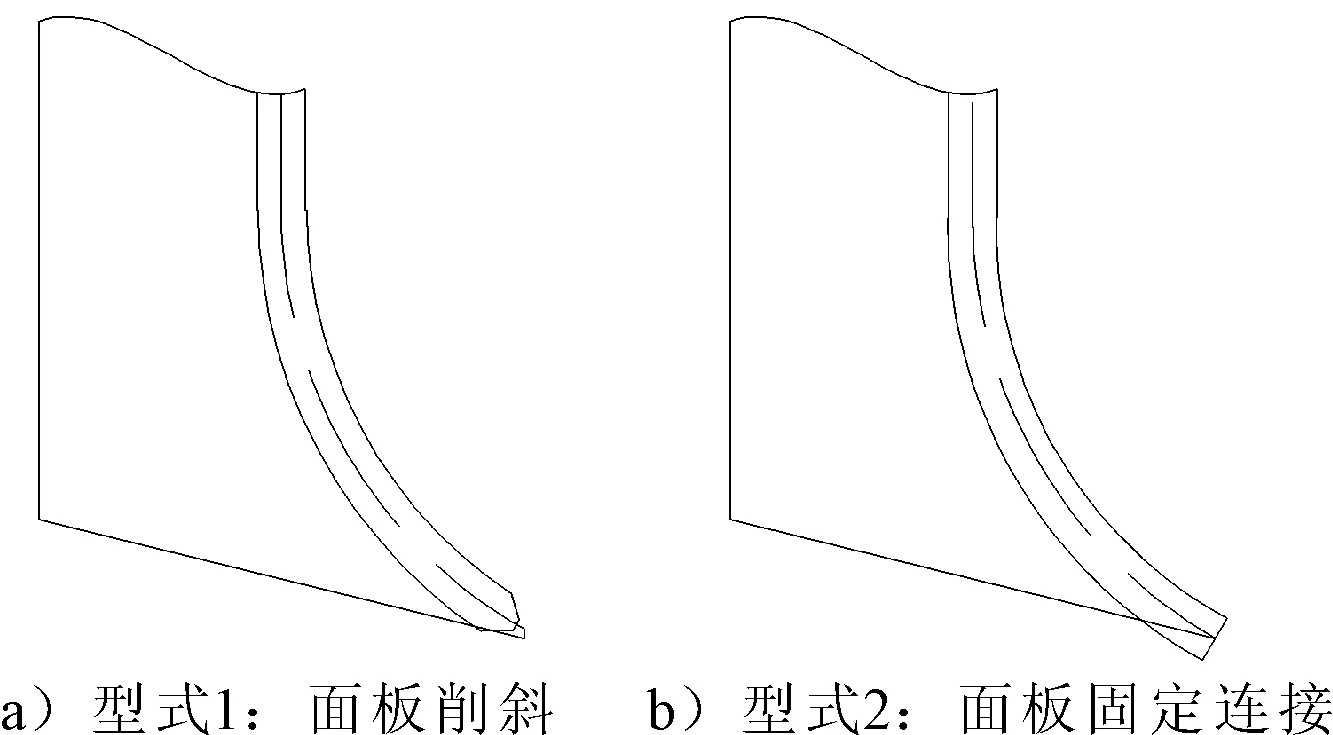
图9 加强T材固定端连接典型型式
为了对比2种连接方式连接对结构强度的影响,建立相应的有限元模型,模型中带缆桩的受力及加强结构与上文保持一致,仅改变T型材与带缆桩的连接型式,计算结果见图10。

图10 最大应力与固定端连接的关系
可以看出,当腹板高度较小时,型式1与型式2差别不大,但当腹板高度接近带缆桩甲板下端高度时,型式1的von Mises应力明显比型式2的要大。这是因为,当腹板较小时,应力最大点出现在腹板由大变小的转折处;而随着腹板高度变大,最大应力出现在面板与带缆桩的连接处,此时当T型材的面板牢靠连接时,可以参与弯曲,从而应力比面板削斜时要小。因此,一般建议面板与带缆桩采用型式2的面板固定连接型式。
3.2 加强T材放大距离
嵌入式带缆桩加强T型材结构一般要考虑甲板横梁和纵桁原有的高度,因此加强T型材都要经过一定距离的过渡。过渡的距离(图2中的b)是设计人员考虑的重要因素之一。建立相应的有限元模型,T型材腹板高度取200 mm,并与带缆桩过渡连接。改变b与a的关系,计算模型的von Mises应力,结果见表1。

表1 不同过渡距离的应力计算结果
不难看出,过渡的距离b越大,最大应力就越小,当b增大到3a以上时,应力减小的越来越慢。这是因为,过渡距离大,应力集中系数就越小,当过渡距离大到一定程度,最大应力就不再发生在两个带缆桩外T型材腹板变小处,而是出现在两个带缆桩间的T型材连接处。结合应力集中系数的变化规律[6],建议过渡距离b不小于5a。
3.3 带缆桩壁厚对结构的影响
在铸造带缆桩桩柱时,桩柱厚度不一定均匀。取T型材面板规格为10×100,腹板规格为10×300,那么有限元模型最大von Mises应力随桩柱厚度的变化规律见图11。
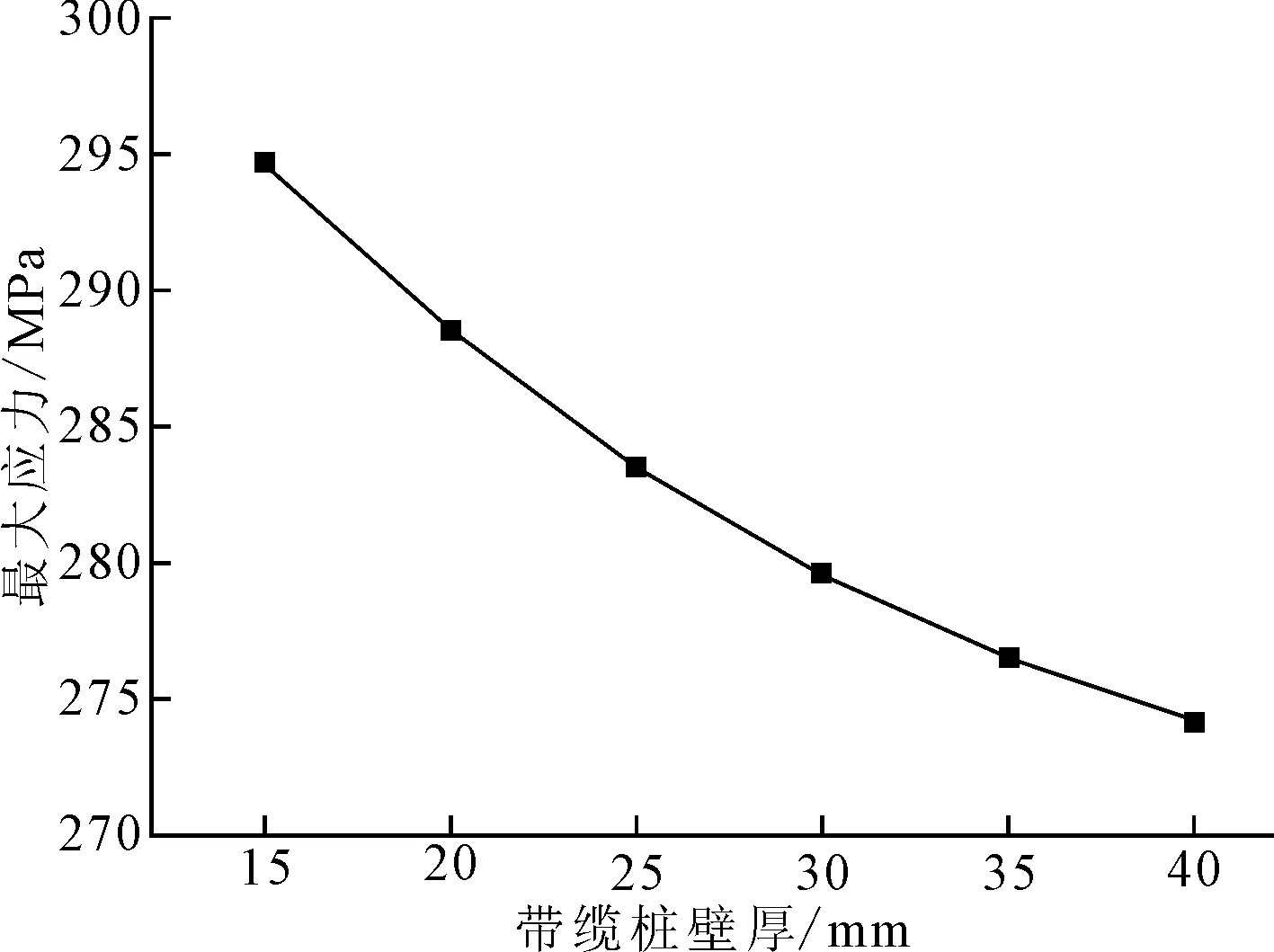
图11 最大应力随带缆桩壁厚的变化
可以看出,带缆桩壁厚越厚,最大应力越小,但变化并不显著。因此,带缆桩壁厚对结构强度有一定影响,但相比于腹板、面板等因素而言,带缆桩壁厚对结构受力影响可以忽略。
4 结论
1)嵌入式带缆桩甲板加强T型材的腹板高度、面板规格对结构强度影响显著,甲板厚度、带缆桩壁厚等对结构强度影响较小。
2)嵌入式带缆桩甲板加强T型材面板与带缆桩牢固连接方案较优;建议T型材腹板过渡距离不小于腹板与带缆桩甲板下高度差的5倍。
3)在初步设计时,可采用文中最大应力估算公式进行加强结构尺寸估算,其中γ2/γ1取0.5;详细设计时,则可采用数值有限元计算方法对嵌入式带缆桩的甲板加强结构进行强度校核,为嵌入式带缆桩甲板加强结构的设计提供依据。

