自适应阈值小波在指纹图像去噪中的应用

林玉娥，孙然然，梁兴柱，2，苏树智

(1.安徽理工大学计算机科学与工程学院，安徽 淮南 232001;2.安徽理工大学环境友好材料与职业健康研究院(芜湖)，安徽 芜湖 241003)

指纹识别是根据识别对象的指纹进行分类比对，从而对识别对象进行判别。近些年来，指纹识别技术逐渐成熟，已经在人类的生产生活领域得到了广泛地应用。快速并且准确地提取指纹的细节特征是指纹自动识别系统的重要环节之一，但是通常获取的指纹图像会受到设备和环境的影响，使得获取的指纹图像含有椒盐和高斯等混合噪声，进而影响指纹识别的识别速度和准确性，所以对指纹图像的噪声去除研究是非常重要的。文献[4]提出一种小波域的贝叶斯算法进行指纹图像的噪声去除；文献[5]提出了让含噪图像邻域或者整个图像全部像素加权均值与其相似版块冗余性结合起来的一种非局部均值滤波去噪算法；文献[6]提出了局部方向场非局部均值(Non local mean of local direction fielcl,NLM-LDF)实现对指纹图像噪声进行去除；文献[7]把深度学习引入方向场校正以实现指纹图像噪声去除。但是这些算法都属于空域算法，对于指纹图像的混合噪声去除工作并不理想。因为在时频域内信号表征良好，小波阈值算法被广泛应用于图像去噪中。传统的小波变换阈值去噪算法主要是软、硬阈值去噪算法。由于软、硬阈值函数存在的偏差和不连续等问题，因此对图像噪声的去除效果并不令人满意。文献[14]提出了一种基于新型符号函数的改进算法，相比于经典的小波去噪算法具有较好的鲁棒性。文献[15]提出的改进阈值函数的小波降噪方法，相比于经典的小波去噪算法效果有较好提升，但是函数不连续的情况并没有改善。文献[16]提出的改进阈值函数算法能有效地去除图像中的高斯噪声。文献[17]提出的改进小波阈值去噪算法，较好地解决了经典阈值函数的不连续和存在偏差的问题。但是以上的去噪算法只能针对单一噪声，不能有效地处理混合噪声。

本文为了有效地去除指纹图像的混合噪声，基于小波阈值算法和中值滤波算法，提出了一种改进的自适应阈值和连续型低误差阈值函数的小波去噪算法。该算法首先对含噪的指纹图像进行一次中值滤波，使得混合噪声里面的椒盐噪声有较好的去除效果。接着设计了一种可以随着分解层数不断变化的自适应阈值，使得估计系数对噪声信号误判的问题得以解决。然后，设计了一种有更好的连续性和低误差阈值函数，让估计系数和真实系数之间更加贴近，从而可以有效地去除图像中的混合噪声。仿真实验表明，本文算法对含有混合了高斯和椒盐噪声的指纹图像有较好的噪声去除效果，图像的指纹细节显示得更清晰，明显优于其他对比算法。

1 图像去噪理论

1.1 中值滤波

中值滤波算法是一种非线性平滑滤波，中值滤波噪声去除的基本原理是用该噪声点邻域各点像素值的中值代替图像的噪声点，去除噪声，得到去噪后的图像。

二维中值滤波公式如下

g

(

i

,

j

)=med{

f

(

i

-

m

,

j

-

n

)},(

m

,

n

∈

W

)

(1)

式中：

f

(

i

,

j

)为原始图像，

g

(

i

,

j

)为去噪后的图像，

m

为窗口水平尺寸，

n

为窗口垂直尺寸，

W

为二维模板。

对含噪声图像进行中值滤波噪声去除后输出的像素点是邻域内真实信号的中值，因此邻域内的极限像素值对于图像去噪并没有很大的影响。根据椒盐噪声本身就是由像素的极大值或极小值构成的噪声，因此图像中含有椒盐噪声时常用中值滤波方法去除。

1.2 小波阈值去噪

小波阈值算法去噪的原理是根据含噪图像进行小波分解后随着分解层数的增大真实信号会逐渐增大、噪声信号会逐渐变小而设置一个合理的阈值，然后进行信号重构得到去噪后的图像。

硬阈值函数的公式如下

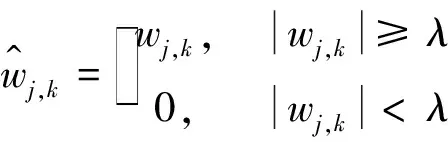
(2)

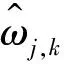
全局阈值的公式如下所示

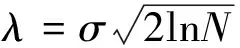
(3)

式中：

σ

是噪声标准方差，

N

是信号的长度。

σ

采用中值估计法得到，计算公式如下

(4)

式中：

Y

(

m

,

n

)是子带系数。

软阈值函数的公式如下

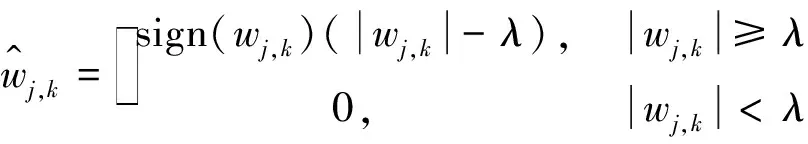
(5)

式中：sign()是符号函数。

软、硬阈值去噪算法函数图像如图1所示

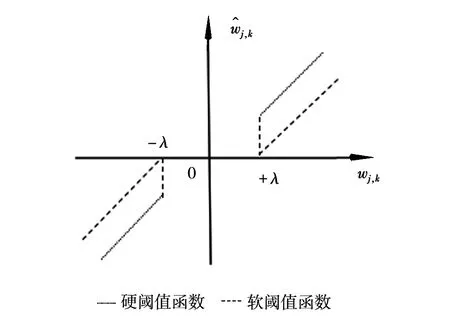
图1 硬、软阈值函数图像

由上面的函数图像得知，硬阈值函数图像在阈值±λ处不连续，所以在去噪过程中会产生图像失真现象。尽管软阈值函数在±

λ

是连续的，但它和真实信号之间的偏差总是存在，去噪后图像会出现边缘模糊。因此软、硬阈值去噪算法虽然在图像噪声去除过程有效果但是仍存在问题。

2 改进的自适应阈值算法

2.1 改进的自适应阈值

传统的软、硬阈值去噪算法无论在哪一层使用阈值都是全局阈值

λ

，小波分解噪声图像时，实际情况是分解层数越大，噪声系数值就会越小。因此使用统一阈值进行估计小波系数会造成对噪声信号错误判断，把真实信号当作噪声信号去除，所以噪声去除后图像的质量就会受到影响。为了取得的阈值更符合实际，提出了一种可以根据分解层数不断变化的新阈值

(6)

式中：

i

为分解层数，

T

为第

i

层的阈值。新的阈值

T

会随着分解层数增加自适应调整为较小的阈值，更加符合真实情况下分解层数越高噪声信号的模值越小这一事实，新阈值可以更好解决传统全局阈值

λ

出现的噪声信号错误判断问题，实现了对噪声系数更准确识别。

2.2 连续型低误差阈值函数

为了使经典阈值函数存在的误差和不连续得以解决，提出了一种连续型低误差阈值函数，连续型低误差阈值函数的含义如下。

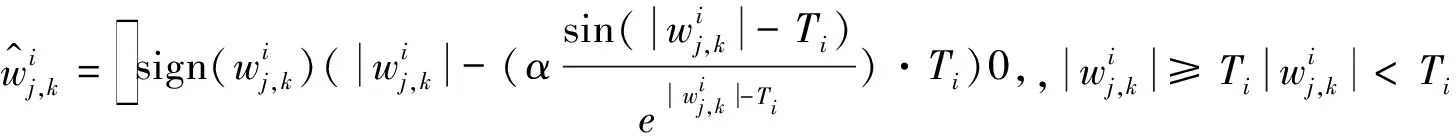
(7)

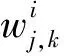
连续型低误差阈值函数的图像如下

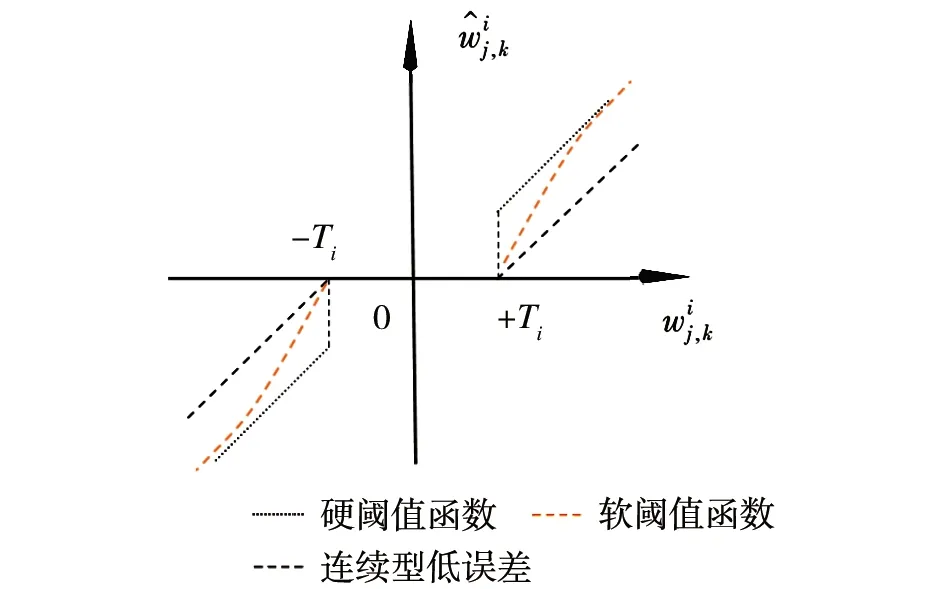
图2 连续型低误差阈值函数图像

下面对连续型低误差阈值函数进行分析

1)连续型低误差阈值函数的连续性

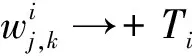
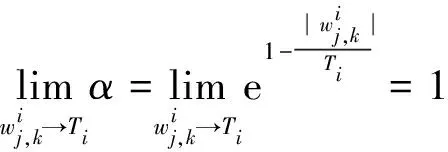
故：

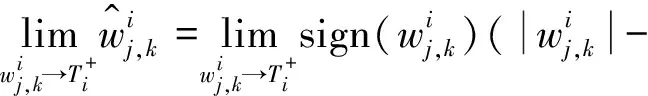
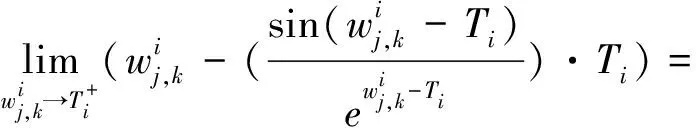
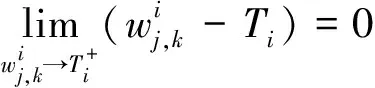
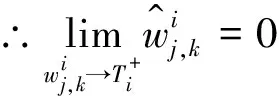
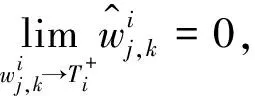
同理

综上所述，连续型低误差阈值函数在±

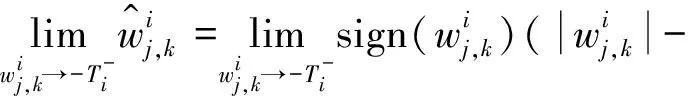
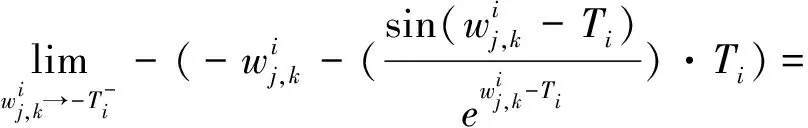
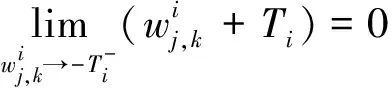
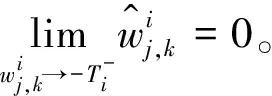
T

处都是连续的，所以连续型低误差阈值函数相比于硬阈值函数避免信号震荡。

2)连续型低误差阈值函数的渐进线

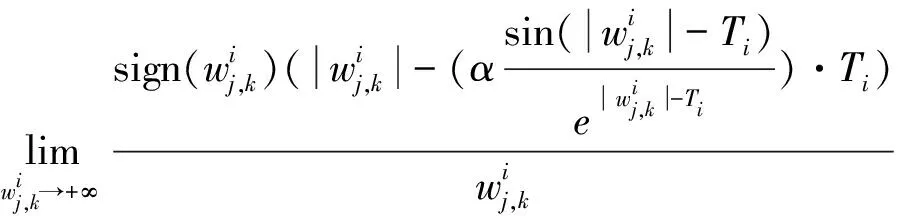
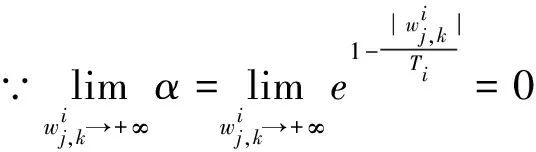
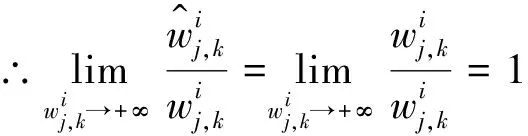
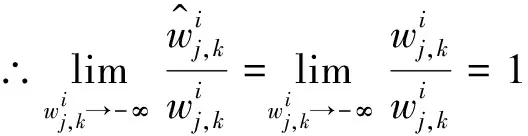
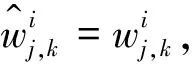
3)连续型低误差阈值函数的偏差性

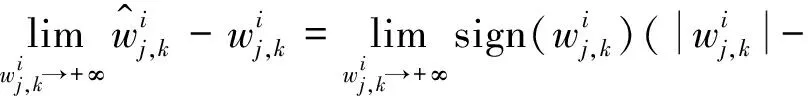
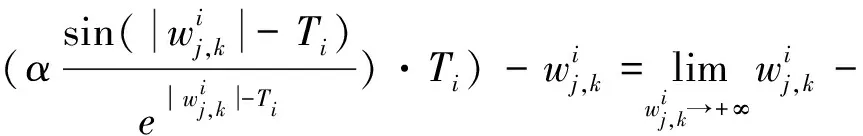
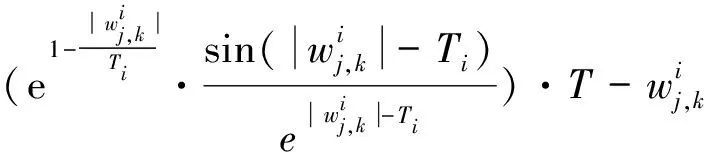
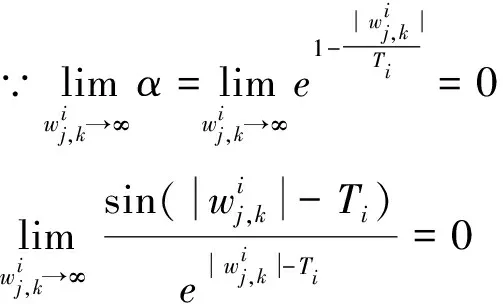
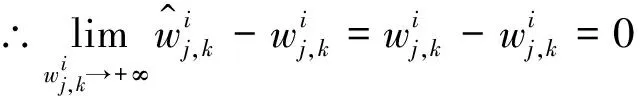
同理

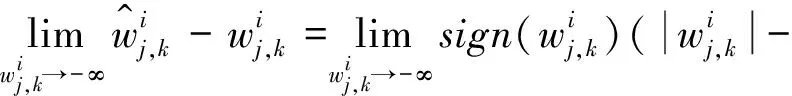
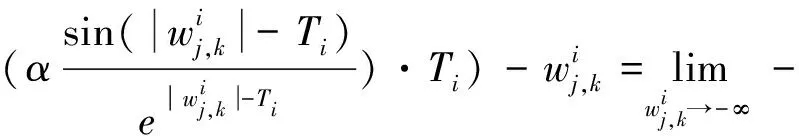
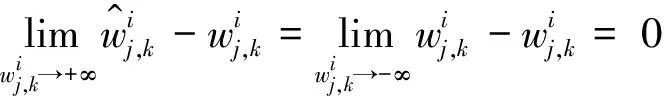
因此，对连续型低误差阈值函数从数学角度分析之后发现，连续型低误差阈值函数在阈值处是连续的， 使得硬阈值函数的不连续得以解决，而且随之小波系数增大，取得的估计阈值与真实阈值之间的偏差也会越来越小，并且在无限大时趋近于0。

2.3 算法实现步骤

为了更好去除混合噪声中的椒盐噪声，先用中值滤波进行去噪，然后使用自适应阈值

T

和连续型低误差阈值函数的小波算法进行进一步的去噪处理。算法的步骤归纳如下1)输入原始图像

f

(

i

,

j

)；

2)给原始图像添加噪声；

3)对含噪图像进行中值滤波去噪；

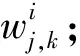
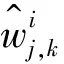
6)小波系数重构；

7)输出去噪后的图像

g

(

i

,

j

)。

3 仿真实验

为了验证算法的有效性，在Win10系统中，Matlab R2016a环境下进行本文算法的实验。考虑到指纹图像的特殊性选用三幅大小适宜、指纹纹路清晰的指纹图像作为测试图像，三幅测试图像选自FCV2004指纹数据库中101_2.tif、107_3.tif、109_5.tif 三幅指纹图像。对实验的三幅指纹测试图像进行编程，将实验结果分别对比于传统的硬阈值、软阈值、半软阈值、改进曲波变换和NLM-LDF。本文实验中，对测试的三幅指纹图像进行3层小波分解，小波基函数选用sym8。三幅测试图像的原图如图3所示。

图3 测试图像原图

不同算法对含高斯噪声的方差是0.01，椒盐噪声的密度是0.01的混合噪声101_2.tif指纹图像进行噪声去除，去噪后图像如图4所示。

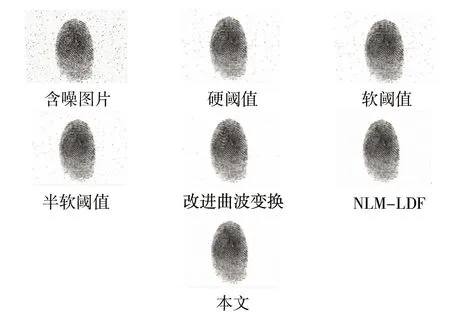
图4 不同算法对含混合噪声的101_2.tif图像的去除效果

不同算法对含高斯噪声的方差是0.01，椒盐噪声的密度是0.01的混合噪声107_3.tif指纹图像进行噪声去除，去噪后图像如图5所示。

不同算法对含高斯噪声的方差是0.01，椒盐噪声的密度是0.01的混合噪声109_5.tif指纹图像进行噪声去除，去噪后图像如图6所示。

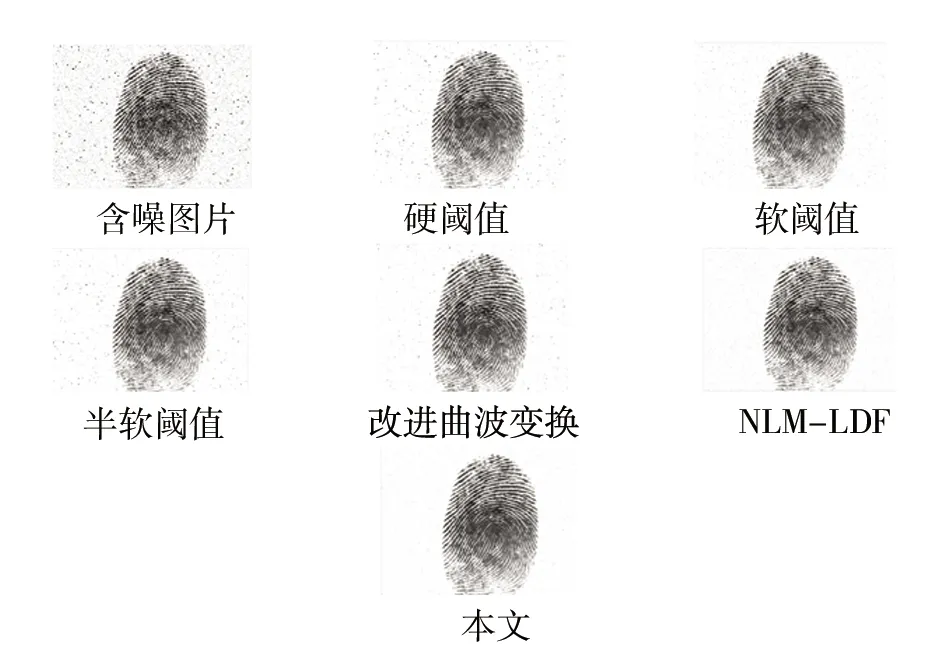
图5 不同算法对含混合噪声的107_3.tif图像的去除效果

图6 不同算法对含混合噪声的109_5.tif图像的去除效果

由以上的三幅噪声去除效果图可知，本文算法对比其他五种算法来看对含有混合噪声的指纹图像中的椒盐噪声去除的效果要更好。

为了对该算法的有效性进行更精确的度量，选用峰值信噪比(PSNR)和均方误误差(MSE)作为客观的评价指标，其计算公式如下

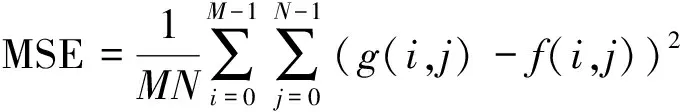
(8)

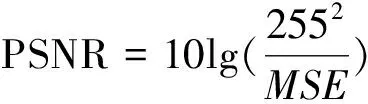
(9)

式(8)中，

f

(

i

,

j

)为原始图像，

g

(

i

,

j

)为去噪后的图像。评价去噪质量时，如果得到越大数值的峰值信噪比，越小数值的均方误差，就表明该算法对噪声去除越彻底。

不同算法对三幅指纹测试图像去噪后的PSNR和MSE如下表1所示。

表1 不同算法对三幅添加混合噪声指纹图片去噪后的评价指标

表1中1和2行、3和4行、5和6行的数据是分别六种算法对101_2.tif图片、107_3.tif图片和109_5.tif图片处理后得到的峰值信噪比和均方误差。由表1数据可知，三幅添加了相同方差高斯噪声和相同密度椒盐噪声的指纹图像101_2.tif,107_3.tif,109_5.tif,用本文算法进行混合噪声去噪时，得到的峰值信噪比和均方误差都有所改善。相比于经典硬阈值、软阈值、半软阈、改进曲波变换和NLM-LDF算法对混合噪声进行去噪时，指纹图像101_2.tif峰值信噪比分别提高了5.33%、4.00%、4.44%、3.00%，2.34%，均方差分别降低了2.9×10dB、1.9×10dB、2.4×10dB、1.0×10dB、0.9×10dB。指纹图像107_3.tif的峰值信噪比分别提高了6.10%、5.35%、5.57%、2.32%、1.87%，均方差分别降低了3.8×10dB、 3.1×10dB、 3.3×10dB、 1.0×10dB， 0.9×10dB。指纹图像109_5.tif的峰值信噪比分别提高了5.66%、4.77%、5.02%、2.48%、1.88%，均方差分别降低了3.4×10dB、 2.7×10dB、2.9×10dB、0.9×10dB、0.7×10dB。

为了验证该算法的去噪效果与添加混合噪声密度之间的关系，分别对指纹图像109_5.tif添加方差为0.02的高斯噪声和密度为0.02的椒盐噪声的混合噪声、方差为0.03的高斯噪声和密度为0.03的椒盐噪声的混合噪声、方差为0.04的高斯噪声和密度为0.04的椒盐噪声的混合噪声时，不同算法的峰值信噪比和均方误差效果如下表2所示。

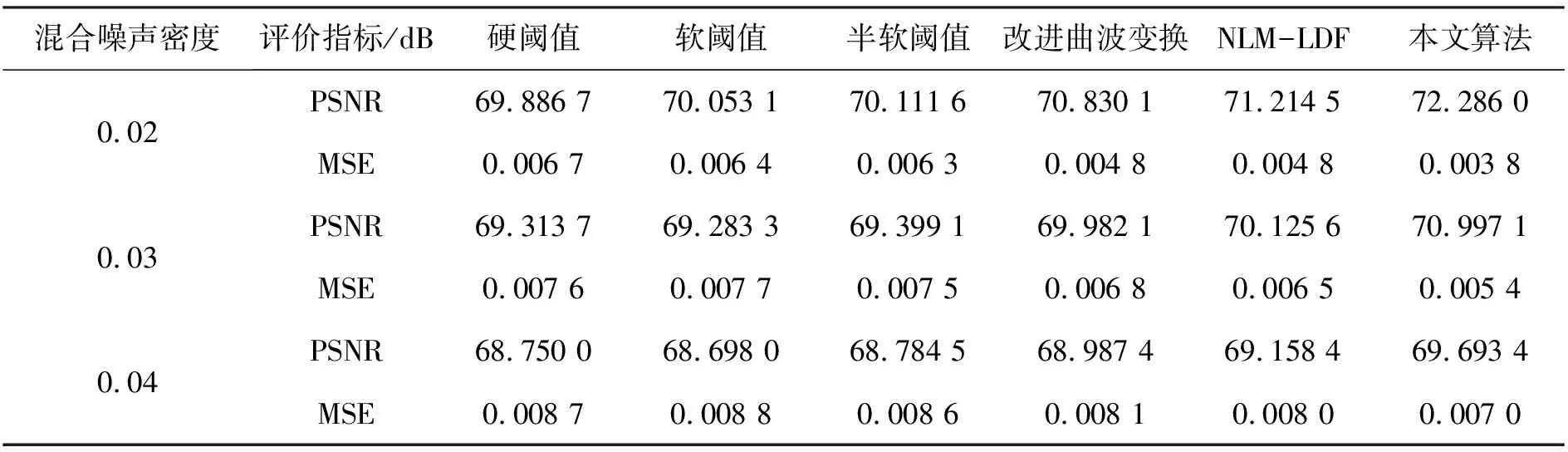
表2 不同算法对添加了不同密度的混合噪声109_5.tif去噪效果

表2里面1～2行、3～4行、5～6行分代表各个算法对添加噪声密度为0.02、0.03、0.04的109_5.tif指纹图像进行噪声去除后得到的峰值信噪比和均方误差。由表2的数据可知，随着添加混合噪声密度的增大，各个算法对指纹图像109_5.tif去噪效果都有所下降，但是本文算法相比于其他算法对混合噪声的去除效果仍旧有所提升。

FCV2004指纹数据库中总共有四个库，分别是DB1、DB2、DB3、DB4。四个数据库里面指纹图像的区别在于采集指纹的传感器的不同。为了使得本文算法的效果更有可信度，选取使用交叉匹配的光学传感器“V300”采集的指纹数据库DB1和使用Digital Persona提供的光学传感器“U.are.U 400”采集的指纹数据库DB2的所有指纹图片分别进行不同算法的噪声去除工作。其中DB1和DB2数据库里面分别含有80张指纹图片，对每一幅图像噪声去除工作后取数据的均值。六种算法对添加了相同密度两个数据库指纹图像去噪效果如表3所示。

表3 不同算法对添加了相同密度两个数据库指纹图像去噪效果

表3里1～2行、3～4行行分代表在DB1和DB2进行噪声去除后得到的峰值信噪比和均方误差。对比了不同算法在DB1和DB2两个指纹数据库进行噪声去除工作后。由表3可知，本文算法较其他算法仍然保持较好的去噪效果。总的来说，本文算法略优于中值滤波，主要是因为中值滤波对混合噪声中的高斯噪声去除效果不好，本文算法优于其他五种算法是因为它采用的自适应阈值较好地解决了全局阈值对噪声信号的误判，连续型低误差阈值函数拥有更好的连续性并且极限时误差趋于0。由以上的数据可知本文算法无论在视觉还是客观指标上相比于传统算法都有所提高。

4 结论

为了解决传统的小波阈值算法对含有混合噪声的指纹图像噪声去除不彻底的问题，本文提出了一种自适应阈值和连续型低误差的CALE阈值函数的小波去噪算法。实验选用FCV2004数据库中的三幅指纹图像作为测试图像，用该算法对比其他五种算法进行了多次的对比实验。实验结果表明，无论是从主观视觉还是客观评价指标来看，该算法明显优于其他五种去噪算法，表明了本文算法能够有效地去除指纹图像里的混合噪声，算法的设计方案是有效的、可行的。