新夹层梁理论及其有限元分析

吴建强

(安徽理工大学力学与光电物理学院，安徽 淮南 232001)

夹层结构由于具有良好的隔声隔热和吸收冲击能力、强度高、刚度大等优点，已广泛应用于航空航天、海事、交通、土建等工程领域。但针对夹层结构的理论研究，目前主要有Reissner理论、Hoff理论。Reissner理论将约束层看作薄膜，只能承受面内力，不能承受弯曲，因而夹心层内部产生弯曲应力；Hoff理论虽然把约束层看成了普通的薄板，考虑了弯曲变形的影响，但只考虑了横向剪力。文献[6]认为夹层结构横向应变沿厚度成抛物线变化；文献[7-8]基于高阶理论得到夹层板的自由振动的解析解；文献[9]分析了经典复合材料夹层板自由振动特性；文献[10-13]等的研究通过假定所有轴向、弯曲由上下层承受，中间层仅承受横向荷载；文献[14]分析了功能梯度夹层梁振动方程，没有考虑横向压缩产生的影响；文献[15]研究了软芯夹层梁横向剪切力应力公式，公式推导过程中引入了平面假设；文献[16]假定夹层结构横向应变沿厚度方向呈抛物线分布，发展了一种计算复合材料板的变形理论解。文献[17] 将夹层结构的上下层视为薄膜，忽略其抗弯刚度，同时认为中间夹层只承受横向剪力作用，分析了夹层结构的相应问题。文献[18]将夹层结构上下层视为薄板，中间层仍只考虑横向剪力，进一步对夹层结构进行了研究。

在已有的研究文献中，计算夹层结构时都在不同程度上引入了平面假设或者忽略了中间夹层的横向可压缩性，当用这些理论来求解短、粗或软夹层梁时误差大。本文将发展一种新型梁单元，摒弃平面假设，同时考虑横向可压缩性，给出了物理方程、几何方程的详细推导过程，利用最小势能原理得到平衡方程，与经典欧拉梁理论解和有限元结果进行对比分析，为软夹层横向位移计算提供一种参考。

1 新夹层梁基本理论

1.1 基本假设

对由上约束层、夹心层和下约束层组成的三夹层梁，假设如下：

1)两约束层为欧拉梁；

2)各层有独立的横向和轴向位移，夹心层横向和轴向位移在厚度方向上二次变化；

3)层间无相对滑动；

4)考虑中间夹层正应力，正应变，剪应力，剪应变。

1.2 位移场

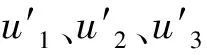
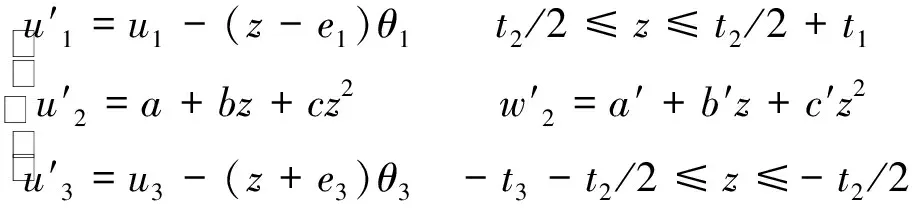
(1)

式中：

a

、

b

、

c

、

a

′、

b

′、

c

′为常数，

e

=(

t

+

t

)

/

2，

e

=(

t

+

t

)

/

2。

图1 夹层梁示意图

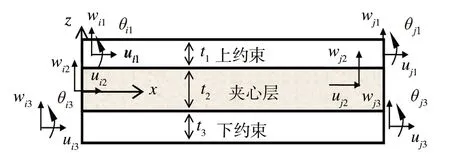
图2 两结点16自由度夹层梁单元

由层间无相对滑动假设，有

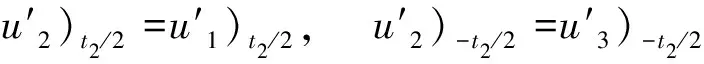
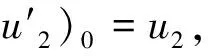
(2)

将公式(2)代入公式(1)得

(3)

(4)

夹心层位移表示为

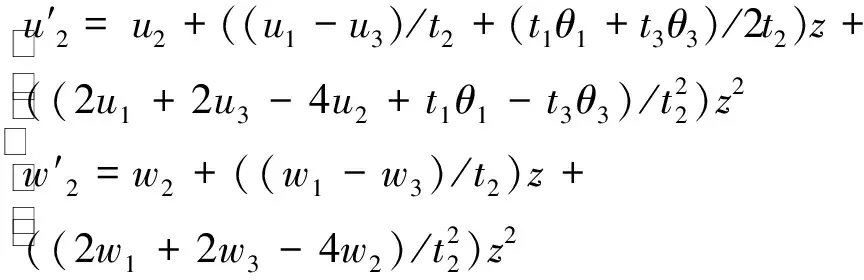
(5)

1.3 几何方程

由公式(1)及公式(5)得夹层梁各层应变-位移关系。

上约束层

(6)

下约束层

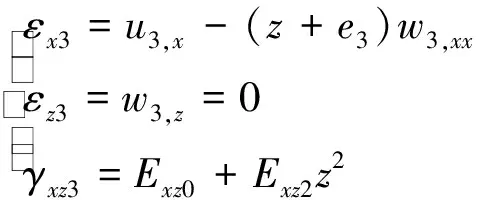
(7)

夹心层

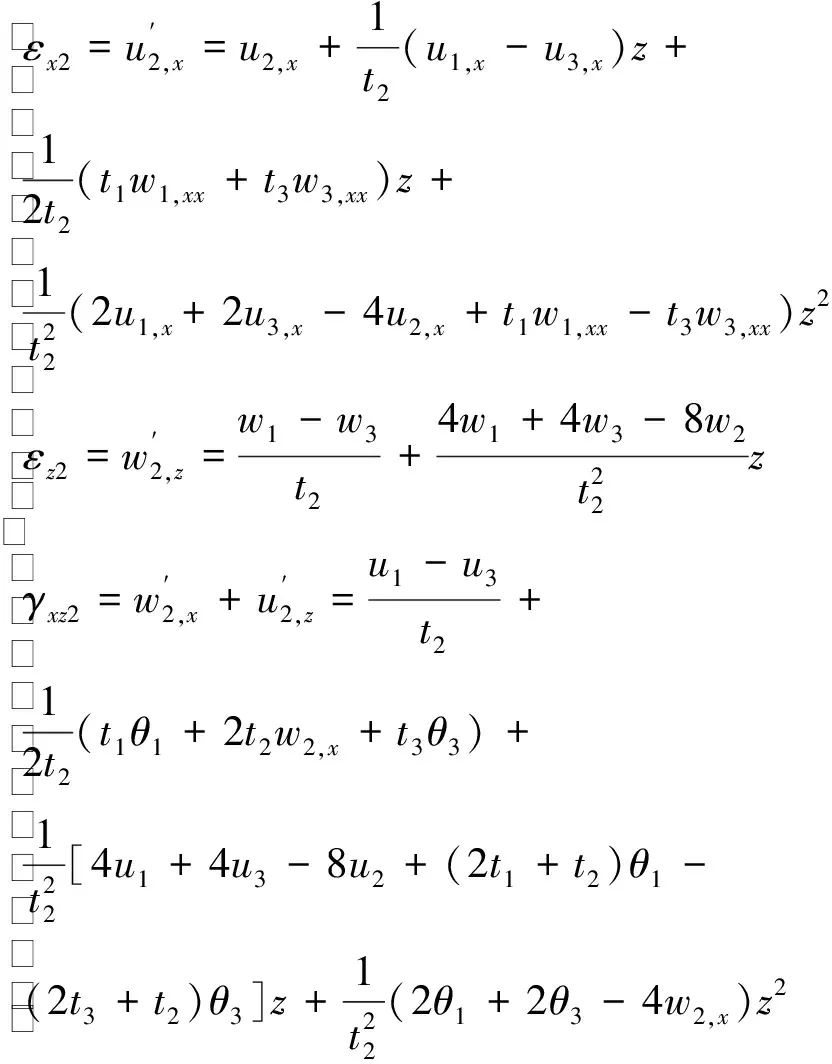
(8)

式中：(·),表示变量(·)对

x

求一阶导数，

ε

1、

ε

、

ε

1、

ε

3、

γ

1、

γ

3、

ε

2、

ε

2和

γ

2分别是上下约束层和夹心层的轴向、横向应变和剪切应变。

1.4 本构关系

夹层梁第

k

层粱的本构关系为{

σ

()}=[

C

()]{

ε

()}

(9)

其中，[

C

()]为弹性常数矩阵。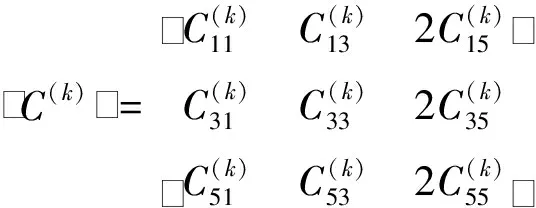

1.5 系统应变能

夹层梁应变能为

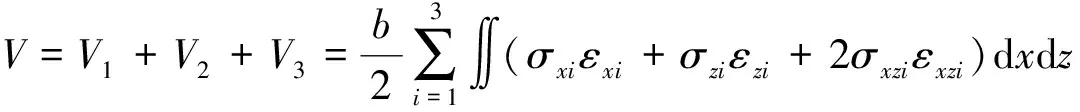
(10)

式中：

V

、

V

、

V

分别是上约束层、夹心层和下约束层应变能，

b

为梁宽度。

2 有限元的实现

2.1 单元位移模式

单元的自由度如图2所示。小变形情况下，上下约束层位移设为

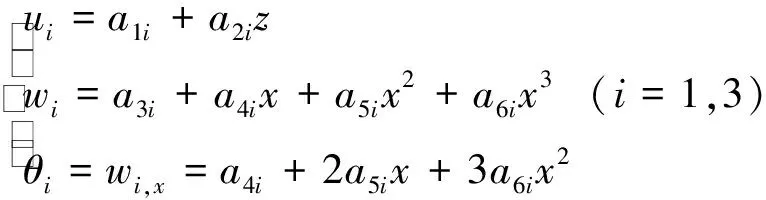
(11)

设夹心层位移函数为

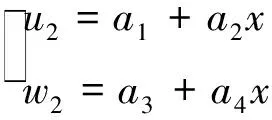
(12)

将两端点的位移分量和坐标代入公式(11)、(12)，可得待定系数，从而得到各层中面位移和任意点位移场分别为

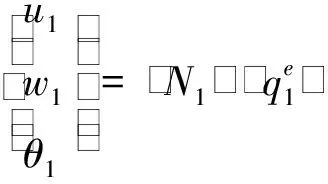
(13)

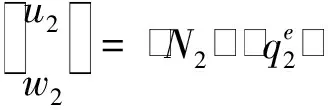
(14)

(15)

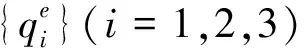
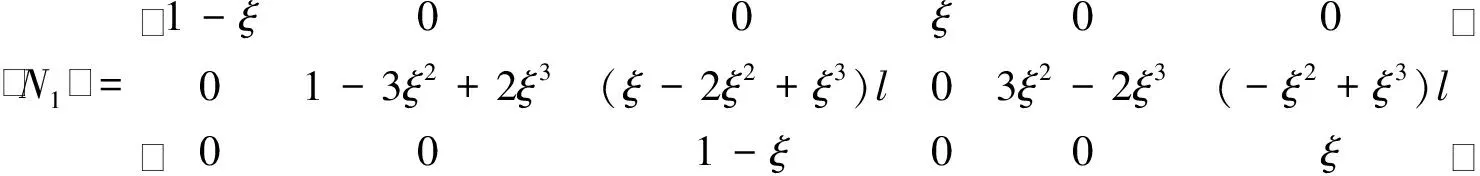
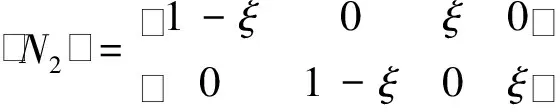
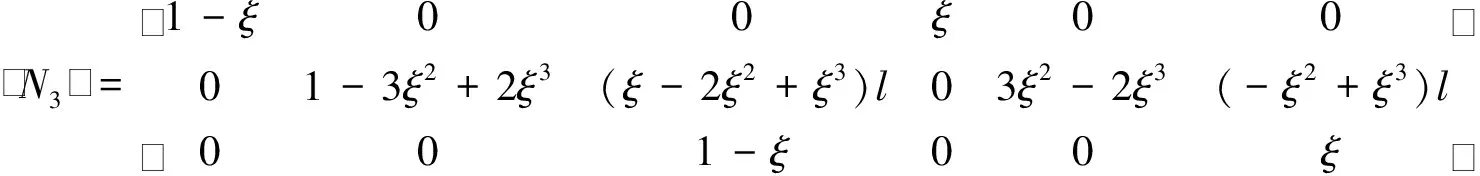
ξ

=

x/l

,

l

是单元长度。

2.2 单元平衡方程和刚度矩阵

单元应变能为

{

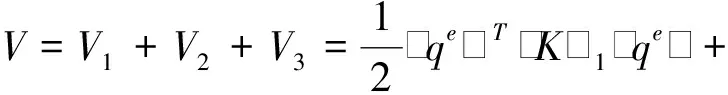
q

}[

K

]{

q

}

/

2

(16)

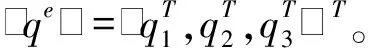
单元外力势能为

W

=-{

q

}{

F

}

(17)

其中：{

F

}表示外力列阵。

故单元总势能为

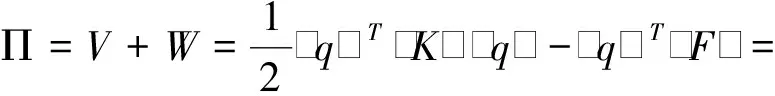
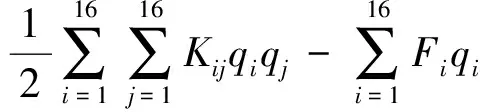
(18)

由最小势能原理，得单元平衡方程

{

F

}=[

K

]{

q

}

(19)

3 数值验证

3.1 与解析解比较

长为

l

的悬臂梁，在自由端受集中力

F

作用，由材料力学知识有，悬臂梁在自由端受集中力的挠曲线为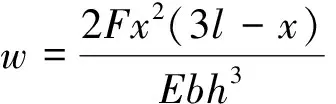

式中：

x

为所求截面到固定端的距离，mm；

b

为梁的宽度，mm；

h

为梁的厚度,mm。夹层梁长度为2 000mm,宽度为50mm,总厚度为100mm,约束层厚度100(1-

r

)/2，夹层厚度为

r

,%。模型

I

为经典欧拉梁，约束层和夹心层材料相同，其弹性模量为72GPa,泊松比为0.3，材料密度为2.7×10t/mm。表1给出了

r

=10%、30%、50%、80%、100%，

F

=2 000N时自由端挠度对比情况。从中可以看出，对于不同厚度的夹心层，本文方法的结果与经典欧拉梁的理解论相差非常小，相对误差都在0.02%以内，验证了本文方法的合理性。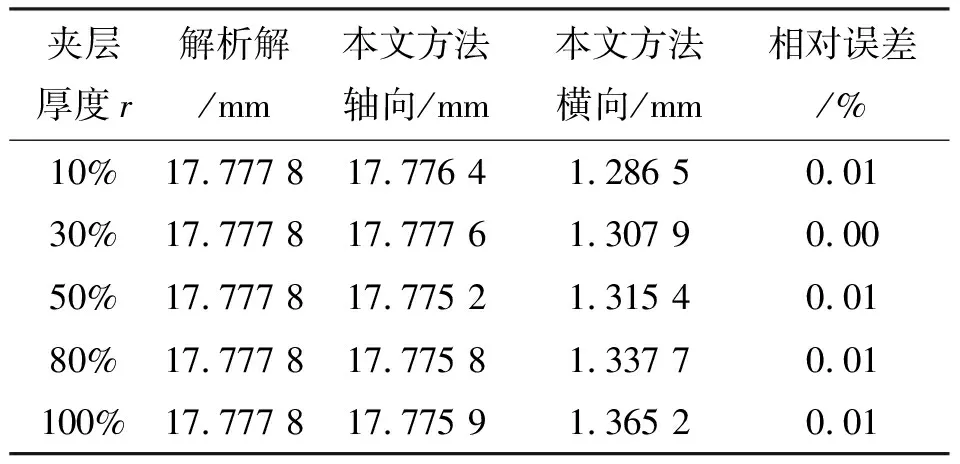

表1 模型(Ⅰ)的本文方法与解析解的结果比较

图3对比了夹层厚度为80%时梁内各点位移对比情况，经典欧拉梁各层在同一横截面上的位移相同，而本文方法的每一层是有其独立横向位移的，得到的每一层的横向位移是不同的(见端部局部放大图)，力作用在上约束层时，上约束层的横向位移值最大，下约束层的最小。

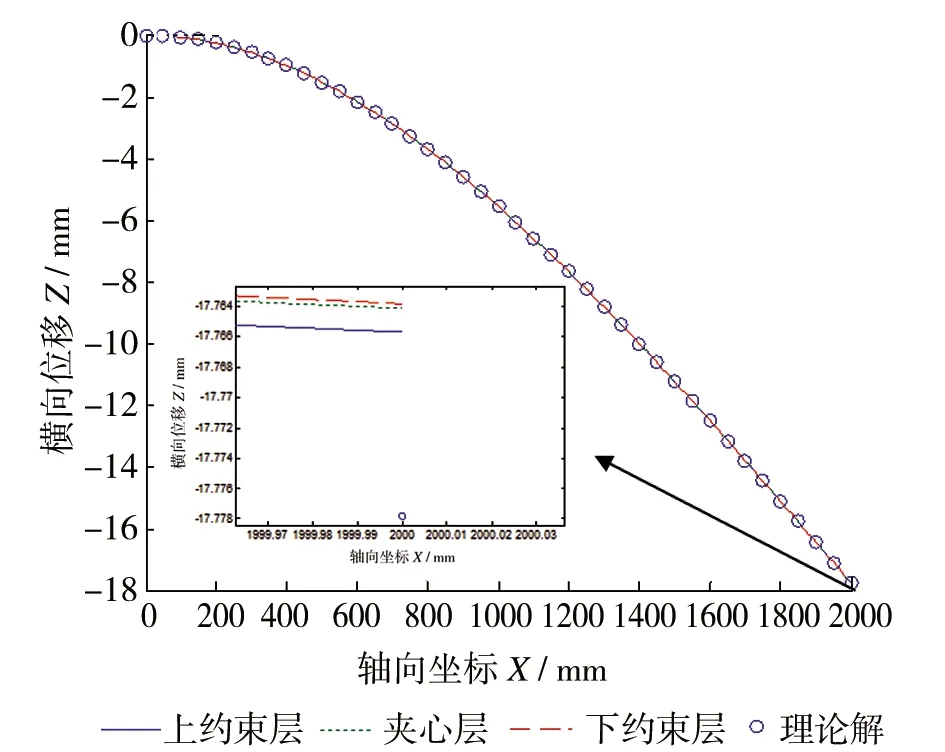
图3 模型(Ⅰ)r=80%本文与欧拉梁结果对比图

3.2 与有限元结果比较

经典欧拉梁没有考虑梁的泊松效应和横向可压缩性，当两者对梁的影响较大时，采用经典欧拉梁理论来求解是不精确的，对夹层梁特别是夹心层和约束层的材料参数差异较大，即夹心层较软时，经典欧拉梁模型求解的误差更大。目前，针对该问题多用有限元法分析，有限元法能准确求解夹层梁问题，为了验证本文方法的正确性，有限元法和本文法所取梁的参数如下：梁的长度为2 000mm,宽度为50mm,总厚度为100mm，约束层弹性模量为72GPa,泊松比为0.3，材料密度为2.7×10t/mm；夹心层材料弹性模量为10MPa，泊松比为0.49，材料密度为1.3×10t/mm，

r

=80%。计算模型(Ⅱ)取图4两种边界情况，图4(a)是悬臂梁模型，在自由端的上约束层作用集中力

F

=100N；图4(b)是两端固定模型，在夹层梁的中间位置作用集中力

F

=100N，图4(c)给出了三维有限元模型。其对比结果如表2、图5和图6所示。

从表2可以看出，对悬臂夹层梁，本文方法得到的结果跟三维有限元结果一致，上约束层、夹心层和下约束层的自由端的最大挠度值与三维有限元结果相比，误差很小，分别为0.05%、0.03%和0.03%，说明该理论是正确的。

(a)悬臂夹层梁 (b) 两端固支夹层梁 (c)三维有限元模型图4 模型(II)计算模型

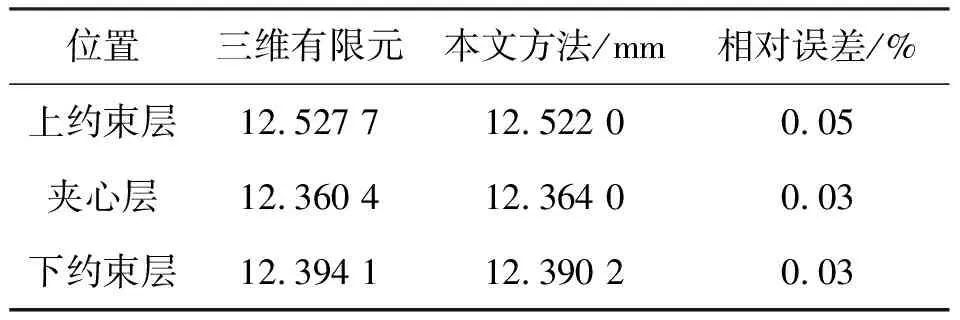
表2 悬臂梁模型最大挠度对比

(a)轴向位移

(b)横向位移

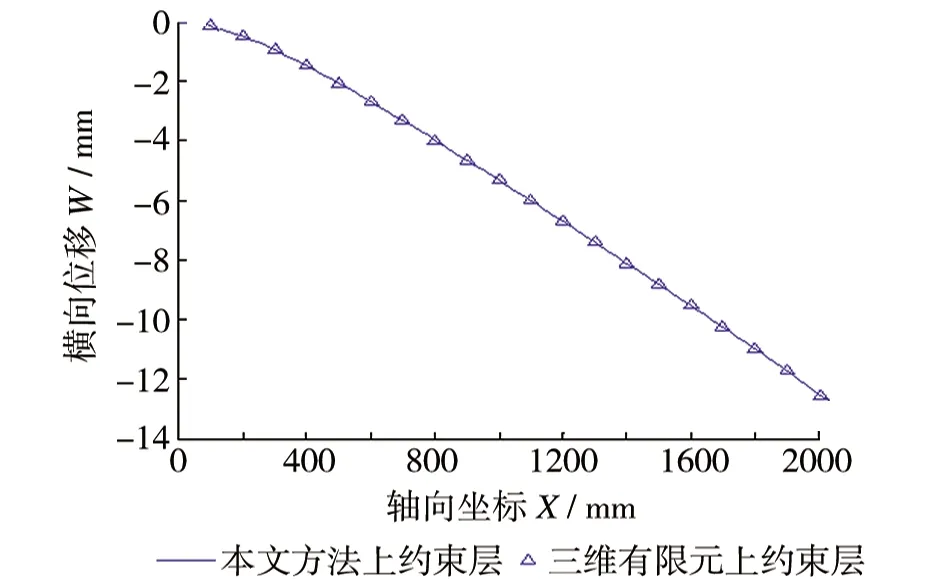
(c)上约束层横向位移

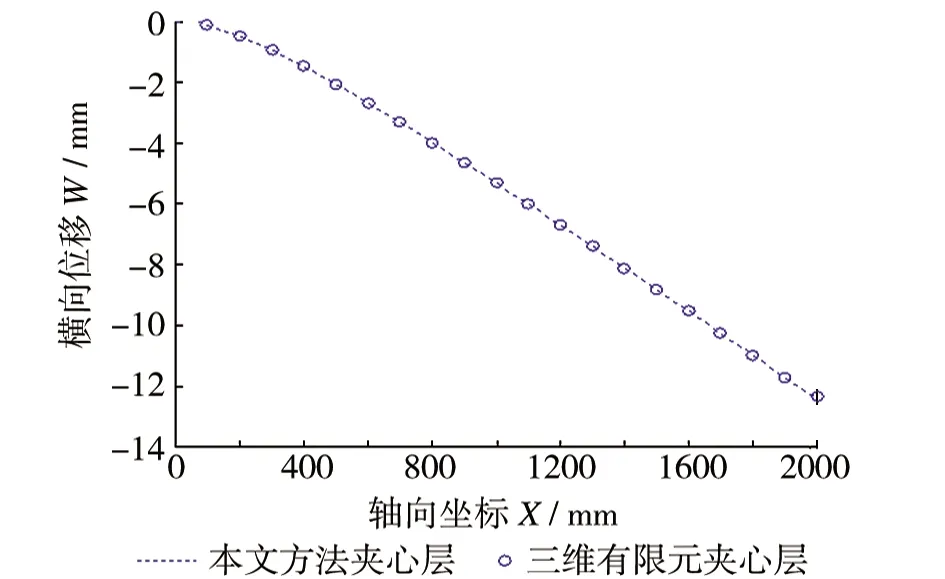
(d)夹心层横向位移

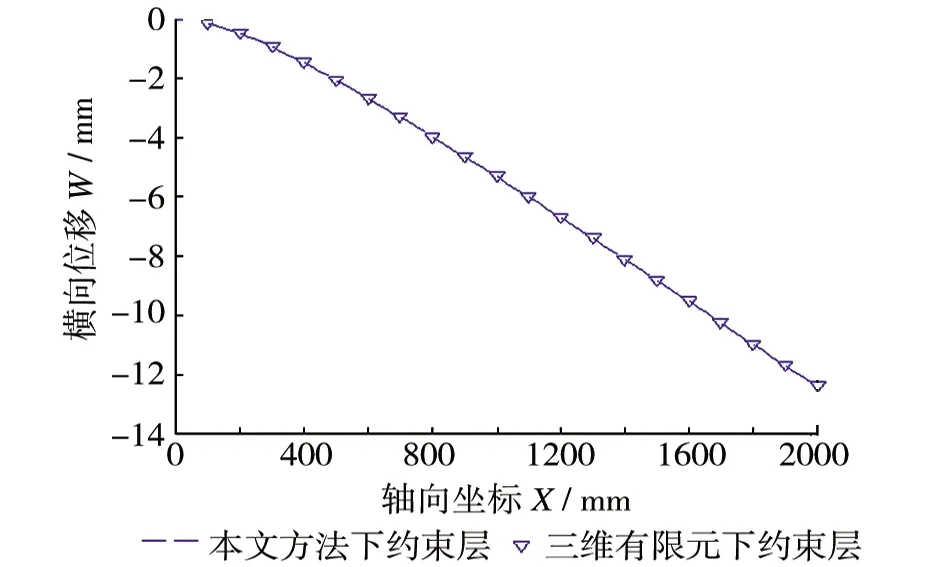
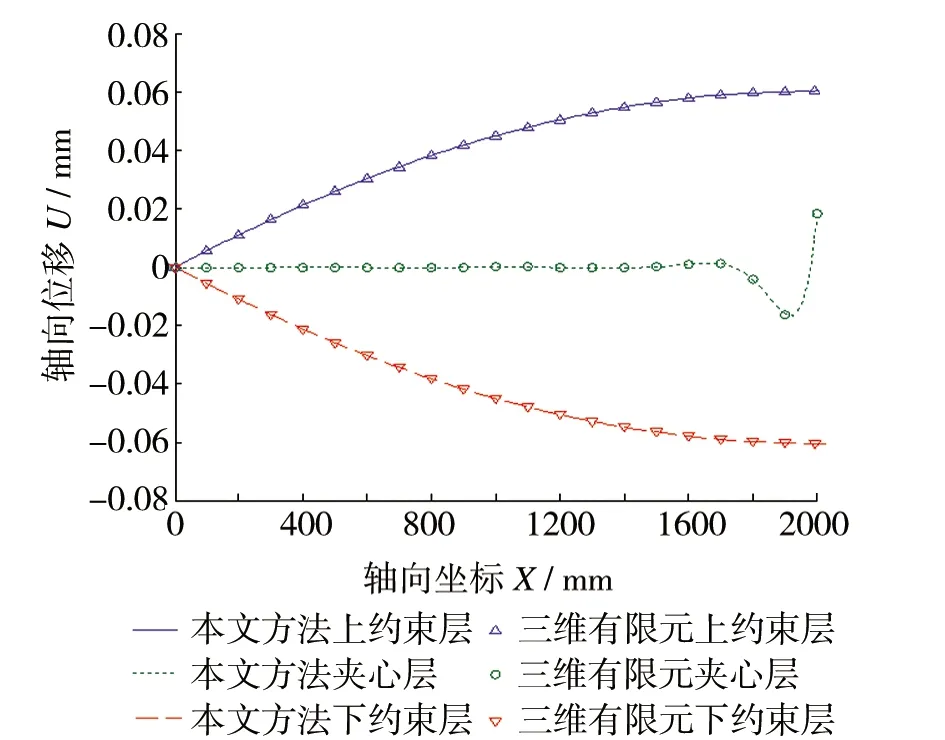
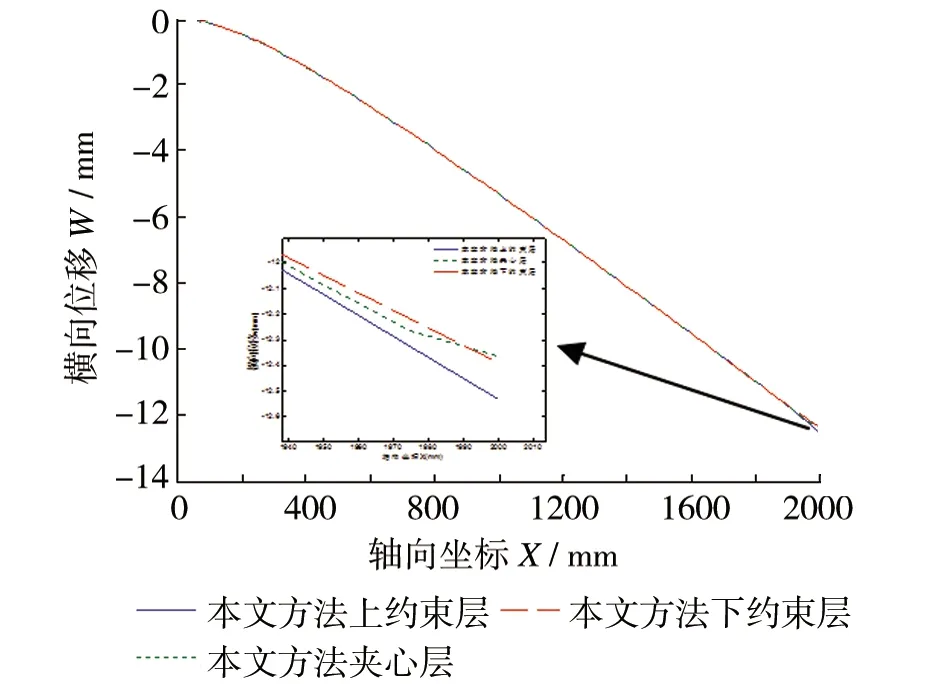
(e)下约束层横向位移图5 模型(II)悬臂夹层梁计算结果

图5分别对比了模型(II)悬臂梁与本文方法横向位移和轴向位移情况，图5(a)～图5(b)分别对比了轴向位移和横向位移，本文得出的结果跟三维有限元结果一致，横向力

F

作用下，夹心层的材料相对较软、 刚度较小， 夹心层端部区域为明显受压状态， 因此上约束层的横向位移会比下约束层的横向位移要大，大概在梁长度93%～100%之间即

F

作用端点附近三层的变形差别相对较大。图5(c)～图5(e)对比了各层横向位移变化情况，在93%～99.5%区间上，上约束层的横向位移最大，夹心层次之，下约束层最小，表现为夹心层受压；在99.5%～100%区间上约束层的横向位移最大，下约束层次之，夹心层最小，表现为夹心层几何中心线以上的夹心层部分受压，中心线以下的夹心层受拉；夹心层在受压状态下，自由端端部是没有约束的，所以端部前缘的夹心层会向轴向正方向运动，从图5可以看出，本文方法得出的结果与有限元结果相比，误差都很小。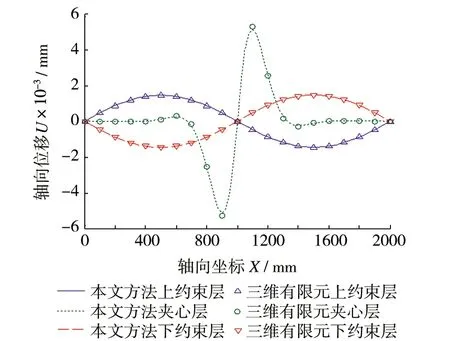

(a)轴向位移

(b)横向位移

(c)上约束层横向位移

(d)夹心层横向位移

(e)下约束层横向位移图6 模型(II)两端固定夹层梁计算结果

图6(a)～图6(b)对比了两端固定夹层梁有限元法和本文方法在轴向位移和横向位移的情况； 从图6(a)可以看出， 两端固支夹层梁在横向集中力作用下， 力

F

作用点附近的夹心层是处于被压缩状态，力作用点处压缩量最大，此处的夹心层会以作用点为中心向两边移动； 从图6(b)得出， 中间层较软， 作用点附近区域会呈现明显受压状态，因此上约束层的横向位移会比下约束层的横向位移要大；
图6(c)～图6(e)分别对比了上约束层、 夹心层和下约束层横向位移，在距离力

F

的作用点0～100mm之间三层的横向位移差别相对较大，在力作用点处，三层的横向位移均达到最大值， 分别为1.882 5mm、 1.861 9mm和1.848 2mm。

由图5和图6可看出，对于夹心层相对约束层较软的梁，因剪切作用和泊松效应所产生的影响是存在的，夹层梁的上约束层受压，下约束层受拉，上下约束层的轴向变形基本呈反对称趋势。通过对比，用本文方法计算夹心层较软的夹层梁模型并跟三维有限元方法的结果比较，结果表明本文方法克服了经典方法的不足，能准确地体现夹层梁在精力作用下，截面变形后不再是一个平面，横向方向是可压缩的。

4 结论

本文给出了一种用于夹层梁结构计算的梁单元。该模型摒弃了平截面假定以及变形过程中厚度保持不变的假设，算例验证了本文方法的正确性。同时，该思想也可进一步发展用于具有多夹层的夹层梁、板和壳。

本文仅验证了模型的静力学响应的正确性，对实际工程问题而言仅仅考虑静力学问题是不够的，实际结构中常作用有动载荷，下一步将对结构的振动特性和动力学响应问题进行研究，以确定结构的动力学特性和承载能力，为改善结构的动力学性能提供重要依据。