基于Petri网的物流派送模型修复分析
方贤文,杨慧慧,邵叱风
(安徽理工大学数学与大数据学院,安徽 淮南 232001)
流程挖掘是一门介于计算智能和数据挖掘以及过程建模和分析之间的新兴研究学科,流程挖掘的起点是事件日志,所有流程挖掘技术都假设有可能顺序地记录事件,使每个事件指向一个活动,并与特定的案例(即流程实例)相关。流程挖掘主要包括三个领域:流程发现、一致性检查和流程增强。最近新兴的模型修复领域,也算是流程增强的一种。本文的研究侧重于一致性检查与模型修复。
一致性检查是将现有流程模型与同一流程的事件日志进行比较。一致性检查可以用来检查记录在日志中的事实是否符合模型。文献[5]中针对声明性模型提出了一种新的一致性检查方法,文中采用了基于对齐的方法,以便能够处理声明式模型固有的灵活性带来的巨大搜索空间。文献[6]中提出了一种检验序列图与状态图一致性的方法。在比较过程模型和事件日志有不同的质量维度,例如适应度、简单性、精度和泛化。而在本文中,我们关注于适应度:一个具有良好适应性的模型允许在事件日志中看到的大多数行为。如果日志中的所有轨迹都能被模型从头到尾重复播放,那么模型就具有完美的适用性。
模型修复主要针对事件日志与原始模型不符合的部分进行修复,最大程度地与原始模型保持相似。文献[9]将一致性检查的信息用于模型修复,识别流程模型中已删除活动的结构、附加活动和邻接活动之间的关系以及流程模型中的不一致子流程,基于文中所提出的技术实现模型修复。文献[10]使用一个现有的一致性检查器,将日志分解为不匹配子迹的几个子日志,并对每个子日志派生出一个子流程,最后将其添加到原始模型的适当位置,从而达到修复一个流程模型的目的。文献[11]主要致力于一种模型分解修复工具,分解后的模型修复是模型增强的一种方法。模型修复可以使得事件日志与流程模型有较高的适合度甚至完美适合度,因此,越来越多的学者致力于研究模型修复。
在已有的方法中最为经典的修复方法之一是插入-跳过活动修复法,此方法对于单个日志移动来说比较容易理解和使用。但是,在大多数情况下会见到连续的日志移动,那么在同一个位置单个的插入多个活动事件,会构成模型的繁琐。因此,在已有的子流程修复算法的基础上,本文针对含有连续日志移动的流程模型修复问题,提供了一种用于辅助模型修复的有效寻找日志移动可修复的库所集的算法。从成本对齐的角度出发,根据检测到的日志移动部分借助于该算法可有效实现模型修复。
1 基本概念
定义1
(变迁发生规则)一个网系统是一个标识网∑=(P
,T
;F
,M
),并具有下面的变迁规则(1)对于变迁t
∈T
,如果∀p
∈P
∶p
∈t
→M
(p
)≥1则说变迁t
在标识M
有发生权,记为M
[t
>。(2)若M
[t
>,则在标识M
下,变迁t
可以发生,从标识M
发生变迁t
得到一个新的标识M
′(记为M
[t
>M
′),对∀p
∈P
,
定义2
(迹,事件日志)设Φ是一组活动名称集合,若α
∈Φ是一个活动序列,则称α
是一条迹。若L
∈B
(Φ)是迹的有限非空的多重集,则称L
是一个事件日志。定义3
(对齐)设N
=(P
,T
,F
,α
,m
,m
)是一个Petri网,设α
=a
a
…a
是一条迹,α
到流程模型N
之间的对齐γ
=(a
,t
)(a
,t
)…(a
,t
)是满足下列条件的移动序列:(1)对齐γ
的第一行(a
,a
,…,a
)是事件日志中的一条迹;(2)对齐γ
的第二行(t
,t
,…,t
)是Petri网流程模型N中的一组变迁发生序列;(3)对于所有的i
=1, 2, …,k
, 如果t
≠≫,α
(t
)≠τ
,且a
≠≫,那么α
(t
)=a
。这里的移动对满足以下条件:
(1)如果a
=≫∧t
≠≫,则称为模型移动;(2)如果a
≠≫∧t
=≫,则称为日志移动;(3)如果a
≠≫∧t
≠≫,则称为同步移动;定义4
(最优对齐)给定一条迹α
和Petri网流程模型N
, 对于α
和N
之间所有的对齐χ
, ∃γ
∈χ
,对∀γ
′∈χ
,都有c
(γ
)≤c
(γ
′)。则称γ
是α
和N
之间的最优对齐。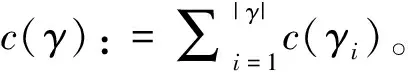
定义6
(行为轮廓)设(N
,M
)是一个网系统,初始标识为M
,对任给的变迁对(x
,y
)∈T
×T
满足以下关系:(1)若x
>y
且y
≯x
, 则称为严格序关系, 记作x
→y
;(2)若x
≯y
且y
≯x
,则称为排他关系,记作x
+y
;(3)若x
>y
且y
>x
, 则称为交叉序关系, 记作x
‖y
;(4)所有关系的集合称为网系统的行为轮廓,记作BP
={→,+,‖}。2 物流派送流程模型的一致性检查
随着国民经济的快速发展,社会物流需求也显著增加,我国物流工程发展迅速。表1是从某物流公司派送包裹记录中调取的部分事件日志,表2是各个字母所代表的活动事件。

表1 记录的事件日志
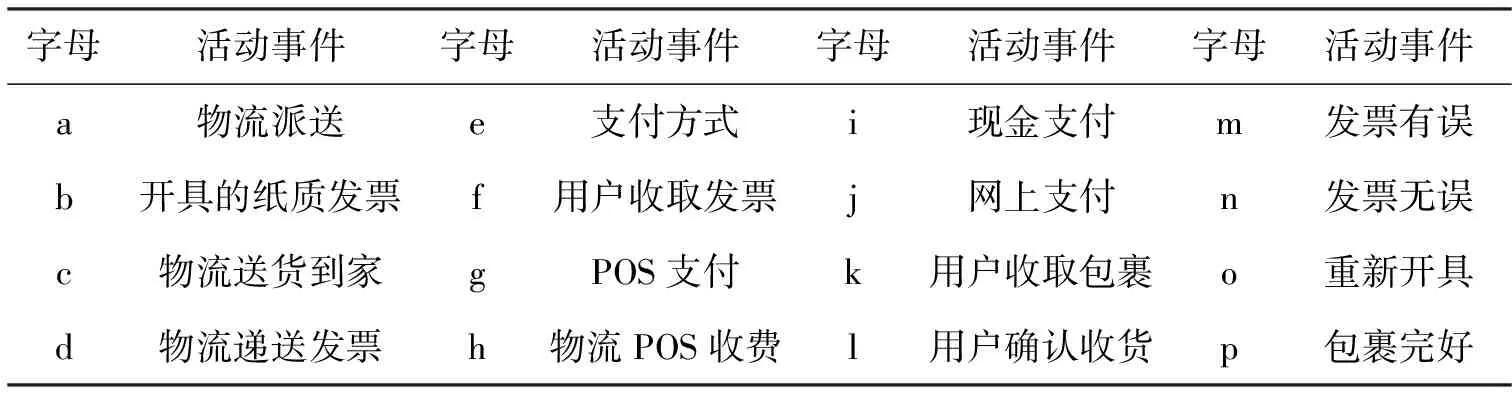
表2 各个字母所代表的活动事件
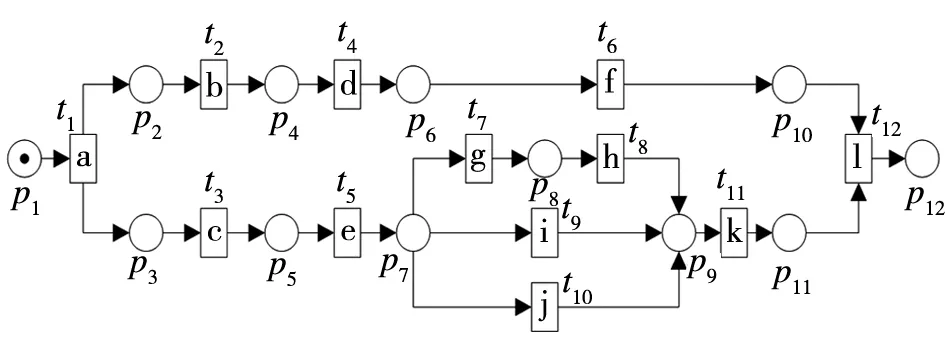
图1 基于Petri网的物流派送流程模型N
由表1提供的事件日志,得到合并后的迹及实例数为
α
=〈a,b,d,c,e,f,j,k,l〉,α
=〈a,c,b,e,d,f,g,h,k,l〉,α
=〈a,b,c,d,f,e,i,k,l〉,α
=〈a,c,e,b,d,n,f,j,k,l〉,α
=〈a,b,c,d,m,o,f,e,j,k,l〉,α
=〈a,b,c,p,e,d,g,h,m,o,f,k,l〉,α
=〈a,b,d,c,n,f,e,i,k,l〉。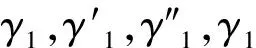
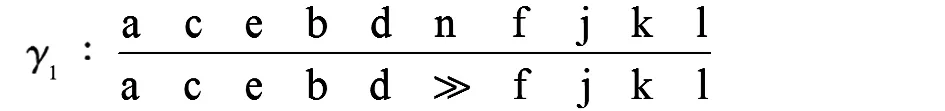
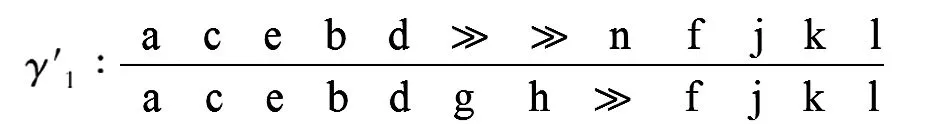

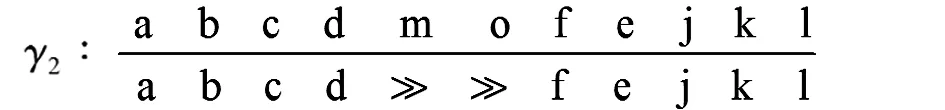

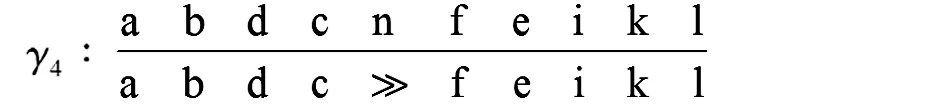
3 流程模型修复分析
(1)寻找日志移动的可修复库所集
通过事件日志与流程模型的一致性检查,可以看到迹α
、α
、α
、α
与流程模型之间存在偏差,偏差成本分别为1,2,3,1,因此,要想让流程模型能够重放所有的迹,必须要对流程模型进行修复。根据迹与流程模型之间的最优对齐,可以很明显地看出需要修复的部分属于日志移动。对于单个日志移动的修复,可以采用经典的“插入和跳过活动”的方法对模型进行修复,然而有些日志移动是连续出现的,此时可以根据文献[13]中提到的基于子流程的修复算法进行模型修复。这种对单个日志移动或者连续日志移动进行模型修复的方法,都是需要插入相应的活动事件。因此在修复之前,寻找最适合插入活动事件的库所也是一个关键环节。在选择适合被插入的库所方面,文献[13]中有简单描述,但并没有给出具体形式的算法,因此,本文针对单个日志移动或者连续日志移动在进行模型修复时如何选择对应库所做了一个算法补充,算法如下
算法1:寻找日志移动的可修复库所集
输入:日志中所有的最优对齐γ
,γ
,…,γ
;一个Petri网流程模型N
输出:日志移动的可修复库所集P
Step1设p
为初始库所,γ
[]为第i
个对齐中第j
个移动对,P
[]为第i
个对齐中第j
个移动对所对应的库所,m
为初始标识。Step2如果γ
[]是一个日志移动,则P
[]=(p
);否则,m
[π
(γ
[])>m
,在m
状态下有m
(p
)=…=m
(p
)=1,那么P
[]=(p
,…,p
).
Step3当2≤j
≤|γ
|时,如果γ
[]是日志移动,则P
[]=P
[-1],若γ
[],γ
[+1],…,γ
[+]是连续的日志移动,则有P
[]=P
[+1]=…=P
[+].
Step4当2≤j
≤|γ
|时,如果γ
[]不是日志移动,则m
[-1][π
(γ
[])>m
,在m
状态下,m
(p
)=…=m
(p
)=1,则P
[]=(p
,…,p
),然后执行Step5.Step5每一个对齐中,只保留日志移动对中对应的P
[],然后删除其余移动对所对应的库所。Step6观察所有保留的日志移动对,如果不同对齐中有相同的日志移动,即γ
11=γ
22=…=γ
,其中1≤it
≤s
,1≤jf
≤|γ
|,那么若P
[11]∩P
[22]∩…∩P
[]=P
′≠∅,则更新这些日志移动的库所表示为P
,即P
[11]=P
[22]=…=P
[]=P
′;否则,若交集为空集,则无需变动。然后执行Step7.Step7整理保留下来的库所集P
[],得到一个日志移动的可修复库所集P
={P
[]}算法结束。根据上述算法,寻找最优对齐γ
,γ
,γ
,γ
中日志移动所对应的可用于修复的库所集。首先输入四个最优对齐γ
,γ
,γ
,γ
和Petri网流程模型N
,第一步交代了字母所代表的含义和初始状态m
(p
)=1;第二步表示在一个最优对齐中,第一个移动对若是日志移动,那么它所对应的可修复库所为P
[]=(p
),否则按照正常的变迁发生规则依次触发后面的活动事件;第三步说明了出现连续日志的情况下,对应可修复库所是相同的;第四步表示在依次寻找最优对齐中所有移动对所对应的库所,对最优对齐γ
,γ
,γ
,γ
的执行结果为γ
[1]=〈a
,a
〉,P
[1]=(p
,p
);γ
[1]=〈c
,c
〉,P
[1]=(p
,p
);…;γ
[1]=〈d
,d
〉,P
[1]=(p
,p
);γ
[1]=〈n
,≫〉,P
[1]=P
[1]=(p
,p
);…;γ
[2]=〈m
,≫〉,P
[2]=(p
,p
);γ
[2]=〈o
,≫〉,P
[2]=P
[2]=(p
,p
);…;γ
[3]=〈p
,≫〉,P
[3]=(p
,p
);…;γ
[3]=〈m
,≫〉,P
[3]=(p
,p
);γ
[3]=〈o
,≫〉,P
[3]=P
[3]=(p
,p
);…;γ
[4]=〈n
,≫〉,P
[4]=(p
,p
);…;γ
[4]=〈l
,l
〉,P
[4]=(p
);第五步是只保留了日志移动对所对应的库所,此时的执行结果为:γ
[1]=〈n
,≫〉,P
[1]=(p
,p
);γ
[2]=〈m
,≫〉,P
[2]=(p
,p
);γ
[2]=〈o
,≫〉,P
[2]=(p
,p
);γ
[3]=〈p
,≫〉,P
[3]=(p
,p
);γ
[3]=〈m
,≫〉,P
[3]=(p
,p
);γ
[3]=〈o
,≫〉,P
[3]=(p
,p
);γ
[4]=〈n
,≫〉,P
[4]=(p
,p
);继而执行第六步,观察所有保留的日志移动对,如果不同对齐中有相同的日志移动,则取它们对应库所的交集,若交集为空集,则无需变动。此步骤执行结果为:P
[1]=P
[4]=(p
);P
[2]=P
[3]=(p
);P
[2]=P
[3]=(p
);P
[3]=(p
,p
);最后执行第七步,整理保留下来的库所集,得到一个日志移动的可修复库所集P
={P
[1]=P
[4]=(p
);P
[2]=P
[3]=(p
);P
[2]=P
[3]=(p
);P
[3]=(p
,p
)}.
(2)物流派送流程模型修复及验证分析
找到日志移动的可修复库所集,便可根据“插入和跳过活动”的方法和基于子流程的修复算法对模型进行修复。通过观察,日志移动〈p
,≫〉是单个日志移动,且不同对齐中没有与之相同的日志移动,因此,修复模型时只需在库所p
或p
上插入活动事件p
即可,修复结果如图2所示。对于日志移动〈m
,≫〉,〈o
,≫〉是连续的日志移动,而且不同对齐中有相同的日志移动,对应库所交集为p
,这与日志移动〈n
,≫〉所对应库所一致,因此,同时在同一个库所上插入三个活动事件,需要考虑这三个事件是否具有某种行为关系,通过分析日志可知,活动事件m
,o
的每次执行都是同时出现且具有一定的顺序关系,而且并没有与活动事件n
同时出现过,因此,判断活动事件m
,o
是严格序关系,且与活动事件n
是排他序关系。因此通过它们之间的行为轮廓关系,构建一个子流程,如图3所示,然后将子流程按照基于子流程的模型修复算法,插入到模型中的p
上。故最终修复模型如图4所示。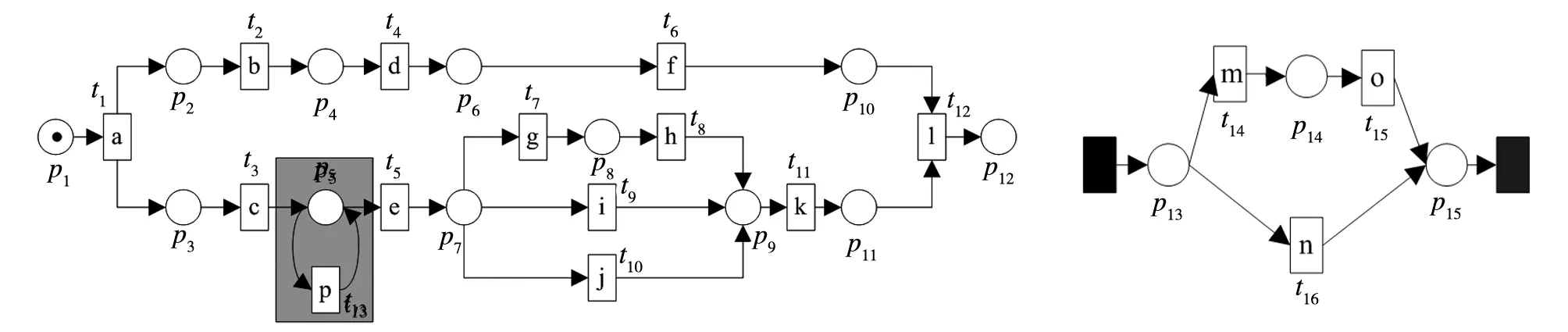
图2 插入活动事件p的修复模型N1 图3 根据行为轮廓关系构建的子流程

图4 最终修复模型N′
为了验证修复模型的合理性,计算了修复模型与日志的适合度。其中适合度公式如下
fitness(L
,M
)=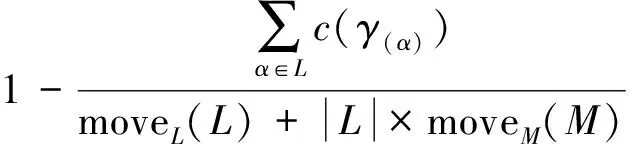
(1)
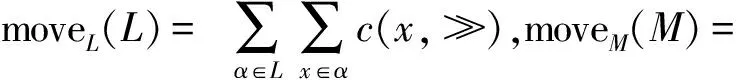
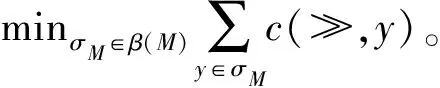
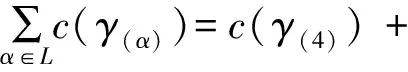
c
(γ
)+c
(γ
)+c
(γ
)=0,因此fitness(L
,M
)=1-0=1。从而说明了事件日志与修复模型完全拟合。4 结论
本文主要基于Petri网构建了一个物流派送的流程模型,并对事件日志与流程模型进行了一致性检查及模型修复分析。首先,本文根据给定事件日志构建一个流程模型。其次,主要基于成本对齐的方法,根据其成本大小判断事件日志与流程模型之间的偏差大小。在对偏差部分进行模型修复过程中,本文给出了寻找日志移动的可修复库所集的算法,该算法有助于实现模型修复。最后,根据基于子流程的模型修复方法以及行为轮廓关系对模型进行修复,使得流程模型能够完全重放事件日志,并最大可能地与原始模型相似。通过计算得到日志与模型间的适合度为1,从而也说明修复模型具有合理性。
未来工作中,将致力于在修复模型适合度为1的情况下尽可能提高其精确度,并使得修复模型具有普遍适用性。

