基于多元统计与Bayes判别模型的水源判别

李 凌，胡友彪，刘 瑜，琚棋定

(1.安徽理工大学地球与环境学院，安徽 淮南 232001；2.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001)

矿井突水是影响煤矿安全生产的重要因素之一，我国煤矿生产中突水事故频发，矿井水害的发生不仅会造成巨大的经济损失，而且可能会造成人员伤亡。一旦发生煤矿突水事故，及时准确地判断突水水源，查明突水原因，是治理和预防矿井水害的关键。根据井田内含水层的水化学特征，可以发现相应含水层的内在联系，因此众多专家学者围绕含水层水样的水化学特征对矿井突水水源判别方面展开研究。文献[5]等通过水化学特征分析与灰色关联判别相结合的方法建立矿井突水水源识别模型，在定性和定量分析的基础上判别良庄煤矿51101工作面突水水源。文献[6]等通过因子分析和距离判别相结合的方法来判断矿井突水，为矿井水害防治提供理论基础。文献[7]等基于水化学和矩阵方程分析，分别建立了矿井突水的模糊综合评判方法和矩阵方程分析模型。文献[8]等采用基于主成分分析建立的PCA-GRA突水水源判别模型识别不同矿井的突水水源。用水化学成分判别突水水源具有准确、快速、经济的特点，其他根据矿井水样的水化学特征进行突水水源判别的方法还有基于Logistic回归分析方法、聚类分析法、Fisher判别法、PCA-FDA、可拓判别法、BP神经网络、同位素法等。

以往建立的单一Bayes判别函数，并没有对水化学参数进行处理，也忽略了含水层离子之间的内在联系，导致判别效果不理想。本文以袁店一矿为例，提出了一种基于多元统计分析和Bayes判别法结合的矿井突水水源判别方法，先利用因子分析和系统聚类分析对水样水化学数据进行处理，再结合Bayes判别法建立矿井突水水源判别模型。通过与单一Bayes判别法相比，本文方法能够更加有效判别矿井突水水源。

1 研究区概况

袁店一矿位于淮北煤田临涣矿区的南部，构造特征总体上为走向北北西，倾向北东的单斜断块，发育有波幅较小的次级小褶曲，走向上地层线表现为波浪状。研究区所在区域的主要含水层有新生界松散层“四含”水(四含水)、二叠系砂岩裂隙水(砂岩水)、太原组灰岩岩溶裂隙水(太灰水)、奥陶系灰岩岩溶裂隙水(奥灰水)。

生产实践证明,四含直接覆盖在煤系地层之上，岩性泥质含量高，渗透性差及补给条件较差，富水性弱，是矿井充水的主要补给水源之一，但一般补给量不大。煤系砂岩含水层富水性较弱，地下水处于封闭～半封闭环境，补给条件差，以静储量为主，且具有衰减疏干的趋势。含水层以砂岩为主，其中主采煤层顶底板砂岩裂隙水是煤矿生产过程中矿井直接充水水源。太原组灰岩含水层岩溶裂隙发育具有不均一性，灰岩岩溶裂隙在浅部较发育，向深部逐渐减弱，是10煤安全开采的主要隐患之一。由于奥灰水远离主采煤层，一般对煤层开采无直接充水影响。

2 矿井水源识别的多元统计分析

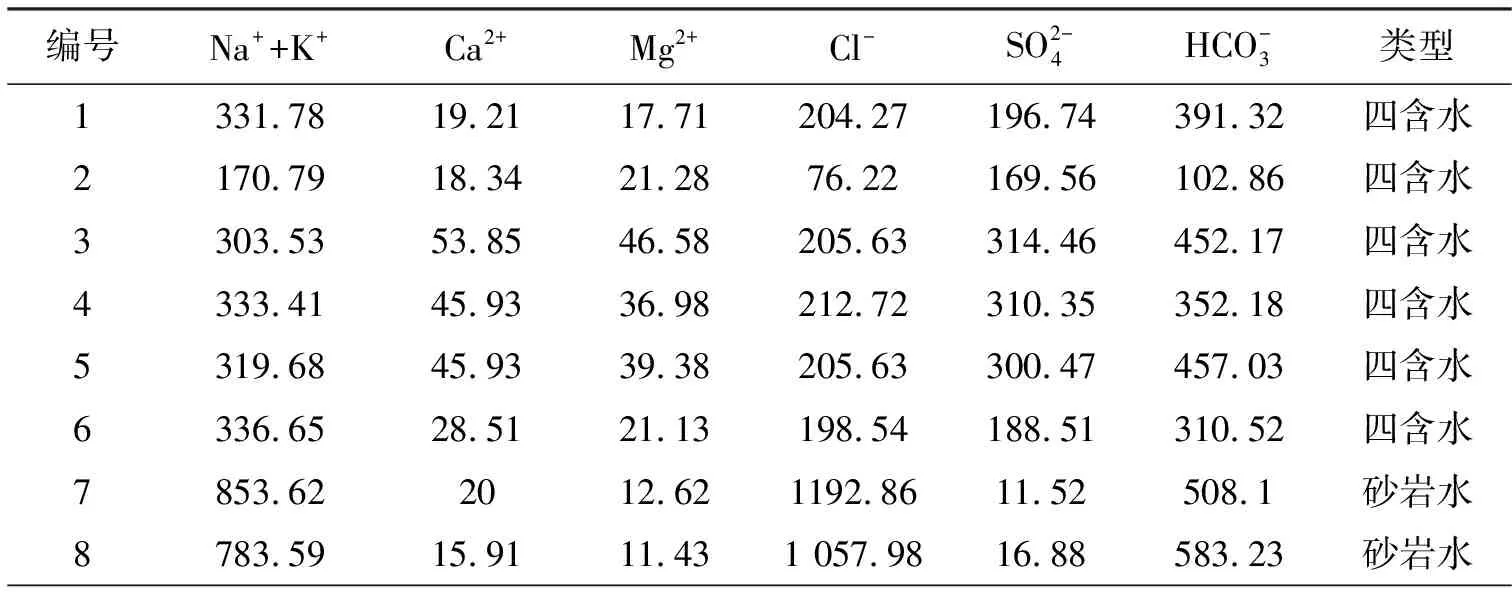
表1 袁店一矿地下水化学特征 mg·L-1

编号Na++K+Ca2+Mg2+Cl-SO2-4HCO-3类型9544.982013.081 966.755.15783.41砂岩水10786.4413.138.23565.1943.63928.94砂岩水11987.058.362.661 143.679.88651.54砂岩水12859.9012.8210.661 136.687.41411.79砂岩水13593.1419.3914.151 392.734.12340.41砂岩水14943.4416.114.151 306.237374.36砂岩水15481.227.54.74223.9925.11312.42砂岩水16387.0411.3612.24309.1781.96705.44砂岩水17414.6713.025.23408.3432.93673.01砂岩水18340.989.194.18206.1118.52537.52砂岩水191135.4420.6216.321 058.84.53468.98砂岩水20735.4921.5412.58932.1521.4455.45砂岩水21807.3923.1314.511 094.1212.88407.76砂岩水221 188.6426.5920.521 596.8217408.79砂岩水23382.7915.544.32271.2231.91376.22砂岩水24343.9213.568.71210.9525.11495.14砂岩水25308.9626.635.8386.1381.09600.39砂岩水26486.735.7715.48193.2236.65531.02砂岩水27346.6134.39.67203.8565.87509.49砂岩水28471.414.3610.16196.7625.52379.67砂岩水29343.9213.568.71310.9525.11495.14砂岩水30232.5159.0234.34230.07299.23434.17太灰水31119.4269.8410.9217.369.97466.19太灰水32134.0965.118.1935.4575.32244.07太灰水33127.4988.0853.45217.9965.44372.47太灰水34537.1262.2935.51196.47181.93437.03太灰水35267.1716.3614.51113.5258.04511.81太灰水36143.2431.3934.3544.04103.72399.64太灰水37324.39109.8483.31145.55685.31288.29太灰水

(1)因子分析

主成分分析与因子分析的基本思路是在多个原始变量中利用它们之间的内部相关性，通过降维分析获得新的变量(主成分变量或因子变量)，达到既能减少分析指标个数，又能概括原始数据主要信息的目的。其中主成分分析是将原来多个相互联系的变量通过线性组合方式降维压缩成几个少数综合变量去包含原数据尽可能多的信息，但是得到的综合变量往往不具有明显的现实意义。因子分析在包含原数据信息量方面有优势，而且利用尽可能少的因子来反映样本信息，所以通过线性组合提取的公因子比主成分分析提取的主成分更具有解释性。因子分析是研究多个变量间的相互联系，找出综合所有变量主要信息的几个综合指标(通常称为因子)，所有变量都可以表示成无相关性的公因子的线性组合。通过下面的数学模型来实现

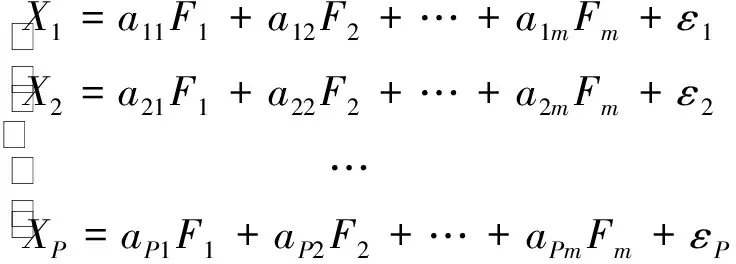
(1)

式中：

X

、

X

…

X

为样本的

p

个指标，

F

、

F

…

F

，为

m

个因子变量，

m

<

p

。矩阵形式如下=+

ε

(2)

式中：=(

a

)为因子载荷矩阵，

a

为因子载荷，表示因子变量，

ε

为特殊因子(实际分析时忽略不计)。利用Matlab对上述6类离子进行相关性分析，得出离子间的相关系数(见表2)。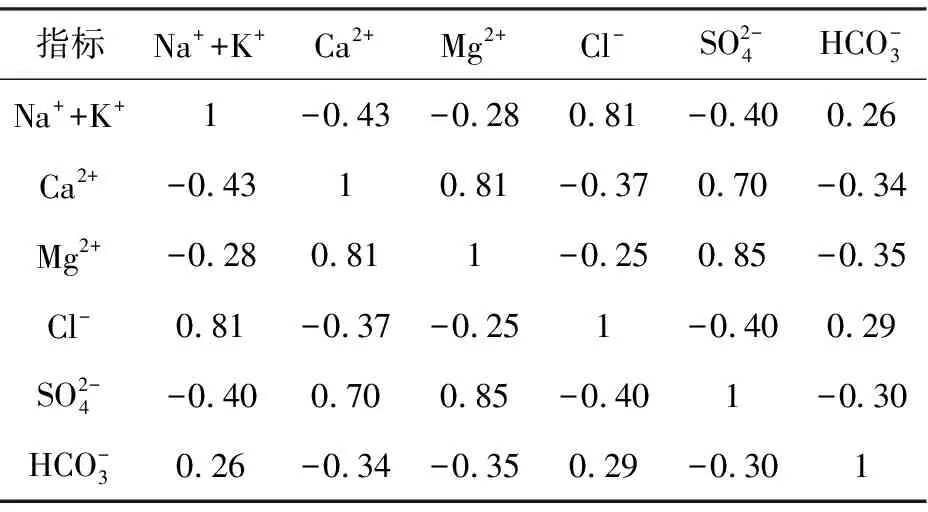

表2 水化学指标相关系数矩阵

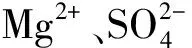
运用Matlab软件中的因子分析对数据进行处理，提取初始因子得到6类离子变量的初始因子特征值和解释后的特征值(见表3)以及PCA分析图(见图1)。

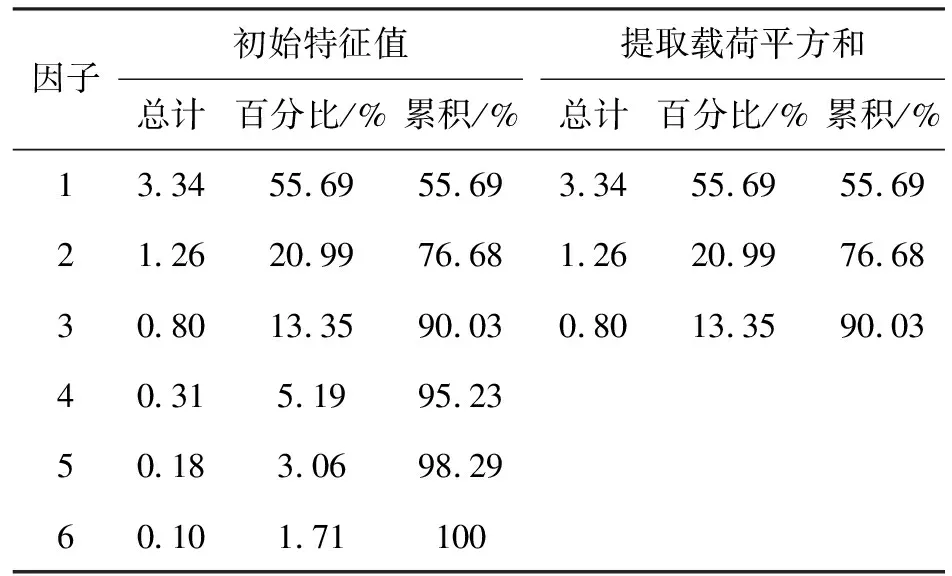
表3 总方差解释

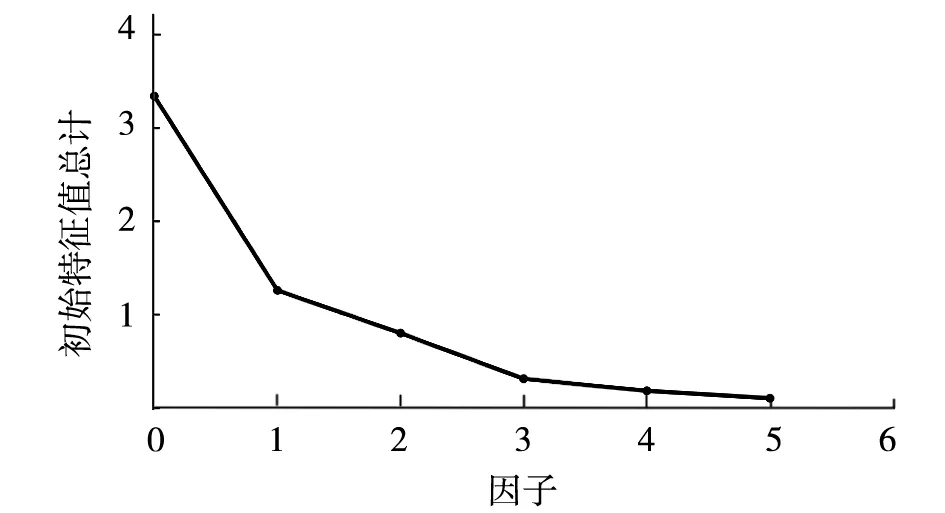
图1 PCA分析图

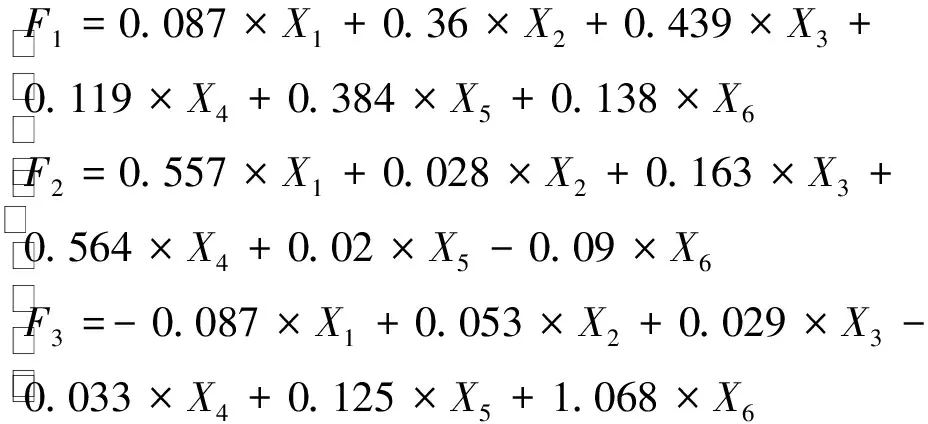
(3)

式中：

X

～

X

为离子浓度。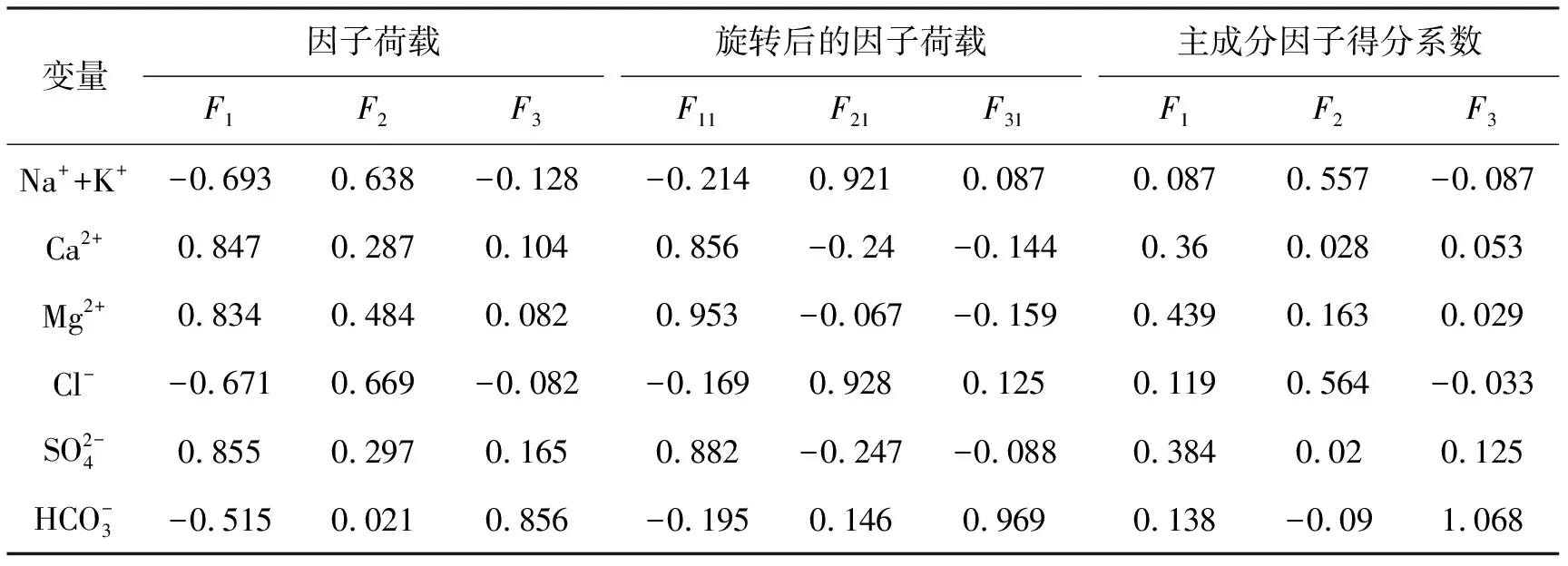

表4 因子荷载矩阵

(2)因子得分系统聚类分析

系统聚类分析法的基本思想是先计算样品之间的距离或类与类之间的距离，把相似性质(或距离最近)的样品划归为一类，再重新计算该类与当前各类之间的距离，按照最小距离归类，直至所有样品归为一类为止。由于矿井水样的采取点没有明显的规律，用聚类分析的方法，结合统计水样的相似度作为校对标准，把相似度高的水样作为一类，这样大致可以认为同类型水样所在取样点位置的地下水具有相似的水化学特征。由数据生成的聚类分析谱系图可以更加清楚地看出各个水样的相似性和特征。

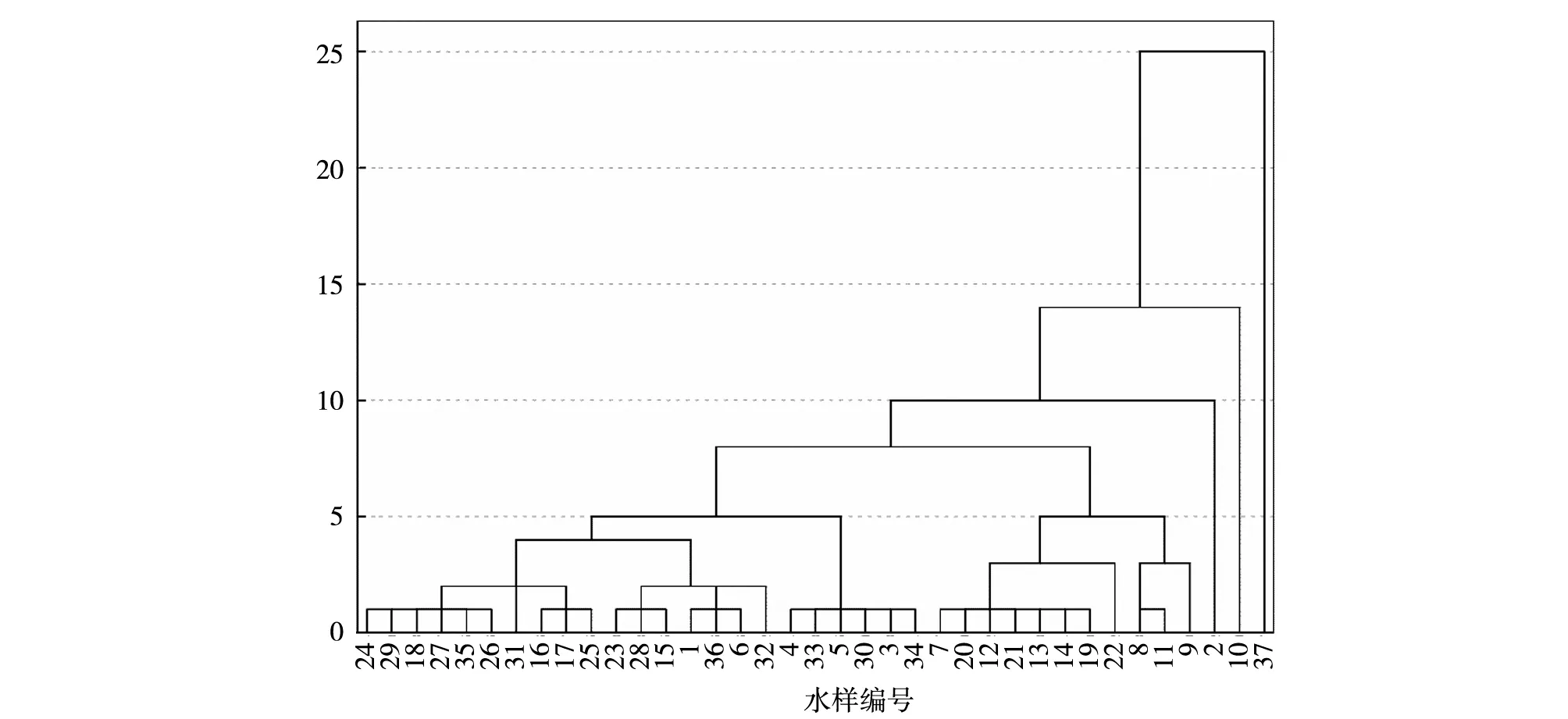
图2 系统聚类谱系图

本文中利用Matlab软件中的组间平均连接法和平方欧式距离作为度量标准，以37个水样的因子得分作为变量进行Q型系统聚类，根据因子得分系统聚类谱系图(见图2)，确定因子得分之间的相关性。其中各水样因子得分通过表达式(3)计算得到(见表5)。从聚类谱系图中根据水样间的相关性，将错误水样2、10、34、35、36、37号剔除，从图中也可以看出四含水、砂岩水和太灰水之间存在一定的联系，部分水样可以归为一类，说明各含水层之间存在着水力联系。

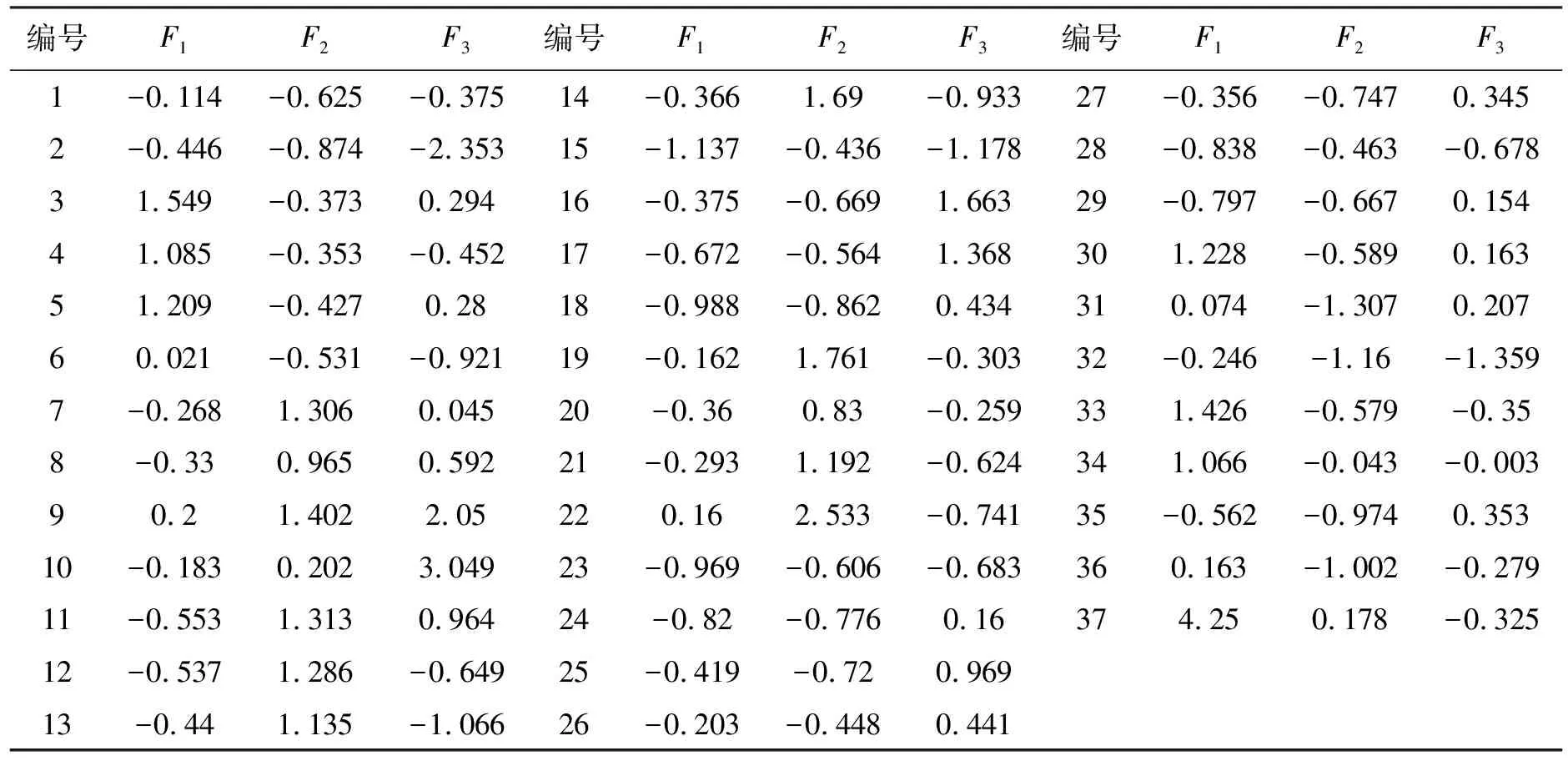
表5 因子得分

3 突水水源判别与分析

(1)Bayes判别函数模型的建立

Bayes判别法是以最大后验概率法和错分概率最小为判别规则。通过求出各含水层的Bayes判别函数来进行水样的类型判别。利用上述因子分析法得到的水样主成分因子得分，再结合聚类分析法剔除6个错误水样，用剩余的31个水样通过Matlab软件建立三种水样的Bayes判别函数：

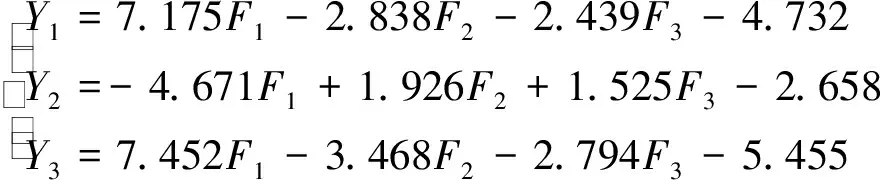
(4)

式中：

Y

、

Y

、

Y

分别表示四含水、砂岩水以及太灰水的判别函数；

F

F

、

F

表示提取能代表样本信息的因子。

根据Bayes最大后验概率规则，将主因子得分代入3种判别式中，得到的函数值最大的类型即为水样所属类型。

若不采用因子分析与聚类分析时的单一Bayes判别函数为：

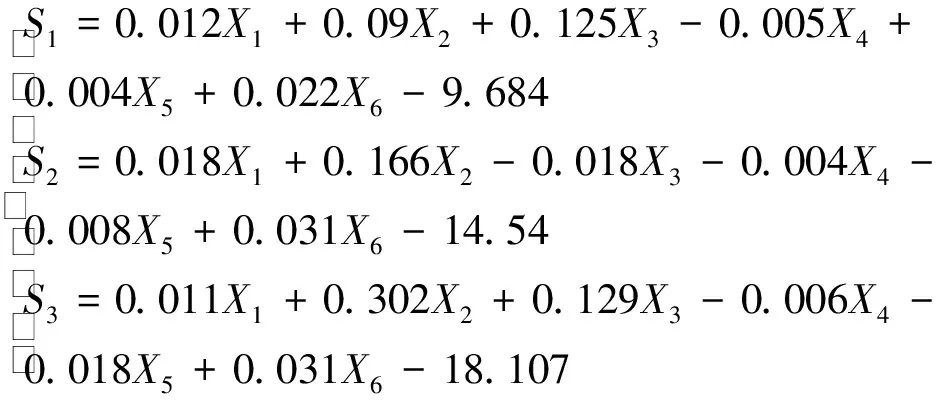
(5)

式中：

S

、

S

、

S

分别表示四含水、砂岩水以及太灰水的判别函数。

(2)判别效果检验

将剔除错误水样后的31组训练样本因子得分回代到建立的Bayes判别函数中，按最大后验概率法进行归类(见表6)。从表中可知，运用多元统计分析建立的Bayes判别函数对四含水和煤系砂岩水的识别正确率达到了100%，对太灰水样的识别也仅出现了一个错误，总体识别准确率为96.7%；相比未经任何处理直接建立的Bayes判别结果(见表7)显示：1组四含水误判为太灰水，1组砂岩水误判为四含水，3组太灰水误判为四含水，准确率为88.6%。由此可见，本文建立的判别模型能够更有效识别突水水源类型，且对太灰水的判别效果更好。

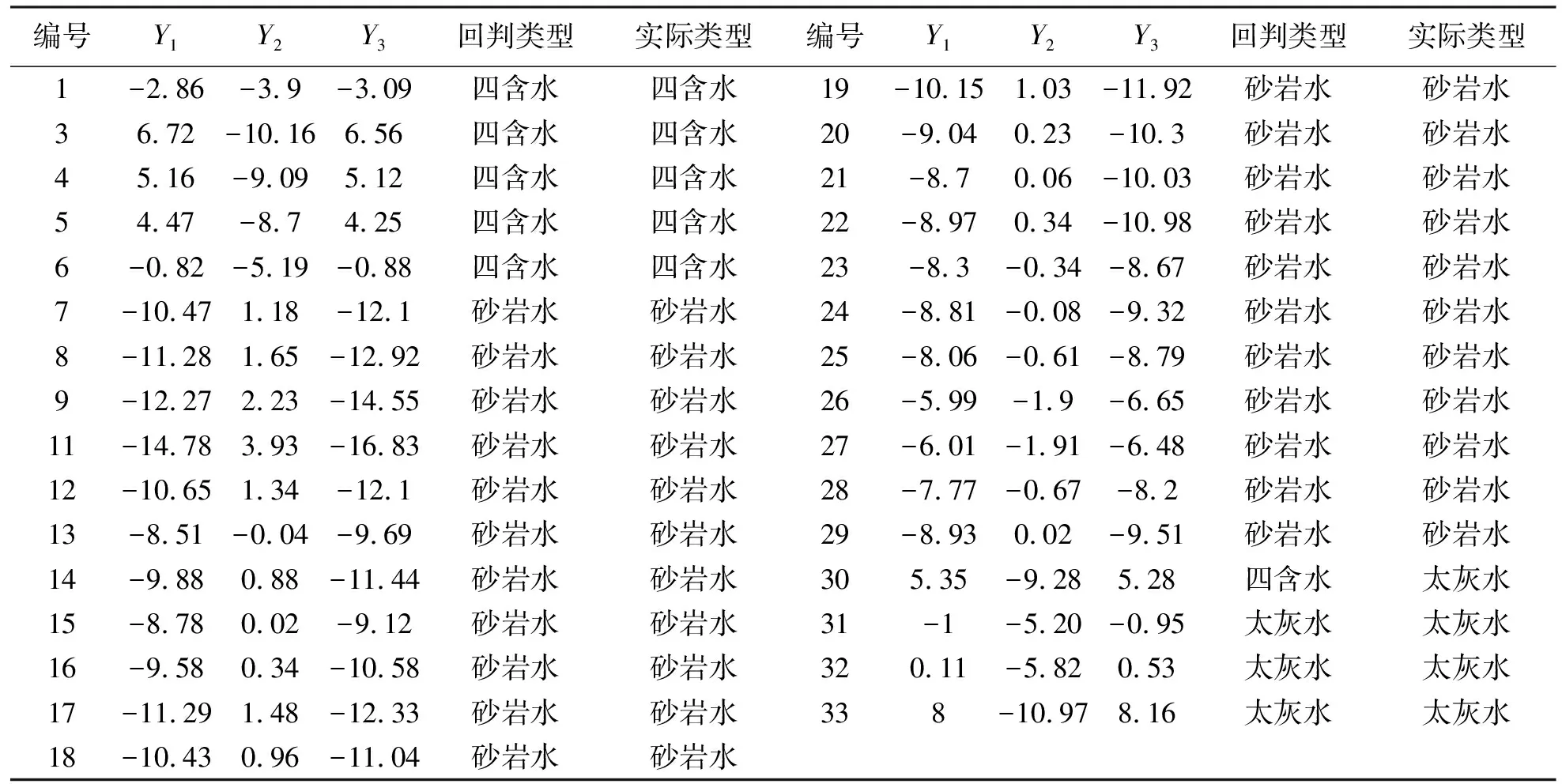
表6 回判结果

表7 单一Bayes判别结果

(3)判别模型的应用与分析

运用本文方法建立的判别模型和不作任何处理的单一Bayes判别模型，以袁店一井收集的剩余的7组水样作为预测水样类型进行判别，对比结果如表8所示。由表8可知，单一Bayes判别模型对太灰水的判别出现一个错误，证明了运用本文方法对太灰水样的判别效果有明显提升。

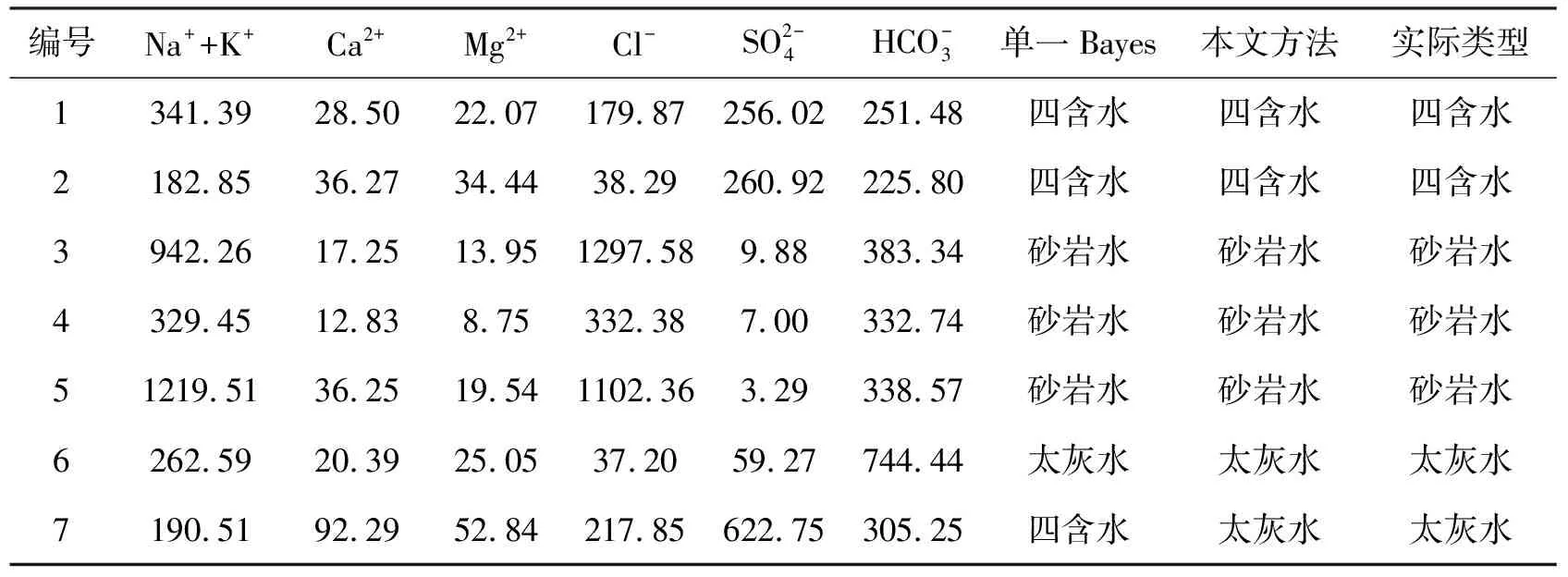
表8 预测水样判别对比结果 mg·L-1

4 结论

(1)以淮北袁店一矿水化学资料为基础，运用因子分析法与聚类分析法相结合，预先对水样离子数据进行综合分析，再利用剔除错误水样后的因子得分建立Bayes判别模型，其判别准确率可达96.7%。

(2)运用两种多元统计分析方法对Bayes判别模型进行定量化处理，将水样离子质量浓度代入判别模型中即可准确判别水样类型。与单一Bayes判别模型相比，能有效提高结果的准确性。