软土地区地铁环境振动对精密仪器的影响研究

（中铁工程设计咨询集团有限公司，北京 100055）

1 引言

城市轨道交通具有运量大、速度快、安全性好、准点率高等诸多优点，但地铁运营中出现了沿线工厂、科研机构内精密仪器运行受影响，以及周边建筑结构内二次噪声超标等环境振动问题。

软土地区含水率大、压缩性高、剪切波速小，地铁列车动力作用对周边环境振动影响大，且在中低频范围内振动增加明显。因此，环境振动对精密仪器的影响愈发引起人们的重视，诸多专家学者针对这一问题进行了大量测试与研究，包括北京地铁4号线列车运行引起的振动对北京大学物理楼内精密仪器的影响，北京地铁16号线规划通过北京大学西门对200 m外的实验楼内精密仪器的影响，北京地铁15号线规划下穿清华大学对校内200余台精密仪器的影响，北京地铁10号线近距离经过中国空间技术研究院等。以上工程案例均存在环境振动对精密仪器的影响问题，且难以解决。目前降低环境振动对精密仪器的影响措施主要为被动隔振措施，但效果十分有限，故研究地铁线路周边精密仪器合理的放置距离十分必要。

苏州地铁6号线苏州大学站—徐家浜站区段邻近苏州大学某实验楼，实验楼中多台精密仪器受到地铁振动的影响。苏州地铁6号线位于软土地区，由其导致的周边建筑结构振动及其衰减特性尚不明确，需对苏州地铁6号线对该建筑（实验楼）内精密仪器的影响程度进行模拟计算评估。

2 环境振动分析预测有限元模型

本文结合苏州地铁6号线苏州大学站—徐家浜站区段减振轨道工程案例，基于有限元方法建立包含车辆、轨道、隧道、土体、建筑的动力学有限元模型。苏州地铁6号线采用地铁B型车，列车运行速度60 km/h，钢弹簧浮置板轨道板长6 m，钢弹簧与扣件采用弹簧单元模拟，轨道结构如图1所示。

有限元模型中轨面至地表距离20 m，在模型中分别考虑隧道中心线距建筑物（内有精密仪器）20 m、50 m、100 m 3种工况。模型隧道为单洞单线隧道，隧道直径6 m，纵向长96 m。隧道衬砌为C50混凝土。建筑物为钢混结构，共4层（含地下一层），建筑物梁、柱、墙、板均采用C30混凝土，建筑物与周围土体共结点绑定。地铁隧道-建筑物空间位置关系如图2所示。

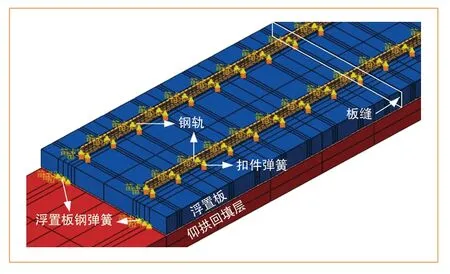
图1 轨道结构示意图

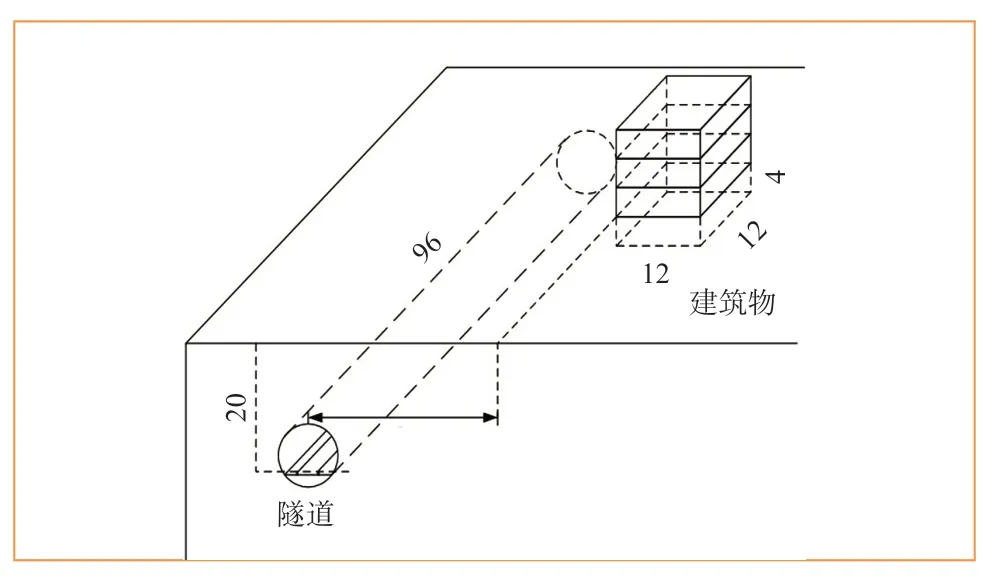
图2 隧道-建筑物空间位置关系示意图（单位：m）

研究表明交通荷载引起的土体动应变在10-5以下，在仿真中可忽略土体的塑性变形；有限元分析中，将隧道和土层之间的连接按照共用节点的方式处理，土体结构采用实体单元模拟，参数根据地勘报告取值。

本文采用三维黏弹性人工边界作为边界条件，以减少边界反射带来的影响。三维黏弹性人工边界的等效物理系统的切向、法向弹簧系数和切向、法向阻尼系数分别为

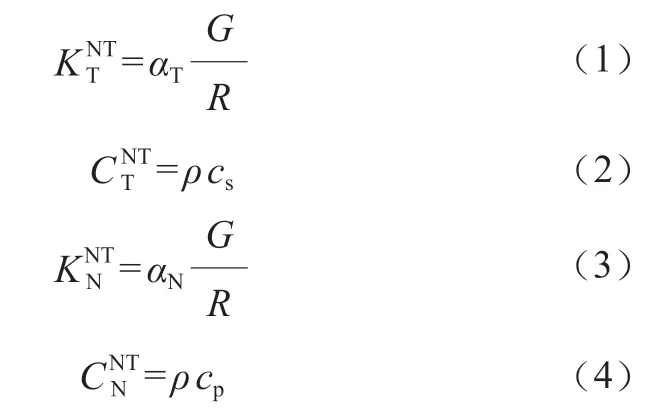
式（1）～式（4）中，R为振源与人工边界间的距离；G为介质剪切模量；ρ为土体密度；cs为剪切波速；cp为压缩波速；αT和αN分别为切向和法向黏弹性人工边界参数，其取值范围分别为0.5～1.0和1.0～2.0，结合文献[18]，本文取αT=0.67，αN=1.33。

图3 环境振动分析预测模型

本文应用ABAQUS显式算法，建立环境振动分析预测模型如图3所示，模型共包含1 386 000个网格单元，采用美国六级谱作为轮轨激励。

3 浮置板振动模态分析

振动模态是弹性结构固有的、整体的特性，了解结构的固有属性是进行结构振动特性分析的重要前提。当外界激励频率与结构模态相近时，结构的振动响应将显著增大。本文基于有限元软件ABAQUS线性摄动分析，采用子空间迭代法分析进行钢弹簧浮置板模态分析，得到的钢弹簧浮置板典型模态频率如图4所示，其中前2阶4.86 Hz与12.58 Hz模态为浮置板纵向上的转动，此为浮置短板的特征模态，亦为钢弹簧浮置板主要的运动模态，其后为1阶弯曲，再之后为复杂的扭转与高阶弯曲模态。由此可知，钢弹簧浮置板的主要模态频率较低，在外界荷载激励作用下，钢弹簧浮置板将难以隔绝低频振动。

4 动力学仿真分析

4.1 轨道-隧道结构动力响应

为分析振源位置的振动响应特性，选取钢轨、轨道板、隧道壁（高1.2 m处）位置上各1点进行振动加速度时程与振动加速度1/3倍频程分析，所得结果如图 5、图6所示。由图5可知，钢轨峰值加速度为120 m/s2，轨道板峰值加速度为13 m/s2，隧道壁振动加速度峰值为0.05 m/s2；由图6可知，在12.5 Hz附近出现明显的峰值，分析原因与浮置板主要的运动模态相关。

4.2 地面自由场振动衰减分析

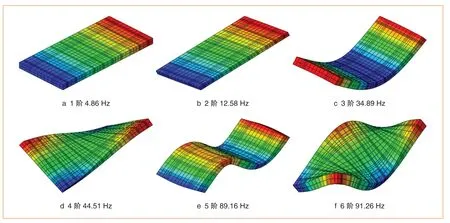
图4 钢弹簧浮置板典型模态频率

图5 钢轨、轨道板、隧道壁振动加速度时程曲线

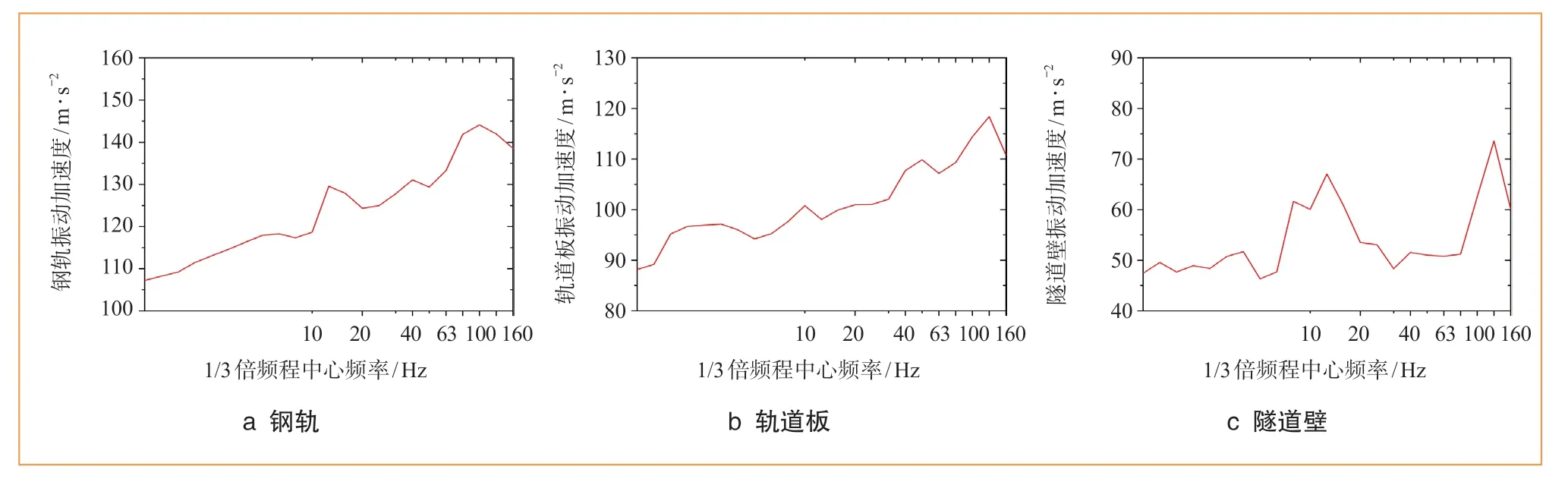
图6 钢轨、轨道板、隧道壁振动加速度1/3倍频程曲线

为研究列车运行振动引起地表自由场振动衰减规律，在距隧道中心线0～115 m的范围内选取了一些典型测点，并选择对远场影响较大的垂向振动加速度作为研究指标，计算得到距隧道中心线不同距离与垂向振动加速度关系曲线如图7所示。由图7可知，在15 m左右出现明显的“振动放大区”，该位置至隧道中心线的距离与地铁隧道埋深相近；在80～90 m附近出现第2个放大区；随着距离的增加，整体上振动加速度呈减小趋势，最大振动加速度位于距隧道中心线15 m左右位置。

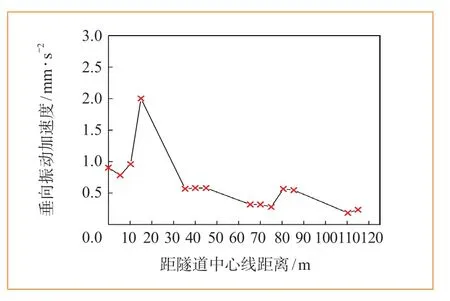
图7 地表垂向振动加速度与隧道中心线距离关系曲线

5 建筑结构室内振动响应与影响评估

本文工程实例中，实验楼内放置有需要满足VC标准（Generic Vibration Criteria）中VC-D级振动标准的精密仪器。VC标准制定的目的是给出特定工艺和设备振动标准的下限，VC标准以1组1/3倍频带速度谱的形式标记振动标准曲线（VC-A到VC-G），VC-D级标准要求速度均方根值小于6.25 μm/s。计算得到的不同楼层、不同振源距离位置处的速度均方值1/3倍频程曲线如图8、图9所示（图中红线表示VC-D振动标准限值），由图8可知，所有位置速度均方值1/3倍频程关系曲线均在4 Hz、12.5 Hz处存在速度均方根值峰值，对比分析图8、图9不同振源距离、不同楼层速度均方值1/3倍频程曲线可知，距振源20 m、50 m的建筑物内的振动速度均方值均超过精密仪器对环境振动的要求限值，距振源100 m的建筑物内仍有环境振动超限的风险。

6 结论及建议

本文通过建立软土地区环境振动分析预测模型，对苏州大学某实验楼受苏州地铁6号线环境振动影响问题进行分析计算，得到主要结论如下：

（1）地铁环境振动对精密仪器的影响频率范围主要是12.5 Hz左右的低频振动；

（2）地铁环境振动在自由场地的传播中存在部分“振动放大区”，本文中在距隧道中心线100 m的计算范围内，存在15 m和80 m 2个较为明显的振动放大区；

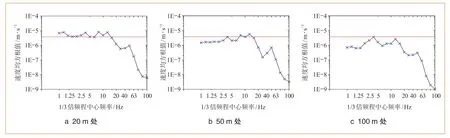
图8 负一层地板速度均方值1/3倍频程曲线

图9 地面地板速度均方值1/3倍频程曲线

（3）本文中距振源20 m、50 m、100 m 3种工况中，距振源20 m、50 m的建筑物内振动超过精密仪器对环境振动的要求限值，距振源100 m的建筑物内仍有振动超限的风险；

（4）软土地区距离地铁线路100 m的范围内不应放置精密仪器。